Year 11 Algebraic Fractions Worksheets
What are algebraic fractions and why do students find them challenging?
Algebraic fractions are fractions where the numerator, denominator, or both contain algebraic expressions rather than just numbers. At GCSE level, students need to simplify, add, subtract, multiply, and divide these expressions, treating them with the same rules that apply to numerical fractions but requiring additional factorisation and algebraic manipulation skills. This topic sits at the intersection of fractions knowledge and algebra fluency, making it a reliable indicator of whether students have truly mastered both areas.
The challenge arises because students must hold multiple processes in mind simultaneously. When subtracting algebraic fractions, for instance, many students correctly find a common denominator but then forget to multiply the entire numerator by the scaling factor, particularly when that numerator contains more than one term. Mark schemes regularly penalise students who write (x+3)/2x - x/4x = (x+3-x)/4x instead of (2x+6-x)/4x, losing method marks even if their subsequent simplification is correct. Students who methodically bracket numerators before combining fractions avoid this trap.
Which year groups study algebraic fractions?
Algebraic fractions appear in the Year 11 curriculum as part of Key Stage 4, typically introduced after students have developed confidence with factorising quadratic expressions and manipulating complex algebraic terms. The National Curriculum requires students to simplify, add, subtract, multiply, and divide algebraic fractions, with the expectation that Higher tier students can handle increasingly complex expressions involving quadratic numerators and denominators. This topic usually features in the spring term of Year 11 as part of final GCSE preparation.
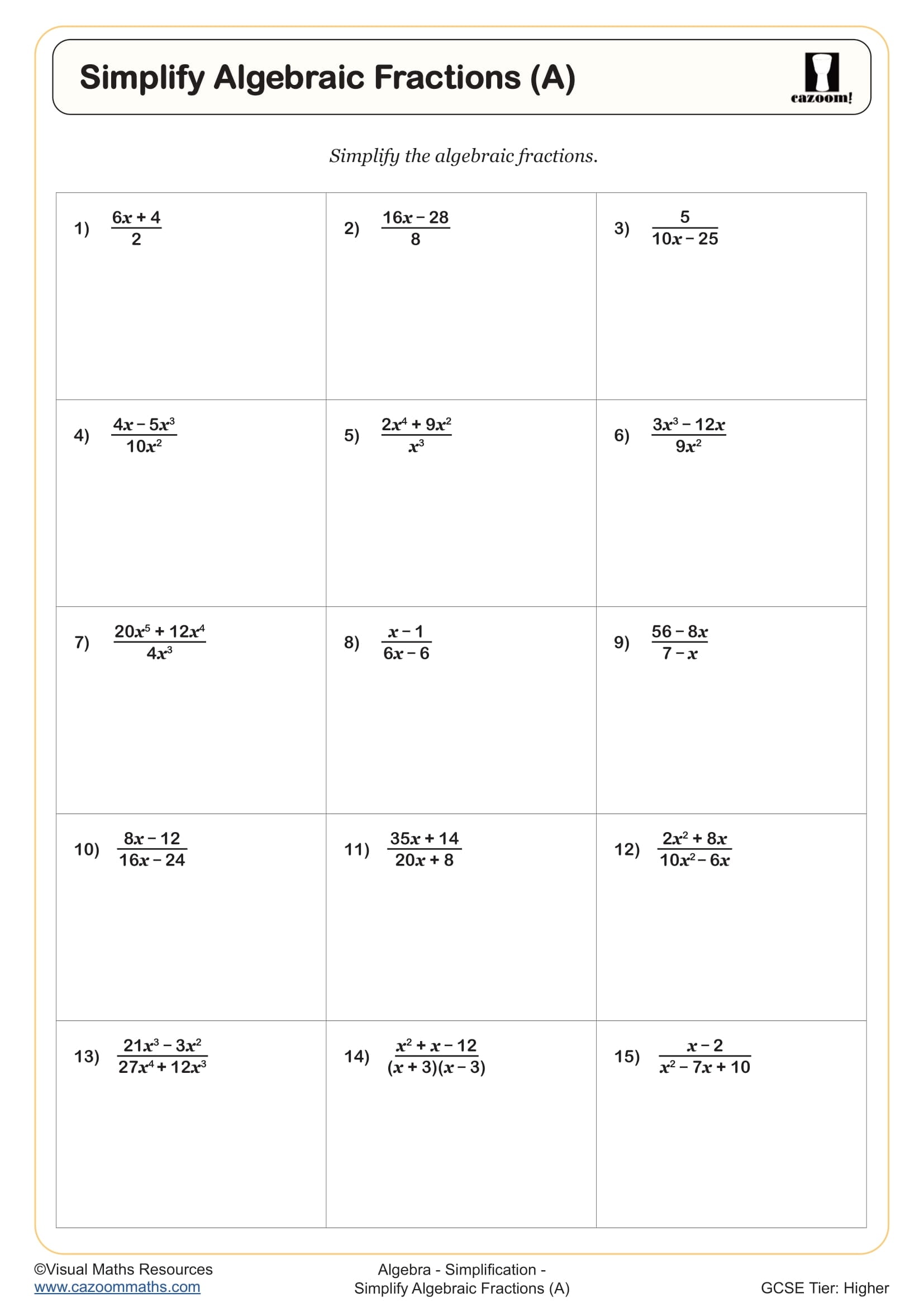
While basic simplification of single algebraic fractions may be touched upon in Year 10, the systematic study of operations with algebraic fractions, particularly subtraction and division, consolidates in Year 11. Teachers often revisit this topic during Easter revision because exam questions frequently combine algebraic fractions with equations or inequalities. Foundation students encounter simpler versions (such as simplifying x²/2x or combining fractions with matching denominators), whilst Higher students face multi-step problems requiring factorisation of quadratics before cancelling and complex common denominators involving binomial expressions.
How does dividing algebraic fractions connect to other maths topics?
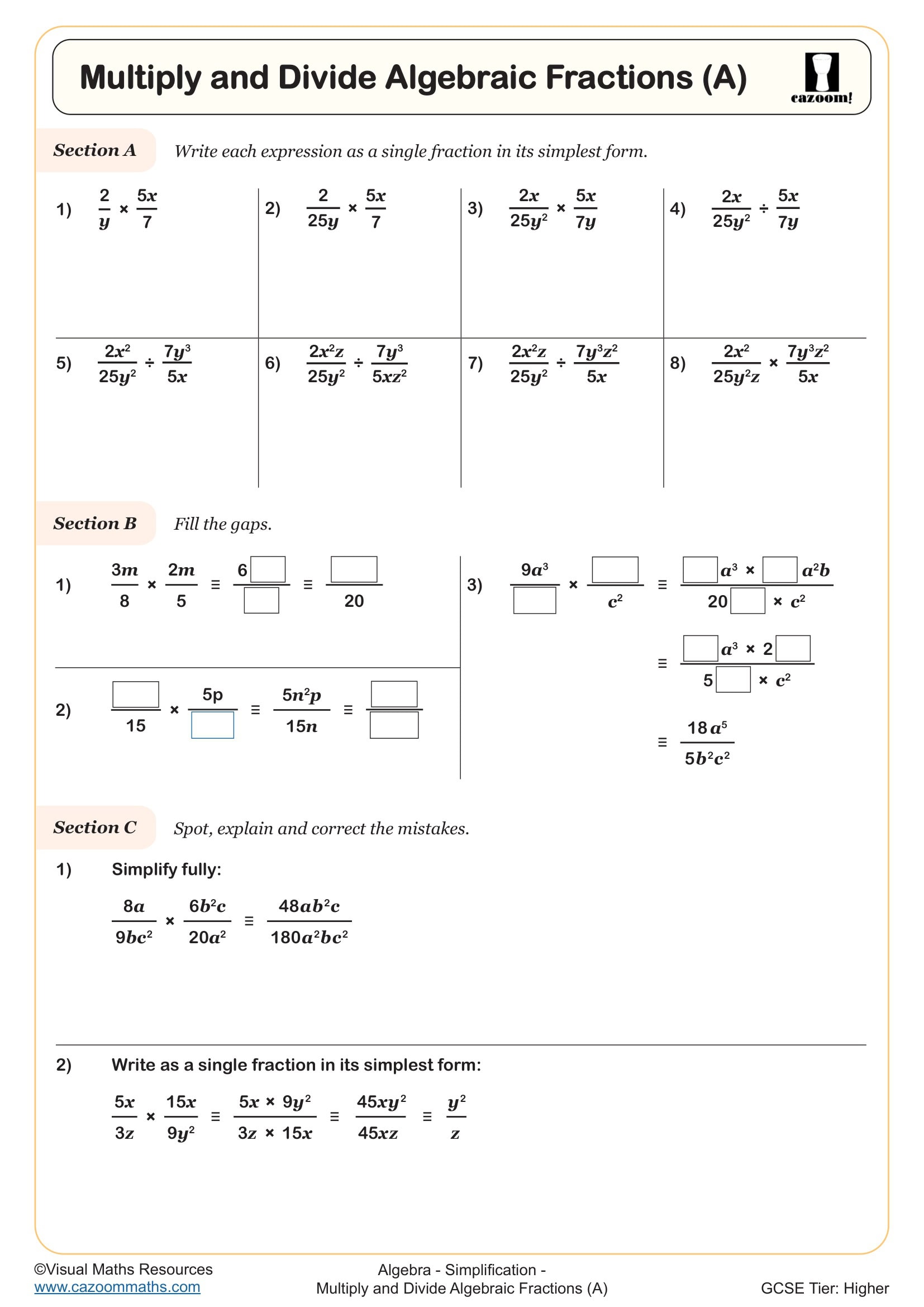
Dividing algebraic fractions follows the same principle as dividing numerical fractions: multiply by the reciprocal of the divisor. Students rewrite division problems such as (2x/3) ÷ (x²/6) as (2x/3) × (6/x²), then multiply numerators together and denominators together before simplifying. The crucial skill here is recognising common factors that cancel across the fraction bar, which requires confident factorisation. Students who attempt to divide without flipping the second fraction or who try to 'cancel across the division sign' produce incorrect solutions that lose all marks in examinations.
This operation appears frequently in physics calculations involving rates and proportional relationships. When students rearrange formulae like speed = distance/time to find time = distance/speed, they're performing division of expressions that may themselves be fractions. In engineering contexts, calculating gear ratios or mechanical advantage involves dividing one fractional relationship by another. Understanding that dividing by a fraction means multiplying by its reciprocal helps students make sense of why a smaller gear can produce greater rotational force, connecting abstract algebraic manipulation to physical systems.
How can these worksheets support students preparing for GCSE exams?
The worksheets break down operations with algebraic fractions into manageable steps, with questions progressing from straightforward simplification through to multi-step problems that mirror exam-style questions. Each worksheet targets specific skills, whether that's dividing expressions, subtracting fractions with different denominators, or combining multiple operations in one question. The answer sheets allow students to identify exactly where their method breaks down, whether it's an error in finding common denominators, incorrect factorisation, or a sign mistake when expanding brackets.
These resources work effectively for targeted intervention with small groups who've struggled with this topic in mock exams, as well as for homework following initial teaching. Teachers often use one worksheet as guided practice immediately after direct instruction, then assign a second for independent consolidation. During revision periods, students can work through the collection at their own pace, using the answers to self-assess and highlight specific techniques that need revisiting. Paired work can be particularly valuable here, with one student explaining their method whilst their partner checks each step against the answer sheet, encouraging mathematical discussion about where errors typically occur.