Menu

PRIMARYSECONDARYGCSE REVISION
SCHOOLSSEARCH
LOGINFREE TRIAL

Year 11 Area Model Worksheets

These Year 11 area model worksheets help students visualise algebraic multiplication and factorisation through a structured geometric approach. The area model breaks down expressions into manageable sections, making complex operations like expanding double brackets or factorising quadratics more accessible. Teachers frequently notice that students who struggle with abstract algebraic manipulation often gain clarity when they can see how terms combine within the rectangular grid structure. This visual representation particularly supports understanding of why like terms appear when multiplying out brackets. Each worksheet downloads as a PDF with complete answer sheets included, allowing students to check their working independently and identify where errors occur in their calculations.

Completing the Square - Using Algebra Tiles

Completing the Square - Using Algebra Tiles Worksheet created for students in KS4

Expanding Double Brackets with Surds - Using the Grid Method

Expanding Double Brackets with Surds - Using the Grid Method worksheet

Expanding Triple Brackets (A)

Expanding Triple Brackets Worksheet created for students in KS4

Factorising Quadratic Expressions - Using the Area Model (A)

Factorising Quadratic Expressions - Using the Area Model (A) worksheet

Factorising Quadratic Expressions - Using the Area Model (B)

Factorising Quadratic Expressions - Using the Area Model (B) worksheet

All worksheets are created by the team of experienced teachers at Cazoom Maths.

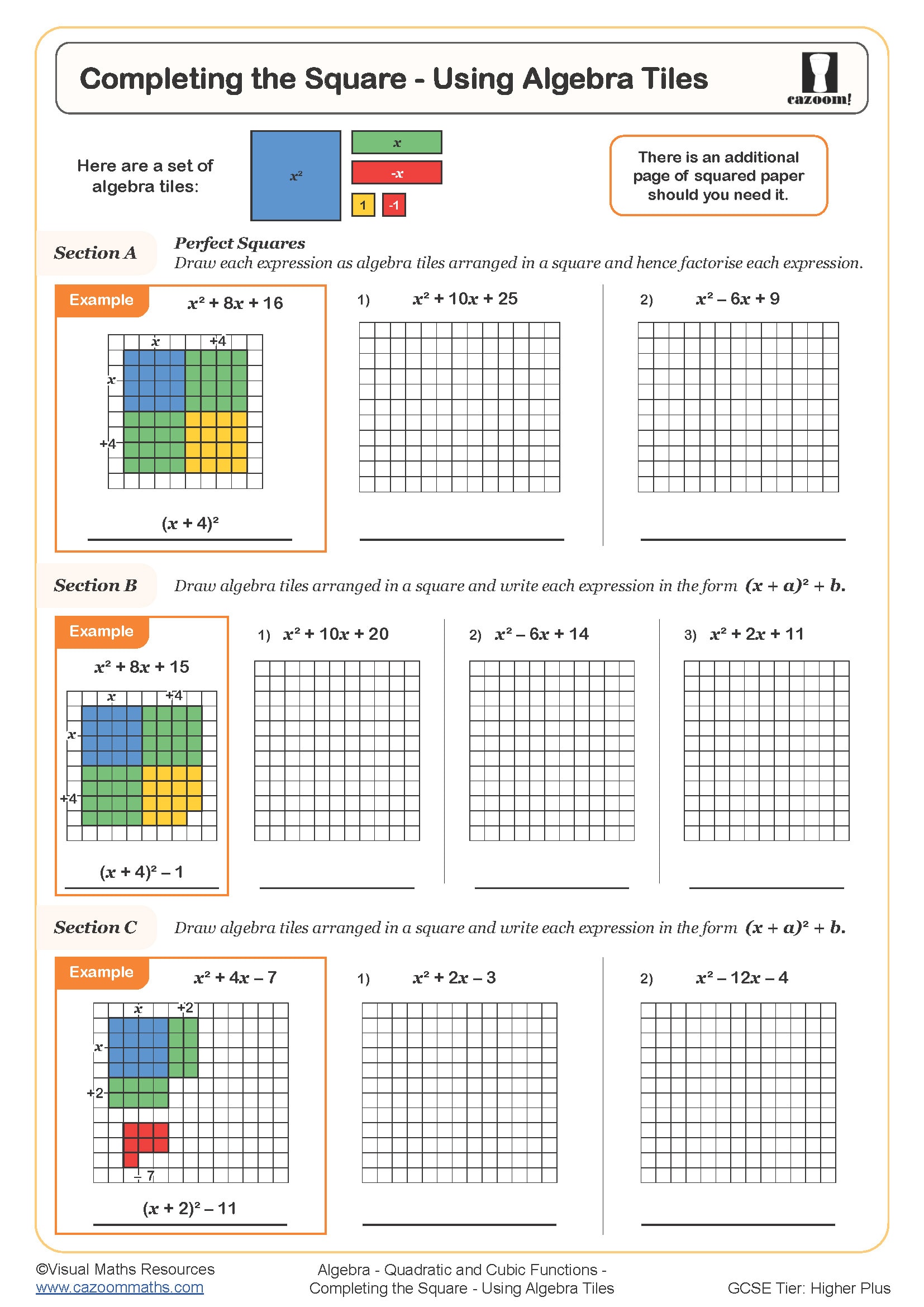
What is the area model method in maths?

The area model is a visual method for multiplying algebraic expressions by representing them as the dimensions of a rectangle, then calculating the area of each section. Students divide a rectangle into smaller sections based on the terms being multiplied, fill each section with the product of its row and column headers, then combine all sections to find the total expression. This approach appears across KS3 and KS4, supporting both numerical multiplication and algebraic work.

A common error occurs when students correctly fill in the area model grid but then fail to simplify their final answer by collecting like terms. For example, when expanding (x + 3)(x + 5), students might write x² + 5x + 3x + 15 but forget to combine the middle terms to get x² + 8x + 15. Exam mark schemes expect the simplified form, and students lose marks when they leave expressions uncollected.

Which year groups use area model worksheets?

These area model worksheets target Year 11 students at KS4 level, where the method supports GCSE preparation for algebraic manipulation questions. At this stage, students apply the area model to expand and factorise quadratic expressions, work with binomial products, and solve equations that require manipulation of more complex algebraic forms. The technique reinforces understanding needed for both Foundation and Higher tier papers.

By Year 11, students should be moving beyond basic single-bracket expansion to confidently handle double brackets and recognise when factorisation is required. The area model provides a reliable checking method even when students can perform algebraic multiplication mentally, offering a visual verification tool during exam revision that reduces careless errors with signs and coefficients.

How does the area model help with factorising quadratics?

Factorising with the area model works in reverse: students start with the expanded quadratic expression and determine which terms form the length and width of the rectangle. They place the x² term and constant in opposite corners, then identify two numbers that multiply to give the constant term while their sum (or difference) produces the coefficient of x. This visual structure helps students see the relationship between factors and expanded forms more clearly than algebraic manipulation alone.

This skill connects directly to engineering and physics applications where quadratic relationships describe motion, area calculations, and optimisation problems. When engineers design rectangular enclosures with fixed perimeters, they use factorised quadratics to determine dimensions that maximise area. Understanding the geometric basis through area models helps students recognise why quadratic functions appear in real-world contexts involving two-dimensional measurements and relationships.

How can teachers use these area model worksheets effectively?

The worksheets build systematically from straightforward binomial products to more challenging quadratic expressions, allowing teachers to select appropriate starting points based on individual student confidence. Each question type repeats with different numbers, giving students sufficient practice to internalise the grid structure before moving to purely symbolic methods. The included answer sheets mean students can work independently during consolidation phases while teachers circulate to address specific misconceptions.

Many teachers use these resources during intervention sessions with students who find abstract algebra particularly challenging, as the visual approach often unlocks understanding where symbolic methods have failed. The worksheets also work well for homework following initial teaching, allowing students to practise the method with fresh examples. During revision periods, paired work where one student completes the area model while their partner uses traditional algebraic expansion helps both students verify their approaches and spot errors in their reasoning.