Year 11 Bearings Scale and Loci Worksheets
What are the common mistakes students make with bearings and loci?
The most frequent error involves measuring bearings anticlockwise rather than clockwise from north, particularly when finding back bearings where students often subtract from 360° incorrectly. Teachers regularly see students write bearings as two-digit numbers (85° instead of 085°) or measure from the wrong reference line when multiple bearings appear on the same diagram. With loci, students typically draw arcs too faintly or fail to leave construction lines visible, which costs marks even when the final answer is correct.
Another common issue occurs when scale questions involve mixed units. Students might correctly measure a distance as 8 cm but forget to convert using the scale, or they apply the scale in the wrong direction. Exam mark schemes specifically require construction arcs and working to be shown, yet many students erase these thinking they're making their work neater, losing valuable method marks in the process.
Which year groups study bearings, scale and loci?
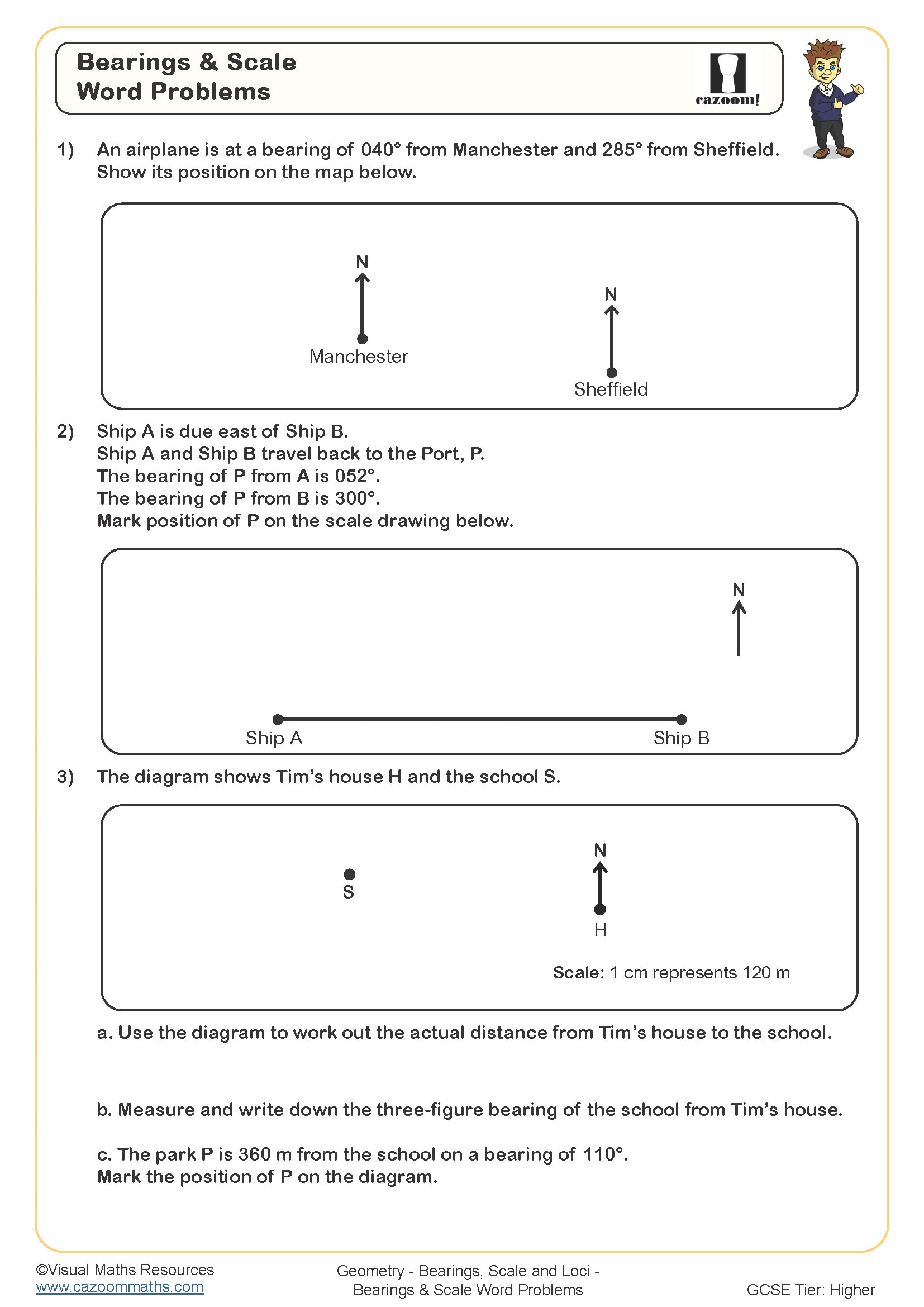
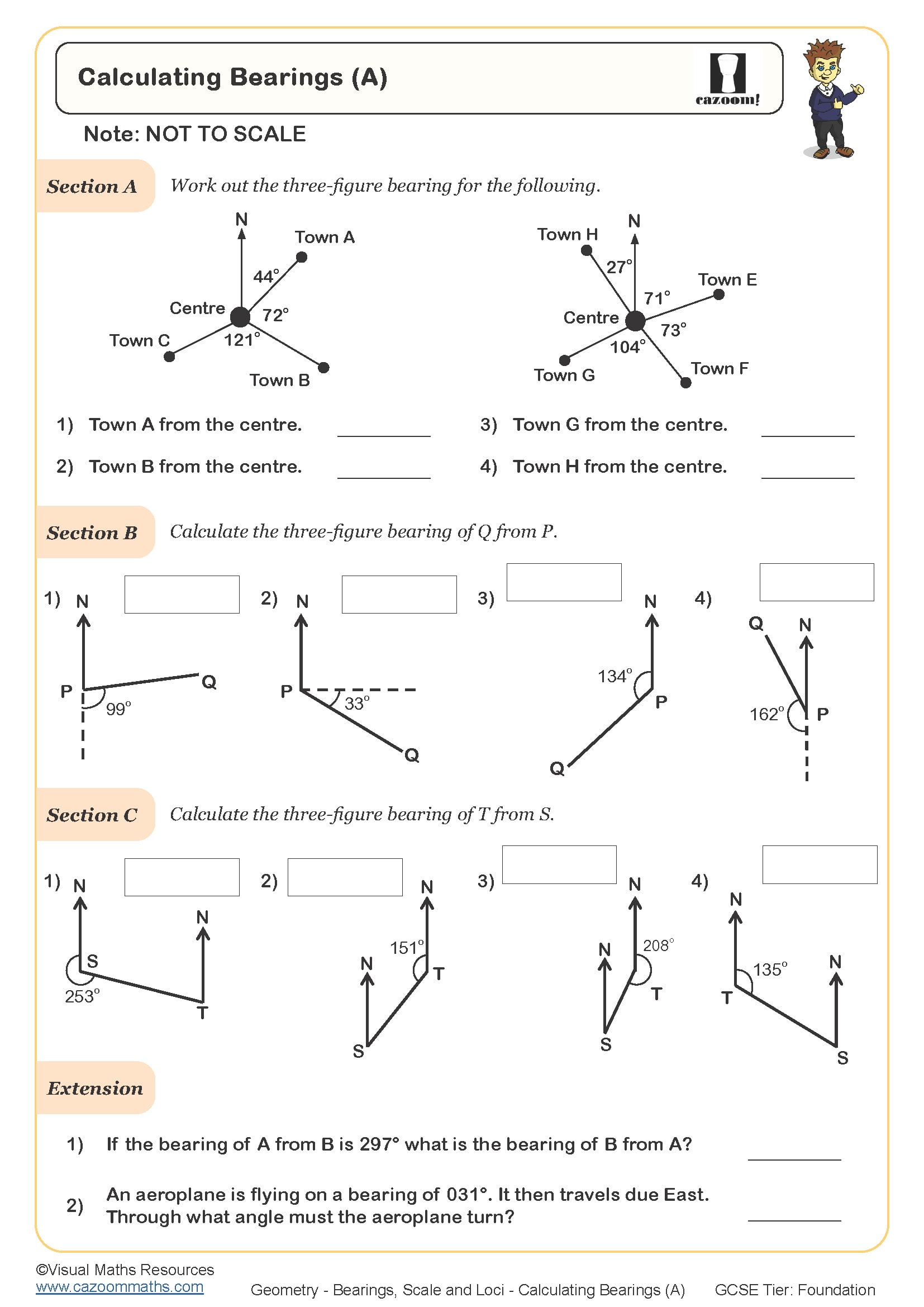
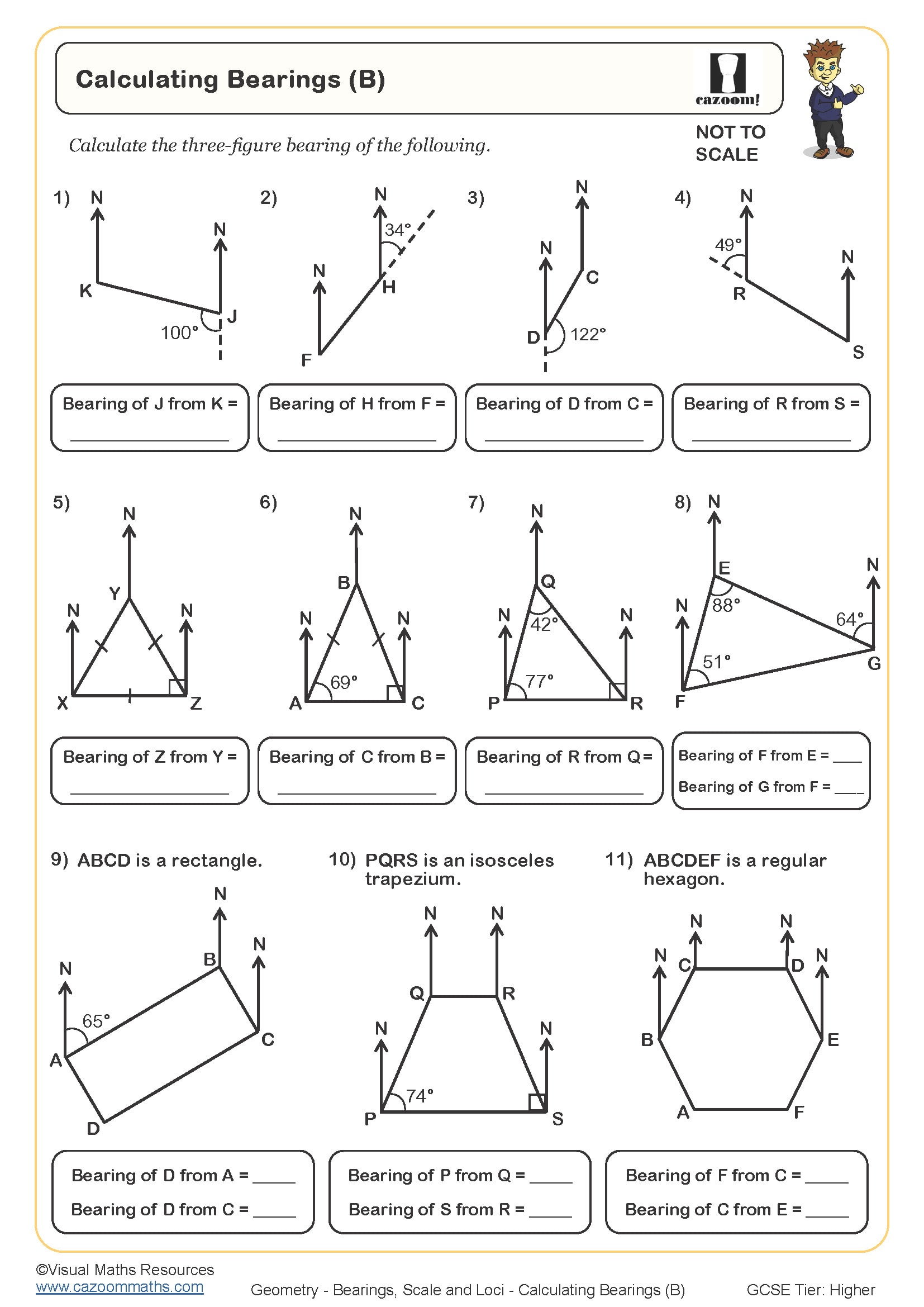
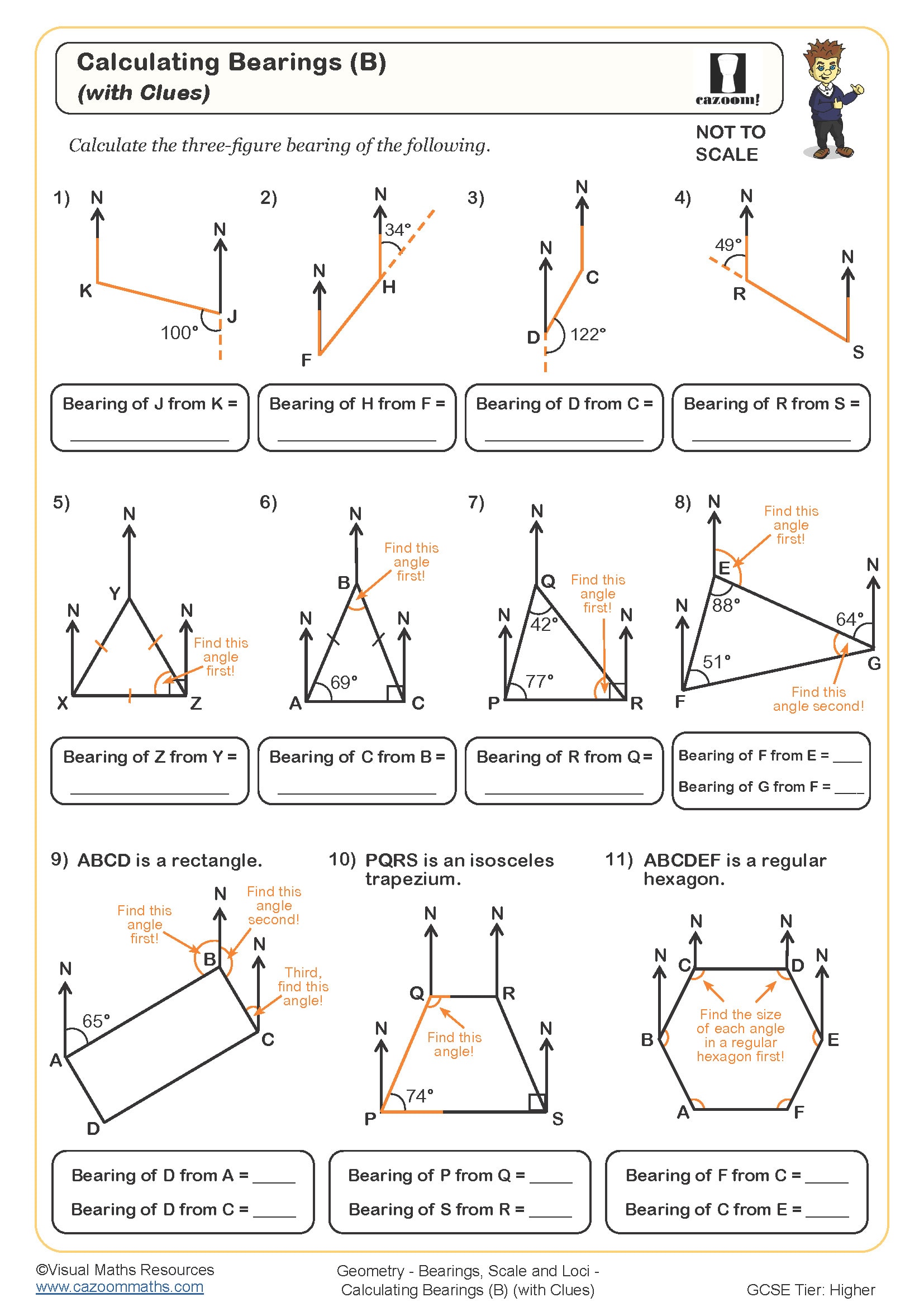
This topic appears in Year 11 as students prepare for GCSE Foundation and Higher tier examinations. At KS4, bearings typically appear alongside scale drawings and loci because exam questions frequently combine these skills within navigation, construction or design contexts. Students are expected to measure and draw bearings accurately to the nearest degree, construct loci using compasses and rulers, and work confidently with scales expressed as ratios or in the form 1 cm represents a given distance.
Whilst students might encounter basic scale work in Years 7-9, the integration of bearings with compound loci problems represents a significant step up in complexity. Foundation tier questions tend to involve straightforward single bearings or one-stage loci, whereas Higher tier papers may require students to find regions satisfying multiple conditions or calculate distances using both scale and bearings within the same multi-step problem.
How are loci used in real-world applications?
A locus represents the set of all points satisfying a particular condition, which students construct using compasses and a ruler. Common constructions include the perpendicular bisector of a line segment, the bisector of an angle, points equidistant from a fixed point (circles), and points equidistant from a line (parallel lines). Exam questions often ask students to shade regions satisfying two or three conditions simultaneously, requiring careful construction and accurate identification of where loci intersect.
Civil engineers use loci principles when planning mobile phone mast coverage or determining safe zones around hazardous sites, where regions must satisfy multiple distance constraints. Architects apply these concepts when positioning buildings to maximise sunlight whilst maintaining required distances from boundaries. In telecommunications, determining signal coverage areas involves constructing circles of specific radii, whilst emergency service planning uses bearings and loci together to identify optimal locations for stations that can reach incidents within target response times.
How do these worksheets help students prepare for GCSE questions?
The worksheets build skills progressively, starting with isolated practice on measuring and drawing three-figure bearings before introducing back bearings and more complex diagrams. Scale drawing questions begin with straightforward conversions before progressing to problems where students must both measure from diagrams and create their own scaled representations. Loci questions develop from single constructions to compound problems where students identify regions satisfying multiple conditions, mirroring the structure of actual exam questions.
Teachers often use these worksheets during intervention sessions with students who struggle to visualise spatial problems or need repeated practice with compass constructions. The answer sheets make them effective for homework tasks where students can self-check their accuracy, particularly important for constructions where small errors compound. Many teachers find them valuable for paired work, where one student measures bearings or distances whilst their partner checks accuracy against the answer sheet, building both technical skill and the ability to verify geometric constructions systematically.