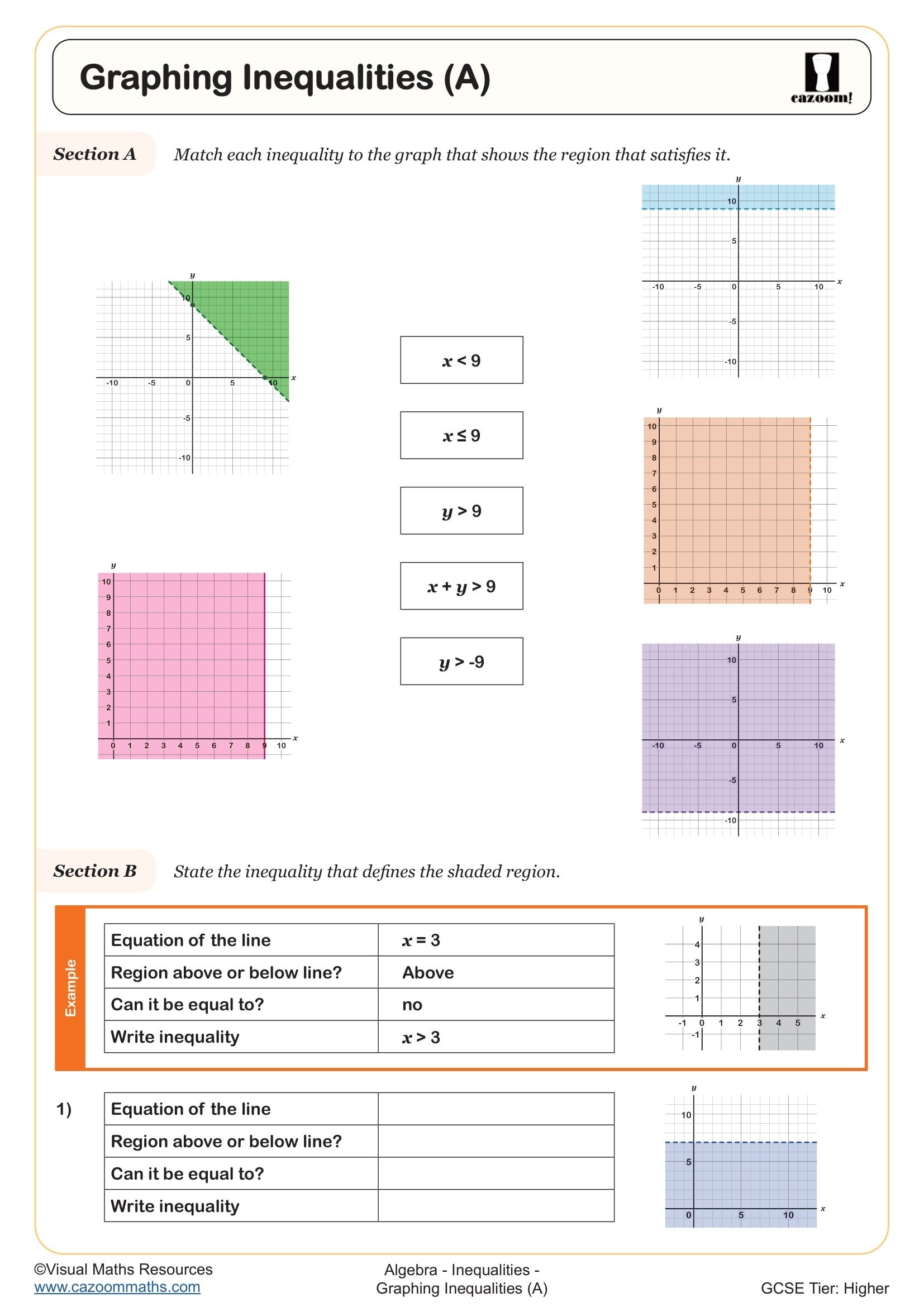
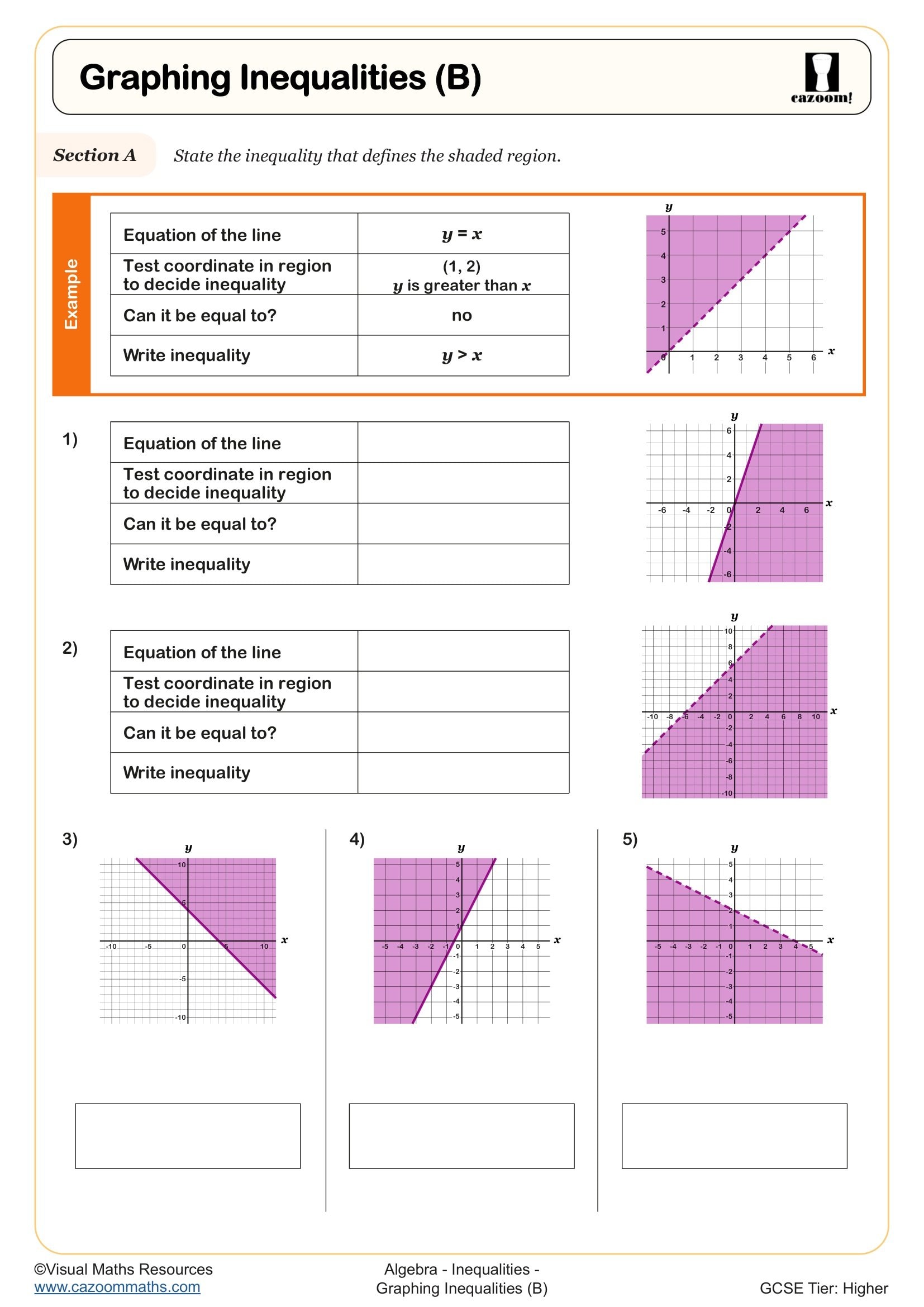
Year 11 Inequalities Worksheets
-Worksheet.jpg)
-without-sketching-Questions.jpg)
-satisfying-two-inequalities-Worksheet.jpg?w=3840)
What common mistakes do students make when solving linear inequalities?
The most persistent error when solving linear inequalities involves the treatment of negative coefficients. Students routinely forget to flip the inequality sign when multiplying or dividing both sides by a negative number, writing x > 3 instead of x < 3. This misconception stems from over-applying equation-solving procedures without recognising that inequalities behave differently. Exam mark schemes specifically penalise this error, and it appears across Foundation and Higher tier papers.
Another frequent mistake occurs when students reach an answer like -x < 4 and simply write the solution as x < -4 without recognising they need to divide by -1 (and therefore reverse the sign) to get x > -4. Teachers observe that students who regularly practise identifying when sign reversal is needed develop more reliable checking habits, often substituting a value from their solution back into the original inequality to verify their answer makes sense.
Which year groups study inequalities?
These worksheets target Year 11 students preparing for GCSE examinations, where inequalities feature prominently in both Foundation and Higher tier papers. At KS4, students are expected to solve linear inequalities in one variable, represent solutions on number lines, and work with compound inequalities involving two conditions. This builds directly on the foundation work from Year 9 and Year 10, where students first encounter inequality notation and basic solution methods.
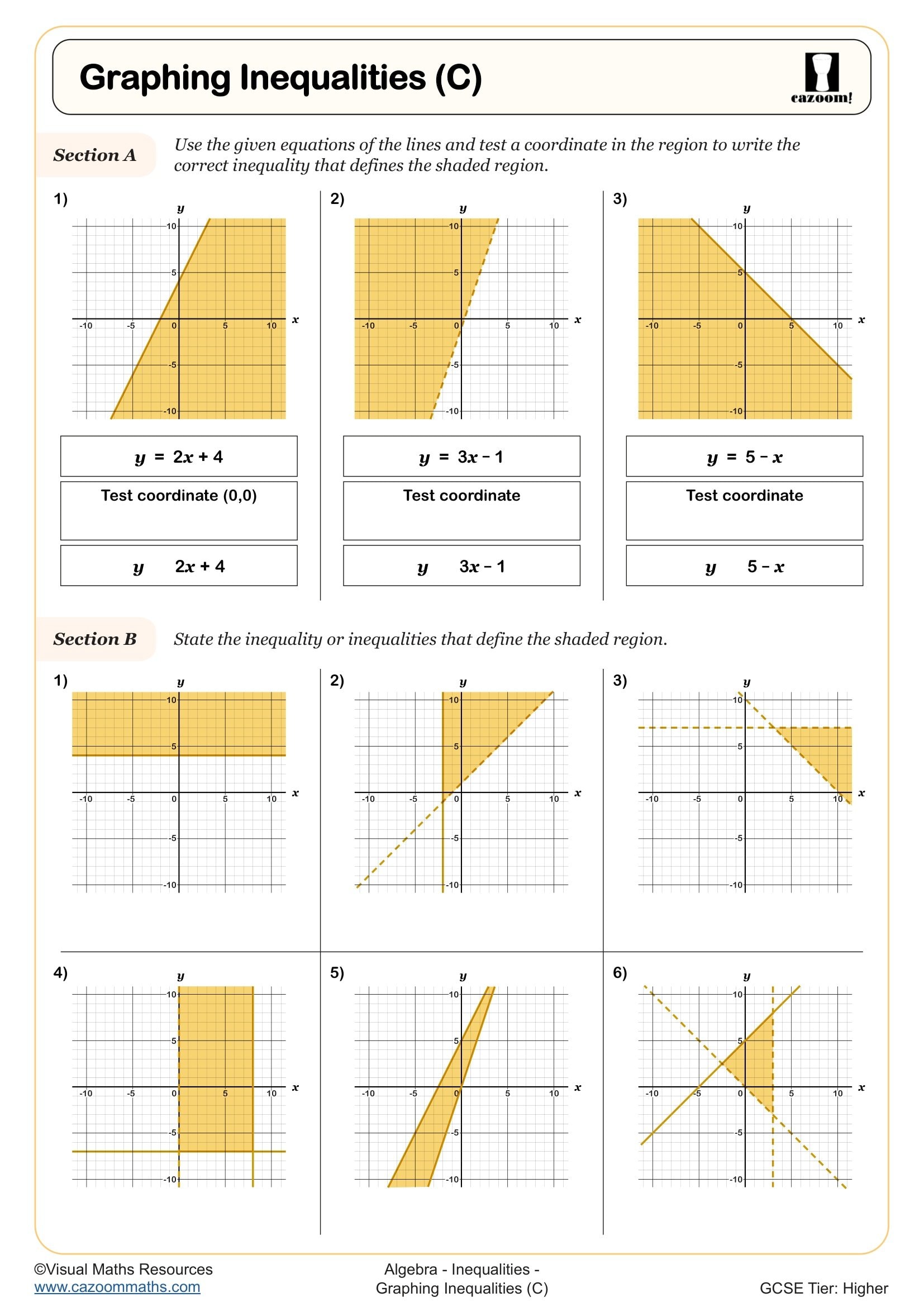
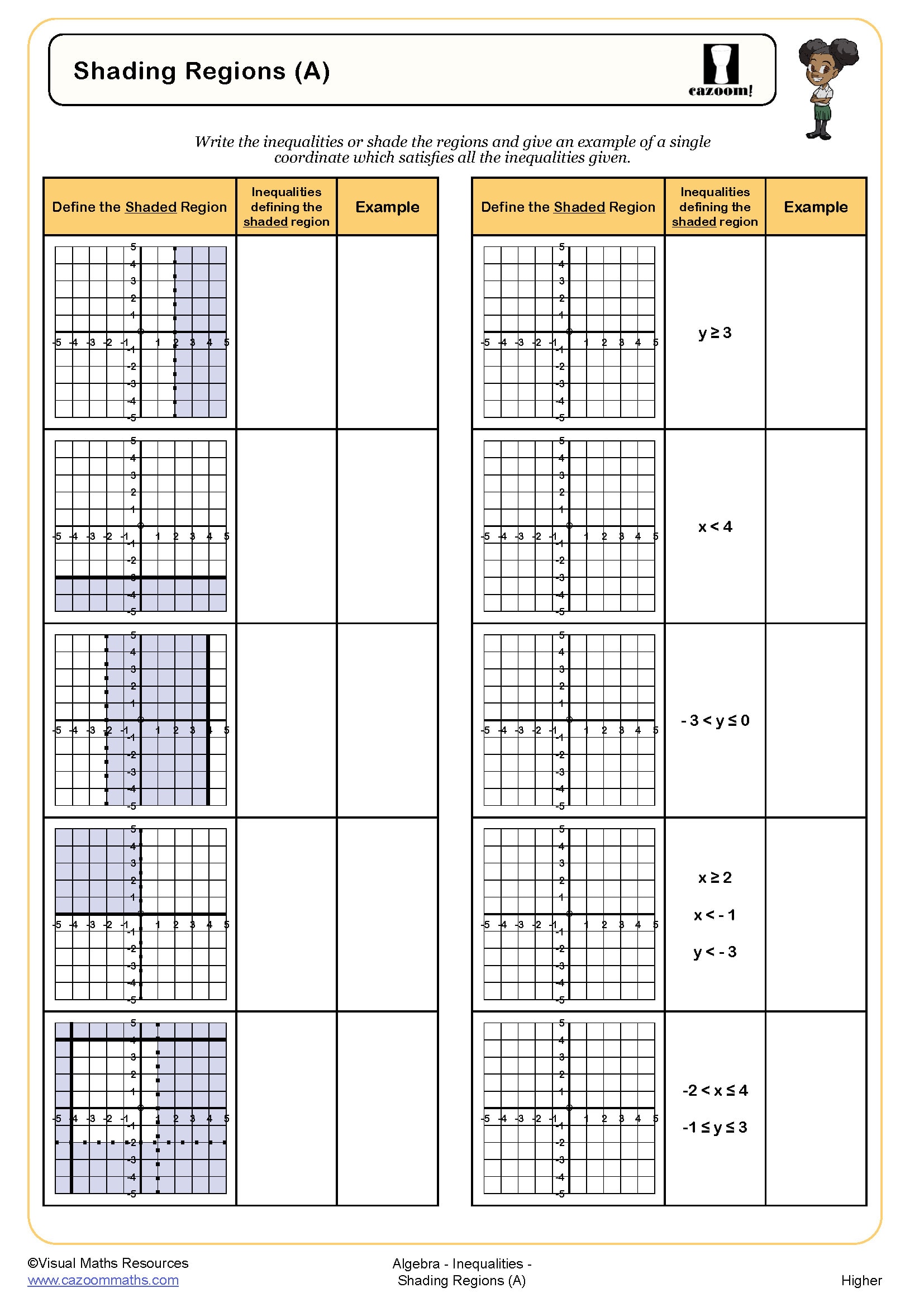
The progression in Year 11 focuses on increased complexity and exam technique. Students move from straightforward one-step inequalities to multi-step problems requiring careful manipulation, including those with negative coefficients and fractional solutions. The collection includes practice with problems where students must satisfy two inequalities simultaneously without sketching graphs, a skill that connects to later work on linear programming and appears regularly in GCSE questions worth multiple marks.
How do you solve problems involving two inequality conditions?
When satisfying two inequalities, students must find the range of values that makes both statements true simultaneously. For example, if x > 2 and x ≤ 7, the solution is the overlap: 2 < x ≤ 7. Students need to solve each inequality separately first, then identify where the solution sets intersect. Teachers observe that sketching both solutions on parallel number lines helps students visualise the overlap, though exam questions sometimes specifically ask students to solve without sketching, testing pure algebraic reasoning.
This skill has direct applications in manufacturing and quality control, where products must meet multiple specification limits simultaneously. A component might need to be between 4.8mm and 5.2mm in diameter (4.8 ≤ d ≤ 5.2) whilst also being within temperature tolerances. Engineers use compound inequalities to define acceptable ranges, and any measurement falling outside these parameters triggers rejection. Understanding how to work with two inequality conditions prepares students for real-world contexts where multiple constraints operate at once.
How can teachers use these worksheets effectively in lessons?
The worksheets provide structured practice that builds from solving linear inequalities through to more complex problems involving two conditions. Each sheet follows a logical progression, allowing students to consolidate foundational manipulation skills before tackling compound inequalities. The included answer sheets enable students to work independently, checking their solutions step-by-step and identifying exactly where errors occur, which develops self-correction habits that prove valuable during exam preparation.
Many teachers use these resources for differentiated revision sessions, assigning specific sheets based on diagnostic assessment results. The collection works well for intervention groups targeting students on Foundation tier grade boundaries who need focused practice on inequality sign manipulation. The worksheets also suit homework assignments where students can attempt problems independently with answer sheets available for self-marking, freeing up lesson time for addressing misconceptions. Paired work sessions where students compare solutions and justify their sign reversals help surface common errors before they become embedded.