Year 11 Non-linear Graphs Worksheets
What are non-linear graphs in Year 11 maths?
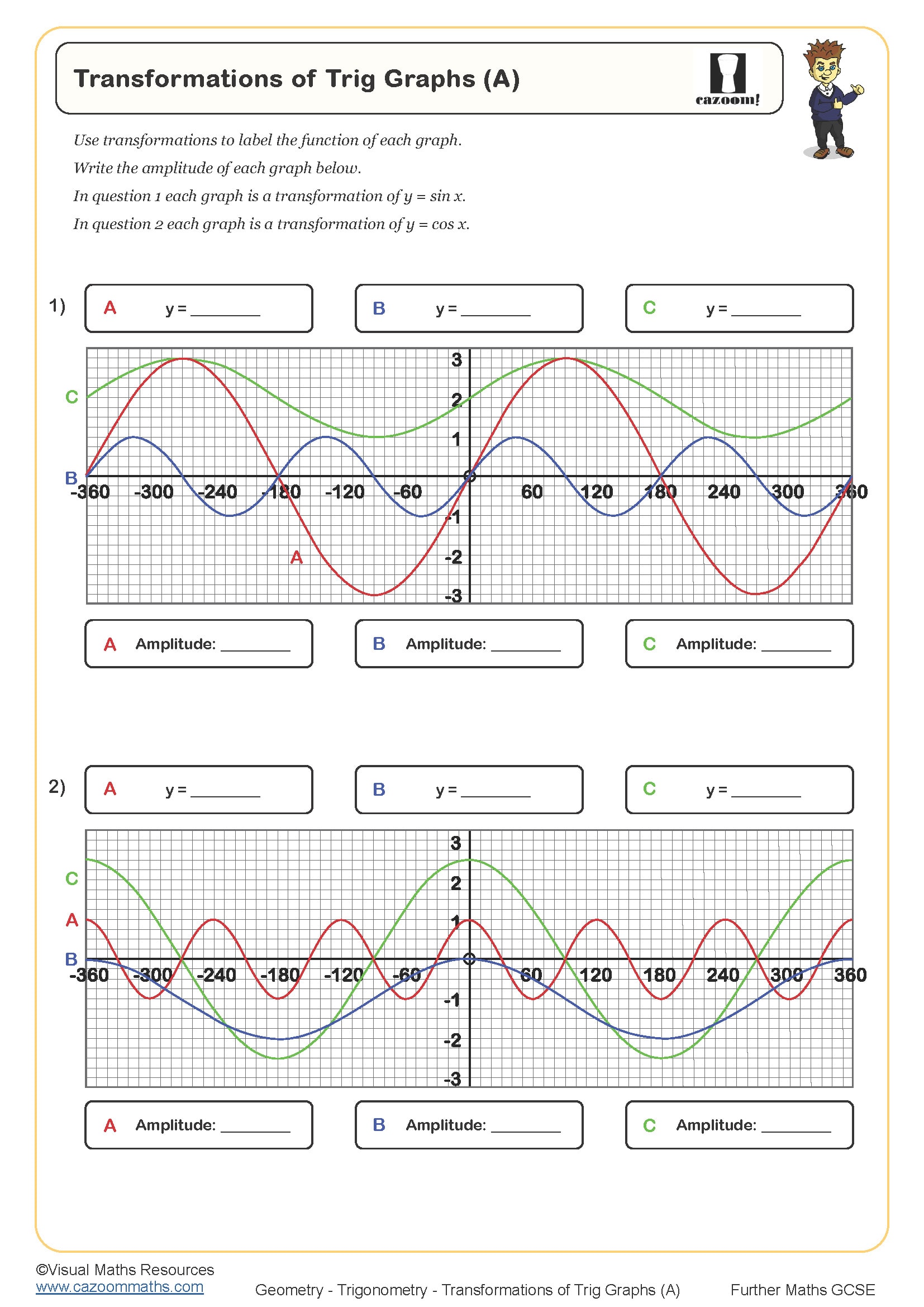
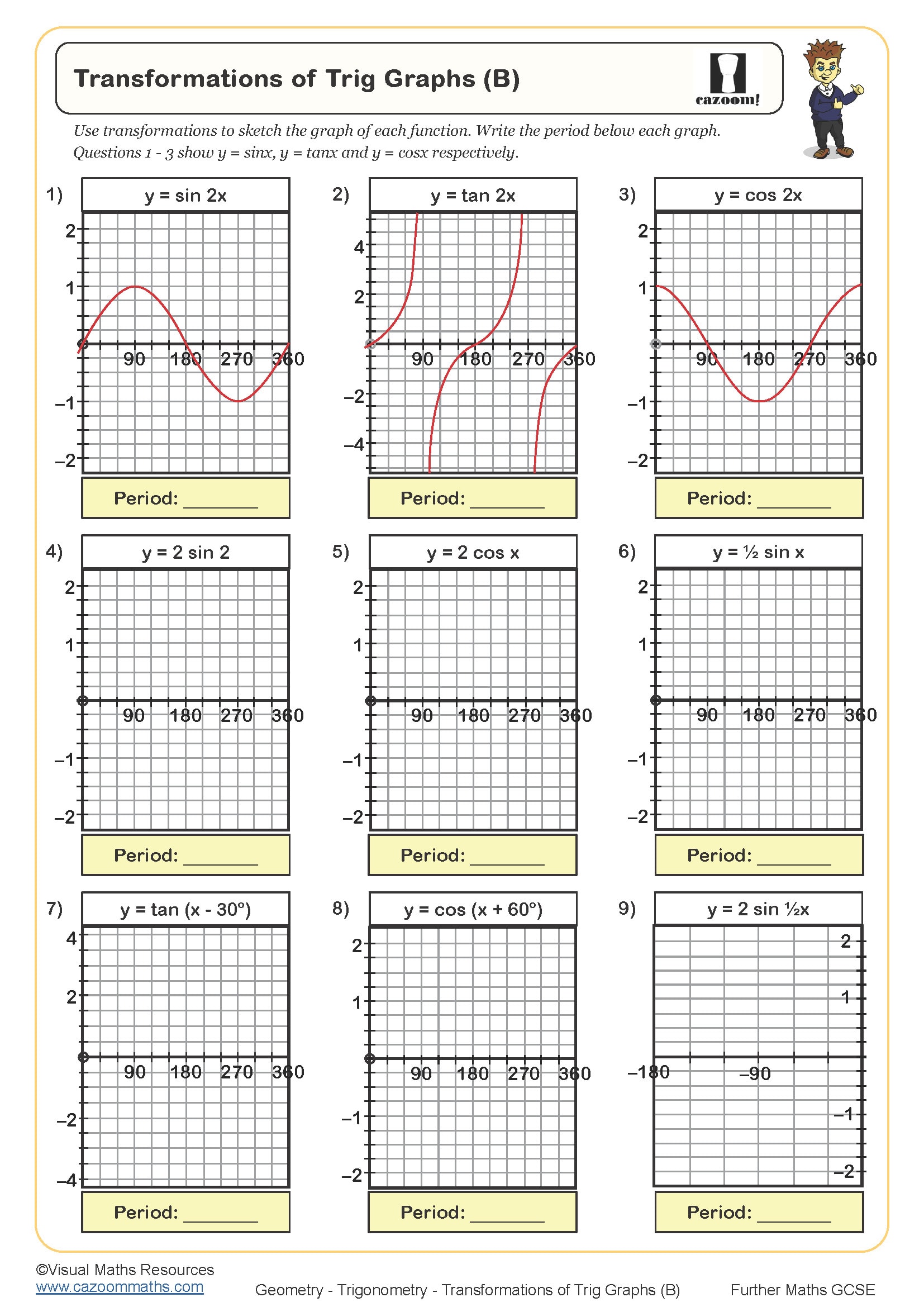
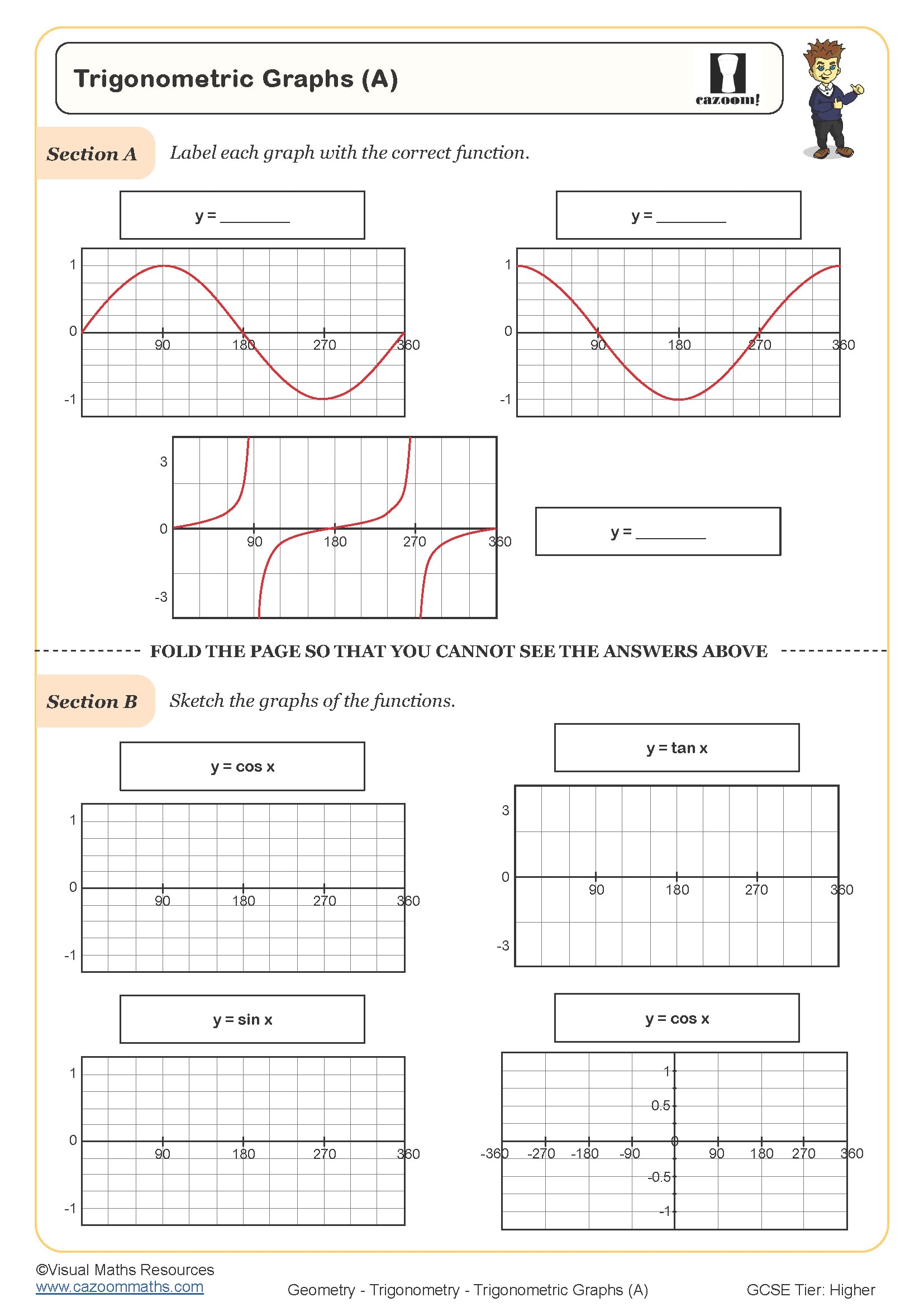
Non-linear graphs are curves rather than straight lines, representing relationships where the rate of change isn't constant. At Year 11, students work with quadratic graphs (parabolas), cubic graphs, reciprocal graphs (hyperbolas) and exponential graphs, learning to sketch each family from equations and identify their characteristic shapes. The National Curriculum for KS4 expects students to recognise these functions algebraically and graphically, finding key features like intercepts, turning points and asymptotes.
A common misconception is that all U-shaped curves are quadratics. Students often misidentify y = 1/x² as quadratic because it creates a symmetrical curve, when it's actually a reciprocal function with asymptotes at both axes. Exam mark schemes expect clear distinction between graph families, and students lose marks when they sketch curves without showing asymptotic behaviour or fail to mark the position of turning points accurately on the coordinate grid.
Which year groups study non-linear graphs?
This collection targets Year 11 students at KS4, typically those working towards GCSE Higher tier where non-linear graphs form a substantial component of the algebra and functions content. Students encounter quadratics in Year 9 and Year 10, but Year 11 work extends to comparing multiple graph families, transformations of curves, and using graphs to solve equations graphically. The topic appears in Paper 1 (non-calculator) and Paper 2 (calculator), requiring both sketching skills and interpretation.
The difficulty progression focuses on moving from plotting individual graphs to comparing families, applying transformations, and solving simultaneous equations where one is linear and one is quadratic. Year 11 students must also interpret gradients of curves at specific points, linking graphical work to rates of change in real contexts. Teachers often find that revisiting simpler quadratics before introducing reciprocal and exponential functions helps students build confidence with the underlying coordinate geometry skills needed for accurate curve sketching.
How do you sketch a reciprocal graph accurately?
Sketching reciprocal graphs like y = 1/x or y = k/x requires understanding asymptotic behaviour. Students should recognise that as x approaches zero, y tends towards infinity (or negative infinity), and as x gets very large, y approaches zero. The graph never touches the axes, creating two separate branches in opposite quadrants. Marking asymptotes as dotted lines along the x and y axes helps students visualise the boundaries, then plotting a few key points in each quadrant (such as x = 1, 2, -1, -2) allows accurate curve sketching through those coordinates.
Reciprocal relationships appear throughout science and engineering contexts. In physics, the relationship between pressure and volume in Boyle's Law follows a reciprocal pattern, where doubling the volume halves the pressure. In electronics, resistance and conductance show reciprocal behaviour. Understanding that reciprocal graphs never reach zero helps students interpret real situations where quantities decrease towards a limit but never disappear entirely, such as medication concentration in the bloodstream over time.
How do these worksheets support GCSE preparation?
The worksheets build skills systematically, starting with recognising graph shapes from equations before progressing to sketching curves with marked key features and interpreting graphs to solve problems. This scaffolding mirrors the approach GCSE questions take, where early marks come from basic identification while higher marks require accurate sketching and problem-solving. Having complete answer sheets allows students to self-assess their curve sketching, checking whether they've correctly identified asymptotes, turning points and intercepts that examiners specifically look for.
Many teachers use these resources during targeted intervention sessions with students who confuse different curve families, as the visual comparison across worksheets helps consolidate recognition. The worksheets work effectively as homework following taught lessons, giving students independent practice before attempting past paper questions. In revision sessions, paired work where one student sketches while the other checks against answers encourages discussion about why certain features appear, strengthening conceptual understanding alongside procedural fluency needed for exam success.