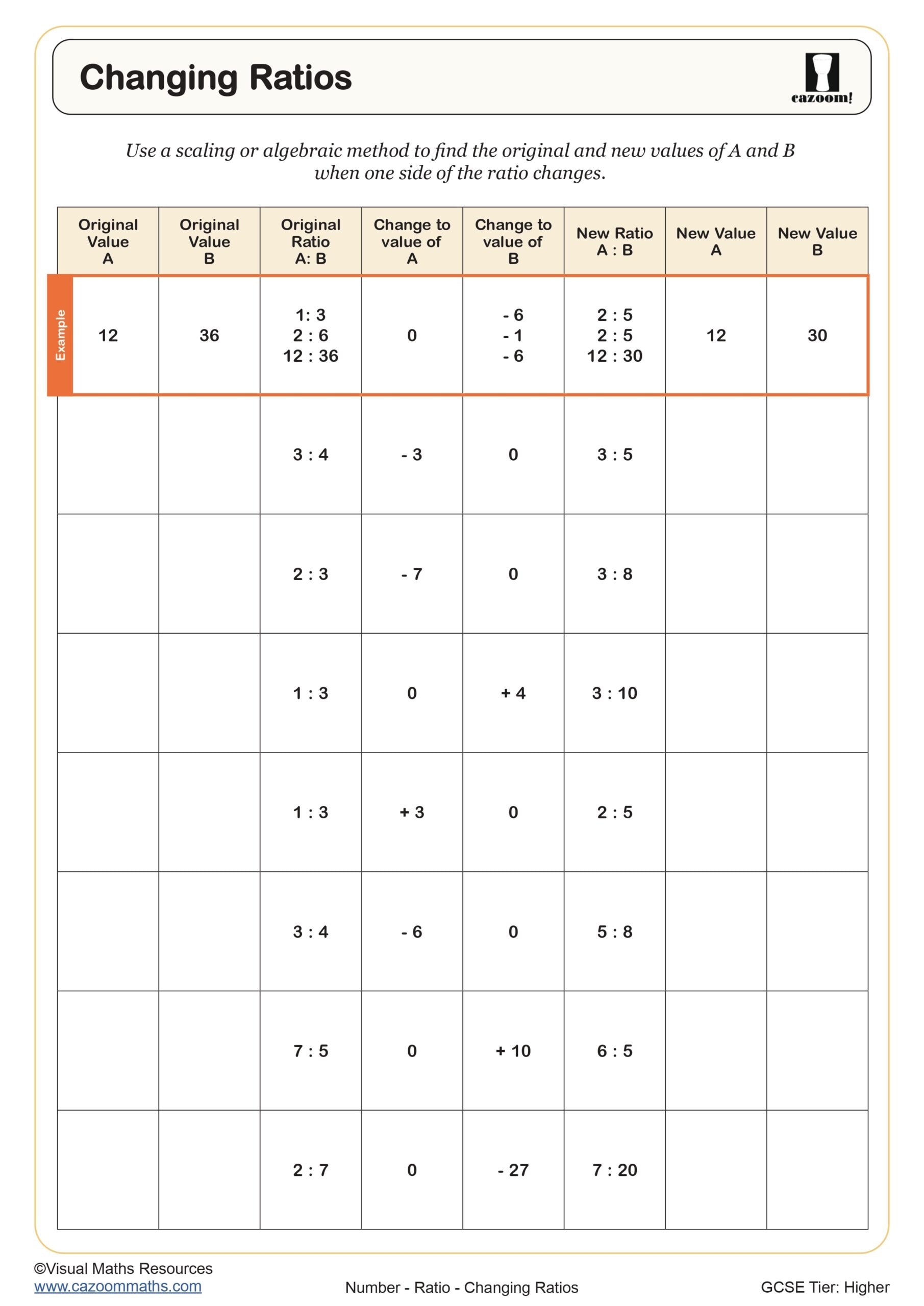
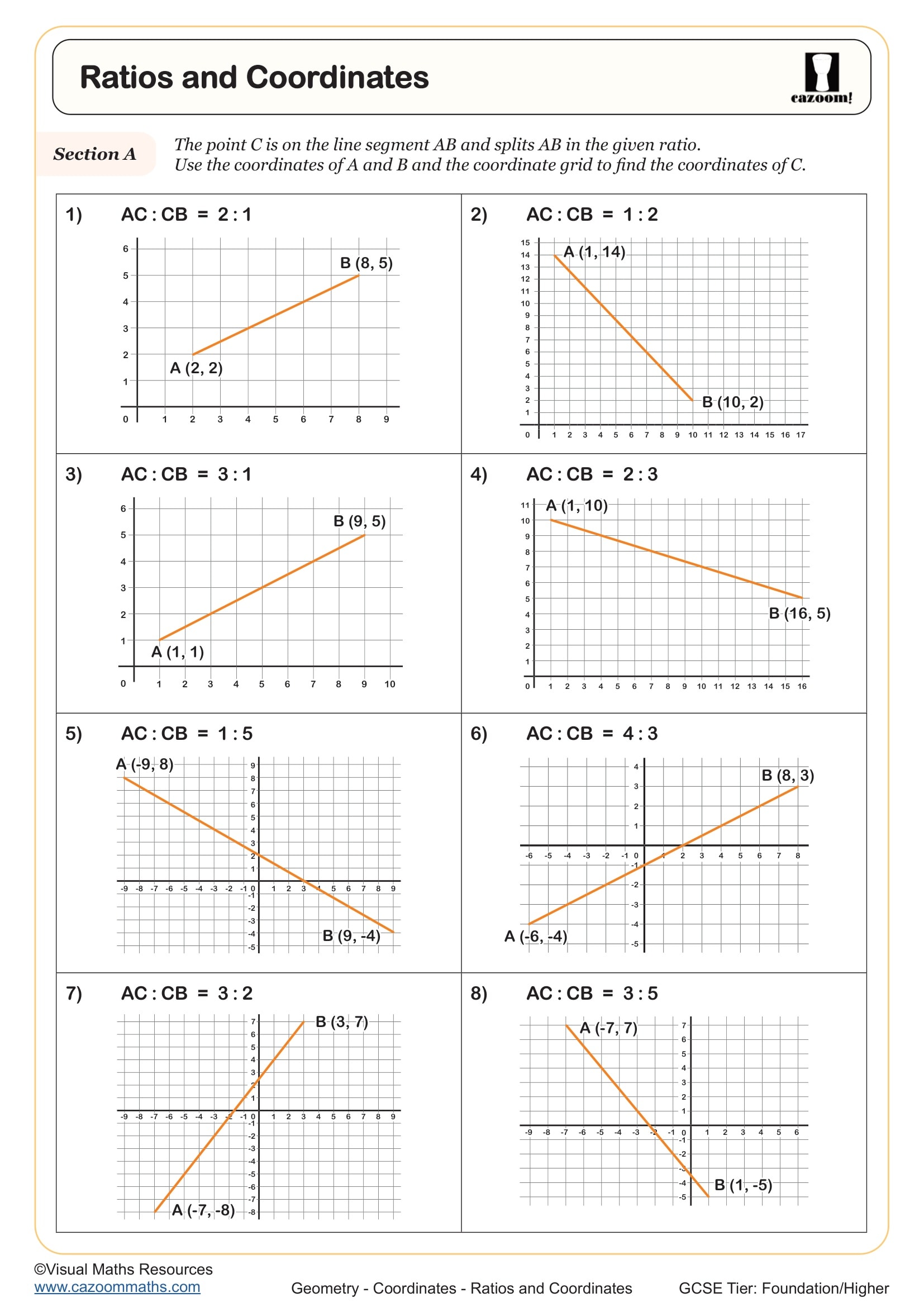
Year 11 Ratio Worksheets
What is rationalising the denominator in ratio problems?
Rationalising the denominator involves rewriting a fraction so the denominator contains no surds or irrational numbers. In ratio contexts, this technique appears when students simplify expressions or compare quantities involving square roots. At GCSE higher tier, exam questions often present ratios in surd form and expect students to rationalise as part of simplification or to facilitate comparison between values.
A common error occurs when students attempt to rationalise binomial denominators like (3 + √2) by only multiplying by √2 rather than using the conjugate (3 - √2). Exam mark schemes specifically award method marks for correctly identifying and applying the conjugate, so students who miss this step lose marks even if subsequent working is accurate. Teachers report that explicitly teaching the difference-of-two-squares pattern helps students recognise why the conjugate eliminates the surd term.
Which year groups study advanced ratio with algebraic expressions?
These ratio worksheets are designed for Year 11 students working at KS4 higher tier level. At this stage, the National Curriculum expects students to manipulate algebraic ratios and apply surds confidently within ratio contexts. This work extends simpler ratio skills from earlier key stages, now requiring students to combine multiple techniques within single problems.
The progression from KS3 into Year 11 involves moving from numerical ratios to algebraic expressions, then incorporating surds and binomial forms. Students who mastered basic ratio sharing and scaling in Years 7-9 now encounter problems where they must algebraically manipulate before applying ratio techniques. The worksheets reflect this increased complexity, with later questions combining rationalisation with fraction operations and requiring multiple steps to reach simplified form.
How does ratio connect to real-world STEM applications?
Ratio provides the mathematical foundation for countless scientific calculations, from chemical concentration to engineering scale factors. In chemistry, students use ratio to determine reactant quantities in stoichiometry, whilst physics applications include gear ratios, velocity ratios in pulley systems, and aspect ratios in optics. Understanding algebraic ratio manipulation prepares students for A-level sciences where they'll encounter proportional relationships expressed through formulae rather than simple numbers.
The rationalising techniques practised in these worksheets directly support scientific notation and standard form work. Engineers frequently rationalise denominators when simplifying impedance calculations in electrical circuits or when working with wave mechanics in physics. Students who can confidently manipulate surds within ratios find transition to further maths and physics courses considerably smoother, as these subjects assume fluency with algebraic fraction manipulation and exact form answers rather than decimal approximations.
How can teachers use these ratio worksheets in lessons?
The worksheets scaffold progression from understanding fraction operations within ratio contexts through to complex binomial rationalisation. Teachers can use the initial worksheets to diagnose whether students have secure foundational skills before introducing surds, whilst later sheets provide targeted practice on exam-style questions involving multiple steps. The included answer sheets allow students to self-check working and identify exactly where errors occur in multi-step problems.
Many teachers deploy these resources during GCSE intervention sessions, particularly for students whose algebra or fraction skills need strengthening before tackling rationalising. The worksheets work well for paired problem-solving, where one student attempts a question whilst their partner checks against the answer sheet and explains any errors. For revision, teachers often assign specific subtopic sheets based on mock exam analysis, targeting the precise skills where individual students lost marks rather than generic ratio practice.