Year 11 Sequences Worksheets
What should students know about quadratic sequences for GCSE?
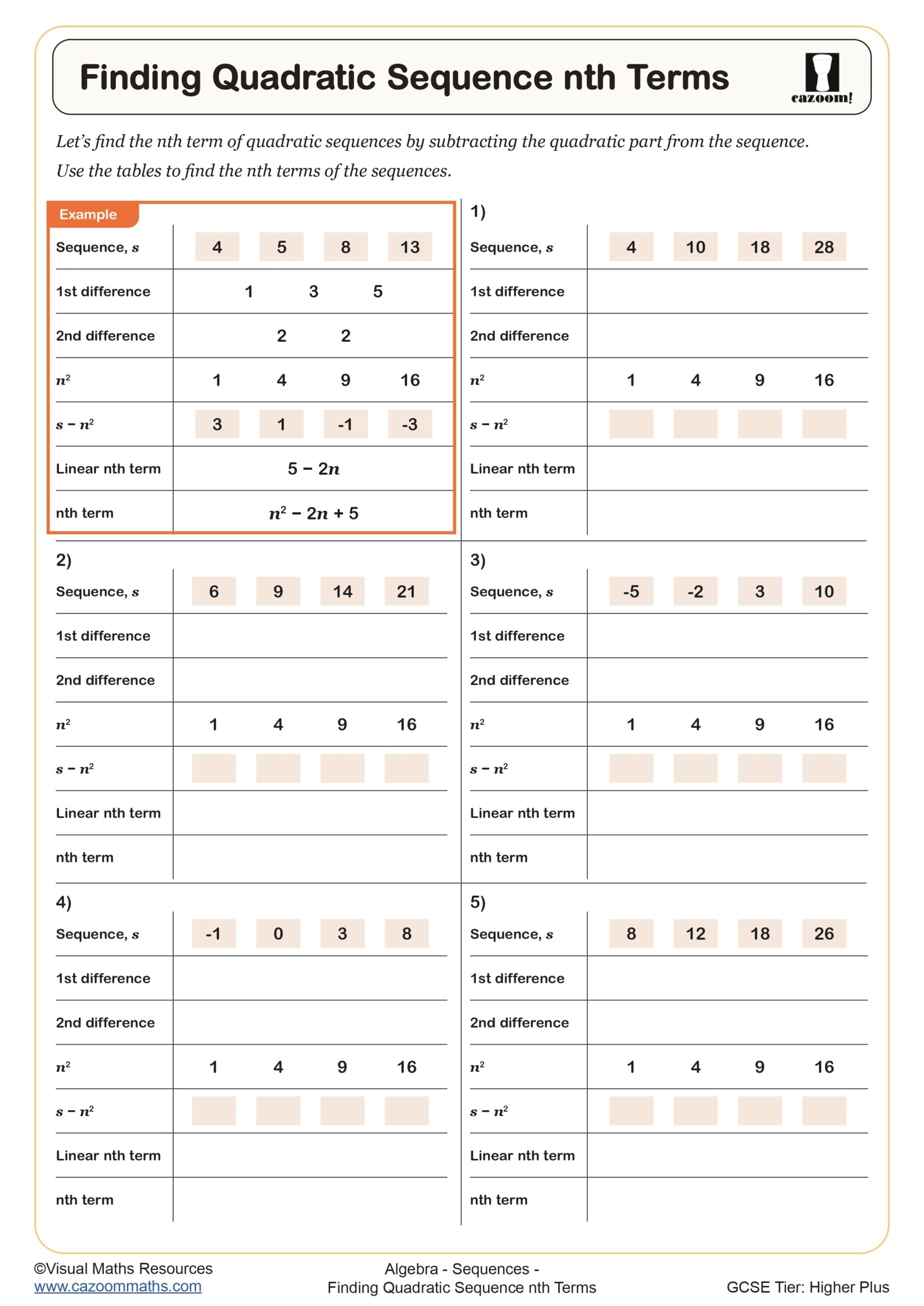
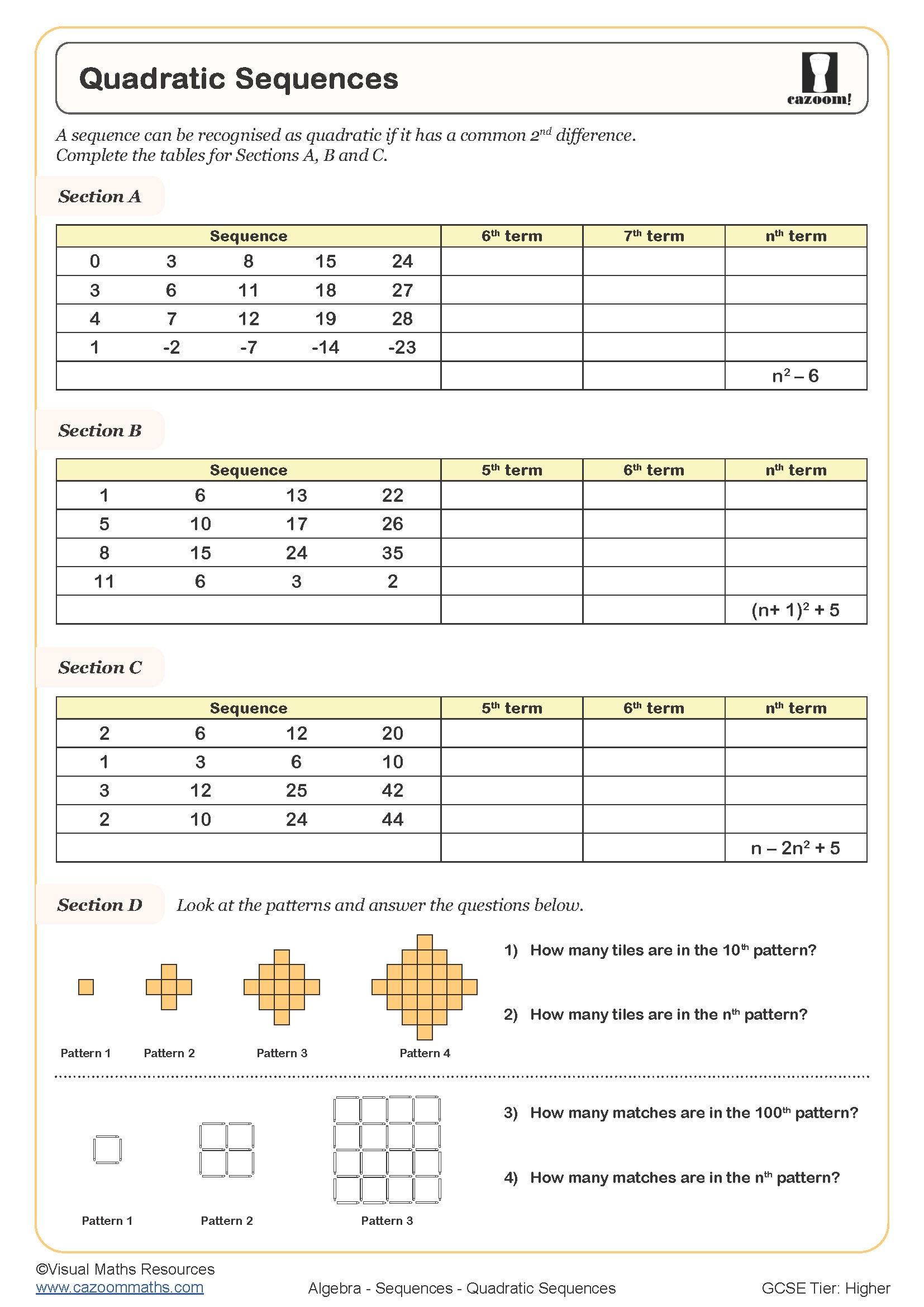
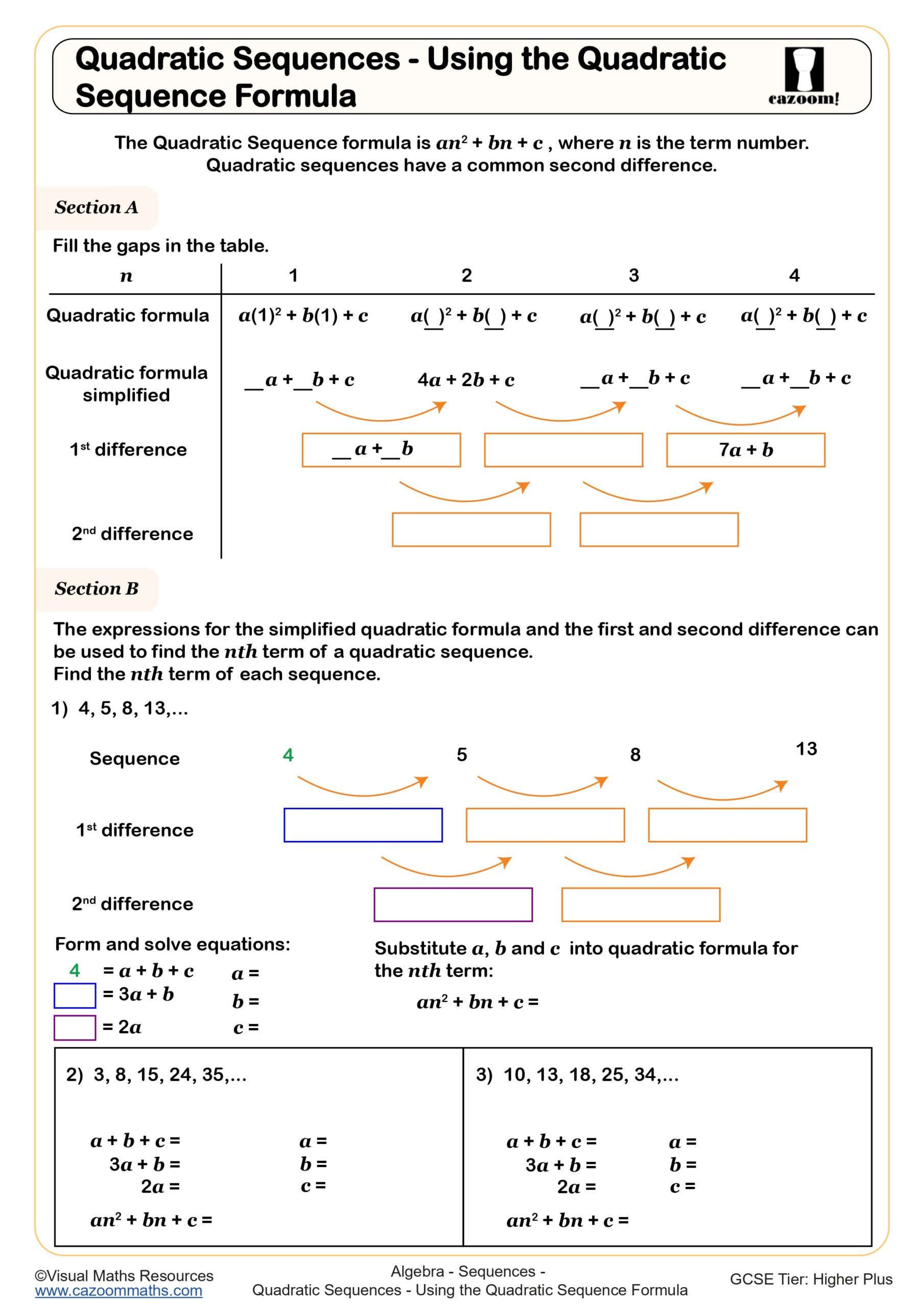
Quadratic sequences appear on Higher tier GCSE papers and require students to recognise patterns where the second difference is constant. A quadratic sequence worksheet PDF typically includes finding the nth term formula (which takes the form an² + bn + c), identifying whether sequences are quadratic by checking differences, and generating terms from given formulas. Students need to distinguish these from linear sequences where only the first difference matters.
The most common error occurs when students try to use linear methods on quadratic sequences, finding the first difference and assuming that's sufficient. Exam mark schemes expect students to show the second difference explicitly and work systematically through the coefficient of n², then adjust for the linear and constant terms. Many students lose marks by rushing this process or not showing the difference row clearly in their working.
Which year groups study sequences at KS4?
Sequences form part of the KS4 algebra curriculum, with Year 11 students consolidating and extending the sequence work begun in previous years. By this stage, students tackle arithmetic sequences with negative or fractional common differences, geometric sequences with multipliers less than one, and quadratic sequences on the Higher tier. The focus shifts from simple pattern-spotting to algebraic manipulation and proof.
The progression intensifies significantly in Year 11 as exam preparation demands fluency across all sequence types simultaneously. Students move from routine nth term questions to problems that combine sequences with other algebraic skills, such as solving equations involving sequence terms or proving properties of sequences. Higher tier students also encounter Fibonacci-type sequences and recurrence relations that require different reasoning approaches.
How do geometric sequences connect to real-world contexts?
Geometric sequences model situations involving repeated multiplication, where each term is found by multiplying the previous term by a constant ratio. Students work with formulas like un = ar^(n-1) to find specific terms and calculate values in practical contexts. Understanding the common ratio and how it affects growth or decay patterns underpins work with exponential functions encountered later in A-level mathematics.
These sequences appear throughout science and finance in ways that make the mathematics tangible for students. Population growth models, compound interest calculations, radioactive decay, and drug concentration in the bloodstream all follow geometric patterns. In computing, geometric sequences describe data storage doubling and algorithm efficiency. When students recognise that halving medication concentration each day follows a geometric sequence with ratio 0.5, the abstract notation gains meaning and relevance to careers in healthcare and pharmaceutical sciences.
How do these worksheets support exam preparation?
The worksheets build fluency through structured question sets that mirror GCSE exam style and demand. Students encounter the full range of sequence types they'll meet in papers, with questions progressing from straightforward term generation to more complex nth term problems and reasoning tasks. Having answer sheets for every question allows students to identify misconceptions immediately and understand where their method breaks down, rather than simply marking answers right or wrong.
Many teachers use these resources strategically during Year 11 intervention sessions, assigning specific sequence types based on mock exam analysis. The worksheets work well for homework when students need focused practise on a particular weakness, or as starter activities to maintain fluency throughout the revision period. Paired work proves effective when one student works through a problem whilst explaining their reasoning, then partners check against the answer sheet together - this verbalisation often reveals gaps in understanding that silent practise misses.