Menu

PRIMARYSECONDARYGCSE REVISIONPRICINGSEARCHHELP
LOGINSIGN UP

Year 11 Surds Worksheets

Add and Subtract Surds

Preview of Add and Subtract Surds

Rationalising Surds (D)

Preview of Rationalising Surds (D)

Rationalising the Denominator - First Steps

Preview of Rationalising the Denominator - First Steps

Rationalising the Denominator - with Binomial Denominators

Preview of Rationalising the Denominator - with Binomial Denominators

Rationalising the Denominator - with Binomial Numerators

Preview of Rationalising the Denominator - with Binomial Numerators

Simplifying Surds (A)

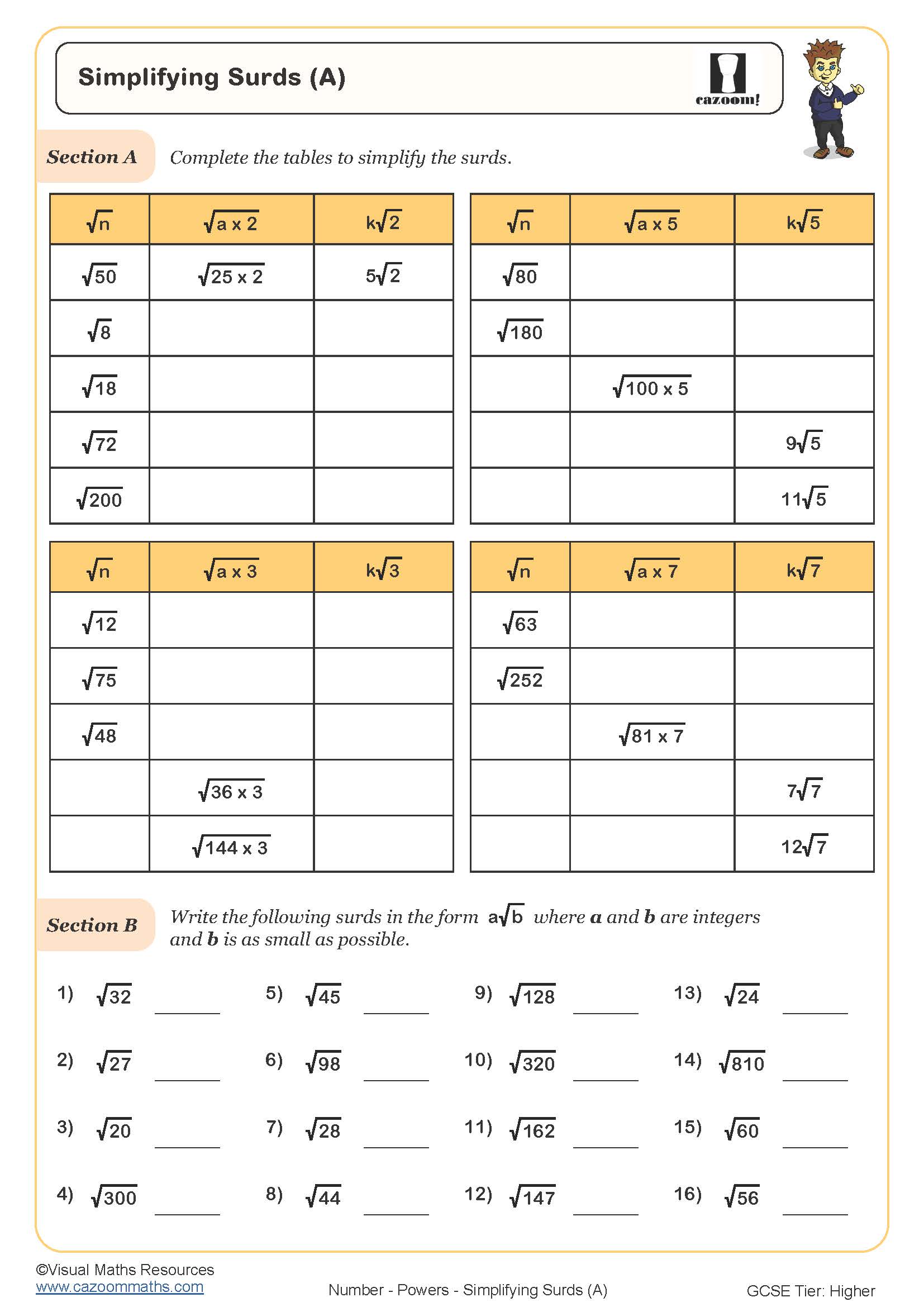
Preview of Simplifying Surds (A)

Simplifying Surds (B)

Preview of Simplifying Surds (B)

Simplifying Surds with Brackets (C)

Preview of Simplifying Surds with Brackets (C)

Writing Exact Answers Using Surds

Preview of Writing Exact Answers Using Surds