Year 7 Directed Number Counters Worksheets
All worksheets are created by the team of experienced teachers at Cazoom Maths.
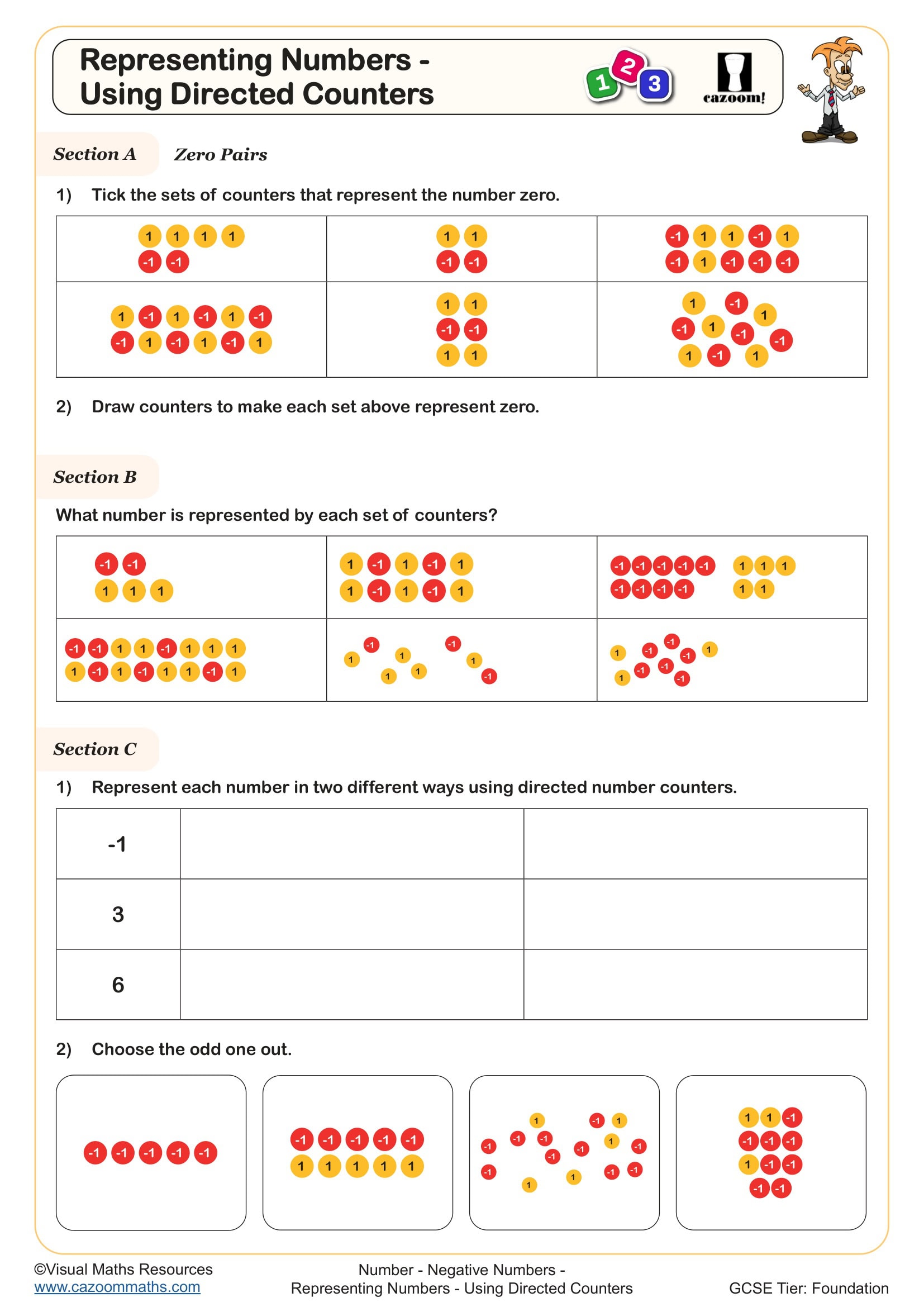
What are directed number counters in maths?
Directed number counters use coloured counters to represent positive and negative values, providing a visual model for operations with integers. Typically, one colour represents positive numbers whilst another represents negative numbers, with the understanding that a positive and negative counter together form a 'zero pair' that cancels out. This concrete approach aligns with Key Stage 3 expectations for developing fluency with negative numbers before progressing to algebraic manipulation.
The counter model proves particularly valuable when students tackle multiplication involving negative numbers. Teachers often observe that students can follow the rule 'negative times negative equals positive' without understanding why, leading to errors when sign patterns become more complex. The counter method shows, for example, that multiplying -3 by -2 means removing three groups of two negative counters, leaving six positive counters behind after zero pairs are eliminated.
Which year groups use directed number counters?
Directed number counters appear primarily in Year 7 as students transition from primary mathematics into the Key Stage 3 curriculum. At this stage, the National Curriculum requires students to use and apply the four operations with both positive and negative integers, and counter models provide the conceptual foundation before moving to purely symbolic methods. This visual approach supports students who need concrete representations alongside abstract mathematical rules.
Whilst Year 7 introduces the counter method, the understanding developed here supports progression through later years. Students move from manipulating physical or drawn counters to visualising the process mentally, then eventually internalising the sign rules without needing the model. This progression mirrors the concrete-pictorial-abstract approach, ensuring students develop robust understanding rather than fragile procedural knowledge that breaks down under exam pressure.
How do counters help with multiplication of directed numbers?
Counter models make multiplication of directed numbers meaningful by representing the operation as repeated addition or removal of groups. For positive multiplications like 3 × -2, students add three groups of two negative counters, giving -6. For negative multiplications like -3 × -2, students remove three groups of two negative counters from a collection, which requires first creating zero pairs, then taking away the negative counters to leave six positive counters remaining.
This understanding connects directly to applications in science and finance where direction matters. Temperature changes provide a clear context: if temperature decreases by 2°C each hour (a rate of -2°C per hour), then three hours ago (going back in time, represented by -3), the operation -3 × -2 shows the temperature was 6°C higher than now. The counter model reveals why reversing a negative process produces a positive outcome, giving students conceptual grounding that supports problem-solving across STEM subjects.
How should teachers use these directed number worksheets?
The worksheets build understanding systematically, starting with straightforward multiplication patterns using counters before progressing to questions requiring students to explain their reasoning. This structure supports teachers in identifying where conceptual understanding breaks down, as students who can calculate answers but cannot explain the counter model often revert to memorised rules that fail in unfamiliar contexts. The visual nature of counter work makes these worksheets particularly valuable for differentiation and intervention.
Many teachers use these resources during initial teaching with paired work, where one student demonstrates the counter model whilst the partner records the calculation symbolically, then they swap roles. The complete answer sheets enable students to self-check during independent practise or homework, whilst also providing worked examples for students who need additional support. Teachers often set selected questions as low-stakes assessments to gauge whether students can transfer counter understanding to purely numerical problems before moving on to more abstract directed number work.