Year 7 Volume and Surface Area Worksheets
What do Year 7 students learn about volume and surface area?
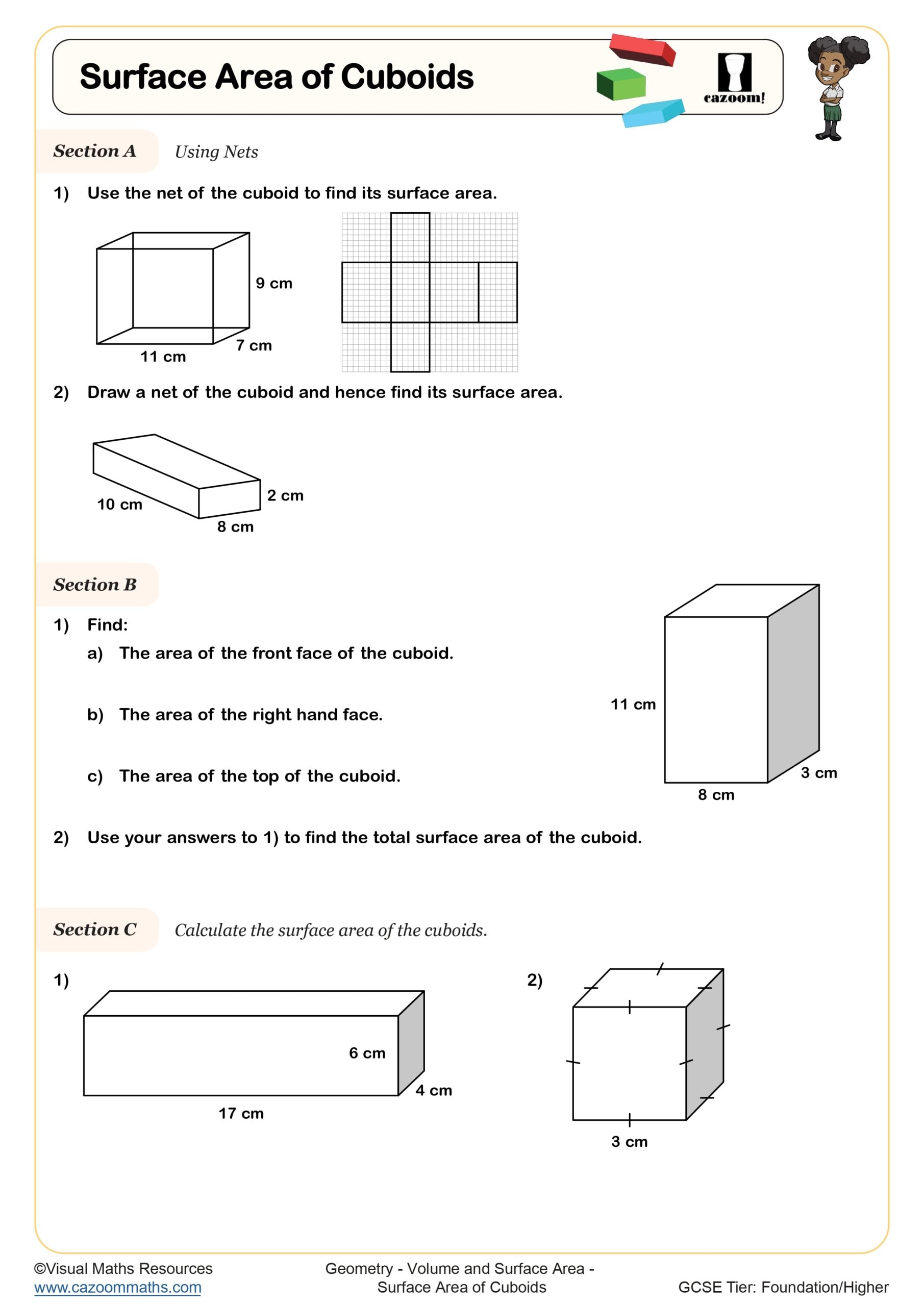
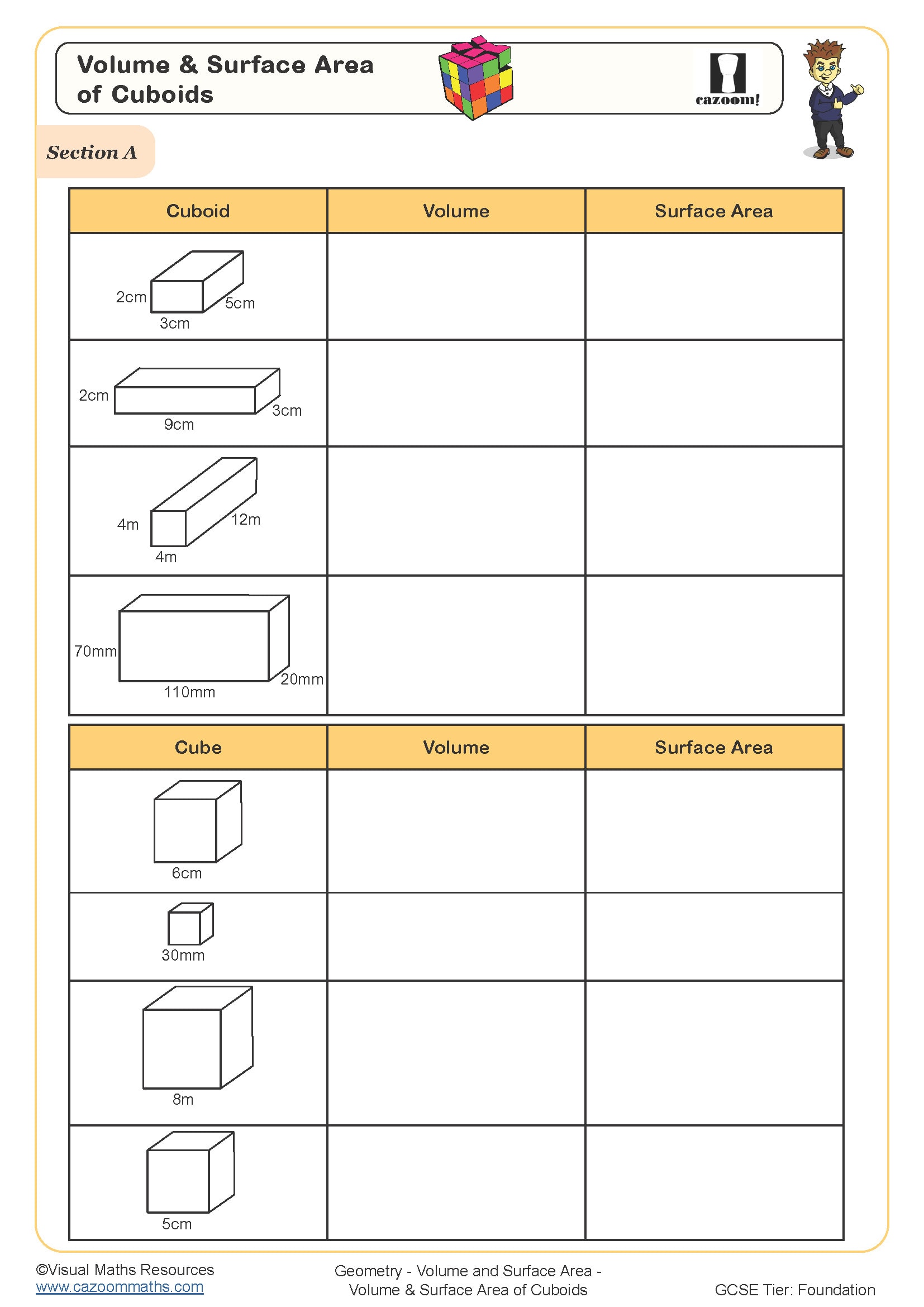
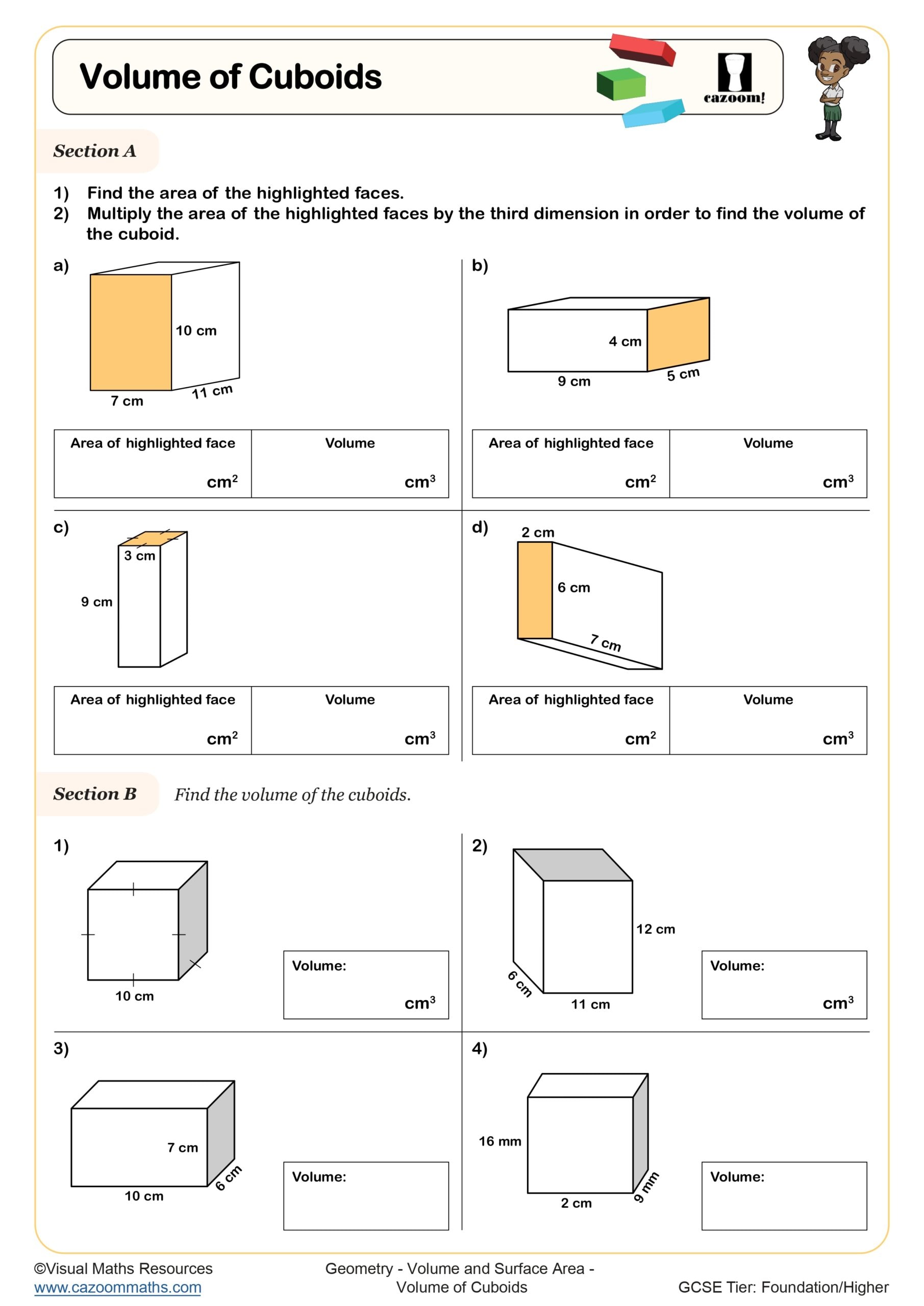
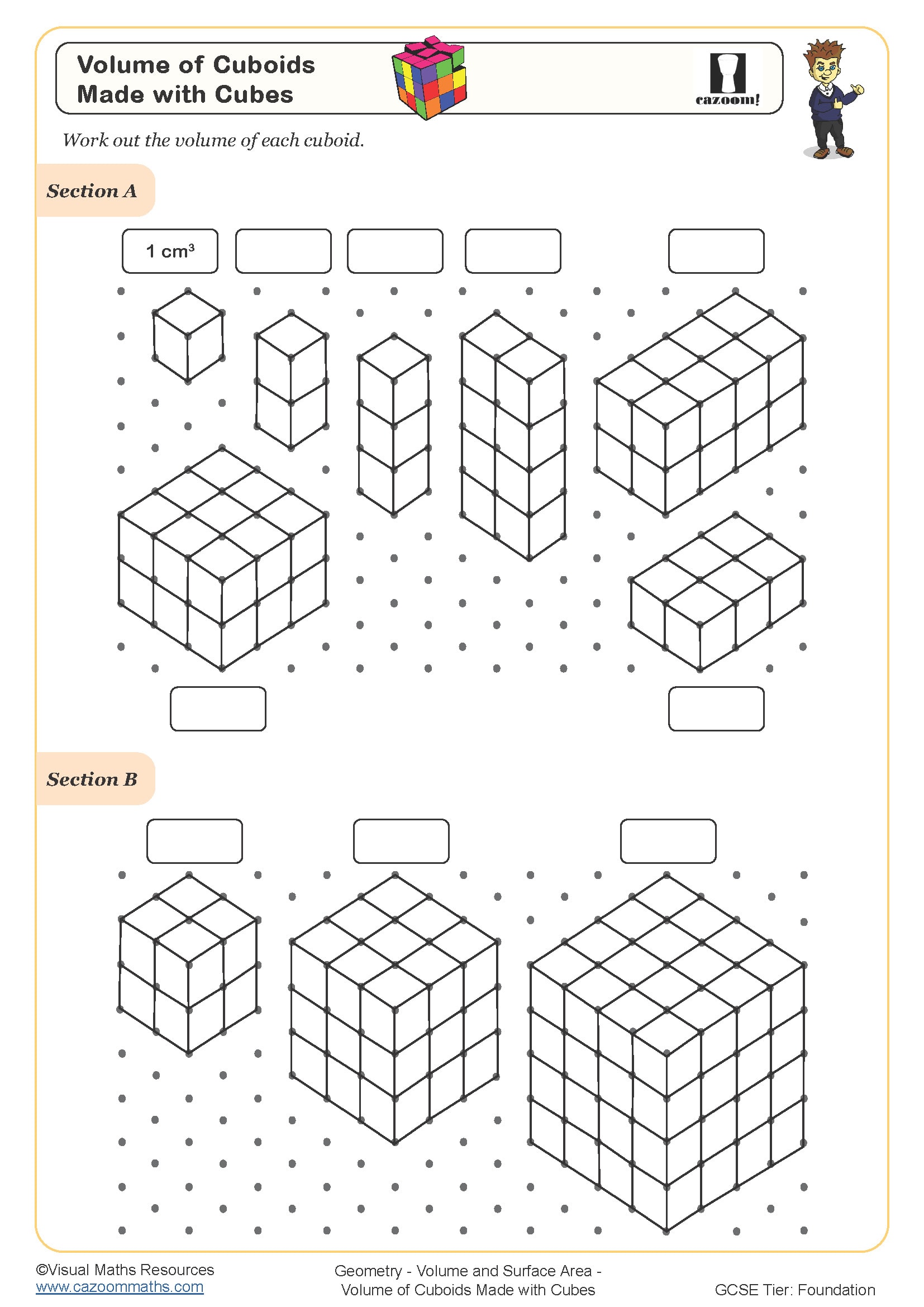
At Year 7 within KS3, students extend their primary knowledge of volume to include surface area calculations for cuboids, then progress to more complex solids including pyramids and spheres. The National Curriculum expects students to recall and apply formulae for volume and surface area, understanding that volume measures space inside a shape whilst surface area measures the total external coverage.
Students typically lose marks on exam questions when they substitute values incorrectly into formulae or forget to square radius values when calculating sphere surface area (4πr²). Teachers often observe that students struggle most with pyramids, where they must identify which measurements represent base dimensions versus slant height, particularly when diagrams show shapes from different orientations.
Which year groups study volume and surface area?
These worksheets are designed specifically for Year 7 students within Key Stage 3, where volume and surface area form part of the geometry and measures strand. This topic typically appears in the second half of Year 7 after students have consolidated their understanding of area and perimeter of two-dimensional shapes.
The progression across KS3 sees Year 7 students working with standard formulae for common solids, Year 8 students tackling composite shapes and frustums, and Year 9 students applying these skills to problem-solving contexts including real-world applications. By introducing pyramids and spheres at Year 7, students build the foundation needed for more complex three-dimensional work required at GCSE, where volume and surface area questions regularly appear on both Foundation and Higher papers.
How do you calculate the surface area of a pyramid?
Surface area of a pyramid requires students to calculate the area of the base plus the areas of all triangular faces. For a square-based pyramid, this means finding the area of the square base (side²) and adding four identical triangular faces (each with area ½ × base × slant height). Students must distinguish between the perpendicular height (used for volume) and slant height (used for surface area calculations).
Architects and structural engineers regularly calculate pyramid surface areas when designing roofs, church spires, or modern buildings with pyramidal features. Understanding these calculations connects directly to materials estimation: knowing the surface area determines how much roofing material, cladding, or reflective coating is required. The Louvre Pyramid in Paris, for instance, required precise surface area calculations to determine the quantity of glass panels needed during construction.
How do these worksheets help students practise volume and surface area?
The worksheets provide structured practice moving from straightforward calculations with given formulae to more challenging problems where students must identify which formula applies to each solid. Questions progress from cuboids with integer dimensions through to spheres requiring decimal approximations, allowing students to build confidence systematically. The included answer sheets show not just final answers but intermediate steps, helping students identify where errors occur in multi-step calculations.
Teachers use these worksheets effectively for differentiated homework, setting different sections to students based on their confidence levels, or for targeted intervention with small groups who need additional practice before assessments. The clear progression makes them valuable for revision lessons, where students can work through problems independently whilst teachers circulate to address individual misconceptions, or for paired work where students can discuss which formula applies before calculating.