Year 8 Directed Number Counters Worksheets
All worksheets are created by the team of experienced teachers at Cazoom Maths.
What Are Directed Number Counters and How Do They Work?
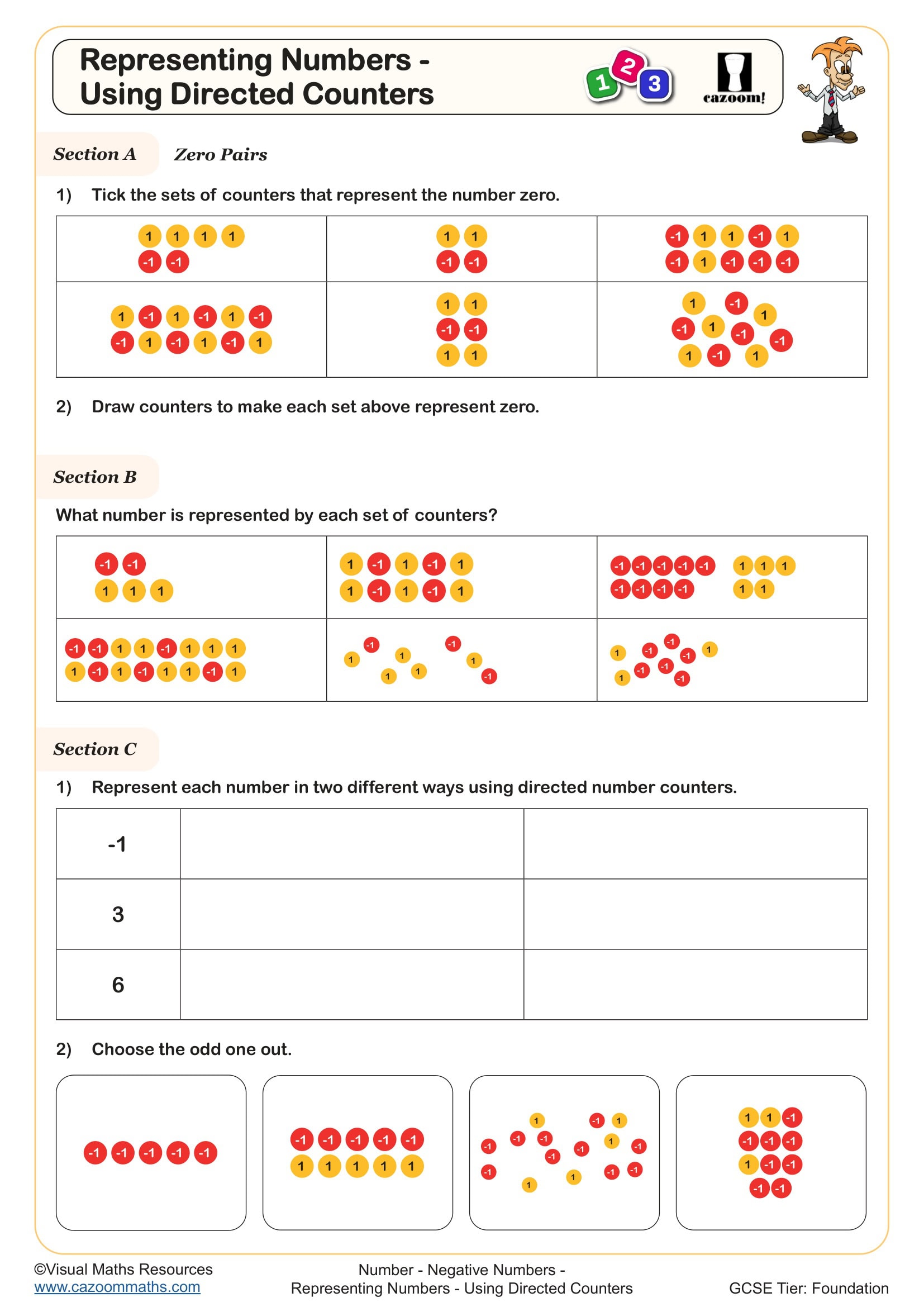
Directed number counters use physical or drawn representations to model positive and negative integers, typically with different colours representing each. Red counters commonly represent negative numbers whilst yellow or white counters represent positive numbers, allowing students to visualise operations by combining, removing, or grouping counters to demonstrate calculations.
The counter method proves particularly effective for multiplication because students can model repeated addition (for positive multipliers) or the removal of groups (for negative multipliers). A common error occurs when students try to rush to symbolic notation before understanding why three groups of negative two counters equals negative six, leading to procedural mistakes later. Teachers find that investing time in this concrete stage prevents misconceptions that persist into higher tiers at GCSE.
Which Year Groups Study Directed Number Counters?
These worksheets target Year 8 students within Key Stage 3, where directed number operations form a core component of the National Curriculum's Number strand. At this stage, students extend their understanding from simple addition and subtraction of integers to multiplication and division, with counter models providing scaffolding for these more complex operations.
By Year 8, students should be moving from concrete counter representations towards more abstract methods, though visual models remain valuable for checking understanding. The progression typically starts with addition and subtraction using counters in Year 7, advancing to multiplication in Year 8, before students tackle division and combined operations. This gradual shift from pictorial to abstract thinking aligns with how the curriculum builds algebraic reasoning skills needed for solving equations with negative coefficients.
Why Focus on Multiplication Using Counters Specifically?
Multiplication with directed numbers presents conceptual challenges that counters uniquely address by making the invisible visible. When students model 4 × (−3) using counters, they can physically create four groups of three negative counters, watching the result accumulate to −12. More importantly, counters help students grasp why (−3) × 4 produces the same result through commutativity, and why (−2) × (−3) equals positive 6 by modelling the removal of negative groups.
This understanding directly supports scientific contexts where students encounter rates of change in opposite directions. In physics, modelling velocity changes requires multiplying negative acceleration by time intervals, whilst in geography, temperature changes below zero follow multiplication patterns. Computer programming also relies on integer multiplication for coordinates moving in negative directions on screens, making this foundation essential for STEM progression beyond maths classrooms.
How Should Teachers Use These Directed Number Counter Worksheets?
The worksheets provide structured practice that moves students from drawing counter diagrams to interpreting them and finally connecting visual models to numerical calculations. This scaffolded approach works well when teachers model the first few examples with actual counters or coloured counters drawn on the board, then release students to complete worksheet exercises independently or in pairs.
These resources suit multiple classroom contexts beyond standard lessons. Teachers use them effectively for intervention sessions with students who've missed foundational integer understanding, as homework to consolidate visual methods before introducing abstract rules, or as starter activities to diagnose whether students truly grasp why multiplication rules work. The complete answer sheets enable students to self-assess their diagram accuracy and numerical answers, whilst paired work encourages mathematical discussion about why certain counter arrangements produce specific results.