Year 8 Number Lines Worksheets
All worksheets are created by the team of experienced teachers at Cazoom Maths.
Why are number lines still important in Year 8?
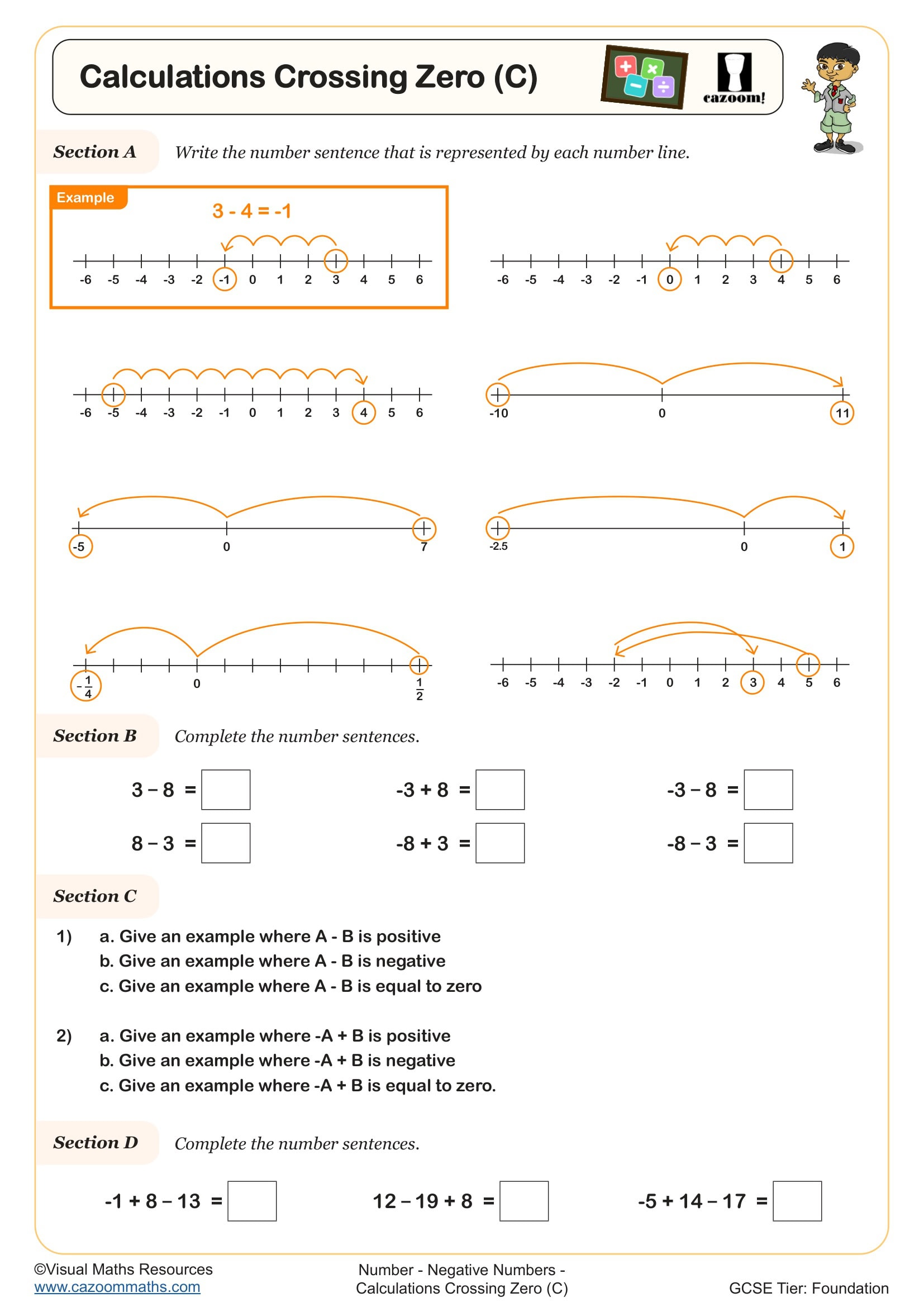
Number lines remain a powerful tool in Year 8 because they provide a visual model for increasingly abstract concepts, particularly when working with negative numbers, decimals, and later algebraic thinking. While Year 8 students may view them as primary school methods, number lines help bridge the gap between concrete arithmetic and the more formal algebraic methods introduced at KS3.
Teachers often observe that students who dismiss number lines as 'too basic' struggle more with directed numbers and inequalities later in the year. The visual representation helps students understand why subtracting a negative number means moving right, or why multiplying by a negative reverses direction. Encouraging Year 8 students to use number lines strategically, rather than abandoning them entirely, supports deeper mathematical understanding and provides a reliable checking method for exam questions.
Which year groups use number lines in KS3?
These resources are designed specifically for Year 8, where number lines extend beyond basic counting and simple addition to include decimal operations, exchanges, and more sophisticated problem-solving applications. At KS3, the National Curriculum expects students to use number lines flexibly as one of several methods for calculations and for representing mathematical relationships.
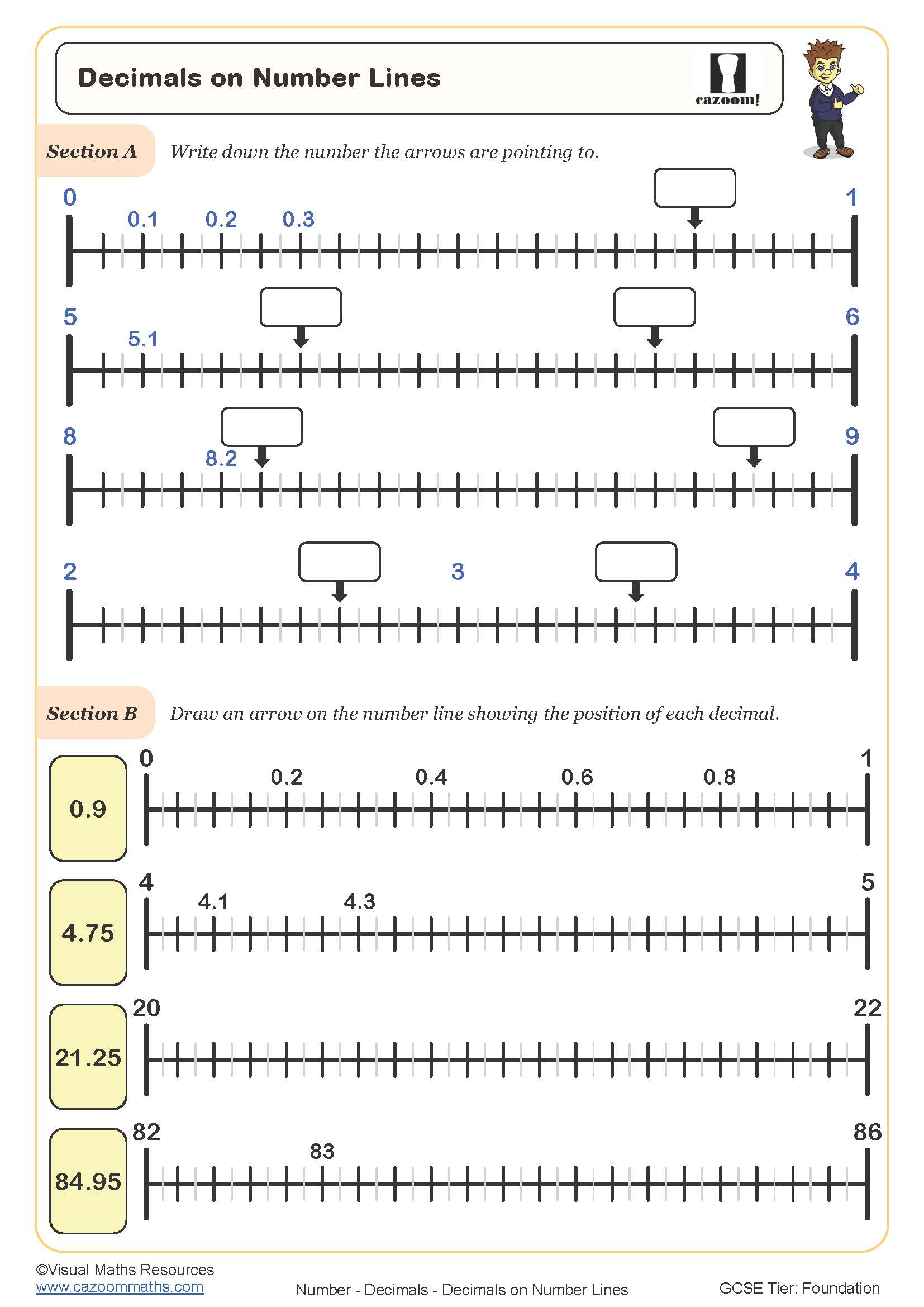
The progression from Year 7 to Year 8 shifts from consolidating whole number and basic decimal work towards more complex decimal subtraction and understanding exchanges across place values. Year 8 students should be using number lines to model problems involving tenths and hundredths with precision, and beginning to see connections between number line representations and the coordinate systems they'll encounter in algebra and graphs.
How do students subtract decimals using number lines?
Subtracting decimals on a number line involves marking the starting number, then counting back in steps that match the decimal structure being subtracted. Students might work with jumps of whole numbers first, then tenths, then hundredths, or combine these strategically. The number line makes the process of exchanging between place values visible, showing why borrowing is necessary in column methods.
This skill has direct applications in measurement and finance. Scientists use number lines when calculating differences in temperature readings that include decimal places, whilst engineers use similar visual methods when working with tolerances and measurements. Understanding decimal subtraction through number lines helps students grasp why a temperature drop from 3.7°C to -1.2°C represents a change of 4.9°C, a calculation pattern they'll encounter in science investigations and real data analysis throughout their education.
How can teachers use these number line worksheets effectively?
The worksheets provide structured practice that moves from guided examples through to independent problem-solving, allowing students to build confidence with decimal positioning and calculation strategies. The variety of questions helps students recognise when number lines are the most efficient method and when alternative approaches might be quicker, developing their mathematical reasoning alongside procedural fluency.
Many teachers use these resources during intervention sessions for students who struggle with decimal column methods, as the visual approach often clarifies where errors occur. They work well as homework to reinforce classroom teaching, or as starter activities to assess understanding before moving to more complex decimal operations. The complete answer sheets allow for self-assessment during paired work, which helps students identify their own misconceptions about place value and exchanges without waiting for teacher marking.