Year 8 Powers and Roots Worksheets
Add and Subtract in Standard Form

Calculating Using Standard Form

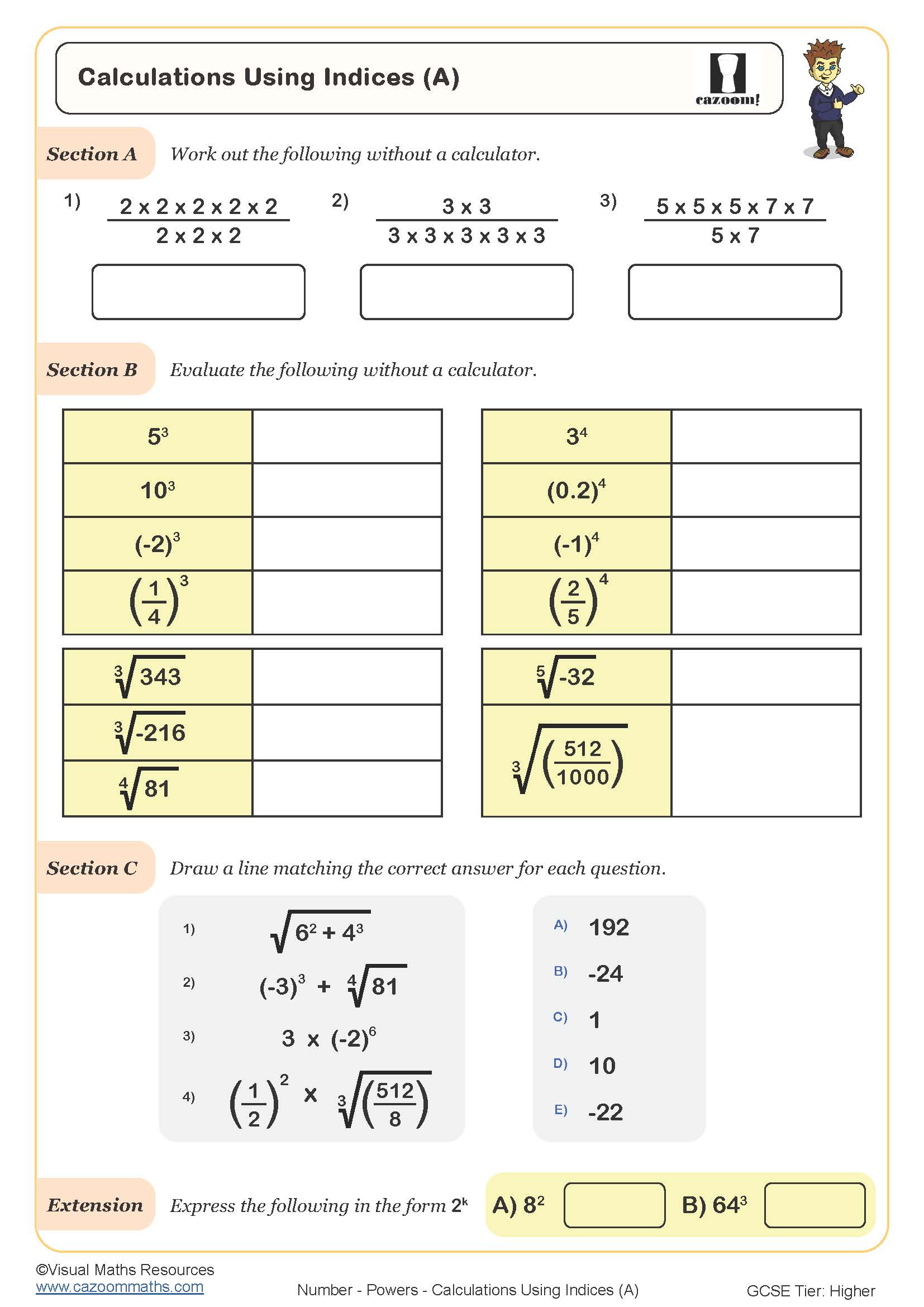
Calculations Using Indices (A)
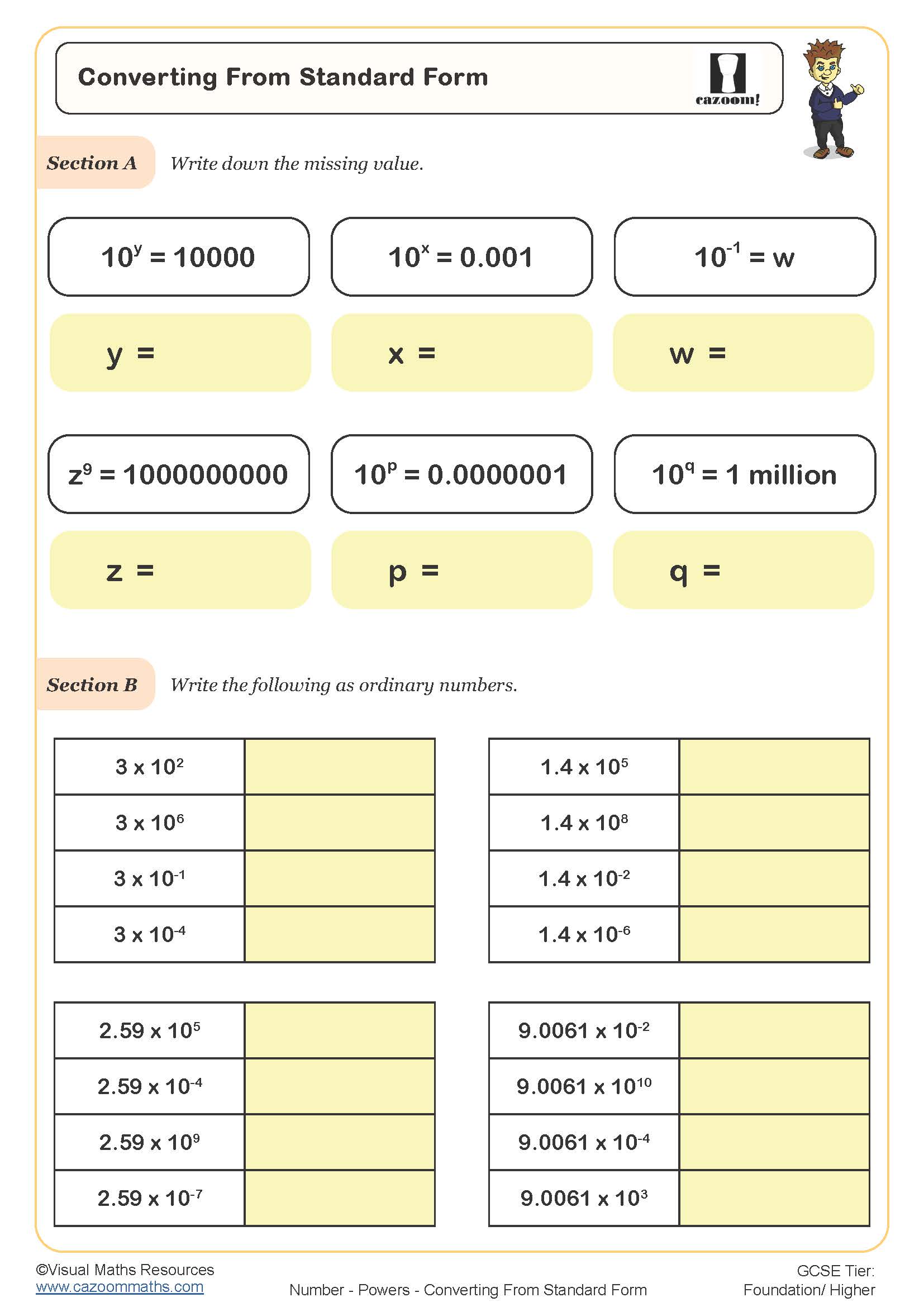
Converting from Standard Form
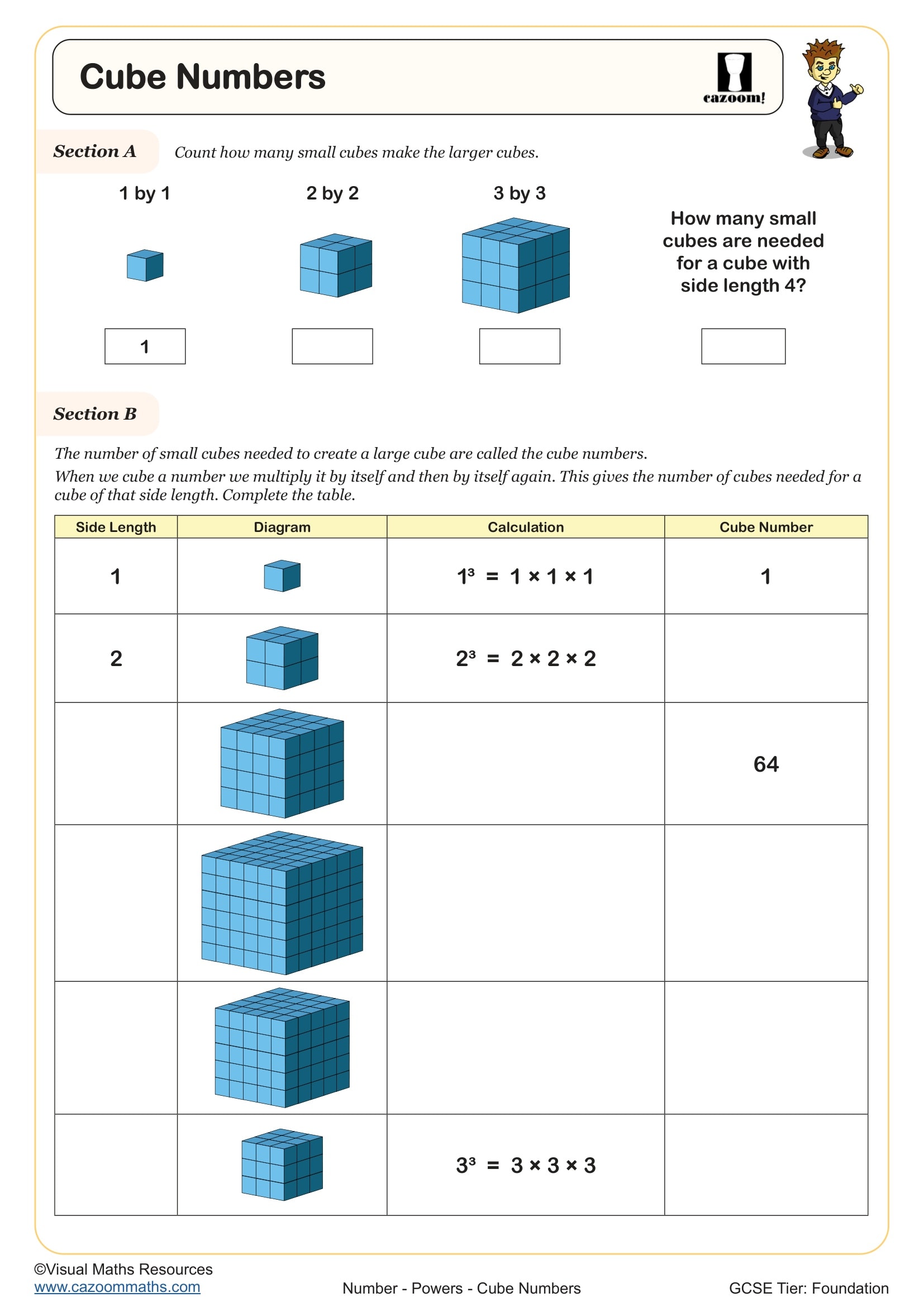
Cube Numbers
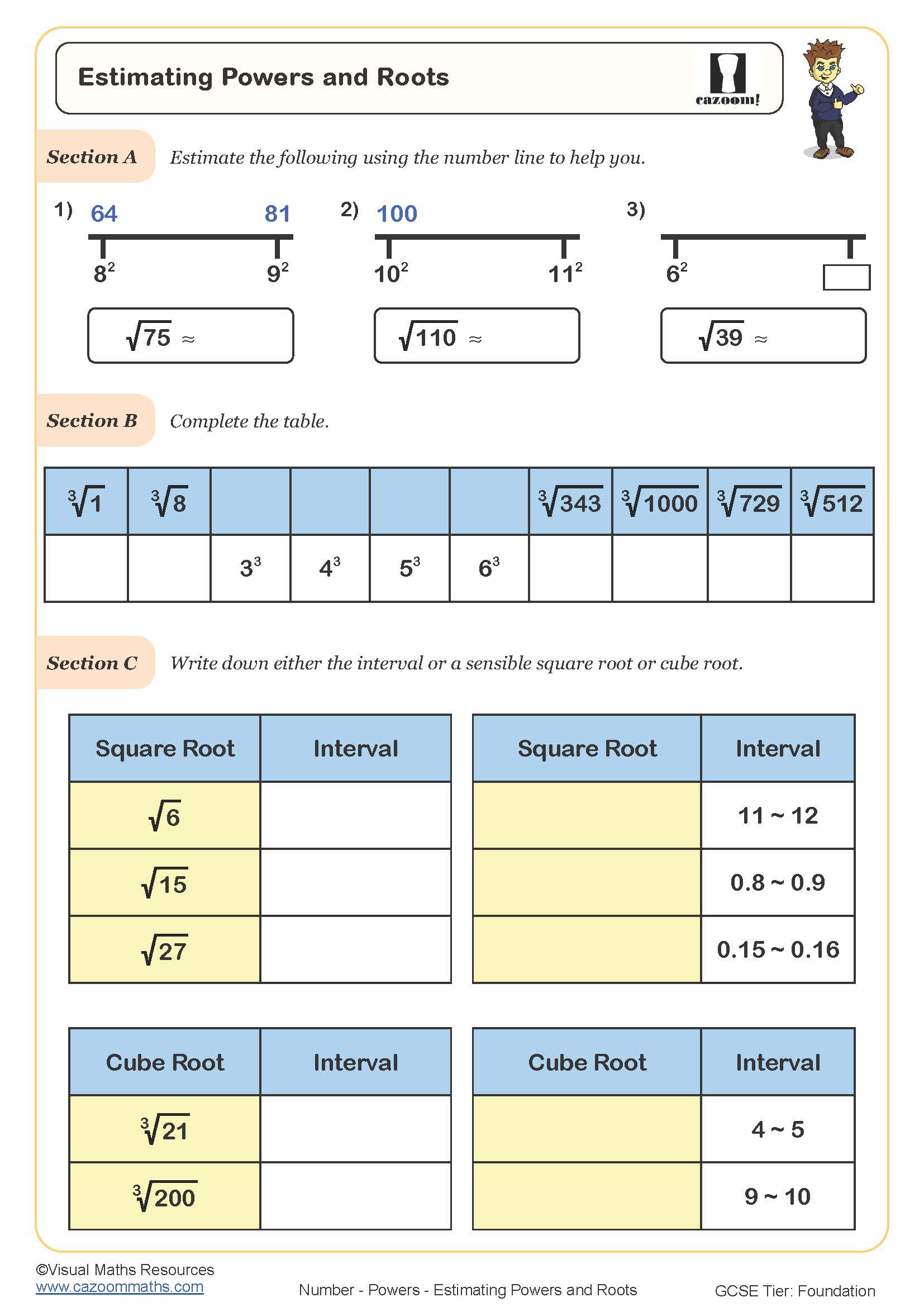
Estimating Powers and Roots
Estimating Square Roots

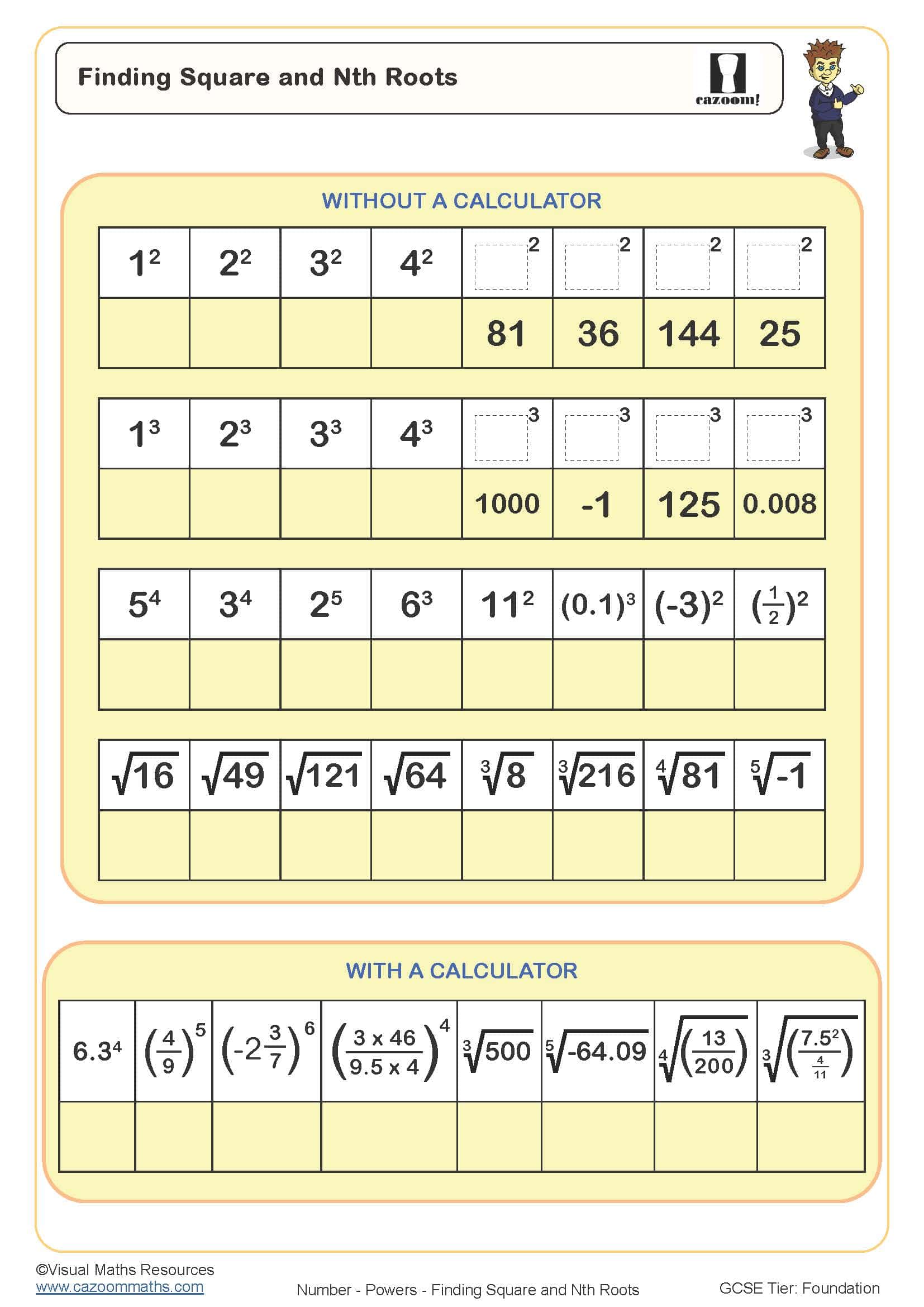
Finding Square and Nth Roots
Manipulating Standard Form (B)

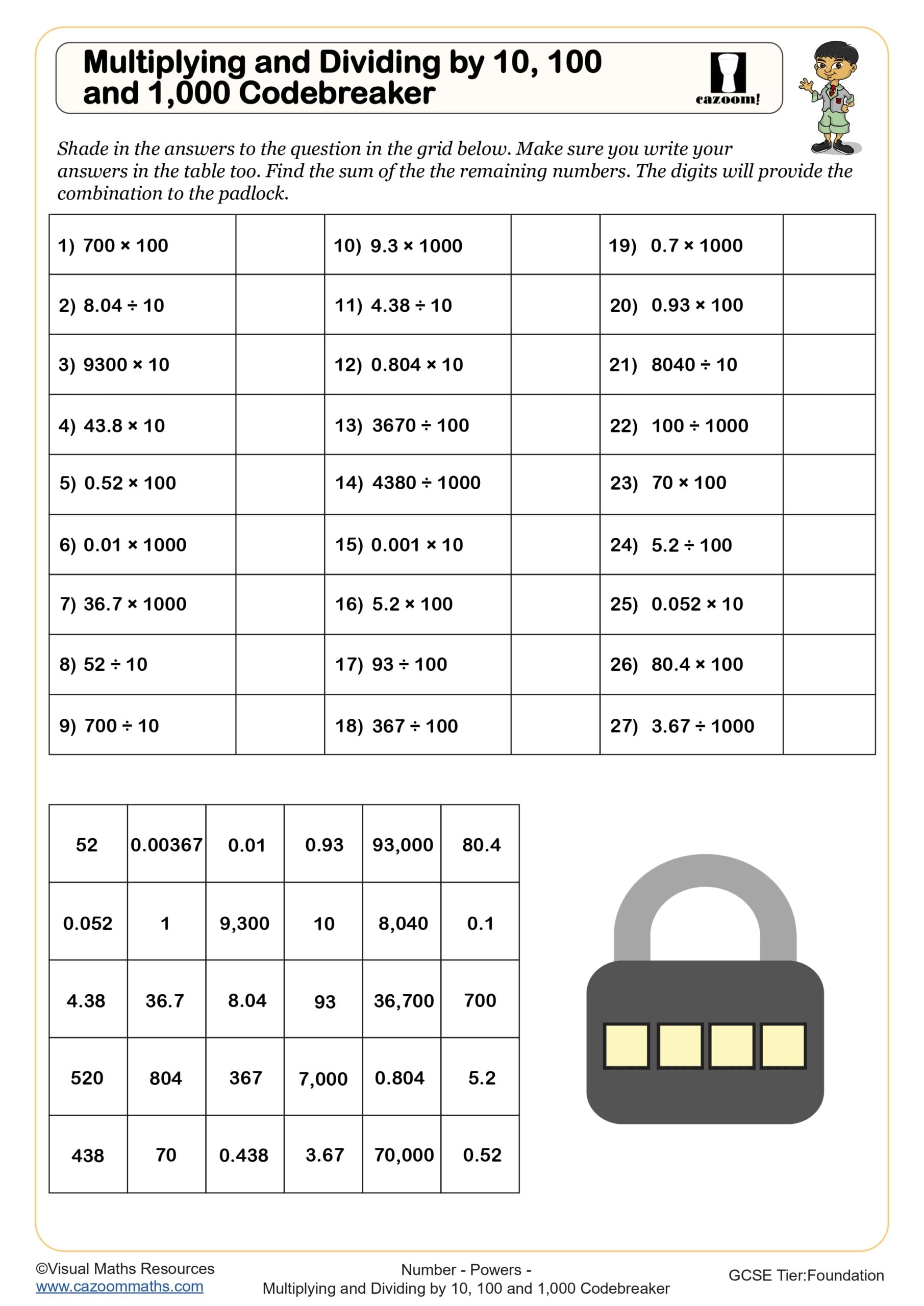
Multiplying and Dividing by 10, 100 and 1,000 Codebreaker
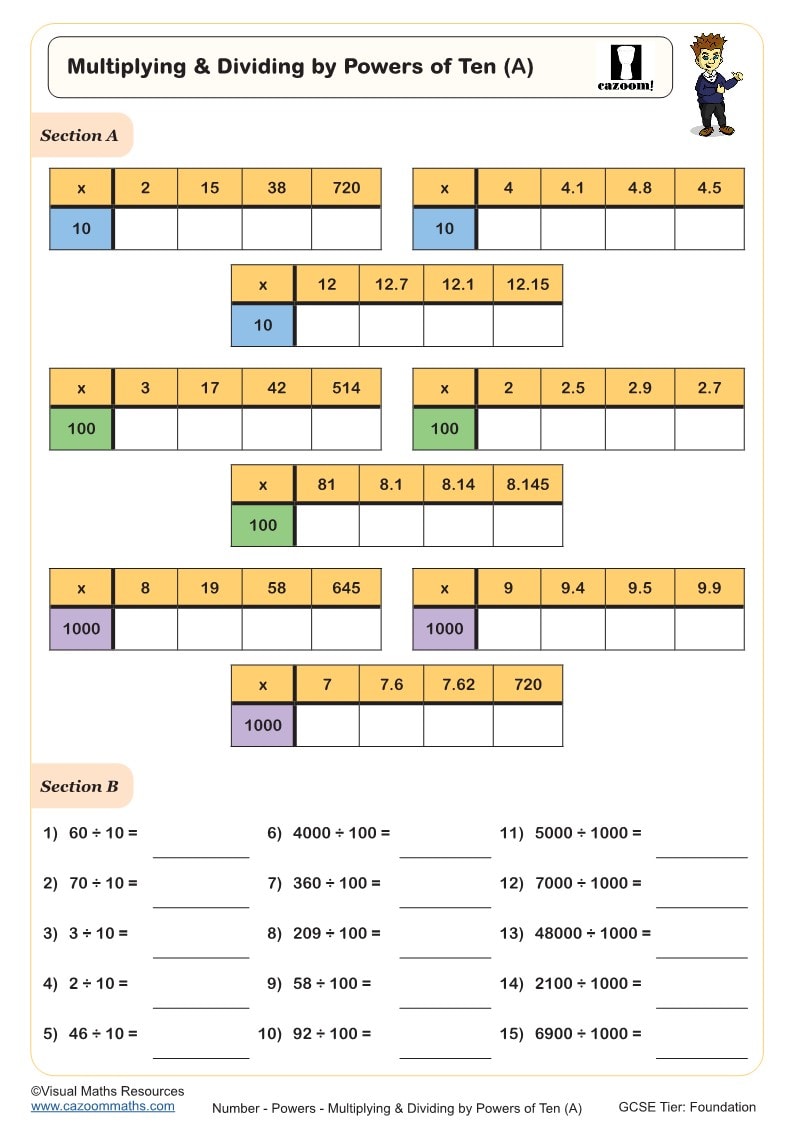
Multiplying and Dividing by Powers of Ten (A)
Multiplying and Dividing by Powers of Ten (B)

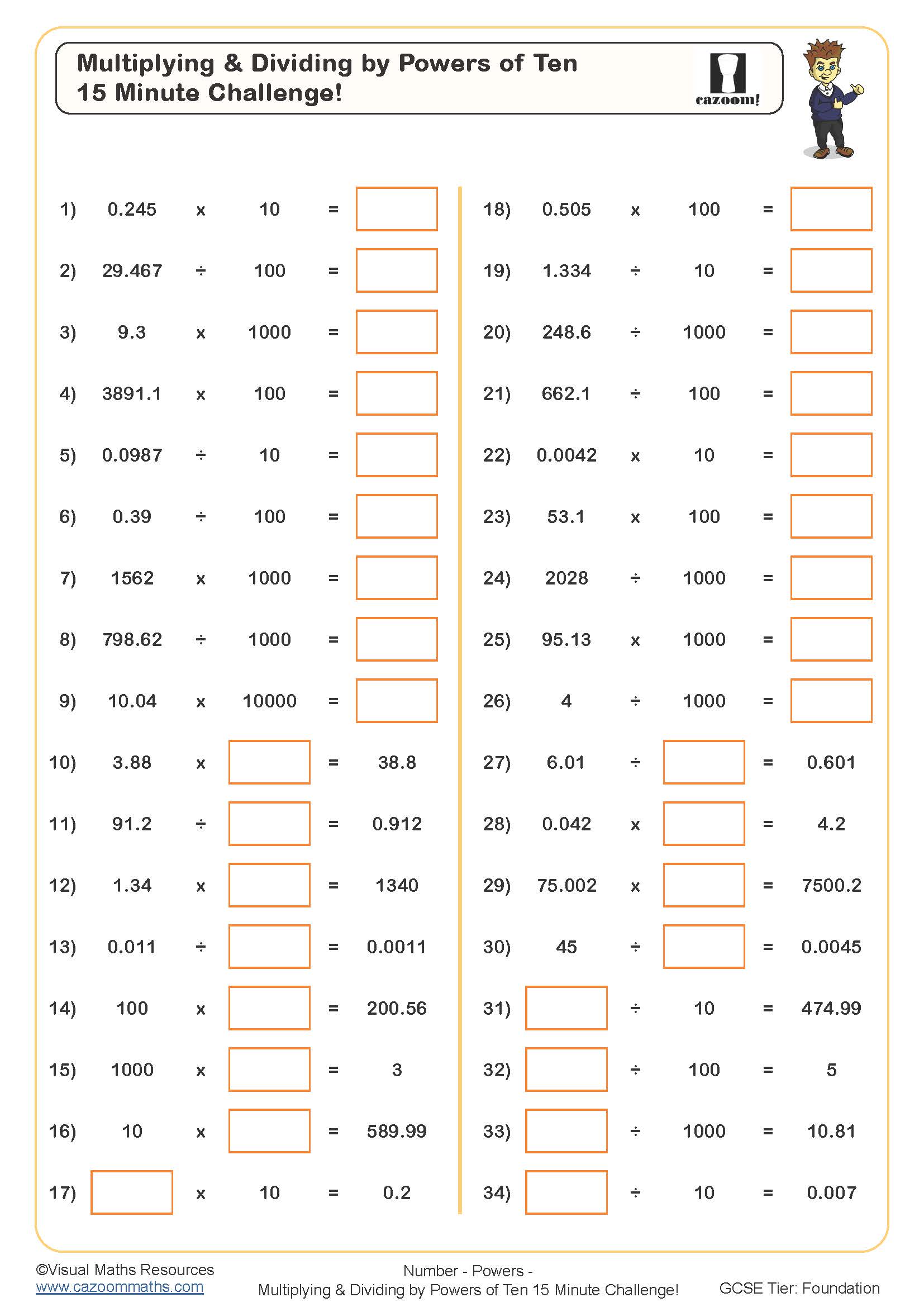
Multiplying and Dividing by Powers of Ten 15 Minute Challenge
Multiplying and Dividing by Ten

Powers of Ten Problem Solving
Recognising Standard Form

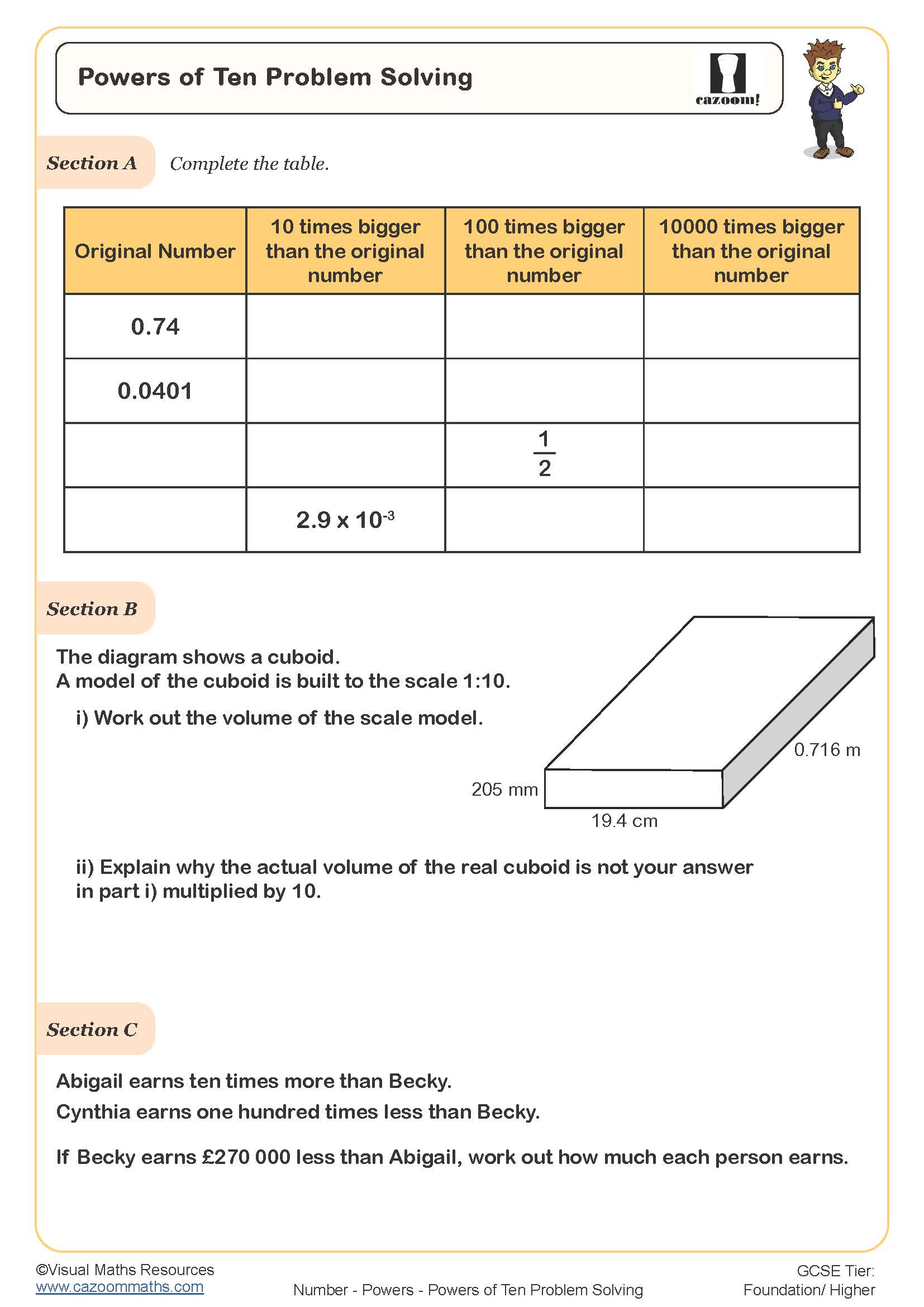
Spotting Standard Form
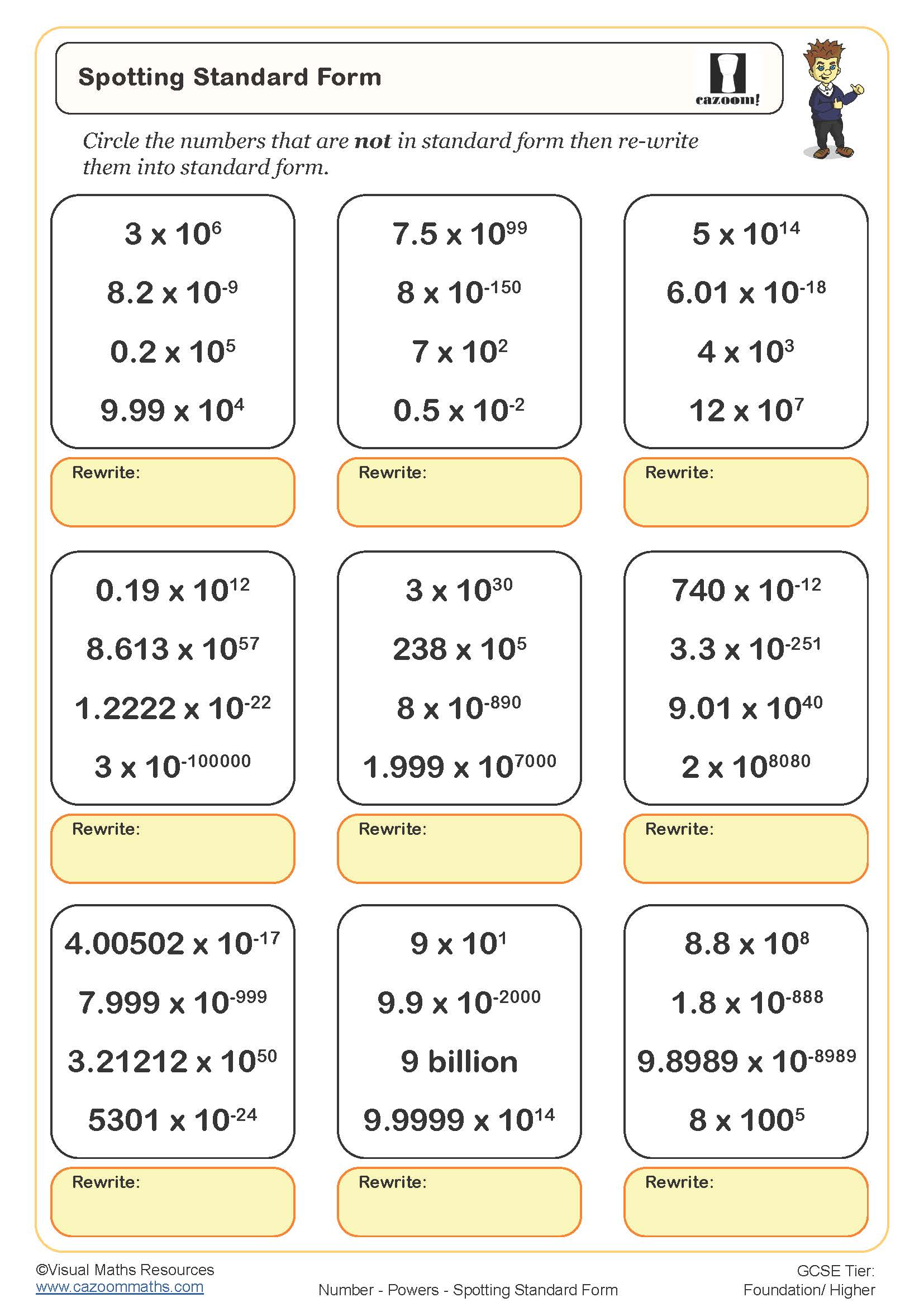
Square Numbers
Square Numbers, Cube Numbers and Other Powers

Standard Form (A)
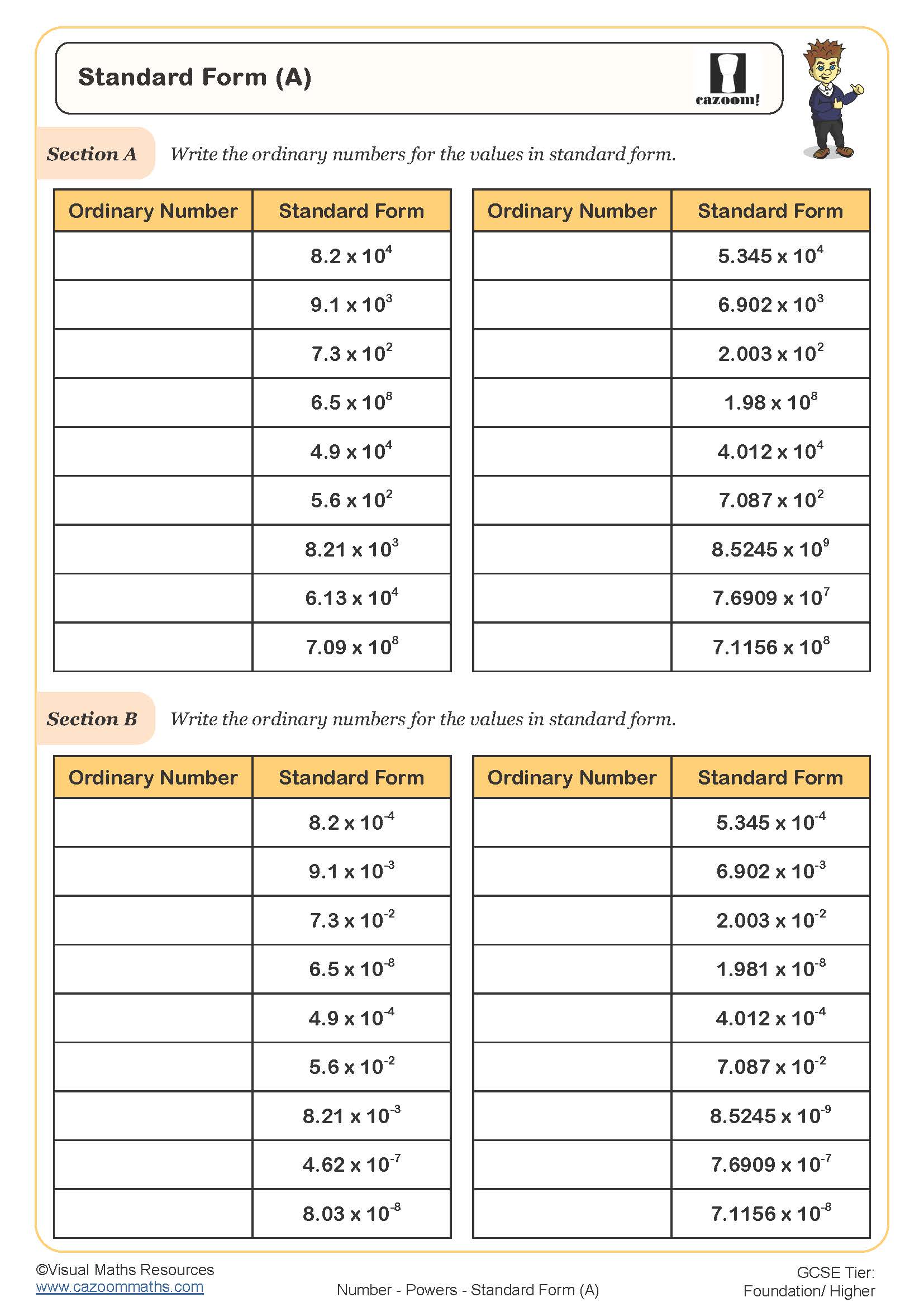
Standard Form (B)
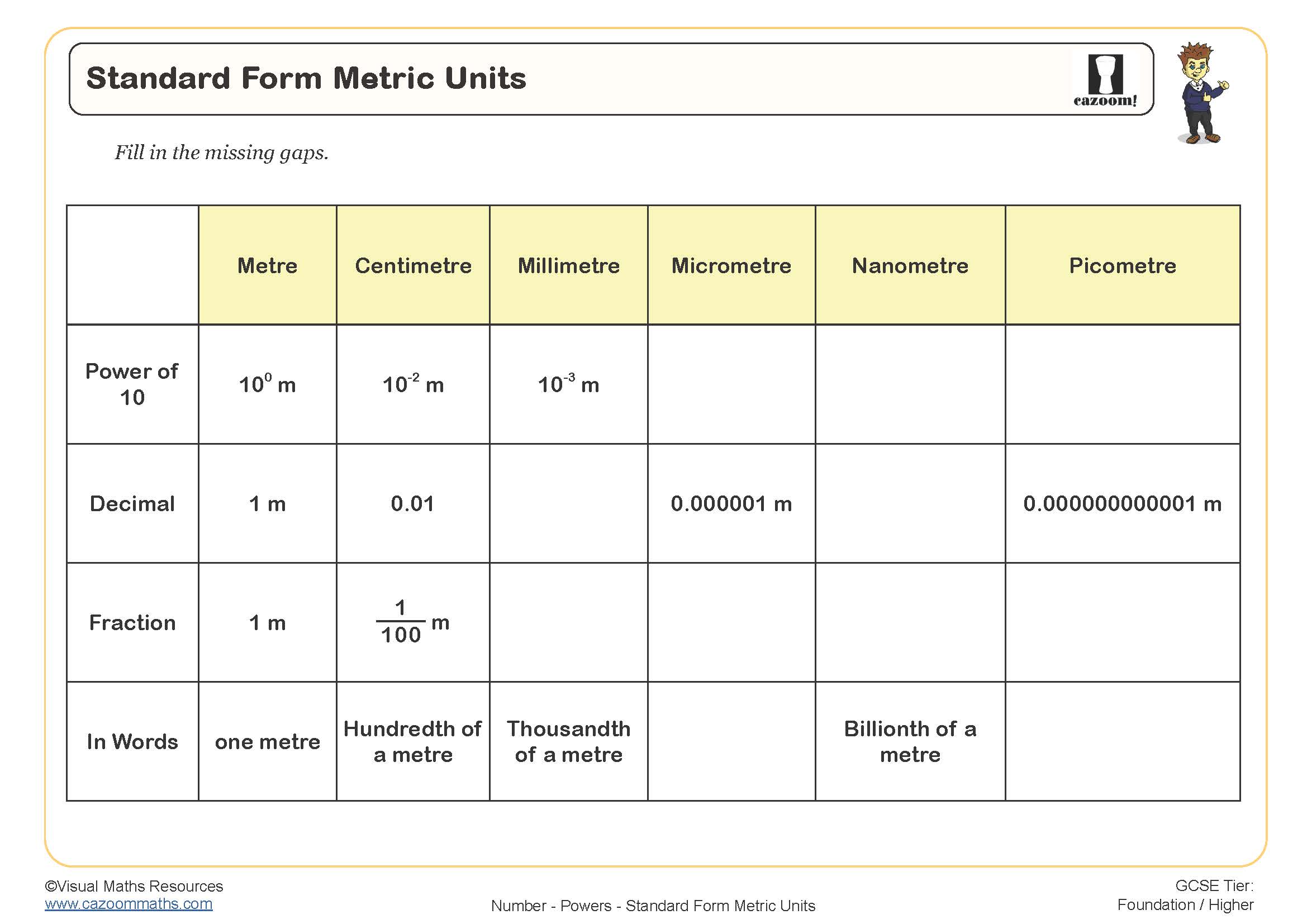
Standard Form Metric Units
Standard Form Problem Solving

All worksheets are created by the team of experienced teachers at Cazoom Maths.
7 Benefits of Using Printable Year 8 Number Activities in Class and at Home
These resources mark a crucial transition in algebraic understanding, moving students from arithmetic operations to recognising exponential patterns that underpin higher mathematics. The process of learning index laws enables students to develop logical reasoning abilities because they learn how powers combine through multiplication of exponents and separate through division of exponents. The transition from memorisation of rules to understanding mathematical structure enables students to become independent thinkers who can solve new problems. Students who practice different question types develop mental flexibility because they learn to move between multiple representations of mathematical concepts. The systematic progression prevents knowledge gaps that often emerge in later years when encountering logarithms or complex scientific calculations.
Specific learning benefits include:
• Master the multiplication and division of indices
• Develops understanding of negative powers
• Strengthens algebraic manipulation skills
• Connects roots to fractional indices
• Recognises patterns in exponential growth
• Prepares for GCSE standard form
• Enhances scientific calculation abilities
Cazoom Maths Worksheets: Complete Powers and Roots Topic Coverage at a Glance
These worksheets progress methodically from concrete numerical examples through pictorial representations to abstract algebraic forms, ensuring deep conceptual understanding. Each resource includes detailed worked solutions showing step-by-step reasoning. Visual representations support different learning styles whilst maintaining mathematical rigour throughout the collection.
The worksheets in this collection include:
• Introduction to Index Notation — explores writing repeated multiplication using powers
• Multiplying Powers — practices combining terms with the same base
• Dividing Powers — develops skills in simplifying exponential divisions
• Power of a Power — strengthens understanding of nested exponents
• Negative Indices — introduces reciprocals through negative exponents
• Fractional Indices — connects roots to fractional power notation
• Mixed Index Problems — combines multiple index laws in a single question
• Algebraic Indices — extends index rules to algebraic expressions
Why Teachers Choose These Time-Saving Powers and Roots Resources
Horizontal and vertical differentiation within each worksheet eliminates the need for multiple resource sets, allowing seamless adaptation to mixed-ability classrooms. The uniform structure in all materials decreases instructional time because students learn the layout and expectations. The presentation of work solutions enables instructors to observe student thought processes, which makes grading serve as a diagnostic tool to detect particular errors in understanding. Teachers can determine proper starting points for students through clear progression markers without needing extensive pre-assessment. The resources fit seamlessly into current lesson plans for teaching, consolidation work, homework tasks and targeted intervention activities. The visual design reduces cognitive overload, which benefits students who have difficulty with dense text or complex instructions.
Real-World Applications Where Year 8 Students Encounter Powers Daily
Understanding exponential relationships prepares students for careers in science, technology, engineering and finance, where powers form the language of measurement and growth.
• Computing storage sizes in technology devices and cloud systems
• Understanding earthquake intensity through Richter scale measurements
• Calculating compound interest for savings accounts and investments
• Measuring astronomical distances between planets and stars
• Analysing population growth rates and epidemic spread patterns
• Working with area and volume in construction projects
• Interpreting pH scales in chemistry and environmental science
• Understanding sound intensity measured in decibels