Year 8 Rounding Worksheets
Approximation (A)
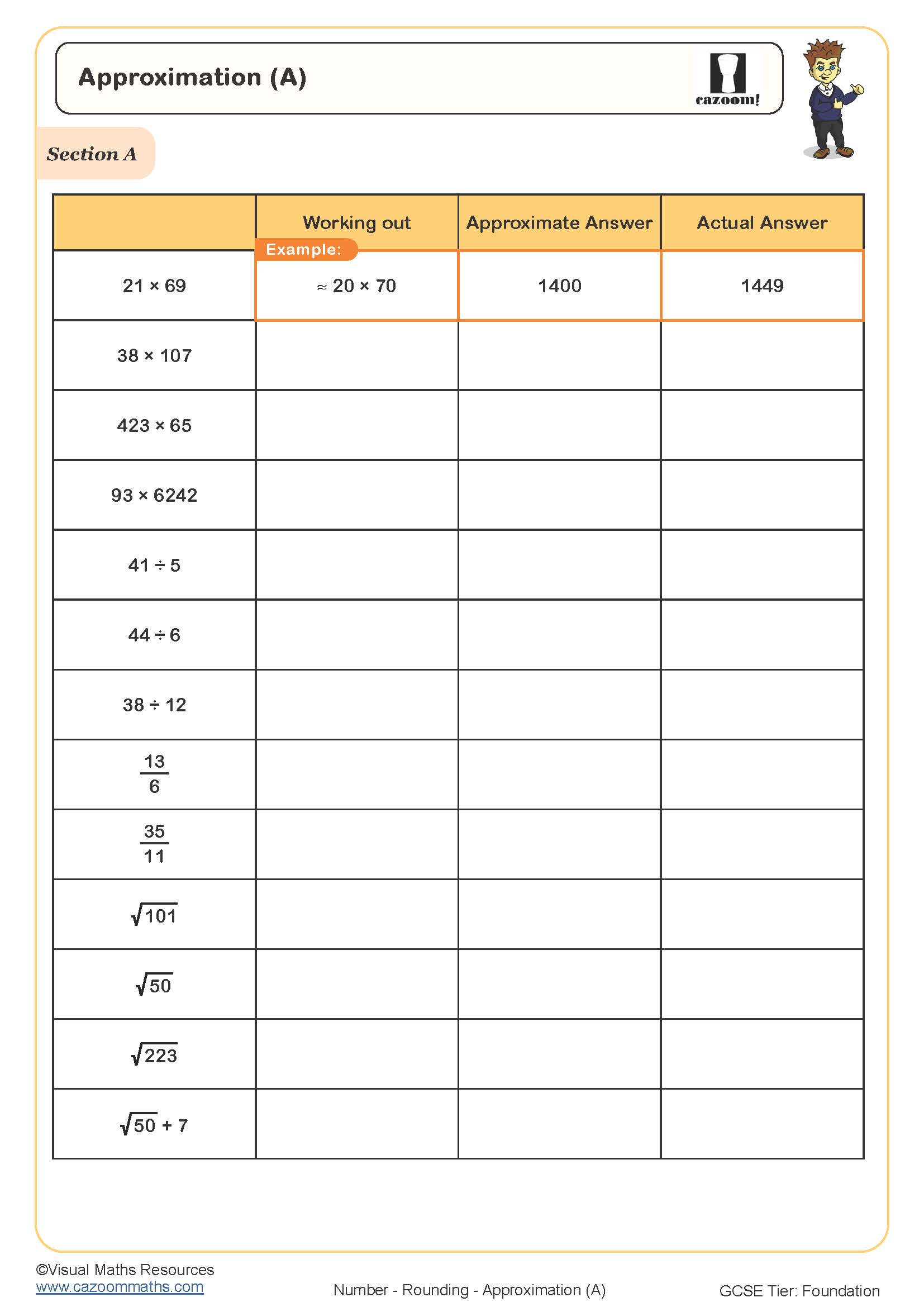
Approximation (B)
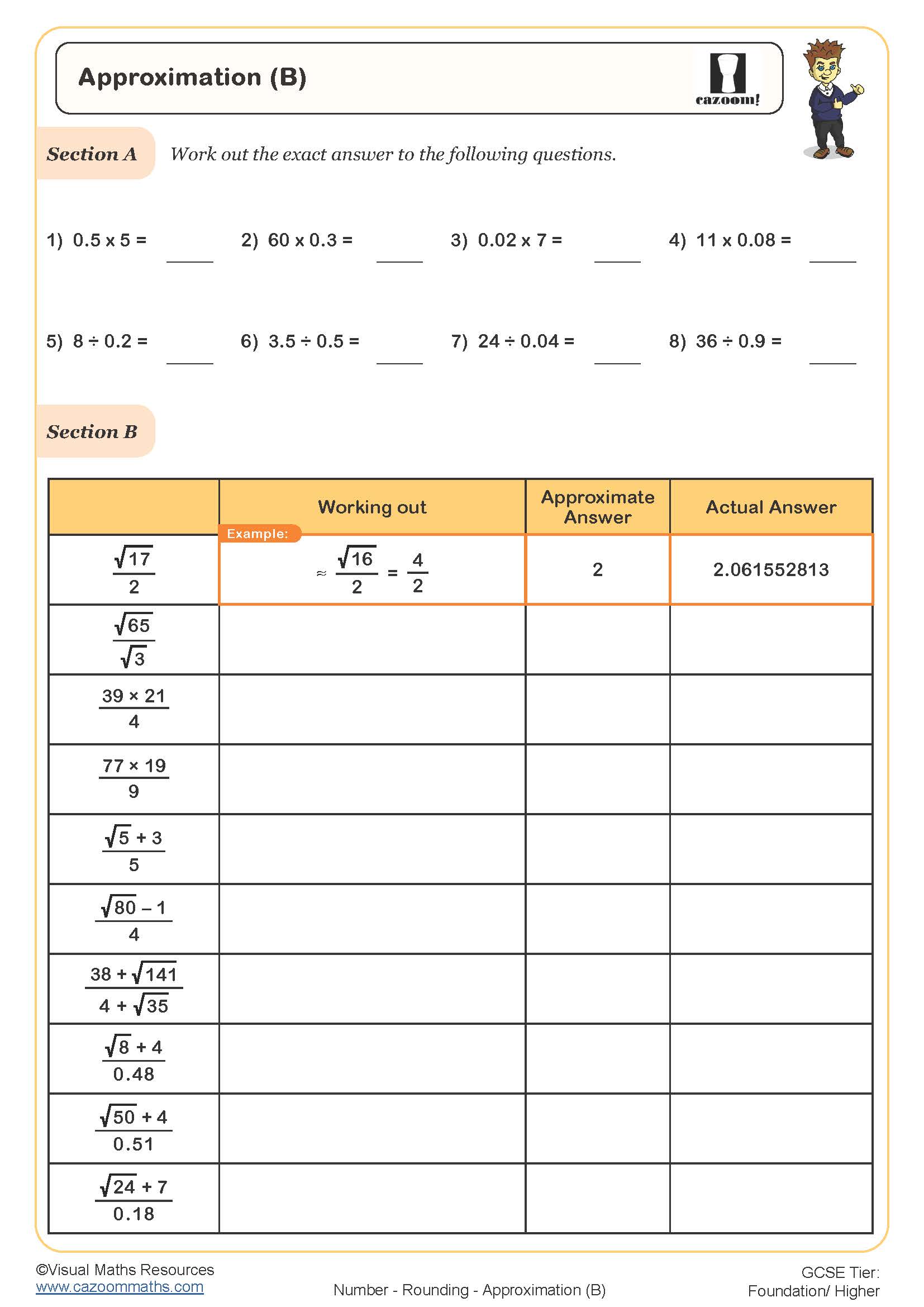
Estimating Powers and Roots
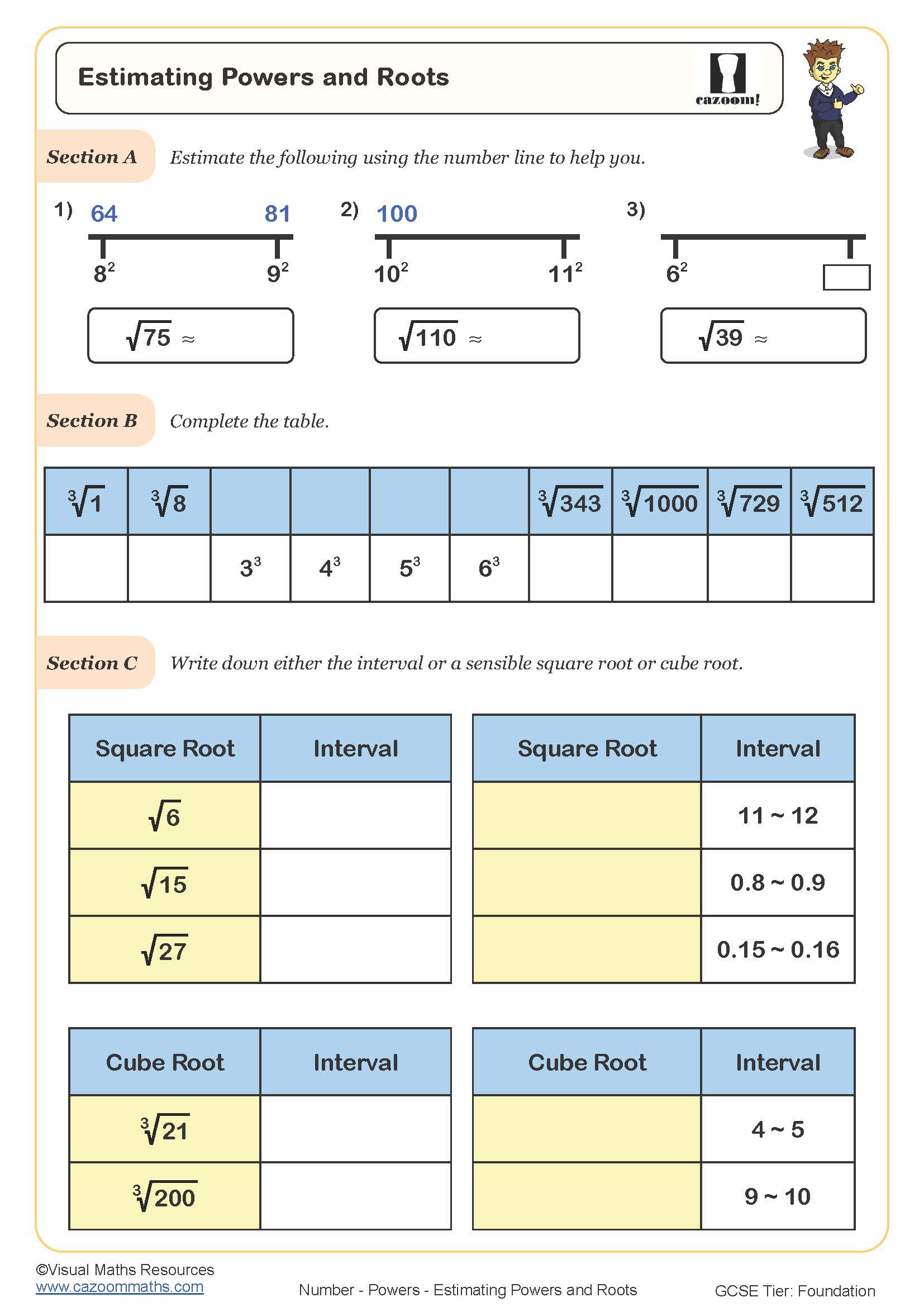
Rounding Charts
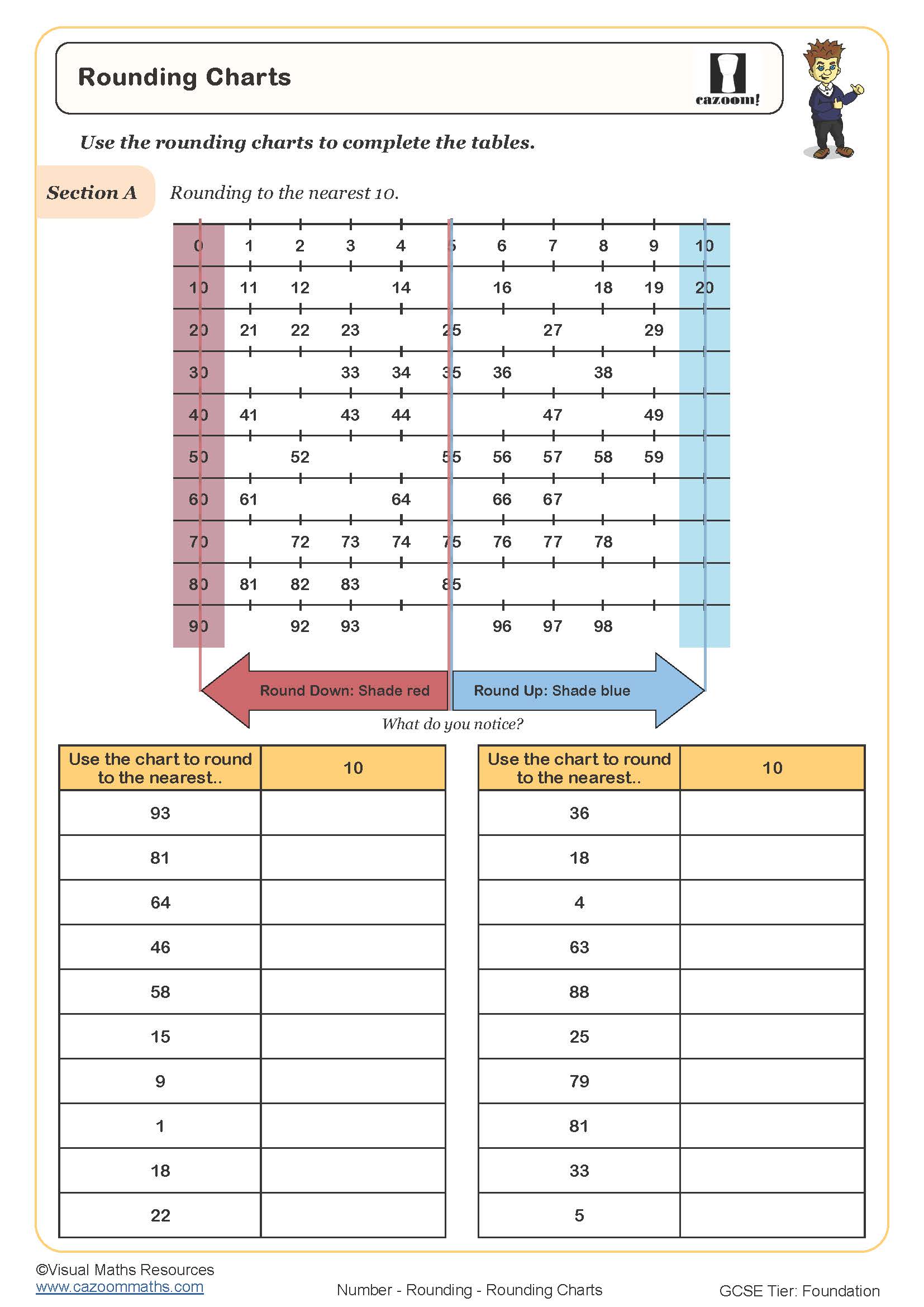
Rounding Mixed Exercise

Rounding to Decimal Places
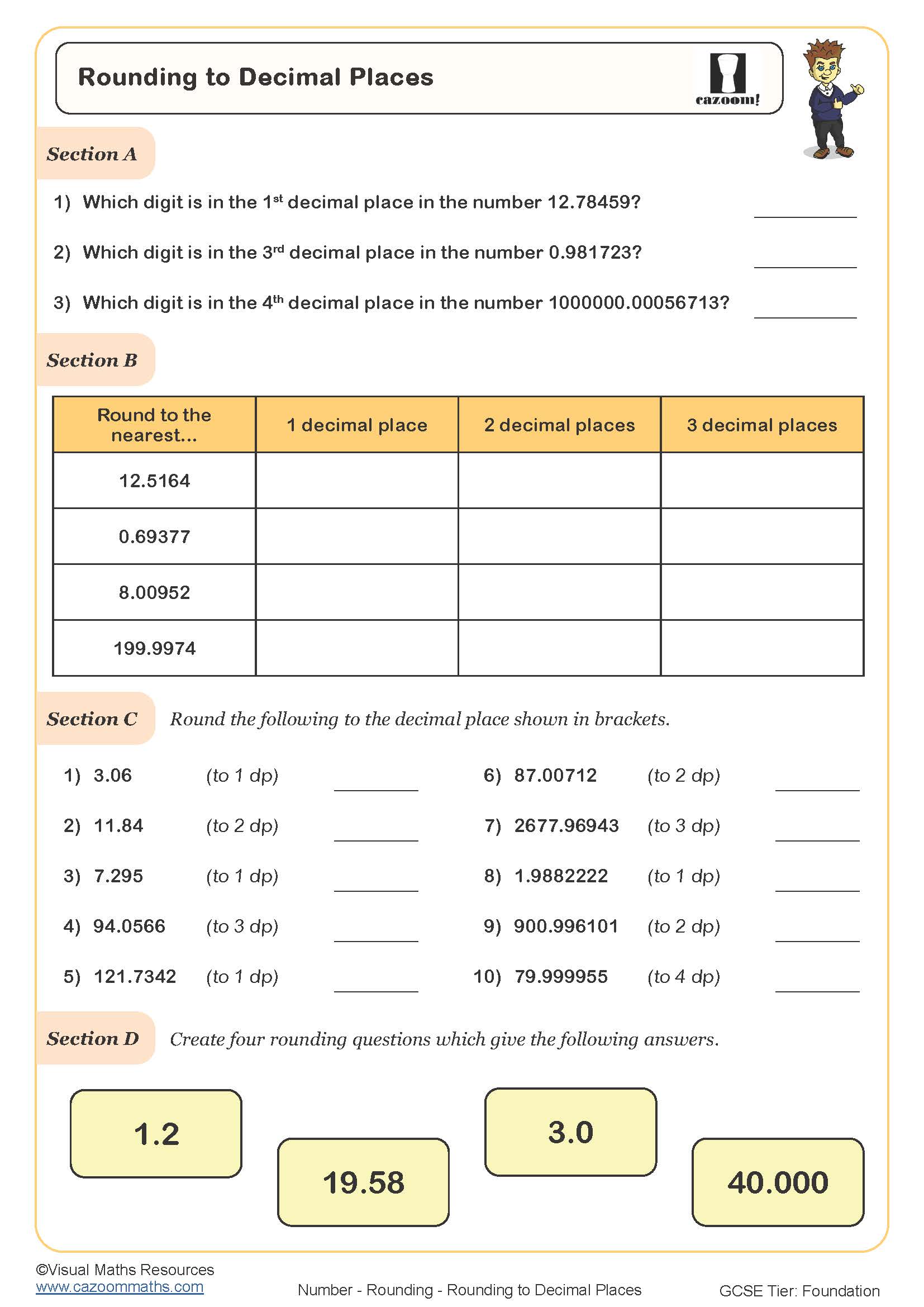
Rounding to One Decimal Place
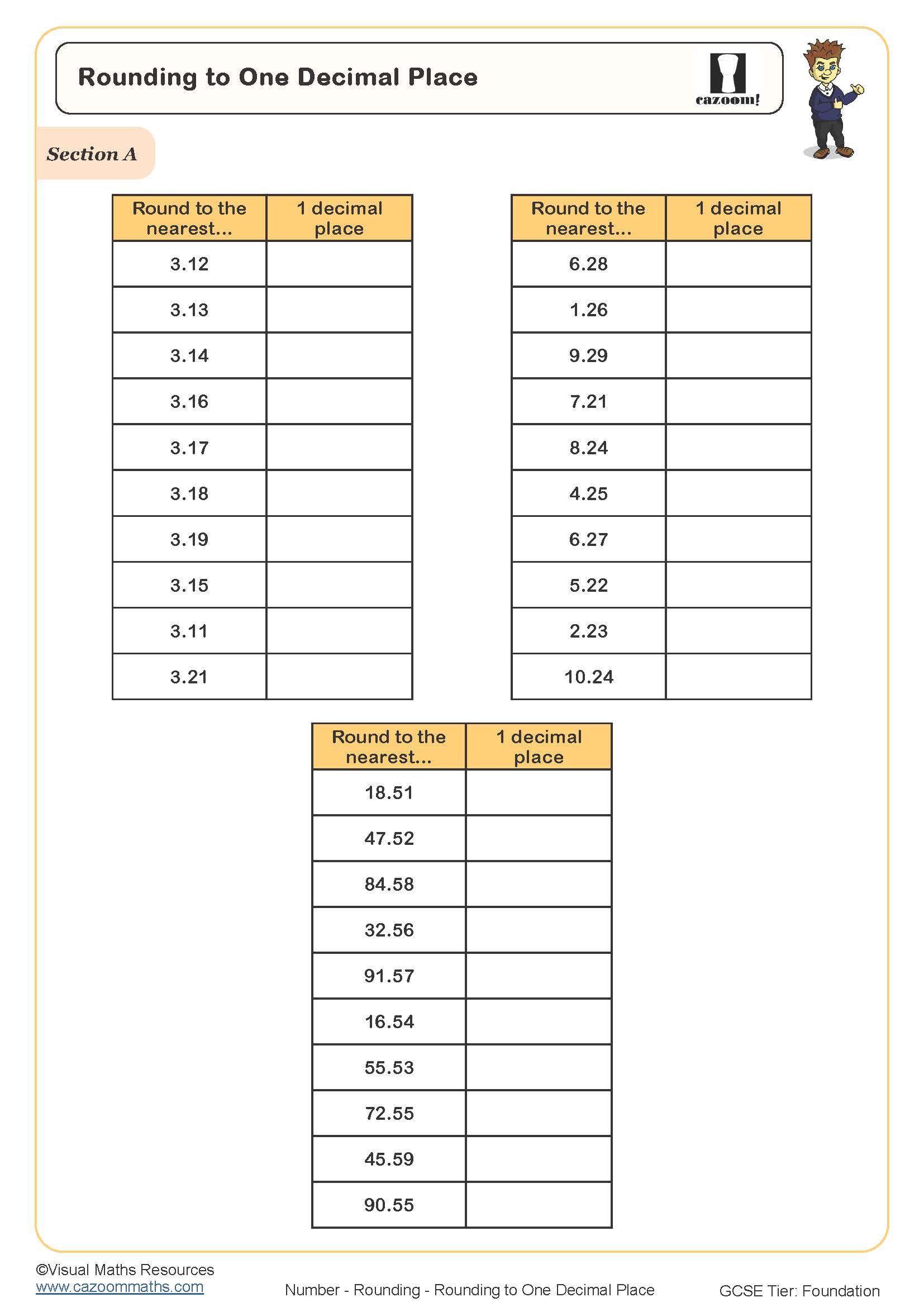
Rounding to the Nearest Hundred
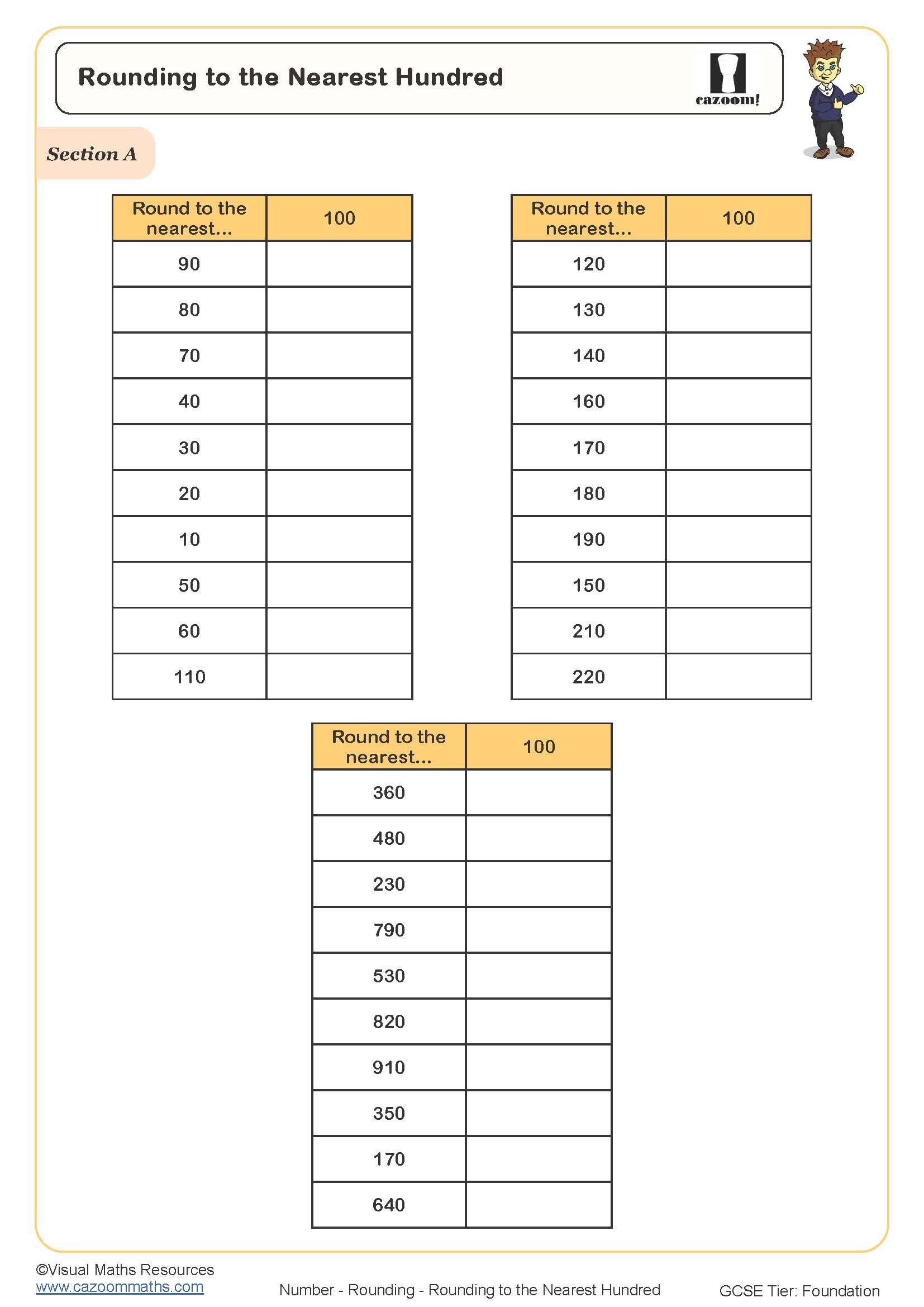
Rounding to the Nearest Ten
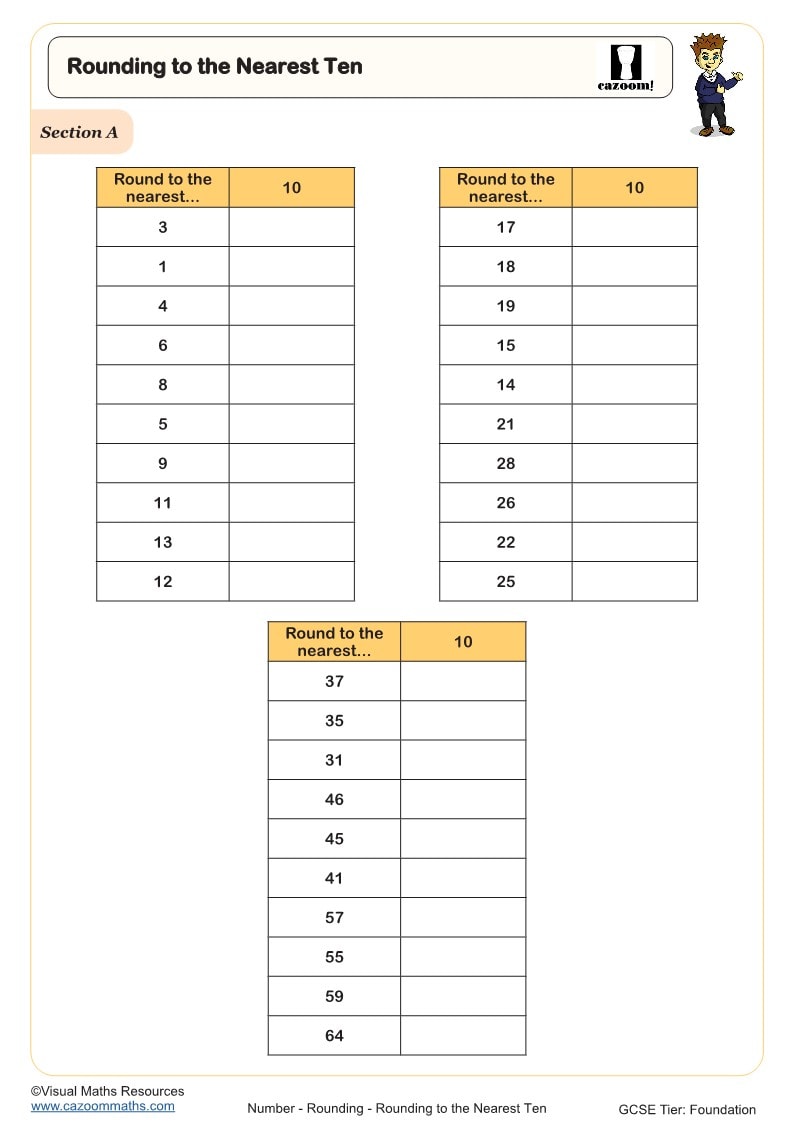
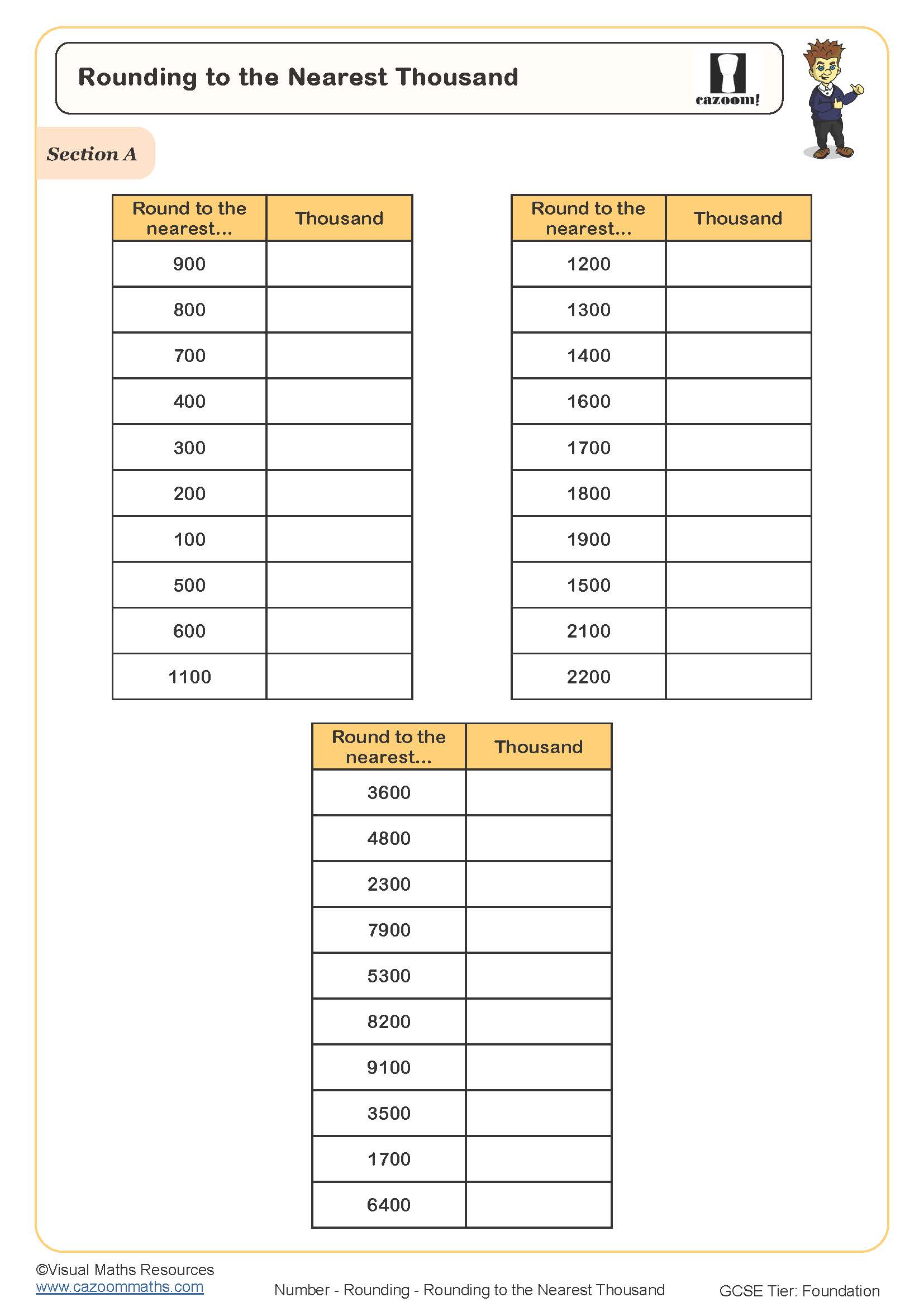
Rounding to the Nearest Thousand
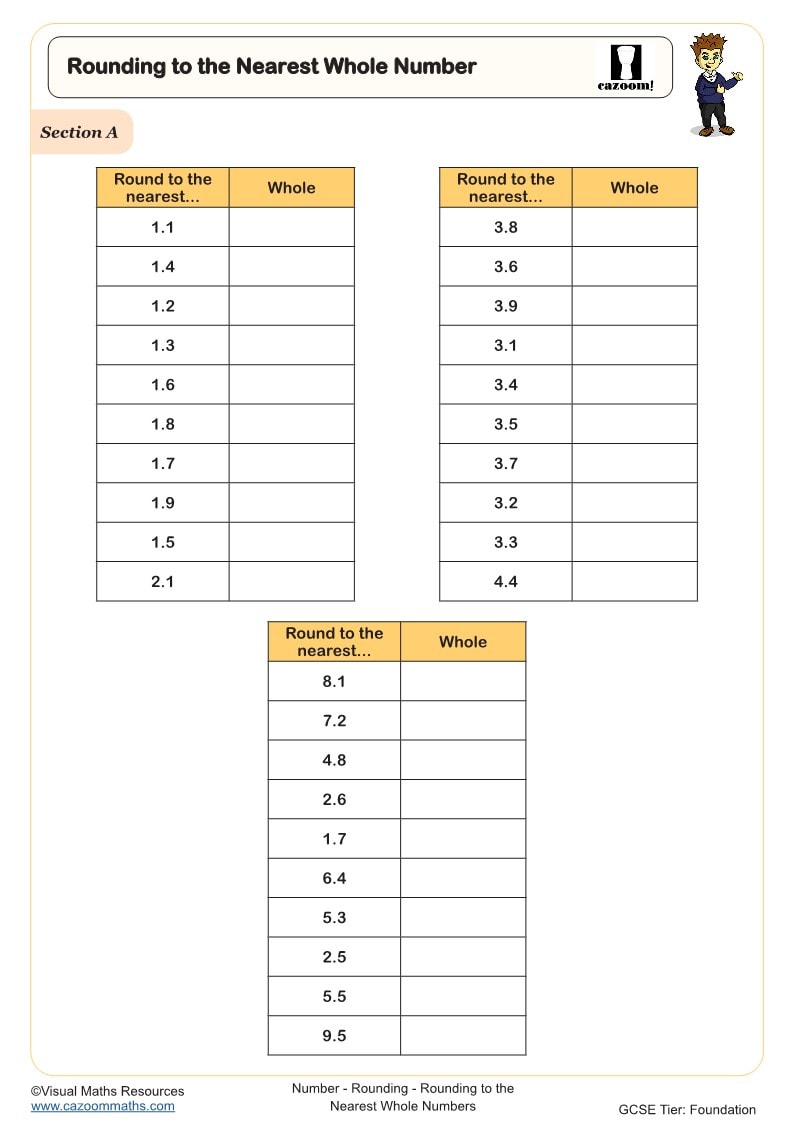
Rounding to the Nearest Whole Number
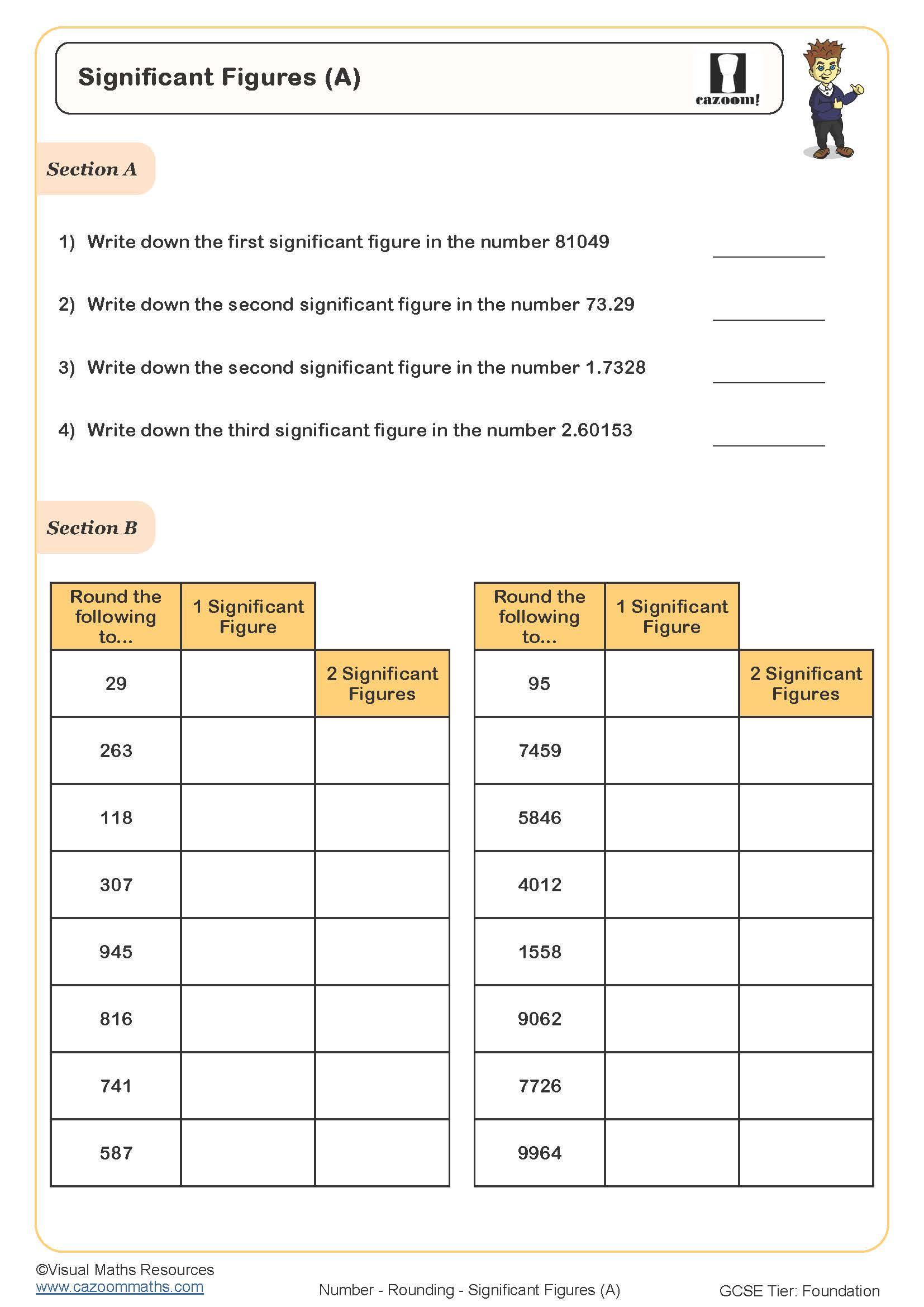
Significant Figures (A)
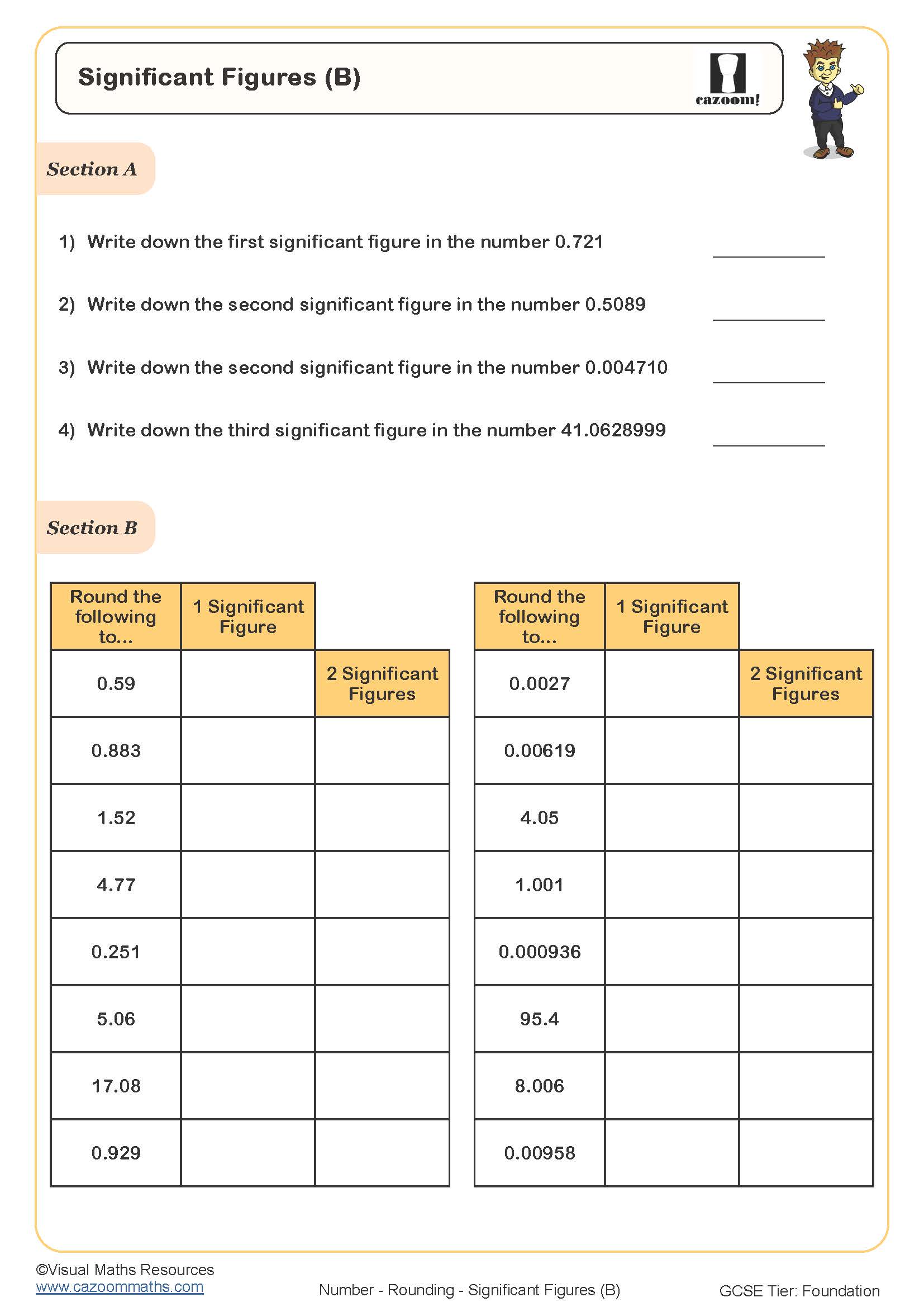
Significant Figures (B)
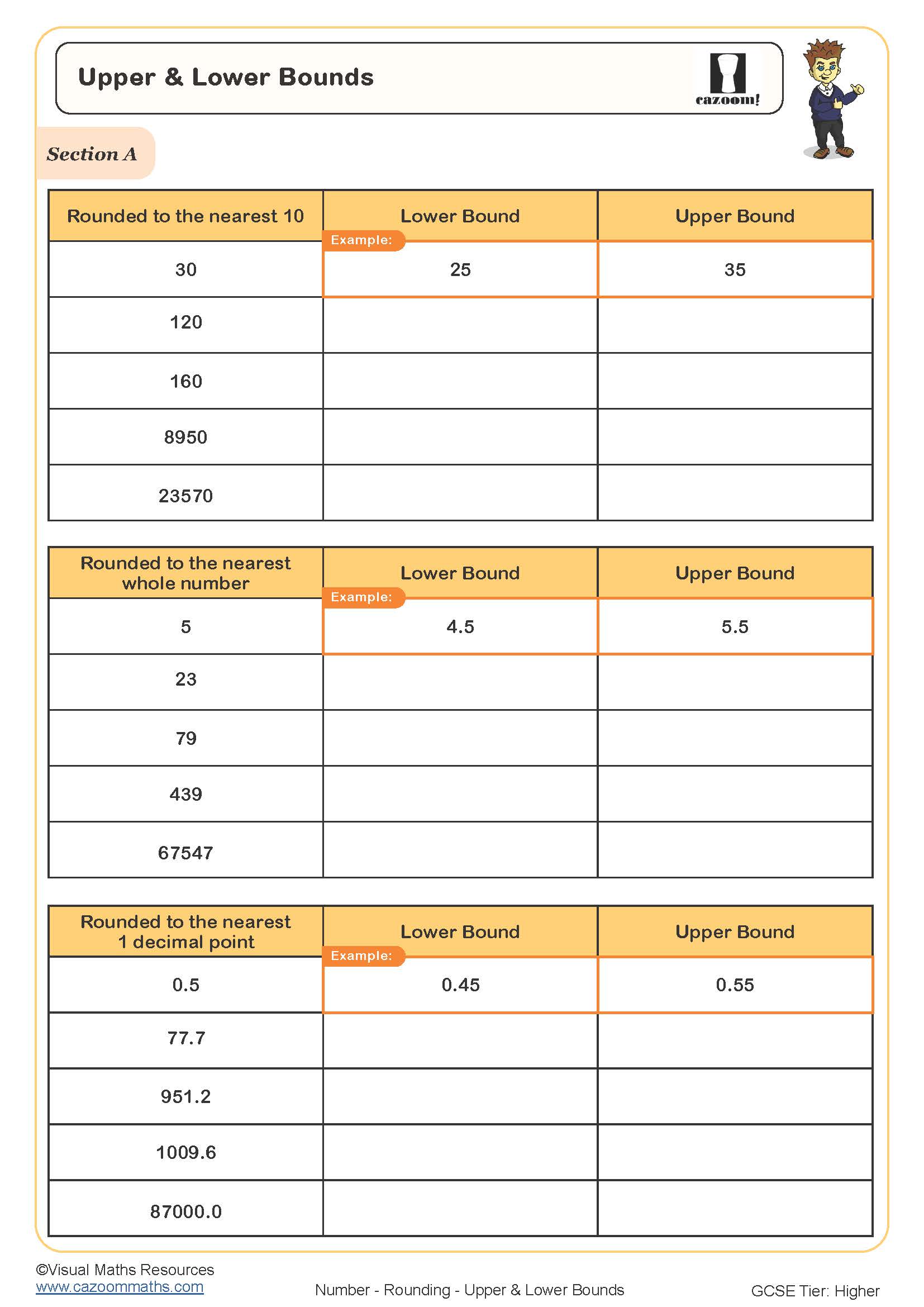
Upper and Lower Bounds
What should Year 8 students know about rounding?
A Year 8 rounding worksheet should cover rounding to any number of decimal places, rounding to significant figures, and applying these skills to measurement contexts and real-world problems. At KS3, students move beyond the whole number and one decimal place rounding from primary school to handle situations requiring precision across different magnitudes, from very large to very small numbers.
Teachers often notice that students apply the mechanical process correctly but struggle to decide how many decimal places or significant figures are appropriate for a given context. For instance, when calculating the area of a rectangle with measurements given to one decimal place, students might give an answer to five decimal places rather than recognising that two decimal places would be more appropriate. Exam mark schemes penalise answers that show unrealistic precision, so developing this contextual awareness is essential alongside the technical skill.
Which year groups study rounding?
These worksheets are designed specifically for Year 8 students working within the KS3 National Curriculum. At this stage, rounding becomes more sophisticated than the introductory work from Key Stage 2, with students expected to handle significant figures confidently and apply rounding appropriately in problem-solving contexts, including those involving standard form and estimation.
The progression from KS2 to Year 8 involves moving from rounding whole numbers and simple decimals to making decisions about appropriate degrees of accuracy. Year 8 students should be comfortable rounding to any number of decimal places, understand why 2.65 rounds to 2.7 (not 2.6) when using the standard convention, and recognise that the first significant figure in 0.00482 is the 4, not the zero. This depth of understanding supports their work in science practicals, where significant figures indicate measurement precision.
What's the difference between rounding to decimal places and significant figures?
Rounding to decimal places counts digits after the decimal point, whilst rounding to significant figures counts from the first non-zero digit regardless of where the decimal point sits. For example, 3.4827 rounded to two decimal places gives 3.48, but rounded to two significant figures gives 3.5. Students typically master decimal places first before tackling significant figures, where the counting position shifts depending on the number's magnitude.
This distinction matters considerably in scientific contexts. When a chemist measures 0.004762 grams of a substance, stating the result to three significant figures (0.00476 g) communicates the precision of the measurement equipment. Recording it as 0.005 g (one significant figure) implies far less precision. Scientists and engineers use significant figures to avoid false accuracy, ensuring calculations don't suggest greater precision than the original measurements warranted. Understanding this convention helps Year 8 students develop numeracy skills that transfer directly to their science investigations.
How can teachers use these rounding worksheets effectively?
The worksheets provide graduated practice from straightforward rounding exercises to problems requiring students to select appropriate degrees of accuracy. Many include worked examples that model the decision-making process, not just the mechanical steps, helping students understand when to apply each rounding method. The answer sheets allow students to self-assess, identifying patterns in their errors rather than simply marking answers correct or incorrect.
Teachers often use these worksheets for targeted intervention when assessment data shows students confusing decimal places with significant figures, or for homework following lessons on estimation and bounds. They work well for paired work where students compare their rounded answers and discuss any differences, particularly useful when questions ask students to justify their choice of accuracy. The structured progression makes them suitable for mixed-attainment teaching, with earlier questions accessible to students still consolidating basics whilst later problems challenge those ready for GCSE-style applications involving area, volume, and standard form.