Year 9 Calculator Methods Worksheets
What are calculator methods in Year 9 maths?
Calculator methods at Year 9 involve using scientific calculators effectively to solve problems involving powers, roots, standard form, trigonometric functions, and multi-step calculations. The National Curriculum for KS3 expects students to use calculators efficiently and interpret displays correctly, including understanding when answers appear in standard form or as decimal approximations.
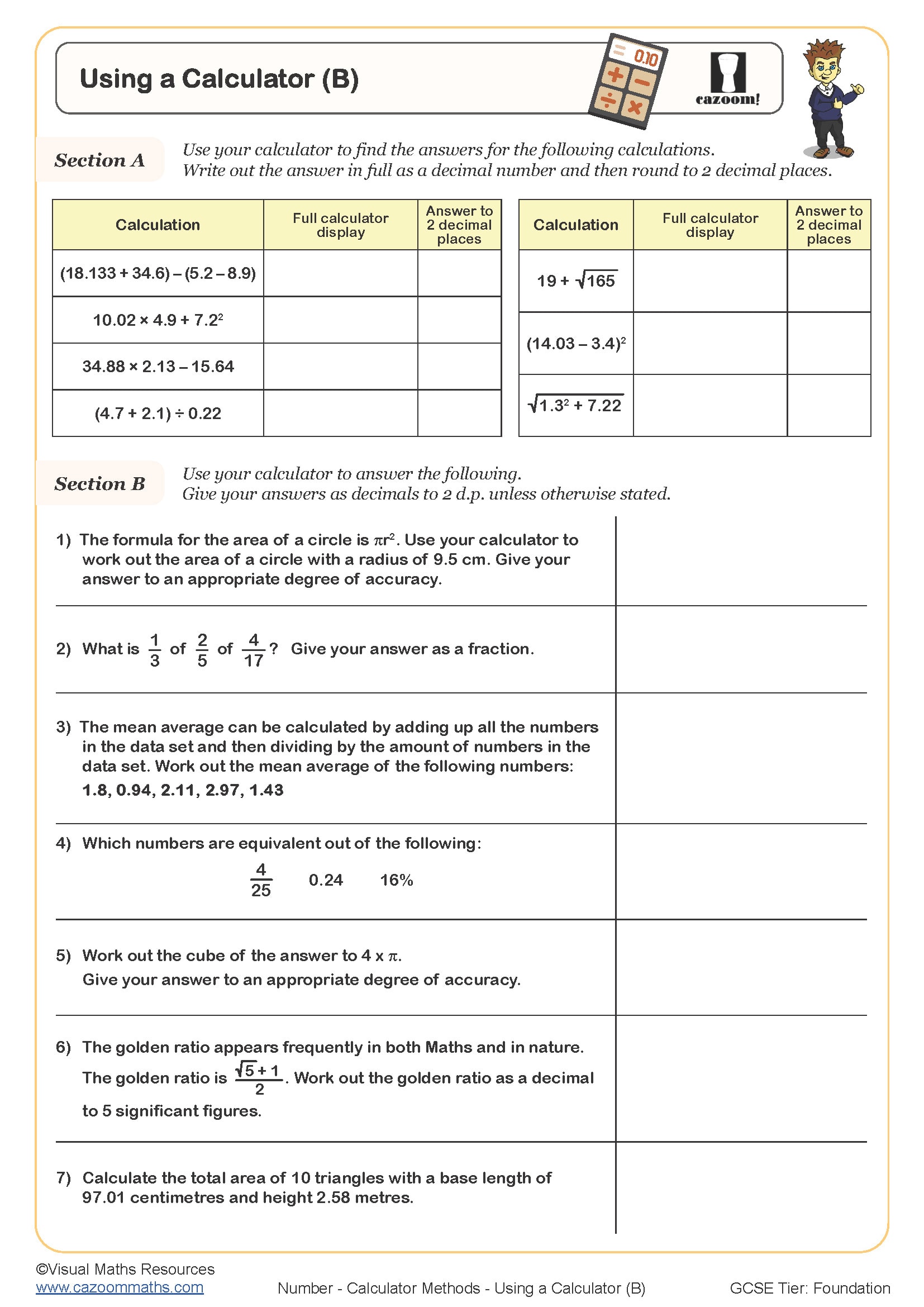
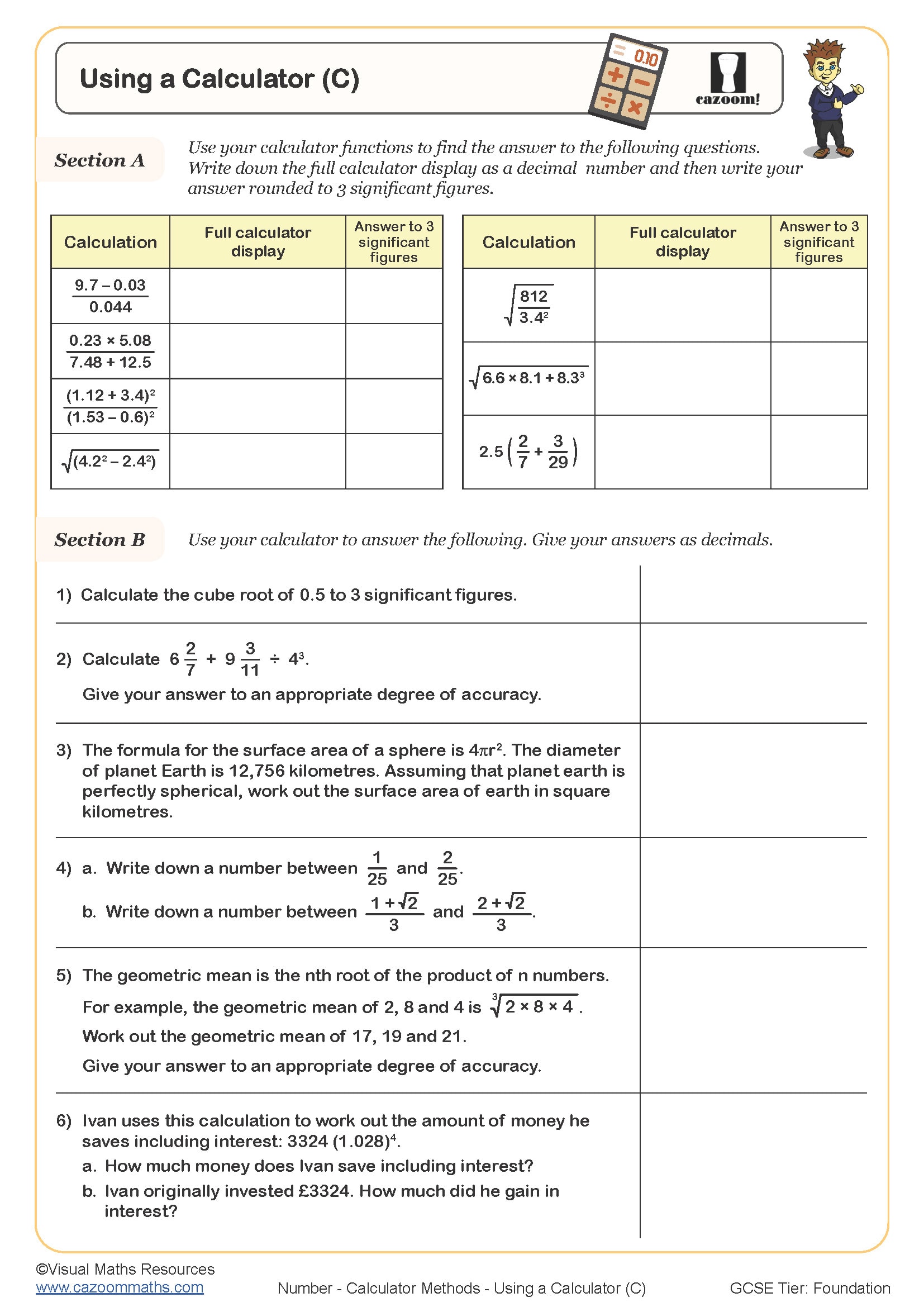
A common error occurs when students calculate something like 5 + 3 × 4 and enter it exactly as written without brackets, getting 32 instead of 17. Teachers often find that students need explicit teaching about when calculators follow BIDMAS automatically and when brackets must be inserted. Exam mark schemes at GCSE penalise incorrect calculator usage even when the method is sound, making these skills essential for progression.
Which year groups study calculator methods?
These calculator methods worksheets are designed for Year 9 students working within the KS3 curriculum. At this stage, students build on basic calculator skills from Years 7 and 8, moving towards the sophisticated calculator use required for GCSE maths, where calculator papers account for significant marks across both foundation and higher tiers.
The progression focuses on increasing complexity and application. Students move from simple multi-step calculations to using function keys for powers, roots, and eventually trigonometric ratios. By Year 9, students should confidently use memory functions, handle standard form conversions, and interpret calculator displays that show recurring decimals or approximations, preparing them for the calculator paper demands they'll face in Year 10 and beyond.
How do you use standard form on a calculator?
Standard form (scientific notation) on calculators uses an EXP or ×10^x button to enter numbers like 3.4 × 10⁵ efficiently. Students enter the significant figure part (3.4), press the EXP button, then enter the power (5). Understanding this prevents the common mistake of entering 3.4 × 10 × 10 × 10 × 10 × 10, which creates rounding errors and wastes time in exams.
Standard form connects directly to real-world STEM applications, from astronomy (distances between planets measured in metres like 1.5 × 10¹¹) to microbiology (bacterial sizes around 2 × 10⁻⁶ metres). Scientists and engineers use calculators with standard form constantly when handling very large or very small measurements. Students who master calculator standard form find physics calculations involving speed of light, chemistry mole calculations, and data science with large datasets far more manageable.
How do these calculator methods worksheets support learning?
The worksheets provide structured practice that builds from basic calculator operations to complex problem-solving scenarios. Questions progress systematically, allowing students to develop confidence with function keys, bracket usage, and display interpretation. Answer sheets enable immediate self-checking, helping students identify where errors occur—whether in entering the calculation or understanding the mathematical concept behind it.
Teachers use these resources effectively for targeted intervention with students who lack calculator confidence, as homework to reinforce classroom teaching, or as revision materials before assessments. They work well for paired activities where students compare calculator methods and check each other's display interpretations. The worksheets are particularly valuable for students moving from foundation to higher tier, where efficient calculator use becomes a significant advantage in completing papers within time limits.