Year 9 Trigonometry Worksheets
3D Trigonometry - Cuboids
3D Trigonometry and Pythagoras (A)
3D Trigonometry and Pythagoras (B)
Area of Triangles
Area of Triangles (With Clues)
Choosing the Correct Trig Rule
Describing Transformations of Trig Graphs
Finding Exact Trig Values
Labelling Right Angled Triangles
Pythagoras or Trigonometry? (A)
Pythagoras or Trigonometry? (B)
Sine Rule Cosine Rule and Area Mixed Exercise
Solving Trigonometric Equations
The Cosine Rule
The Cosine Rule - Finding Angles
The Cosine Rule - Finding Lengths
The Sine Rule
The Sine Rule - Finding Angles
The Sine Rule - Finding Lengths
The Tangent Ratio
Transformations of Trig Graphs (A)
Transformations of Trig Graphs (B)
Trigonometric Graphs (A)
Trigonometric Graphs (B)
Trigonometry (A) Missing Lengths
Trigonometry (B) - Missing Angles
Trigonometry (C) Missing Angles and Lengths
Trigonometry (D) Word Problems
Trigonometry Multi Step Problems
Using Exact Trig Values
Improve Test Results Using Our Ready-to-Print KS3 Geometry Activities Weekly
Mastering trigonometric ratios marks a pivotal moment in secondary mathematics, bridging geometric knowledge with algebraic thinking for powerful problem-solving capabilities. The transition from Year 8 geometry introduces students to precise angle-side relationships that unlock engineering, physics and advanced mathematical concepts . The practice of these core principles leads to the development of mathematical maturity, which is necessary for studying vectors, complex numbers, and calculus. The teacher observations demonstrate that students who study trigonometry from start to finish in a year develop better geometric visualisation skills. The methodical process of ratio calculation helps students build logical thinking abilities, which they can apply to various mathematical subjects.
Specific learning benefits include:
• Master the SOHCAHTOA memory technique effectively
• Develops calculator proficiency with trigonometric functions
• Strengthens right-angle triangle recognition skills
• Builds a foundation for GCSE higher content
• Connects abstract ratios to practical measurements
• Improves problem-solving strategy selection
• Enhances mathematical communication precision
Worksheet Topics at a Glance: Missing Lengths, Missing Angles, Tangent Ratio, and More
The design of progressive worksheets leads students from concrete triangle measurement to pictorial representation and abstract ratio calculation, which enables them to build both conceptual understanding and procedural fluency. The resources present worked solutions which show mathematical reasoning through step-by-step, systematic explanations. The lesson sequence builds up sine, cosine and tangent concepts step by step to avoid overwhelming students while keeping the right level of difficulty from start to finish.
The worksheets in this collection include:
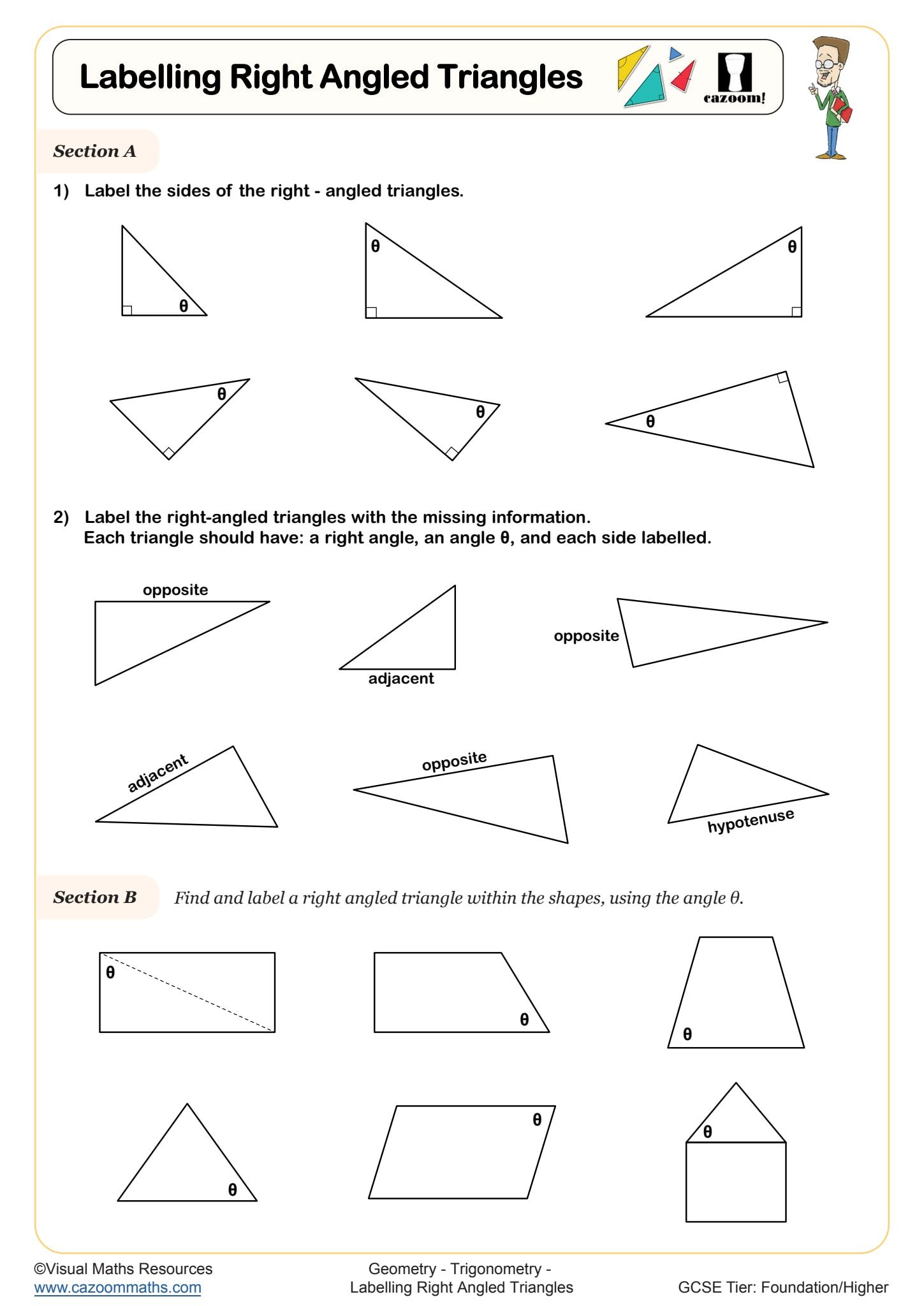
• Introduction to Trigonometric Ratios — establishing sine, cosine and tangent relationships through exploration
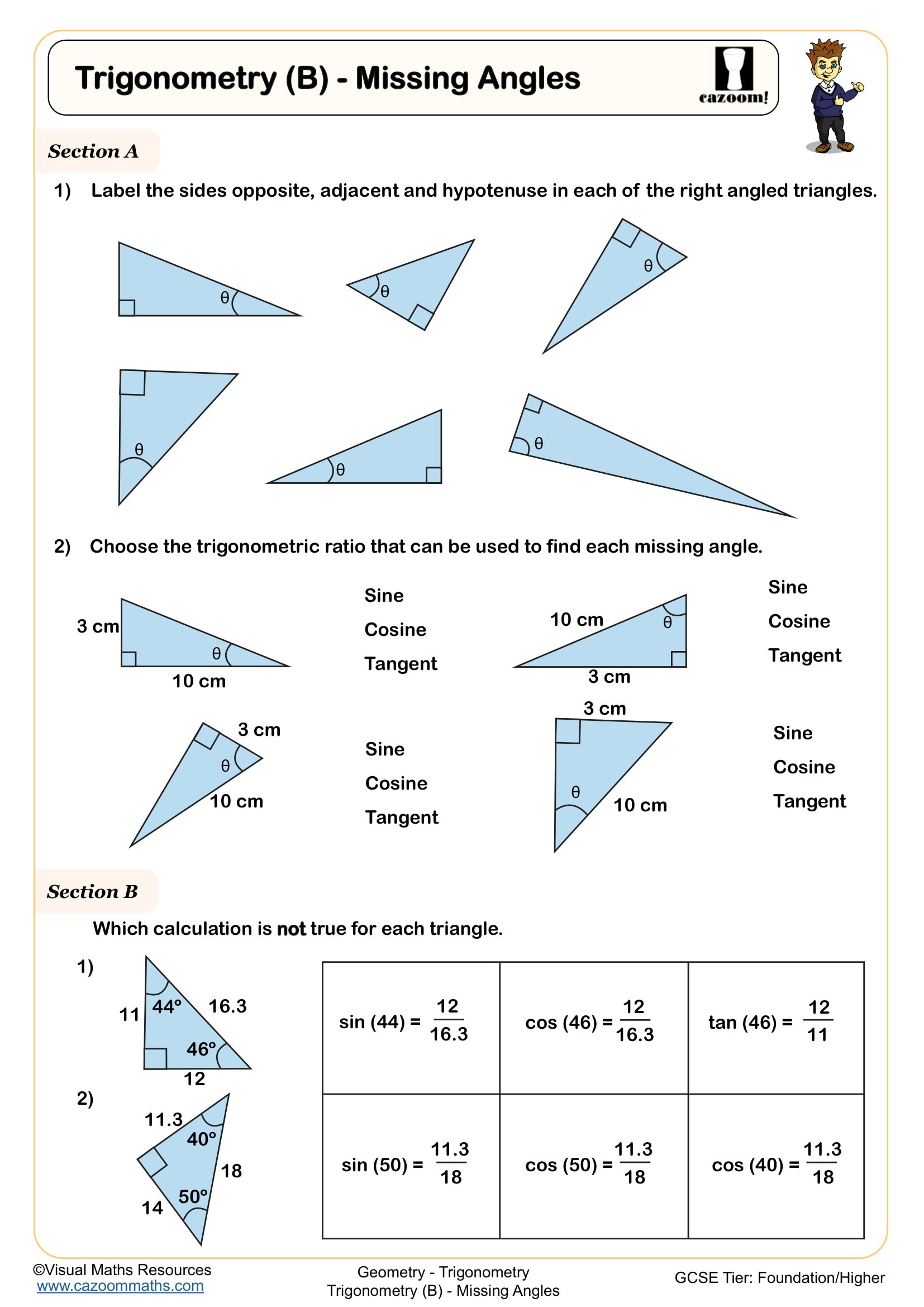
• SOHCAHTOA Practice — memorising ratio definitions using the famous mnemonic device
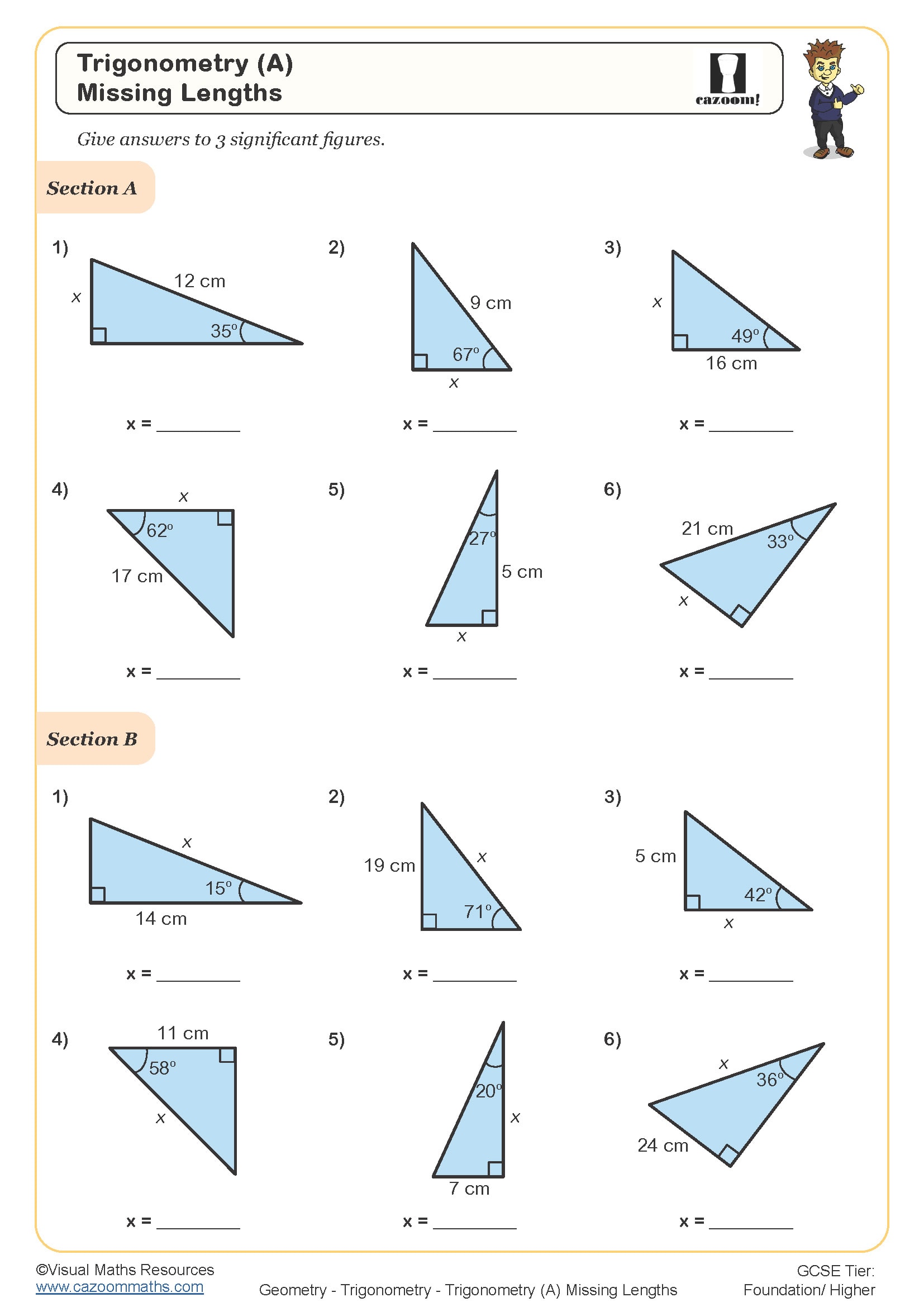
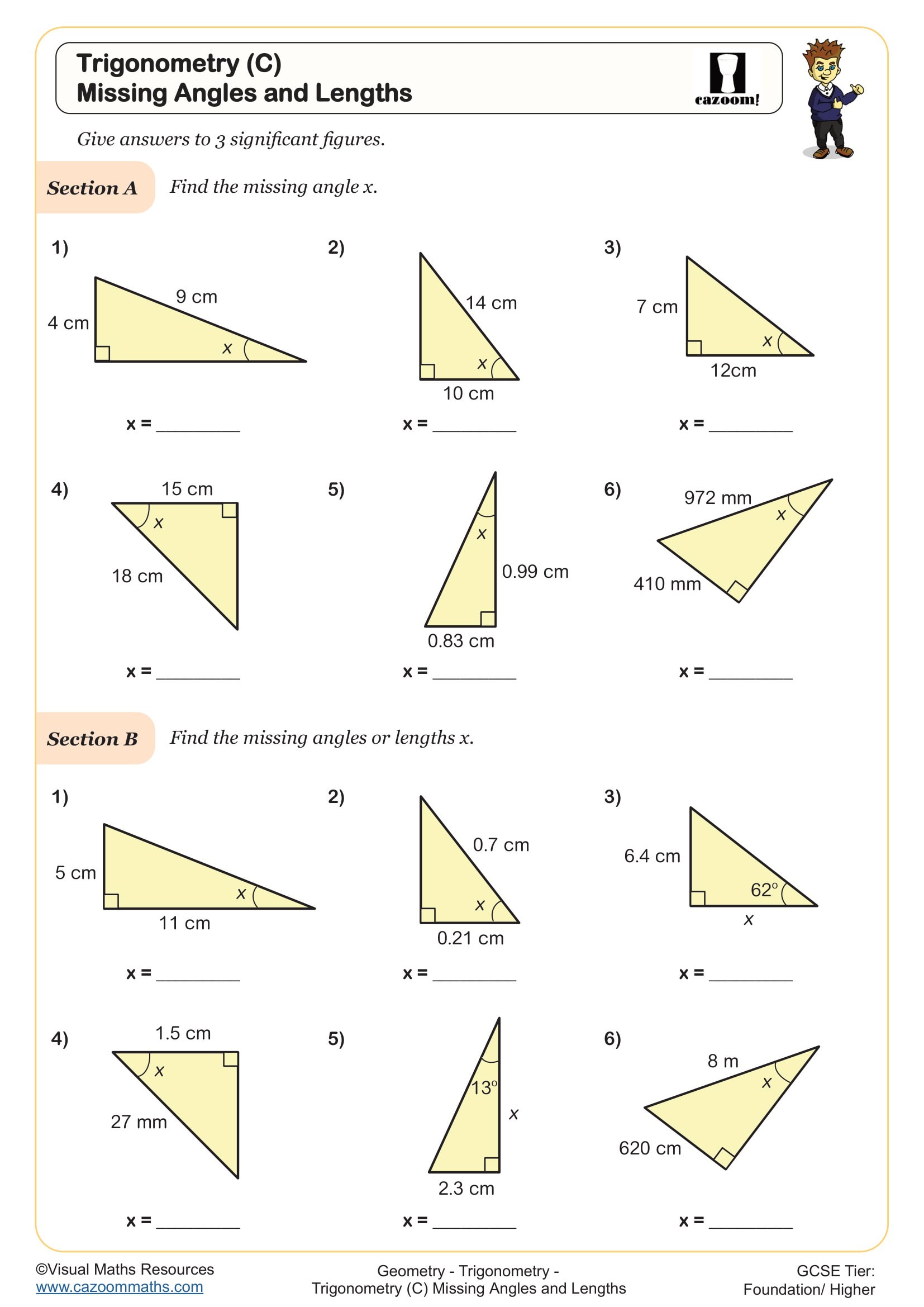
• Finding Missing Sides — calculating unknown lengths using given angles and measurements
• Finding Missing Angles — determining angle sizes from known side lengths
• Mixed Trigonometry Problems — combining multiple techniques within a single question
• Angles of Elevation and Depression — solving vertical distance problems using horizontal observations
• Bearings and Navigation — applying trigonometry to directional movement calculations
• Real-World Applications — connecting classroom learning to practical measurement scenarios
Professional Benefits: Why Schools Choose Year 9 Trigonometry Resources for Easy Learning
Teachers who focus on math education select resources based on classroom features which enable personalised learning and decrease their preparation work. The combination of accessible content with challenging extension questions enables all students to advance from their current level while providing suitable difficulties for more advanced learners. The use of clear formatting helps decrease mental effort because it enables students to concentrate on mathematical problems instead of trying to understand the instructions. Teachers can save time during marking through answer sheets, which maintain the assessment standards needed for formal exams. The uniform structure between worksheets enables students to create learning patterns through routine, which maximises their study time and decreases their need for extra teaching assistance. The built-in differentiation features of tiered questions allow teachers to support students with different abilities through their existing materials without creating additional content.
Practical Trigonometry Applications Beyond School Mathematics
Understanding trigonometric principles opens countless career pathways and enhances everyday problem-solving capabilities far beyond classroom walls. For example-
• Architecture relies on angle calculations for structural stability and aesthetic design proportions.
• Sports science uses elevation angles to optimise throwing trajectories and equipment positioning.
• Navigation systems calculate distances and directions continuously using trigonometric principles.
• Construction workers determine roof pitches and staircase angles through ratio applications.
• Game developers program realistic physics using sine and cosine functions extensively.
• Surveyors measure inaccessible heights using angles of elevation from known distances.
• Solar panel installers calculate optimal tilt angles for maximum energy generation.
• Film cinematographers position cameras using trigonometric calculations for desired perspectives.