Inequalities on a Number Line RESOURCE (FREE DOWNLOAD)

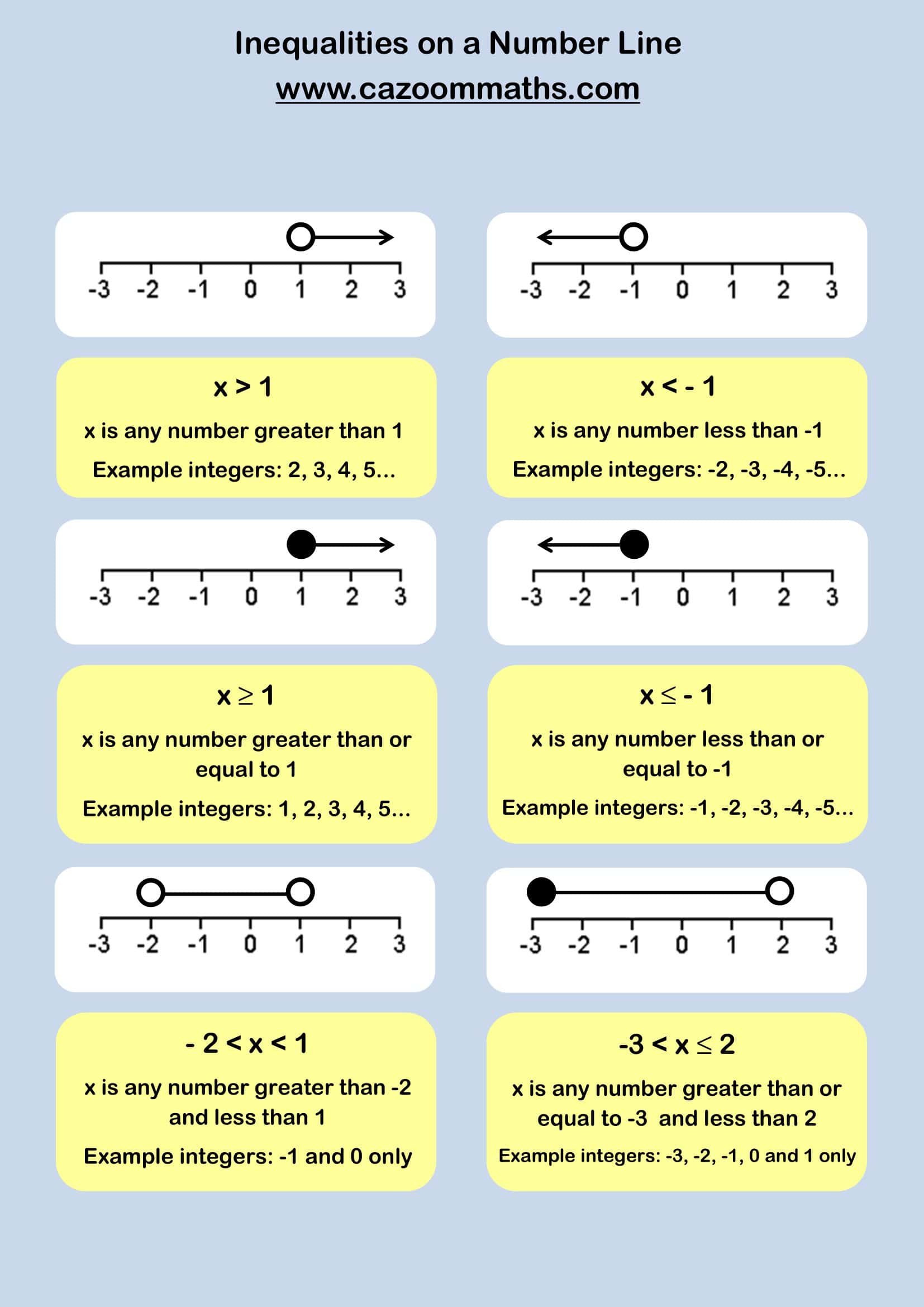
This resource gives examples of how to display inequalities on a number line and provides integer examples for each.

Inequalities on a Number Line: A Complete Guide

The basic concept of Inequalities is an important part of the Algebra curriculum. The knowledge of Inequalities will help your KS3 students compare numbers and show a range of possible values rather than a simple single solution. One of the best ways to understand and calculate inequalities is by plotting them on a number line. Our ‘Inequalities on a Number Line’ is a perfect teaching resource that will guide you to explain how to represent inequalities on a number line with clear and appropriate examples.

What is an Inequality?

The concept of inequality can be easily explained as a mathematical statement that compares two different values using symbols, such as-

• x > a → x is greater than a
• x < a → x is less than a
• x ≥ a → x is greater than or equal to a
• x ≤ a → x is less than or equal to a
• a < x < b → x is between a and b, but not equal to them
• a ≤ x ≤ b → x is between a and b, including both values

How to Represent Inequalities on a Number Line

On the other hand, a number line provides a clear visual representation of any inequality solutions.

Key Notations:

Here are the key notations that we need to keep in mind-

• Open Circle (○) → The value is NOT included (strict inequality < or >).
• Closed Circle (●) → The value IS included (inequality ≤ or ≥).

Inequality Number Line Examples

Now, let’s take some examples-

Example 1: x>1x > 1x>1

• Represents all values greater than 1.
• Open circle at 1, with an arrow moving right.

Example integers: 2, 3, 4, 5, …

Example 2: x≤−1x \leq -1x≤−1

• Represents all values less than or equal to -1.
• Closed circle at -1, with an arrow moving left.

Example integers: -1, -2, -3, -4, …

Example 3: −2<x<1-2 < x < 1−2<x<1

• Represents all values between -2 and 1.
• Open circles at -2 and 1, no arrows.

Example integers: -1, 0 only (since -2 and 1 are NOT included).

Example 4: −3≤x<2-3 \leq x < 2−3≤x<2

• Represents values between -3 and 2, including -3 but not 2.
• Closed circle at -3, open circle at 2.

Example integers: -3, -2, -1, 0, 1 only.

Why Use a Number Line for Inequalities?

1. Using a number line makes it a lot more easier to understand and calculate inequality solutions.
2. A Number Line helps us to visualize how one number relates to other numbers.
3. This idea for solving algebra problems involving inequalities.