Year 11 Indices Worksheets
Master Index Laws with Step-by-Step GCSE Indices Worksheets
Finding quality indices worksheet PDF resources that actually help students understand (rather than just practice) can be frustrating. We've created these worksheets differently - each one includes detailed worked solutions that show the complete thinking process behind index law questions. Students get plenty of practice with indices math questions while building genuine understanding. It's actually quite satisfying when you see that lightbulb moment happen!
Essential Index Laws and Skills Covered in These Worksheets
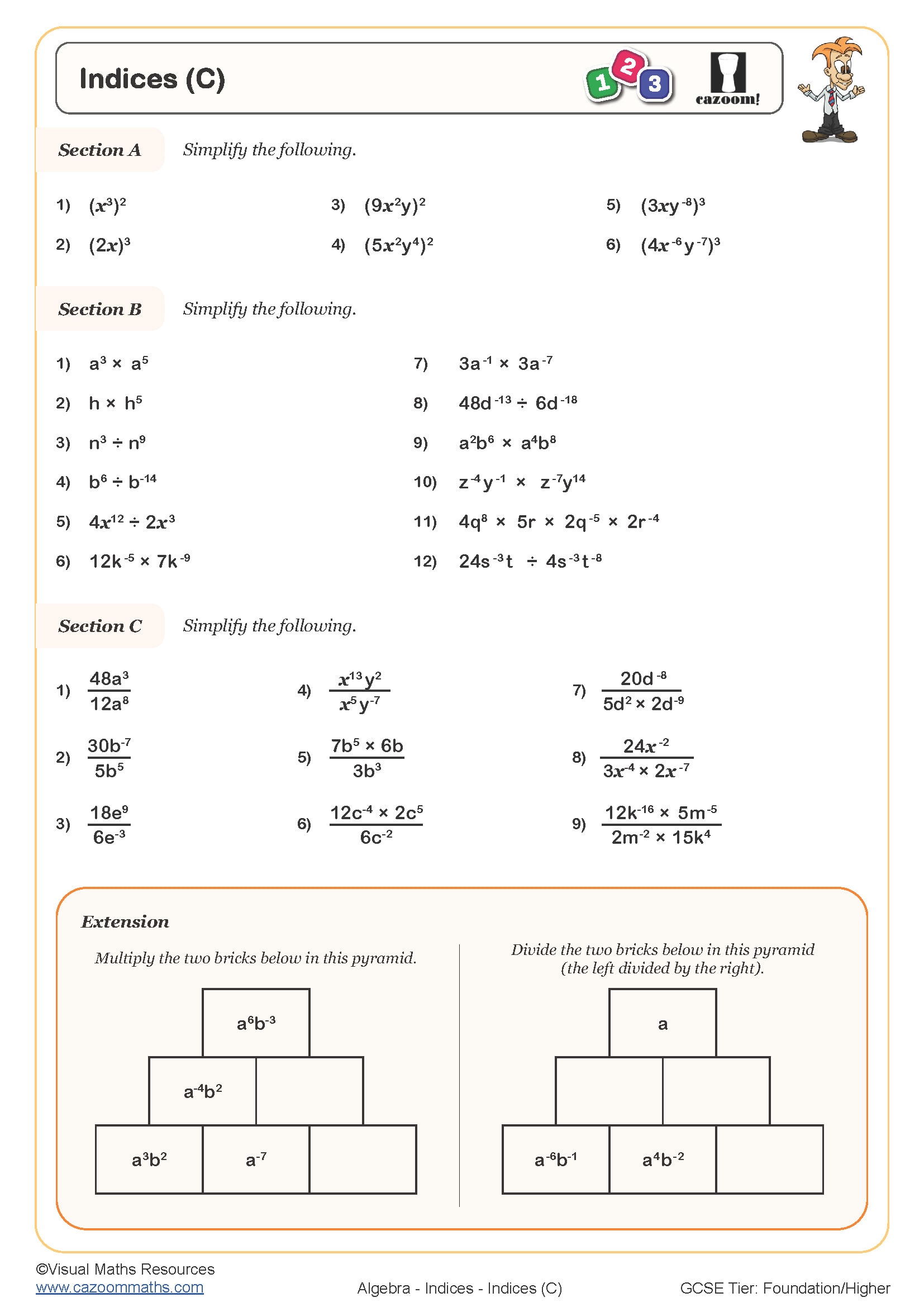
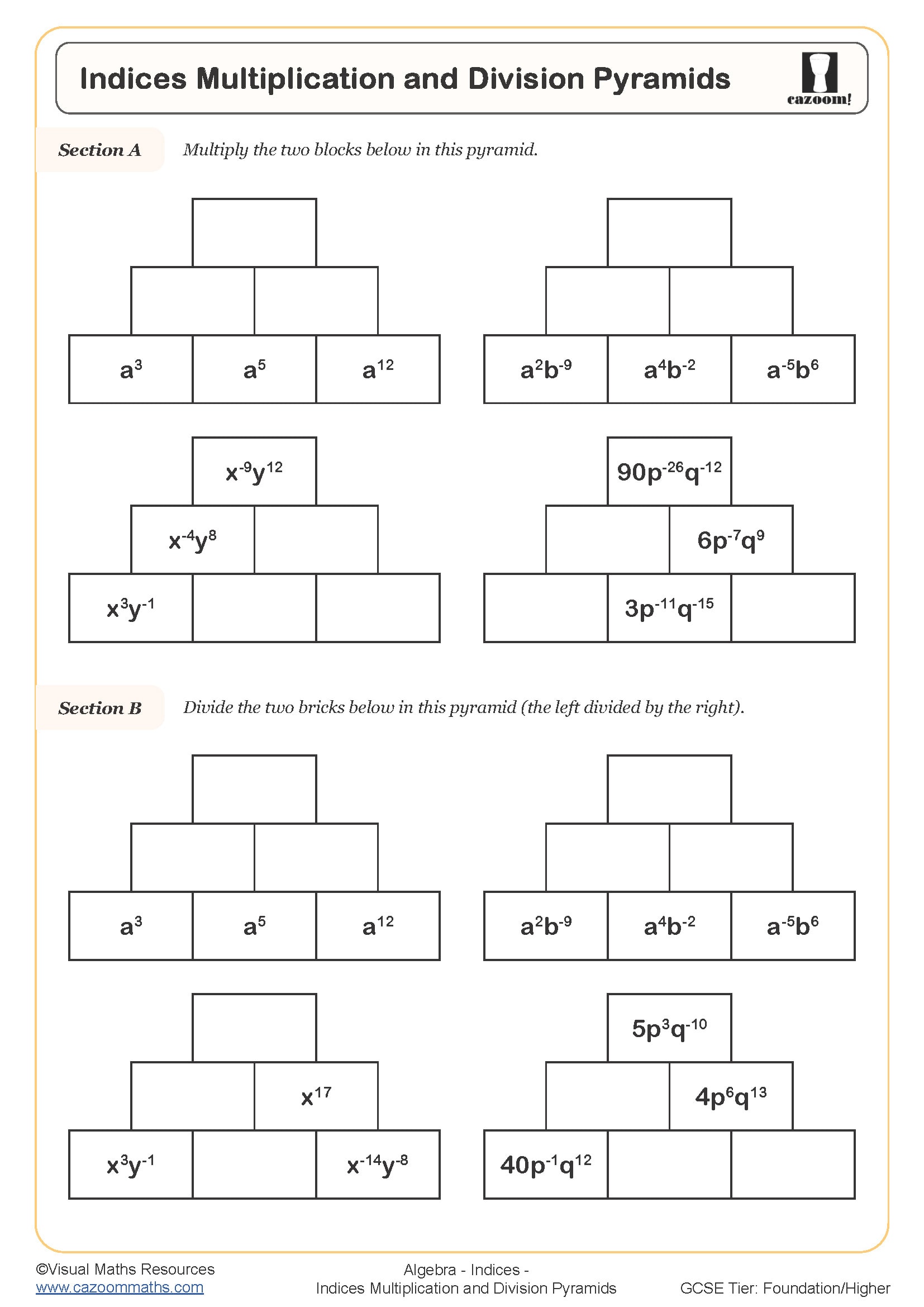
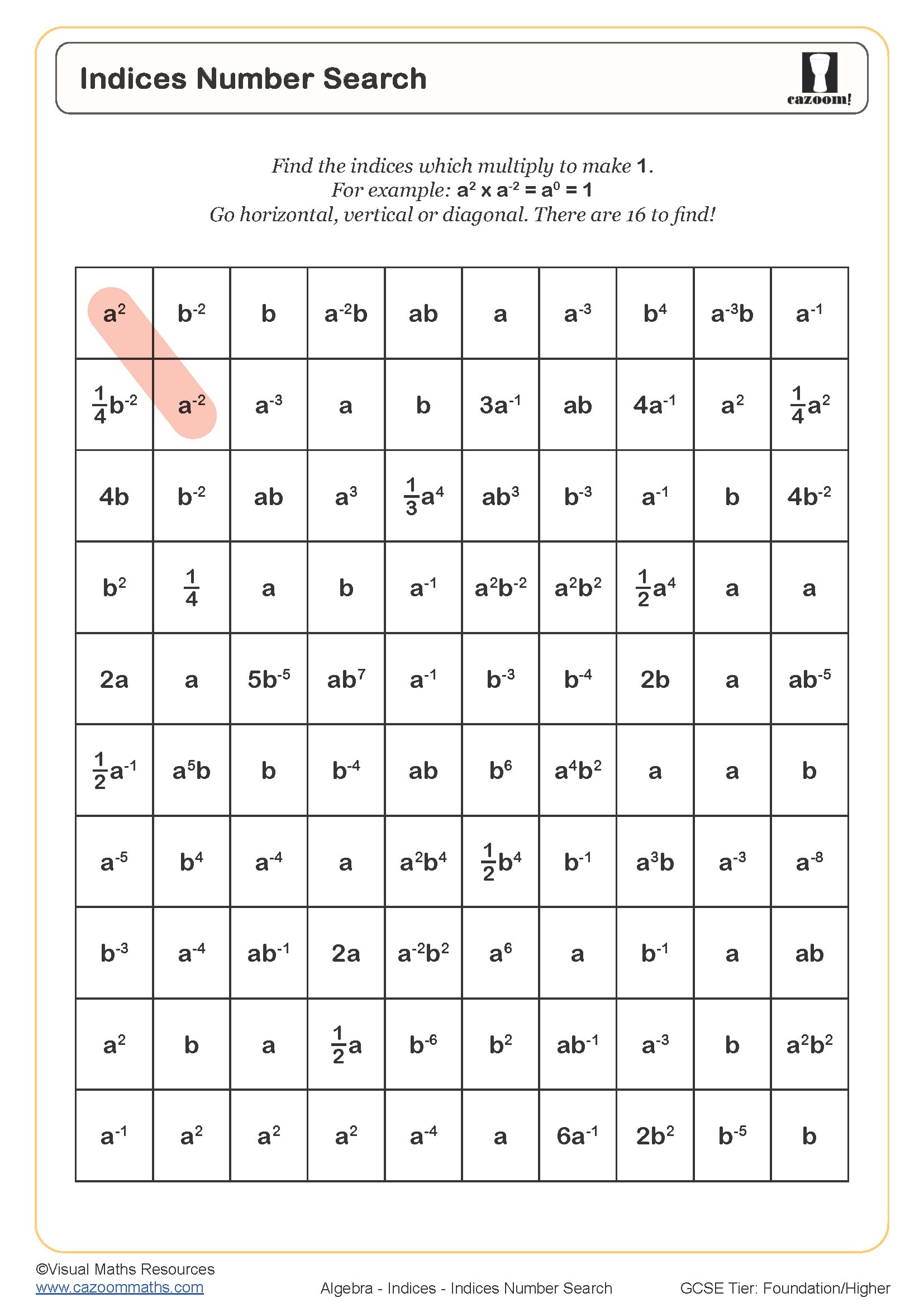
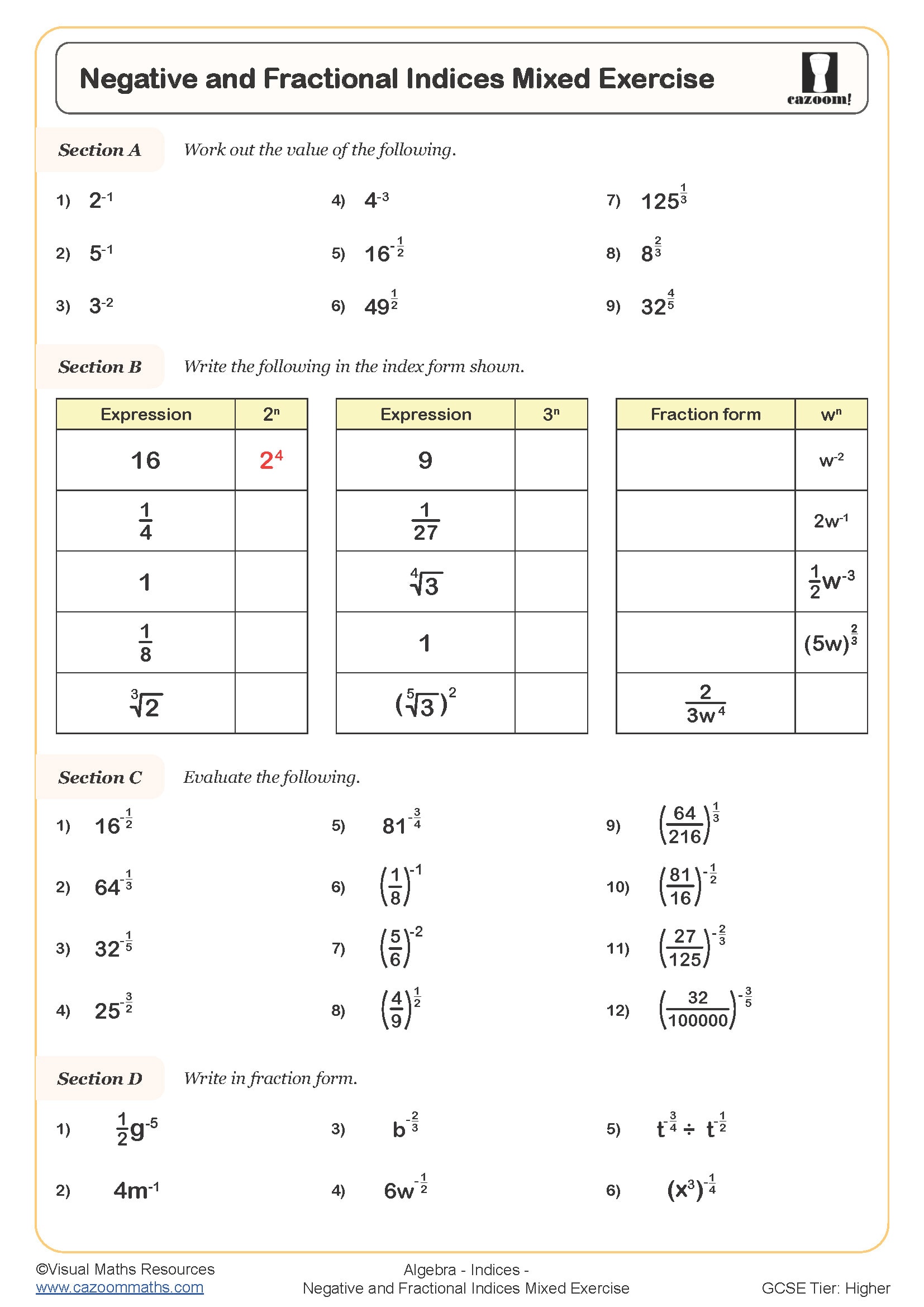
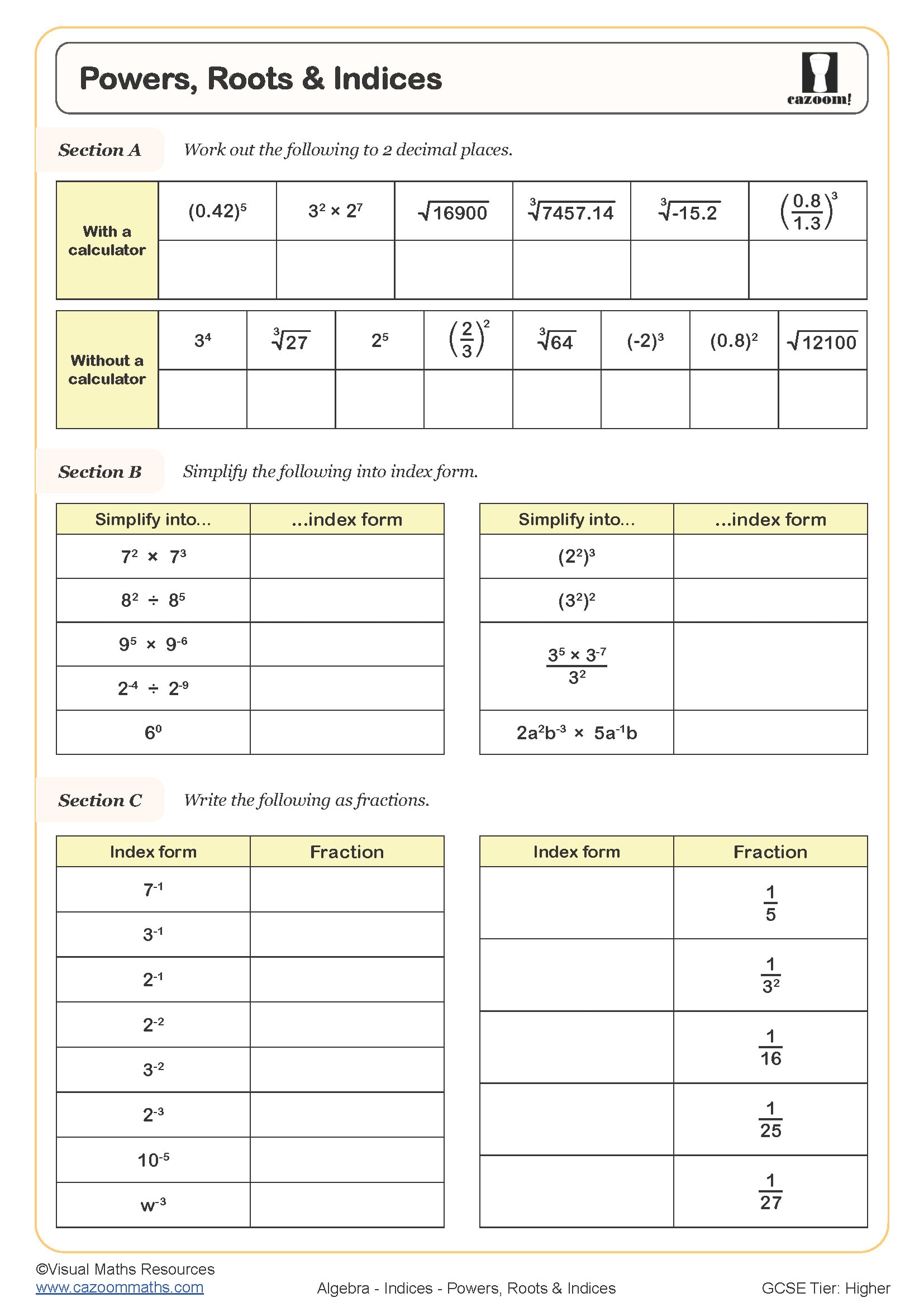
We've packed quite a lot into these indices worksheets! The progression starts with basic index notation worksheet concepts and builds up to complex algebraic manipulation. Students particularly love the visual approach we use for explaining why index laws work the way they do. Each worksheet covers multiplication and division rules, powers of powers, negative and fractional indices, plus those tricky zero index problems that always catch students out.
Why Year 11 Students Need Targeted Index Laws Practice
Here's what we've noticed after years of teaching indices: students who get regular, structured practice consistently outperform those who don't. The connection between understanding index laws and GCSE success is undeniable, especially in algebraic manipulation questions. These worksheets provide the focused practice that transforms hesitant students into confident problem-solvers.
• Builds fluency with index notation and mathematical reasoning
• Strengthens exam technique for GCSE questions
• Develops pattern recognition for complex index problems
• Improves speed and accuracy under timed conditions
• Creates solid foundations for A-Level mathematics
Real-World Applications Where Students Actually Use Index Laws
Students always ask, "When will I ever use this?" - and indices are surprisingly everywhere! These skills connect directly to physics (calculating exponential decay), geography (population growth models), and business studies (compound interest calculations). We also see indices in computer science algorithms and engineering calculations. It's genuinely rewarding when students realise how these mathematical tools unlock understanding across multiple subjects.
• Scientific notation in chemistry and physics experiments
• Population modelling in geography and environmental studies
• Compound interest calculations in business and economics
• Computer algorithms and data processing speeds
• Engineering measurements and scale factor calculations
• Medical dosage calculations involving exponential functions