Year 11 Non-Linear Functions Worksheets
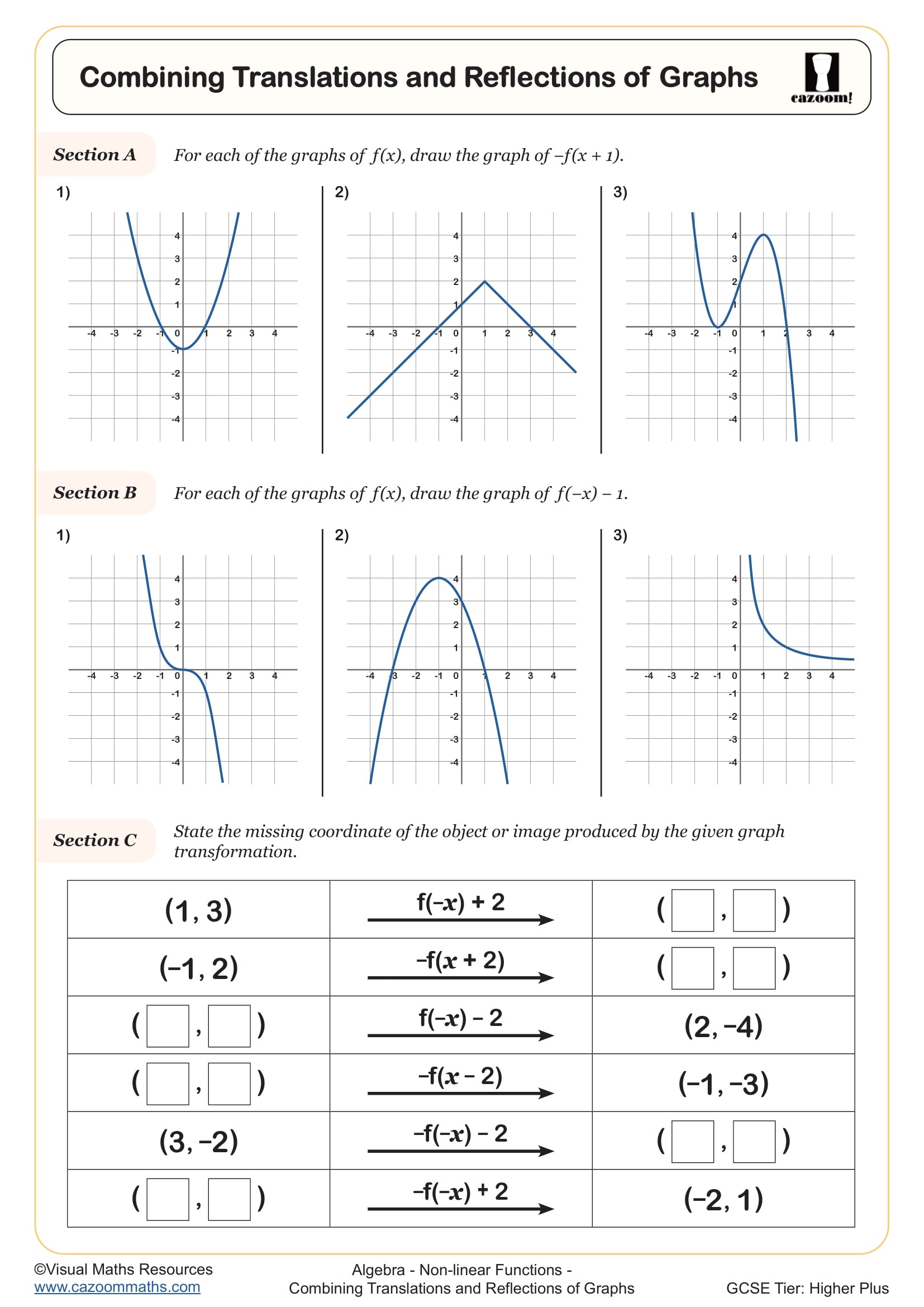
Combining Translations and Reflections of Graphs
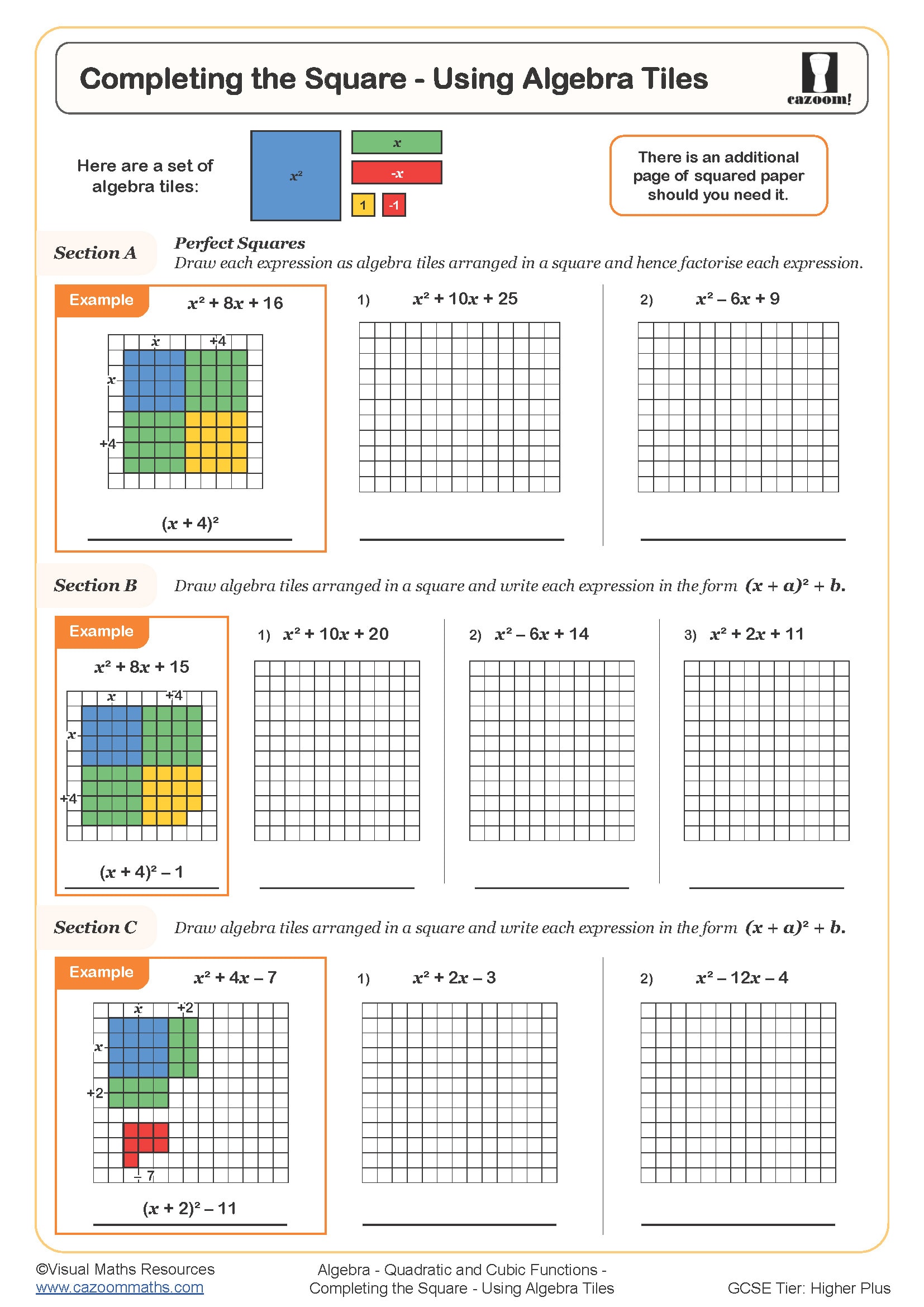
Completing the Square - Using Algebra Tiles
Completing the Square (A)
-Worksheet.jpg?w=3840)
Completing the Square (B)
/Cazoom-Maths-Non-Linear-Functions-Completing-the-Square-(B)-Worksheet.jpg?w=3840)
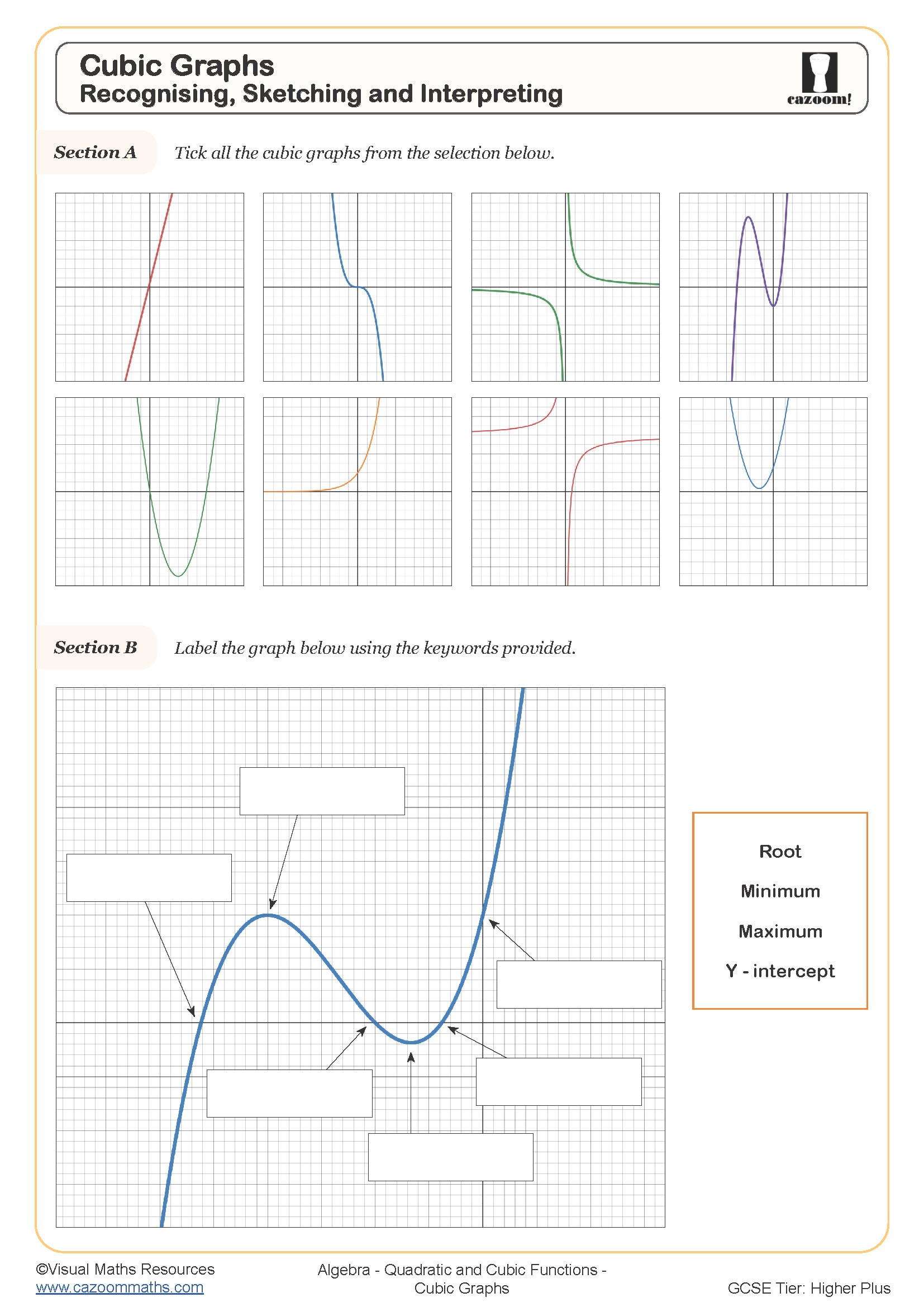
Cubic Graphs - Recognising, Sketching and Interpreting
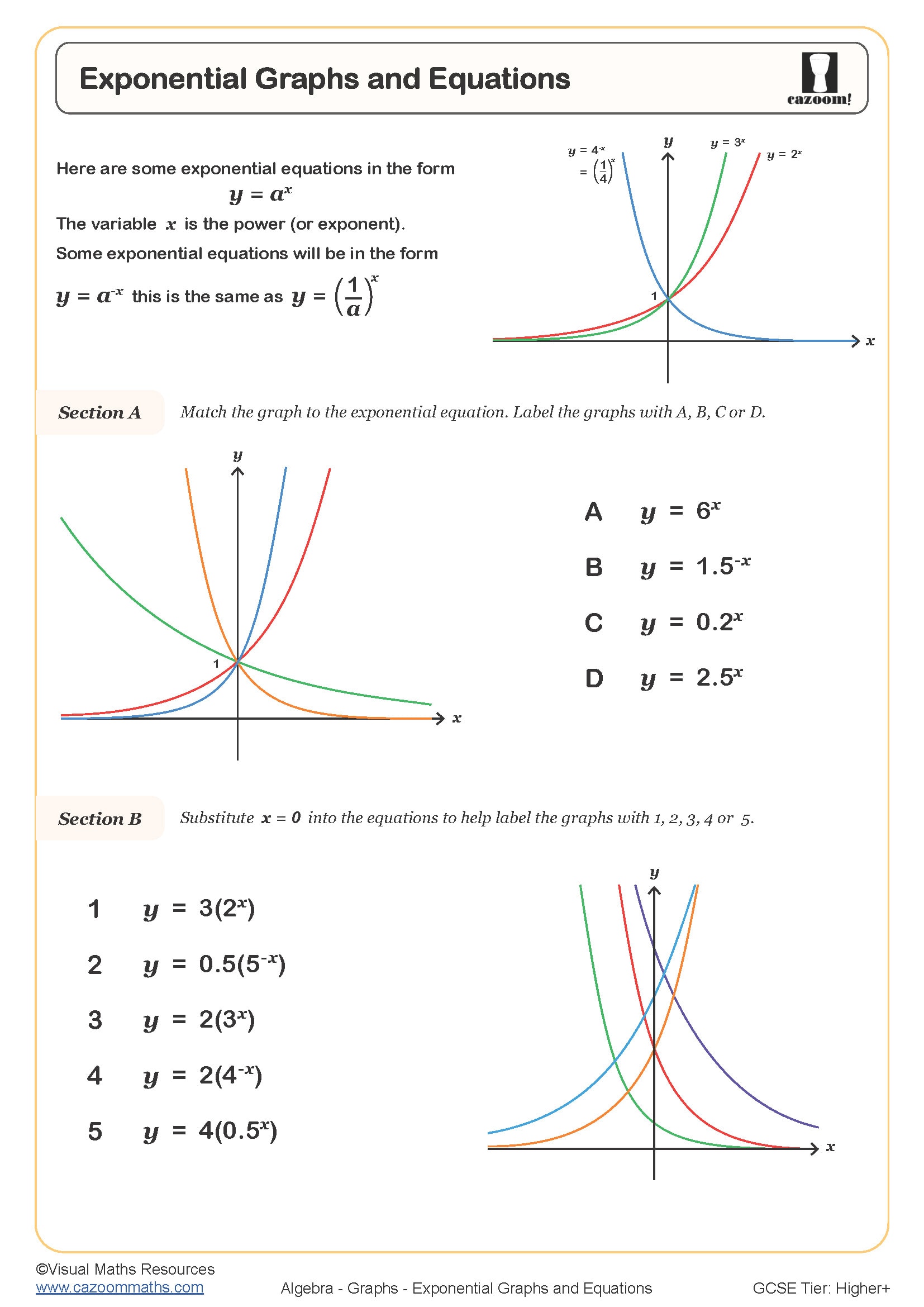
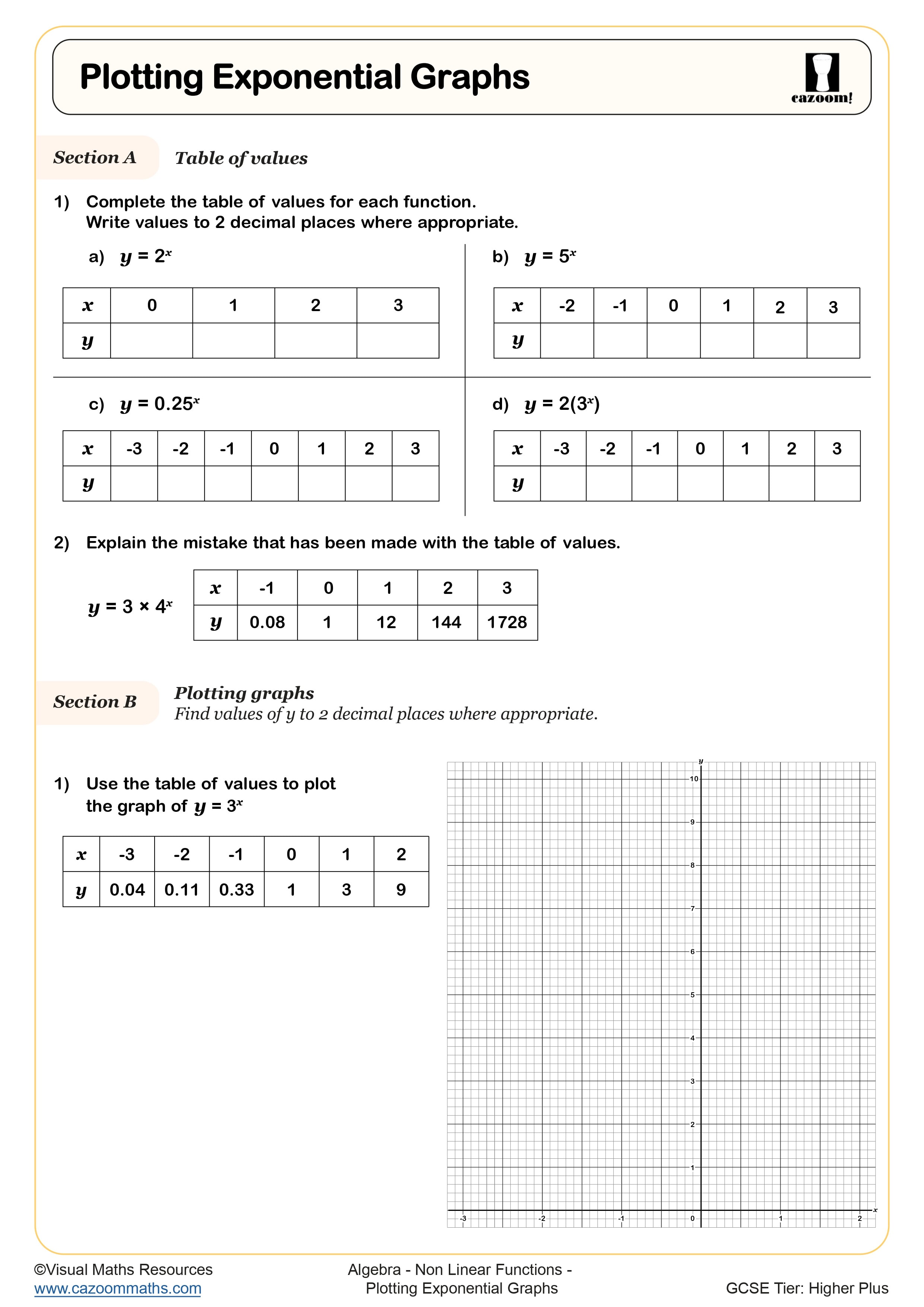
Exponential Graphs and Equations
Identify Linear and Non Linear Functions

Investigating Quadratic Graphs

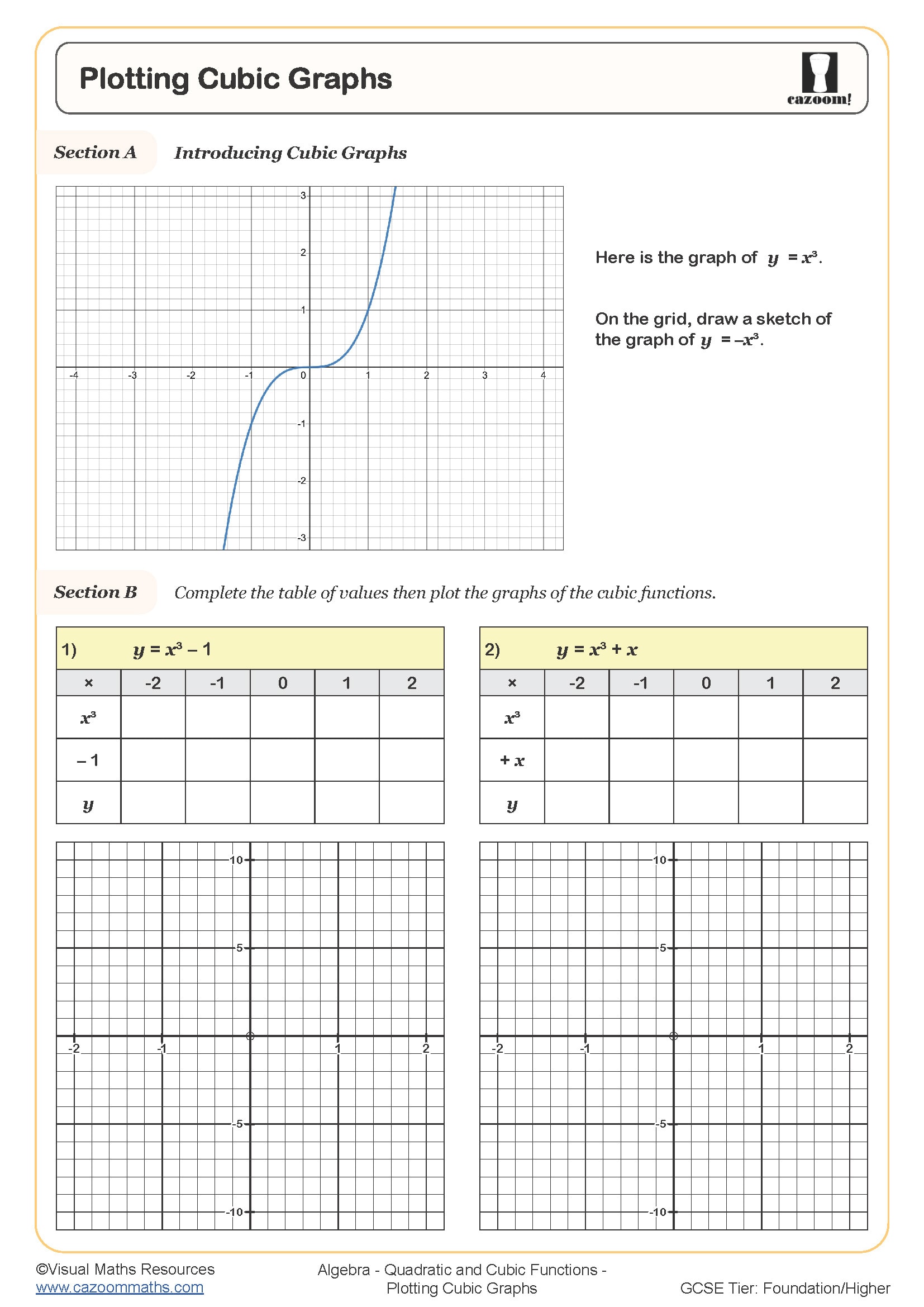
Plotting Cubic Graphs
Plotting Exponential Graphs
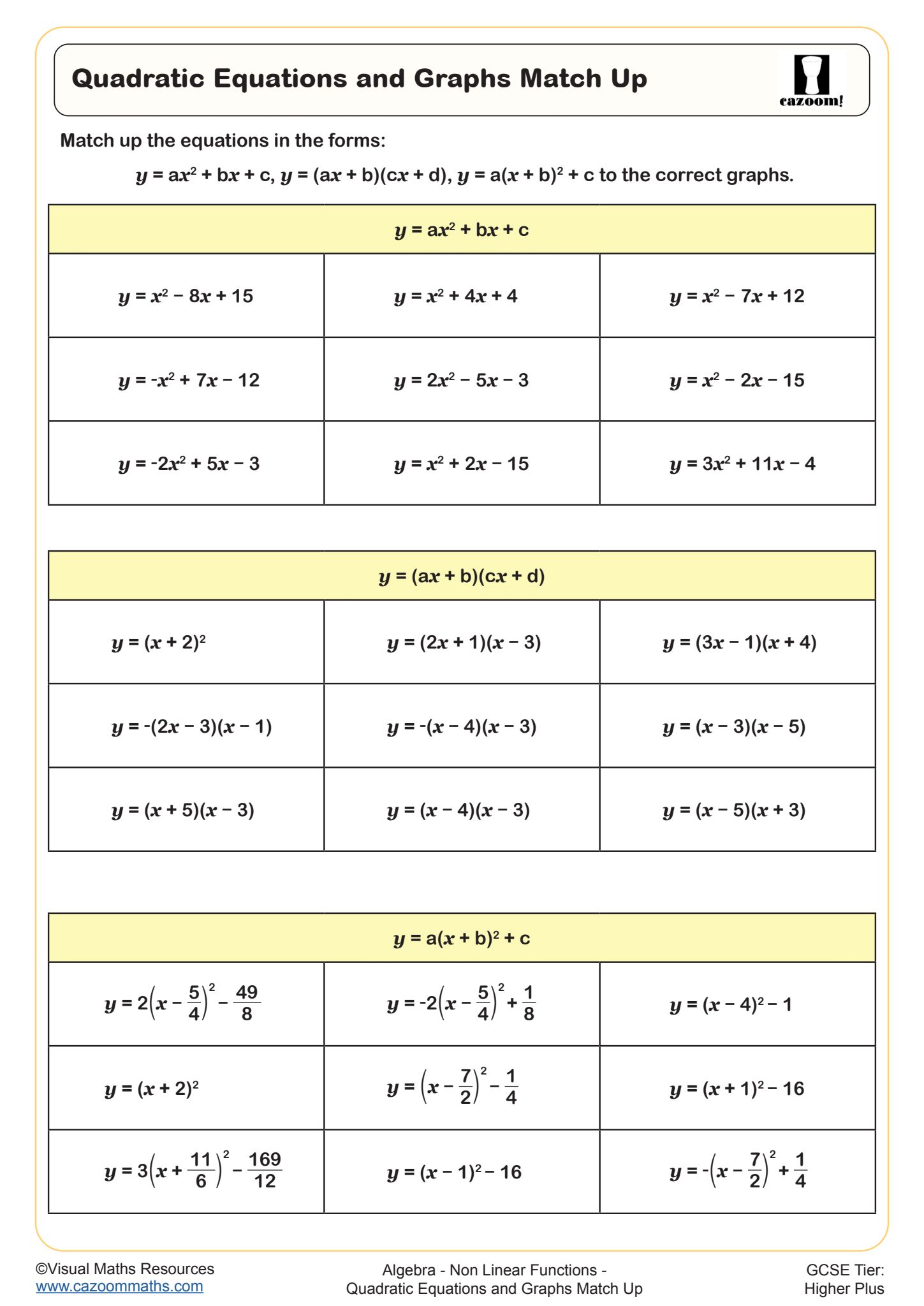
Quadratic Equations and Graphs Match Up
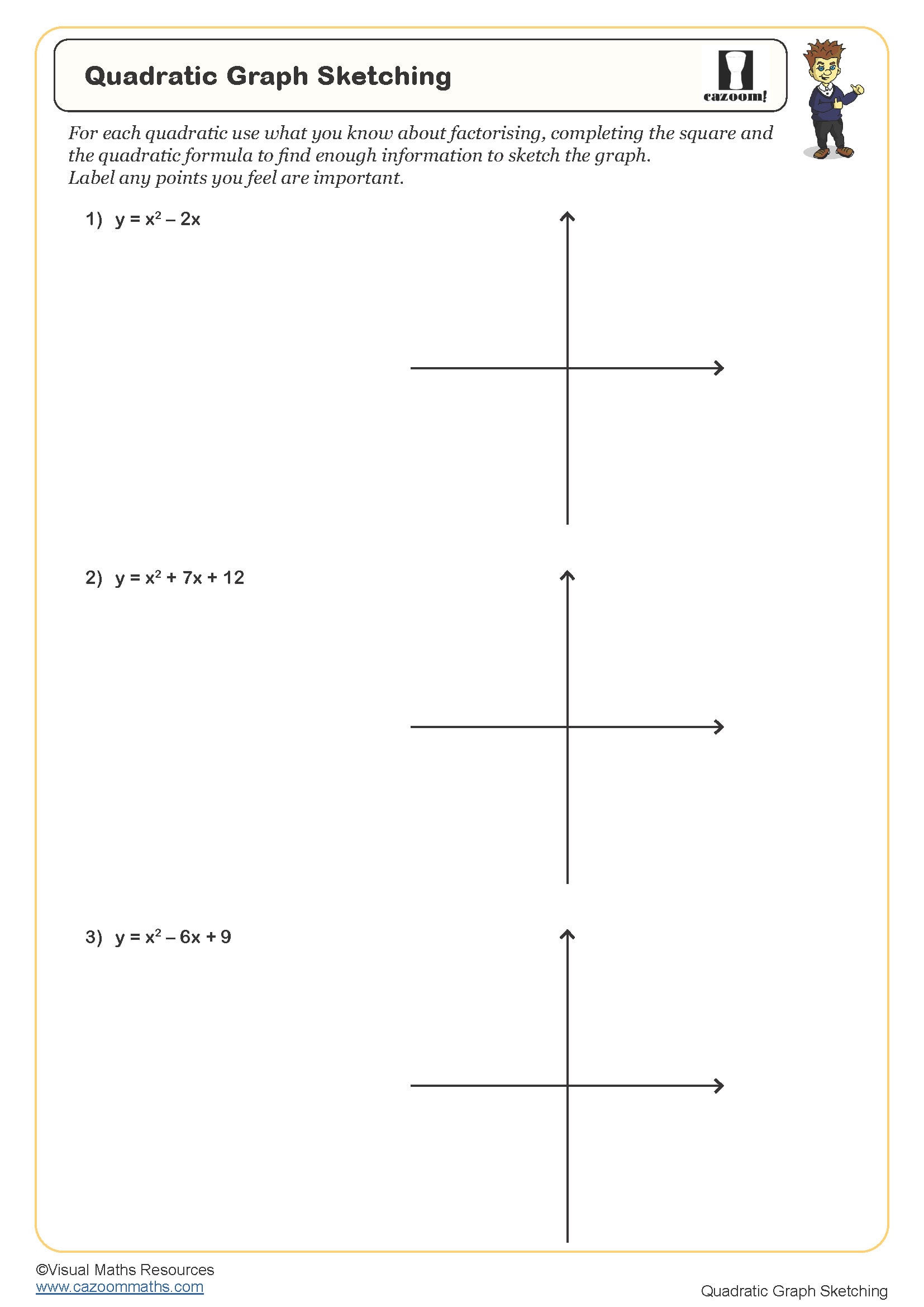
Quadratic Graph Sketching
Quadratic Graphs (A)
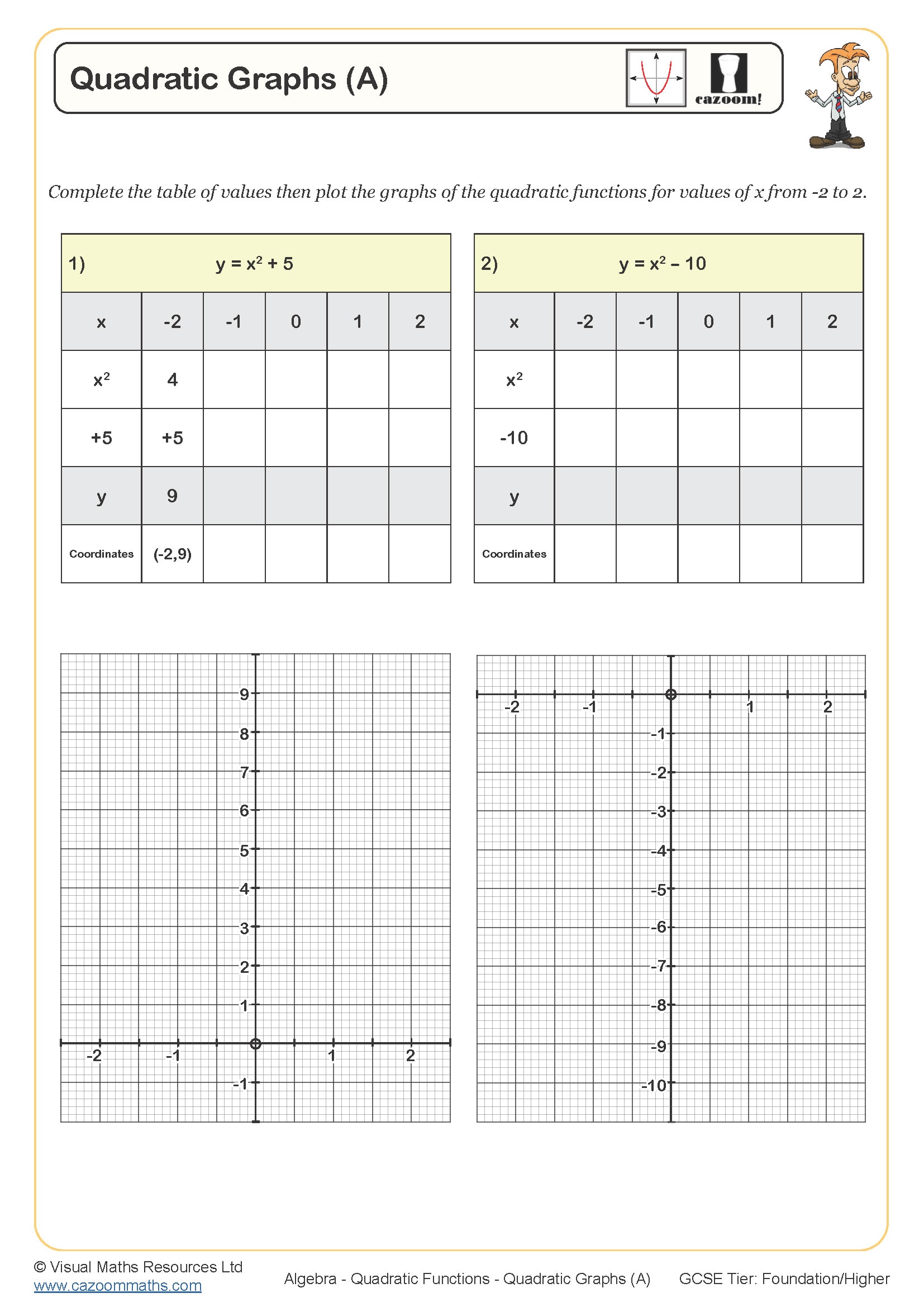
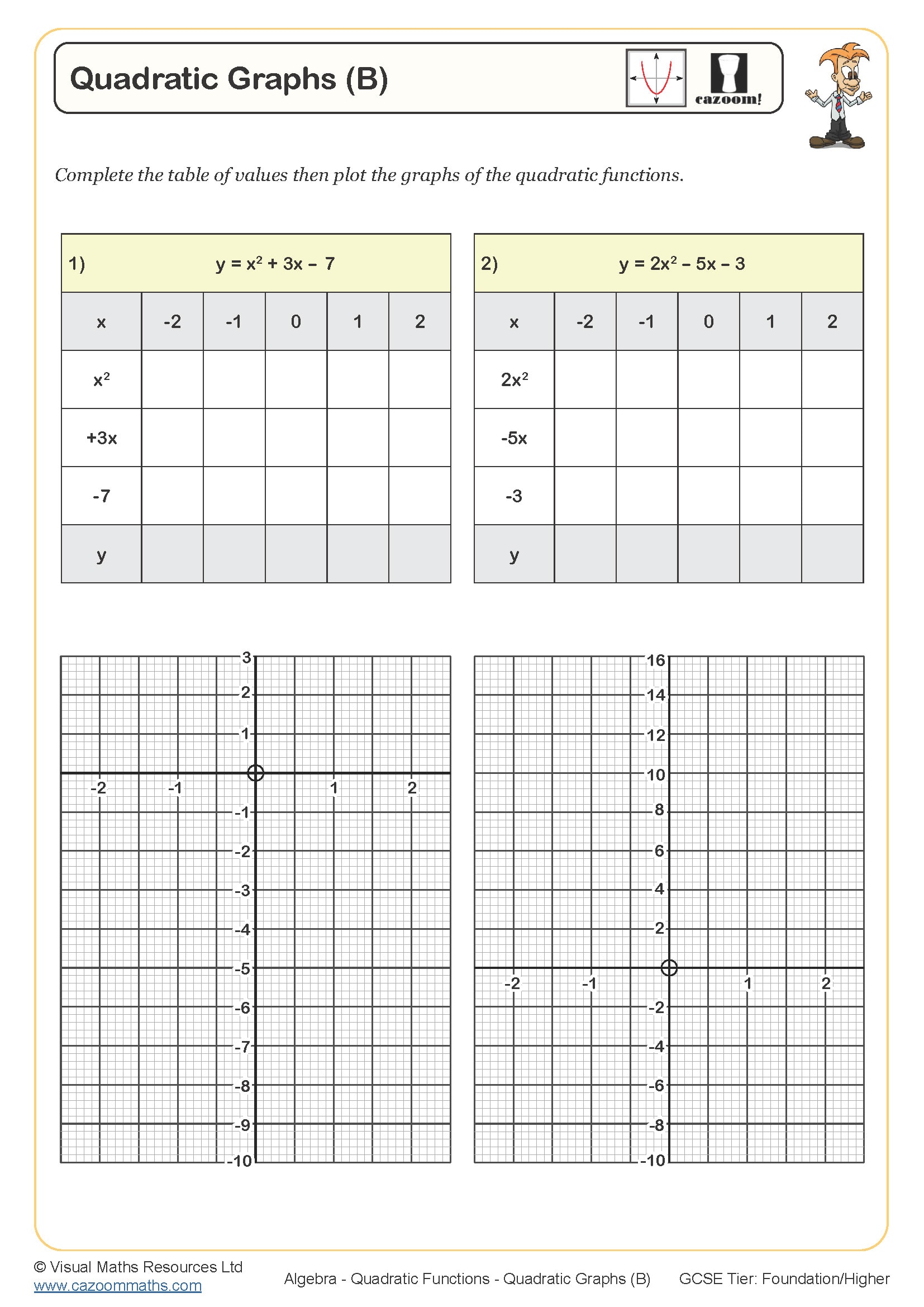
Quadratic Graphs (B)
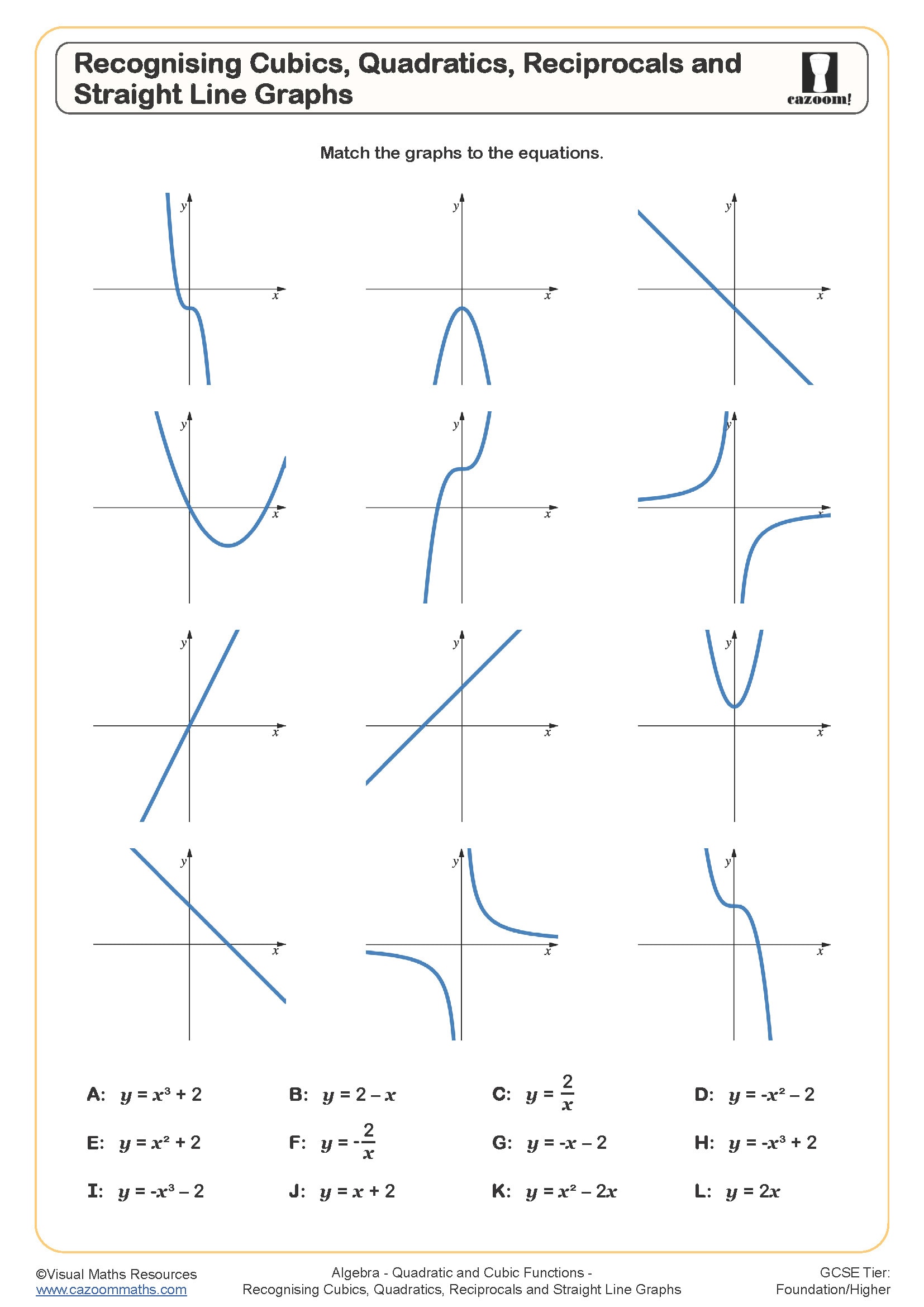
Recognising Cubics, Quadratics, Reciprocals and Straight Line Graphs
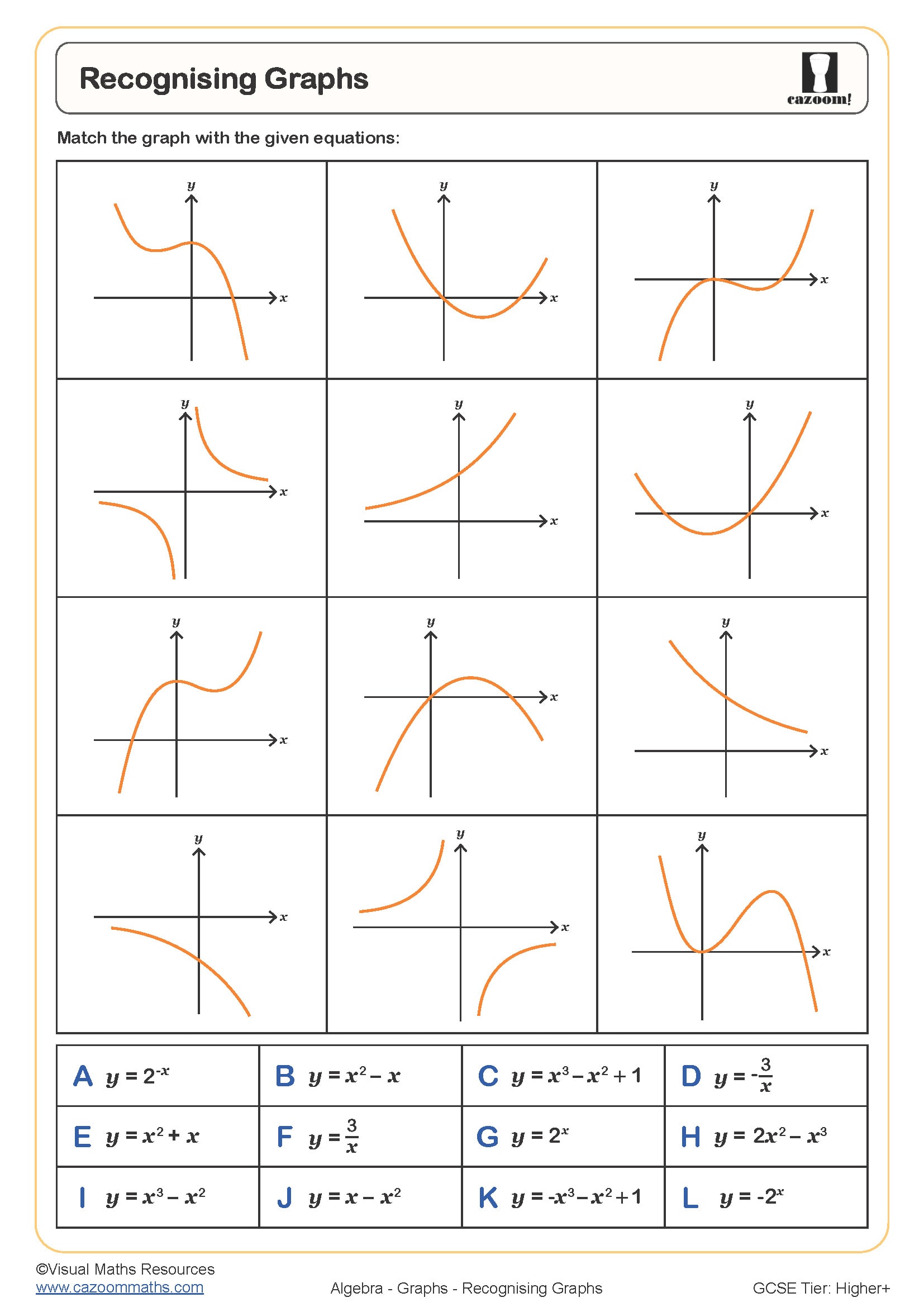
Recognising Graphs
Reflecting Graphs

Translating Graphs

Turning Points

All worksheets are created by the team of experienced teachers at Cazoom Maths.
Master Non-Linear Function Equations with Step-by-Step Practice Worksheets
Finding quality resources that properly explain nonlinear function equations isn't easy. We've created these worksheets to tackle the most common stumbling blocks students face. Each exercise includes detailed solutions showing the complete thinking process, from identifying nonlinear function examples to plotting complex curves. Perfect for homework, revision sessions, or cover lessons when you need reliable content.
Essential Skills Covered in These Year 11 Non-Linear Functions Worksheets
We've packed quite a lot into these worksheets! Students progress from recognising examples of nonlinear graphs to creating their own nonlinear function tables. The progression feels natural, starting with simple quadratic curves before moving to exponential and reciprocal functions. Students particularly enjoy the real-world examples that show where these mathematical concepts actually matter in everyday life.
Why Year 11 Students Need Targeted Non-Linear Functions Practice
Here's what we've noticed: students who regularly practice with linear and nonlinear function examples perform significantly better on GCSE assessments. The difference between understanding the theory and applying it confidently comes down to structured practice. These worksheets help students recognise patterns quickly and build the problem-solving confidence they'll need for A-Level mathematics.
Key benefits students gain from regular practice:
• Pattern recognition - Spot nonlinear relationships instantly in exam questions
• Graph interpretation - Read and analyse complex curves with confidence
• Equation manipulation - Transform nonlinear function equations efficiently
• Problem-solving speed - Complete GCSE questions within time constraints
• Conceptual understanding - Connect algebraic expressions to visual representations
Real-World Applications Where Students Use Non-Linear Functions
Students always ask, "When will I ever use this?" Here's the satisfying answer: Nonlinear functions appear everywhere in science, technology, and everyday life. From understanding population growth in biology to analysing profit curves in business studies, these mathematical tools are surprisingly practical. It's actually quite rewarding when students start spotting quadratic relationships in their physics experiments!
Specific applications students encounter:
• Physics coursework - Projectile motion and acceleration calculations
• Economics studies - Supply and demand curve analysis
• Computer science - Algorithm efficiency and growth rates
• Environmental science - Population dynamics and resource modelling
• Engineering projects - Structural load calculations and design optimisation
• Medical research - Drug concentration curves and dosage calculations