Menu

PRIMARYSECONDARYGCSE REVISION
SCHOOLSSEARCH
LOGINFREE TRIAL

KS3 Area Model Worksheets

Area model worksheets provide KS3 students with a visual approach to multiplication and algebraic expansion that builds number sense alongside procedural fluency. These resources help students understand the distributive property by breaking calculations into manageable rectangular sections, which proves particularly valuable when transitioning from numerical multiplication to expanding brackets with algebra. Teachers frequently notice that students who rely solely on column methods struggle when faced with algebraic expressions, whereas the area model creates a bridge between arithmetic and algebra that supports conceptual understanding. This collection spans Year 7 through Year 9, with each worksheet available as a PDF download and complete answer sheets included to support marking and student self-assessment.

Expanding Brackets and Simplifying - Using Algebra Tiles

Expanding Brackets and Simplifying - Using Algebra Tiles Worksheet Suitable for 8 and 9 Students

Expanding Double Brackets (A) Using the Grid Method

Expanding Double Brackets Worksheet fit for students in year 8, 9 and year 10

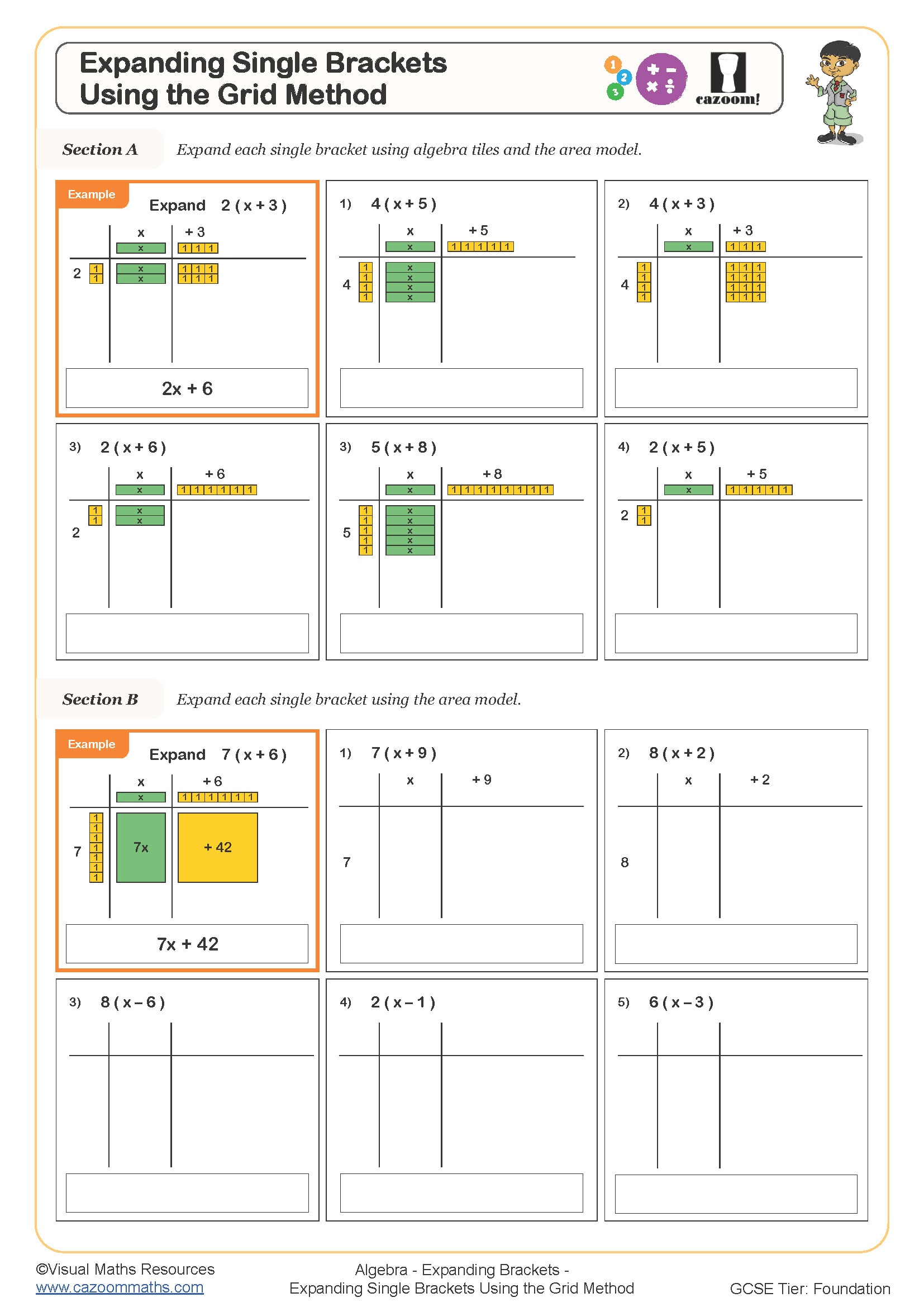
Expanding Single Brackets - Using the Grid Method

Expanding Single Brackets Worksheet perfect for students in year 8 and year 9

Factorising Using the Area Model

Factorising Using the Area Model Worksheet Suitable for Students in Year 8 and Year 9

Multiplying Fractions - Using the Area Model

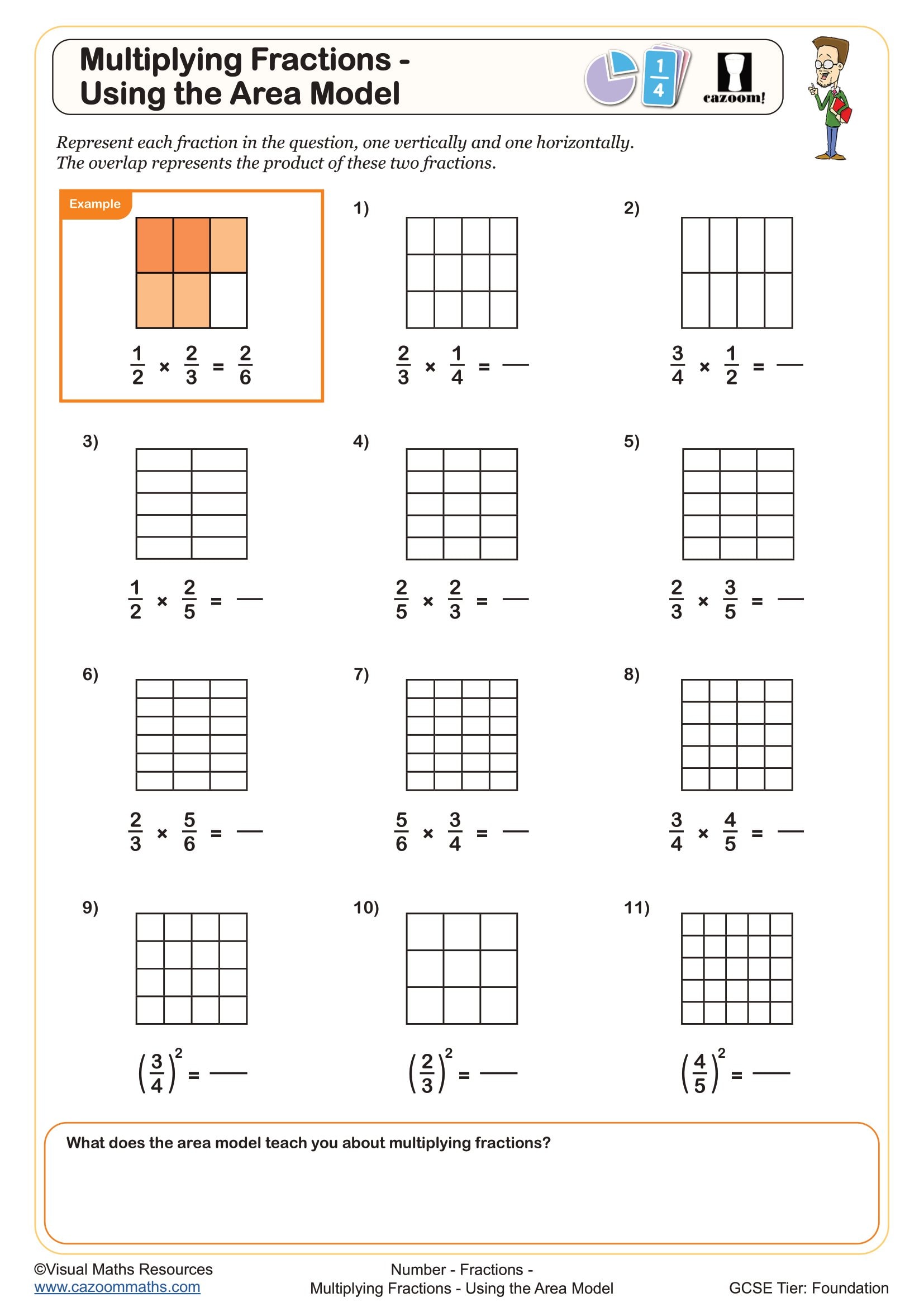
Multiplying Fractions - Using the Area Model Worksheet for Year 8 and Year 9 Students

Multiplying Unit Fractions - Using the Area Model

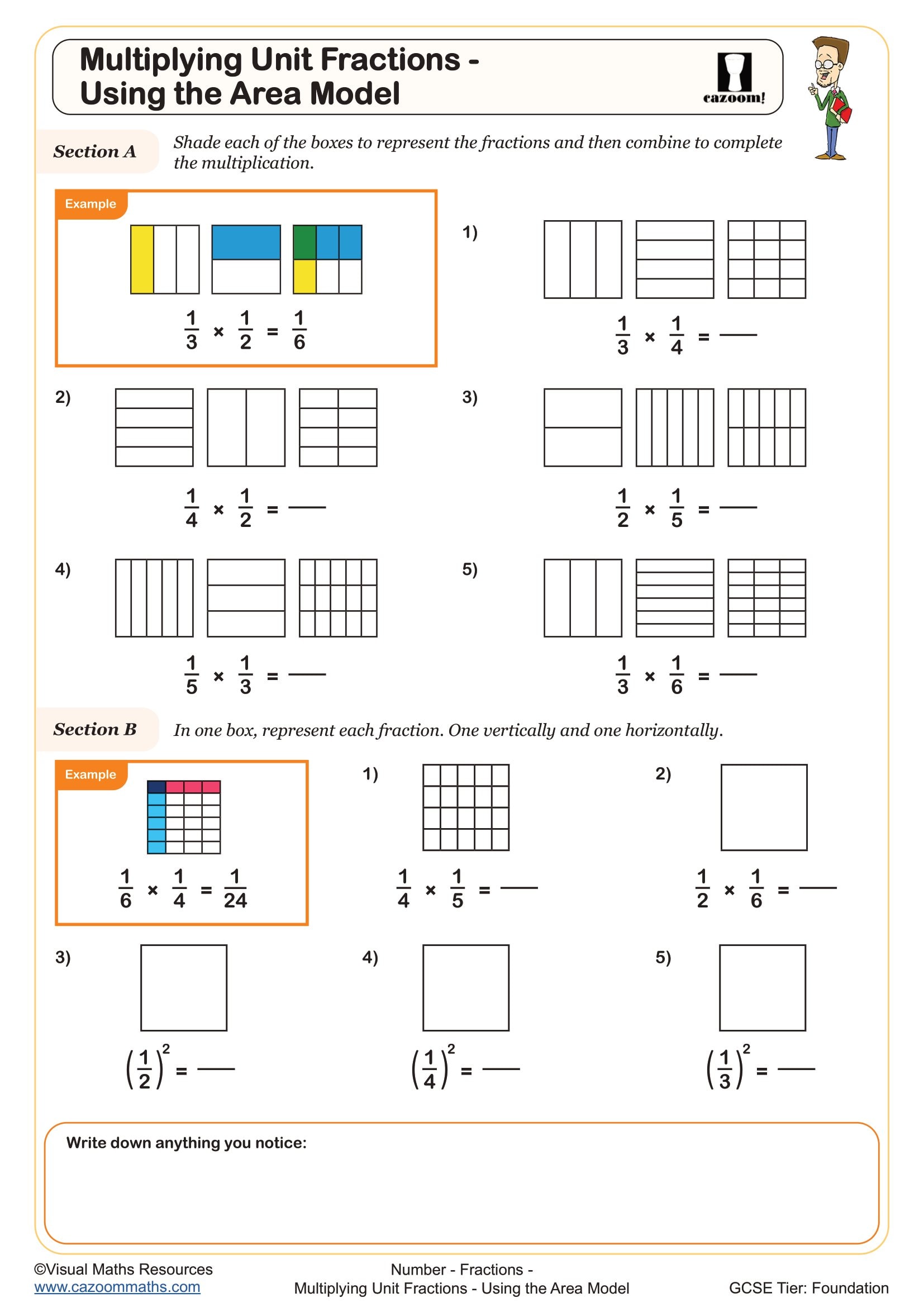
Multiplying Unit Fractions - Using the Area Model Worksheet Suitable for Year 8 and Year 9 Students

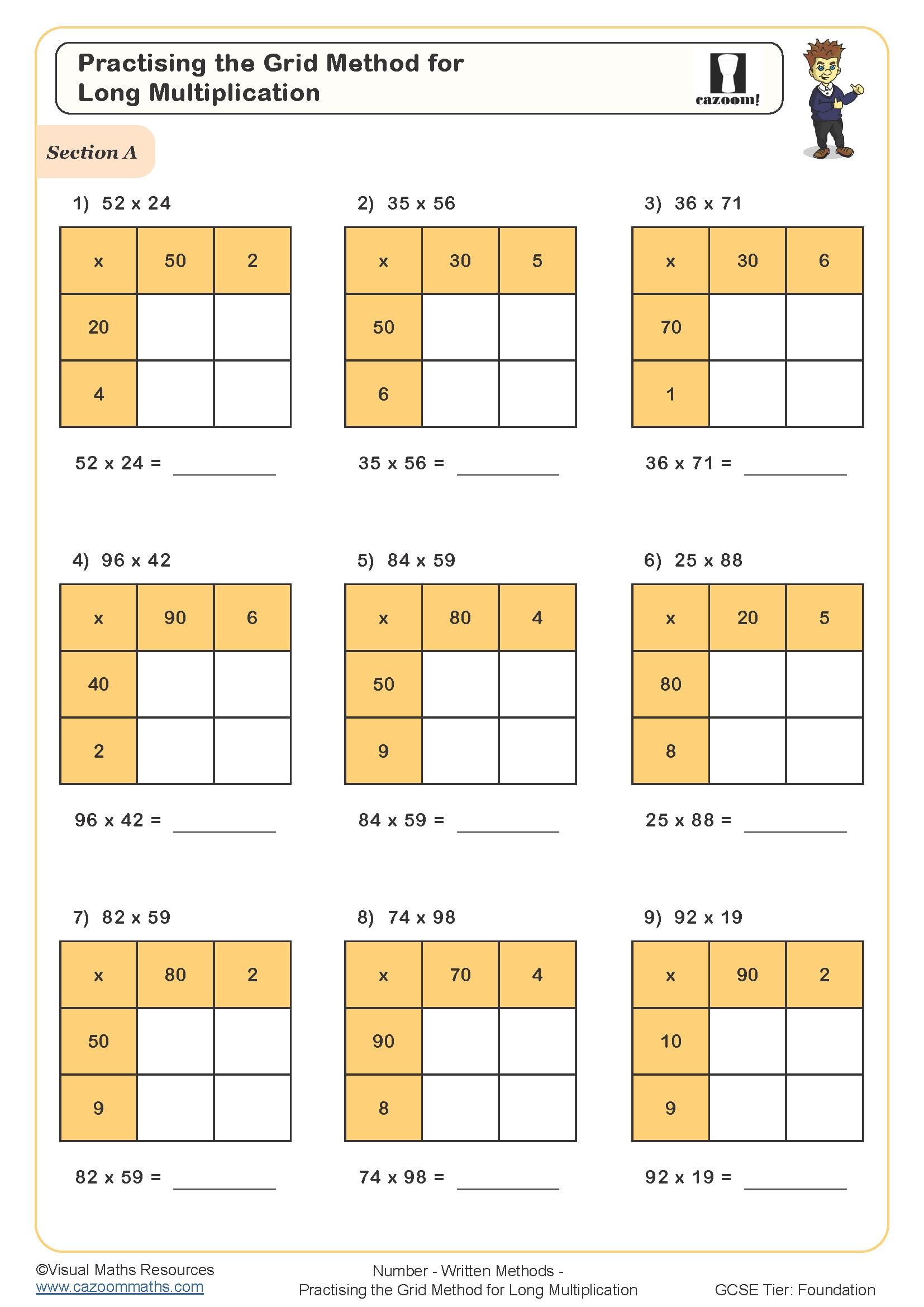
Practising the Grid Method for Long Multiplication

Long Multiplication Grid Method Worksheet created for students in KS3

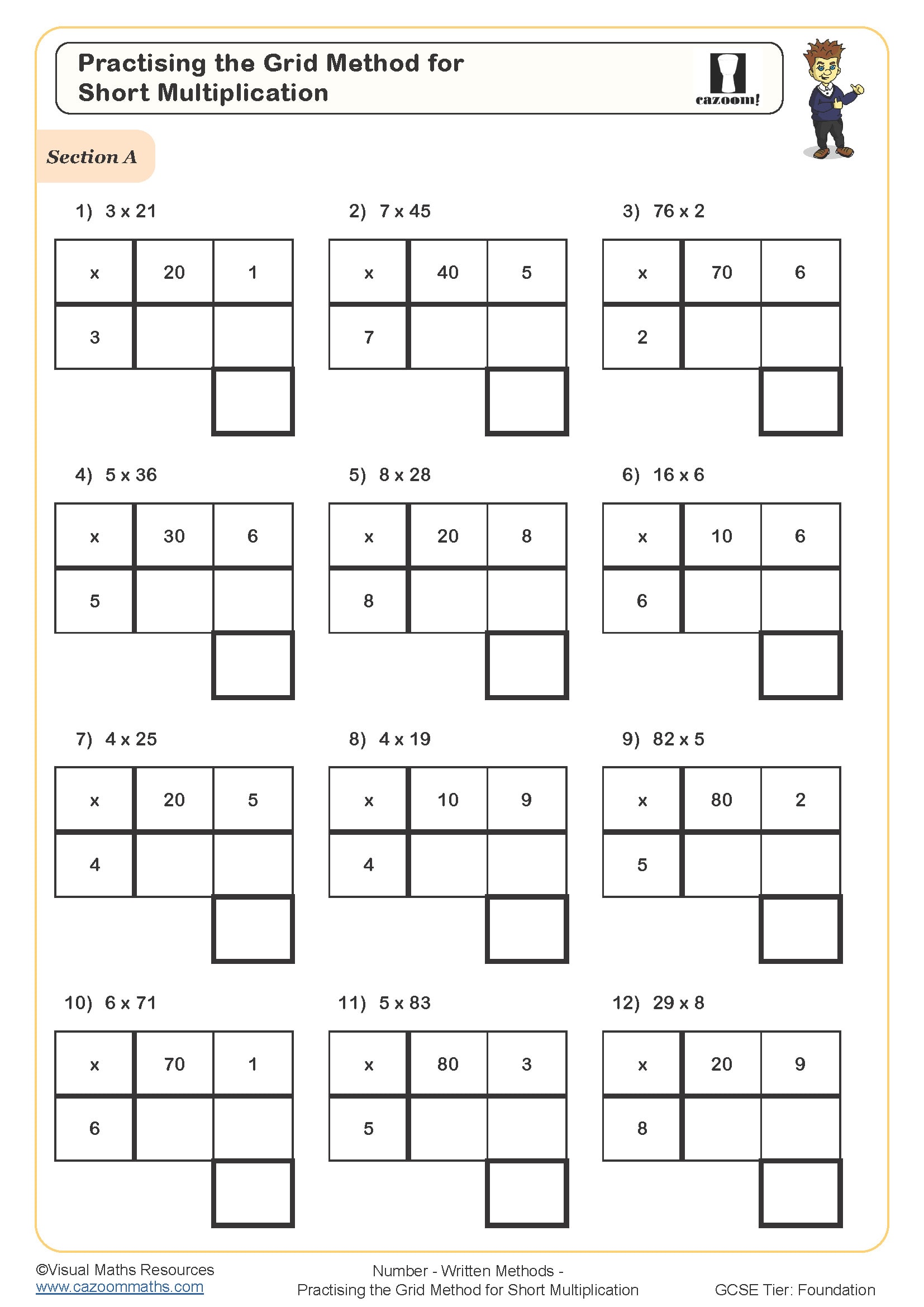
Practising the Grid Method for Short Multiplication (A)

Practising the Grid Method for Short Multiplication Worksheet suitable for students in KS3

All worksheets are created by the team of experienced teachers at Cazoom Maths.

What is the area model in maths?

The area model is a visual representation method where students partition rectangles to perform multiplication or expand algebraic expressions. Rather than relying on abstract algorithms, students draw a rectangle divided into sections that represent place values or algebraic terms, then calculate the area of each section before combining them. This approach aligns with the KS3 National Curriculum emphasis on multiplicative reasoning and forms the foundation for later work with quadratic expansion.

Teachers often observe that students who initially resist drawing the rectangles make significantly fewer sign errors when expanding brackets compared to those using FOIL or other mnemonic methods. The physical act of labelling each section helps students track positive and negative terms systematically, particularly when dealing with expressions like (x - 3)(2x + 5) where sign mistakes are common.

Which year groups use area model worksheets?

These area model worksheets cover Year 7, Year 8, and Year 9 across KS3. Students typically encounter the area model first in Year 7 when consolidating multi-digit multiplication, where it helps visualise calculations like 23 × 17 by breaking them into (20 + 3) × (10 + 7). This foundation prepares students for the transition to algebra in later Key Stage 3 work.

The progression across year groups reflects increasing complexity: Year 7 focuses on numerical applications and single bracket expansion, Year 8 introduces expanding double brackets with integers, whilst Year 9 extends to expressions involving negative coefficients and more complex algebraic terms. Many teachers find the area model particularly effective for lower-attaining Year 9 students who need a concrete method before attempting quadratic expansion questions that regularly appear on foundation GCSE papers.

How does the area model help with expanding brackets?

When expanding brackets using the area model, students create a rectangle with one factor labelling the width and the other the height, then subdivide it to show each term. For (x + 4)(x + 3), the rectangle splits into four sections: x², 3x, 4x, and 12. Students calculate each area separately, then combine like terms to reach x² + 7x + 12. This visual approach makes the distributive property explicit rather than relying on memorisation.

This method connects directly to real-world applications in design and construction, where calculating areas of composite shapes requires similar partitioning skills. Architects and engineers regularly decompose irregular floor plans into rectangles to calculate materials needed, whilst landscape designers use area breakdowns to cost different sections of gardens. Understanding that algebraic expansion follows the same logic as calculating physical areas helps students recognise maths as a practical tool rather than abstract symbol manipulation.

How can teachers use these area model worksheets effectively?

The worksheets provide structured progression from guided examples with pre-drawn rectangles through to questions where students must construct their own area models. Early questions typically include partially completed grids to scaffold the process, whilst later problems remove this support to develop independence. The answer sheets show complete working, allowing students to identify exactly where errors occur in their own solutions rather than simply checking final answers.

Many teachers use these resources during intervention sessions with students who struggle with algebraic manipulation, as the visual nature helps identify whether difficulties stem from conceptual misunderstanding or calculation errors. The worksheets also work well for paired activities where one student constructs the area model whilst the other verifies dimensions and calculations, promoting mathematical discussion. For homework, the clear structure means parents can support their child even without strong algebraic knowledge, as the rectangular approach makes the process more accessible than traditional methods.