KS3 Expanding Brackets Worksheets
What Are KS3 and KS4 Expanding Brackets Worksheets?
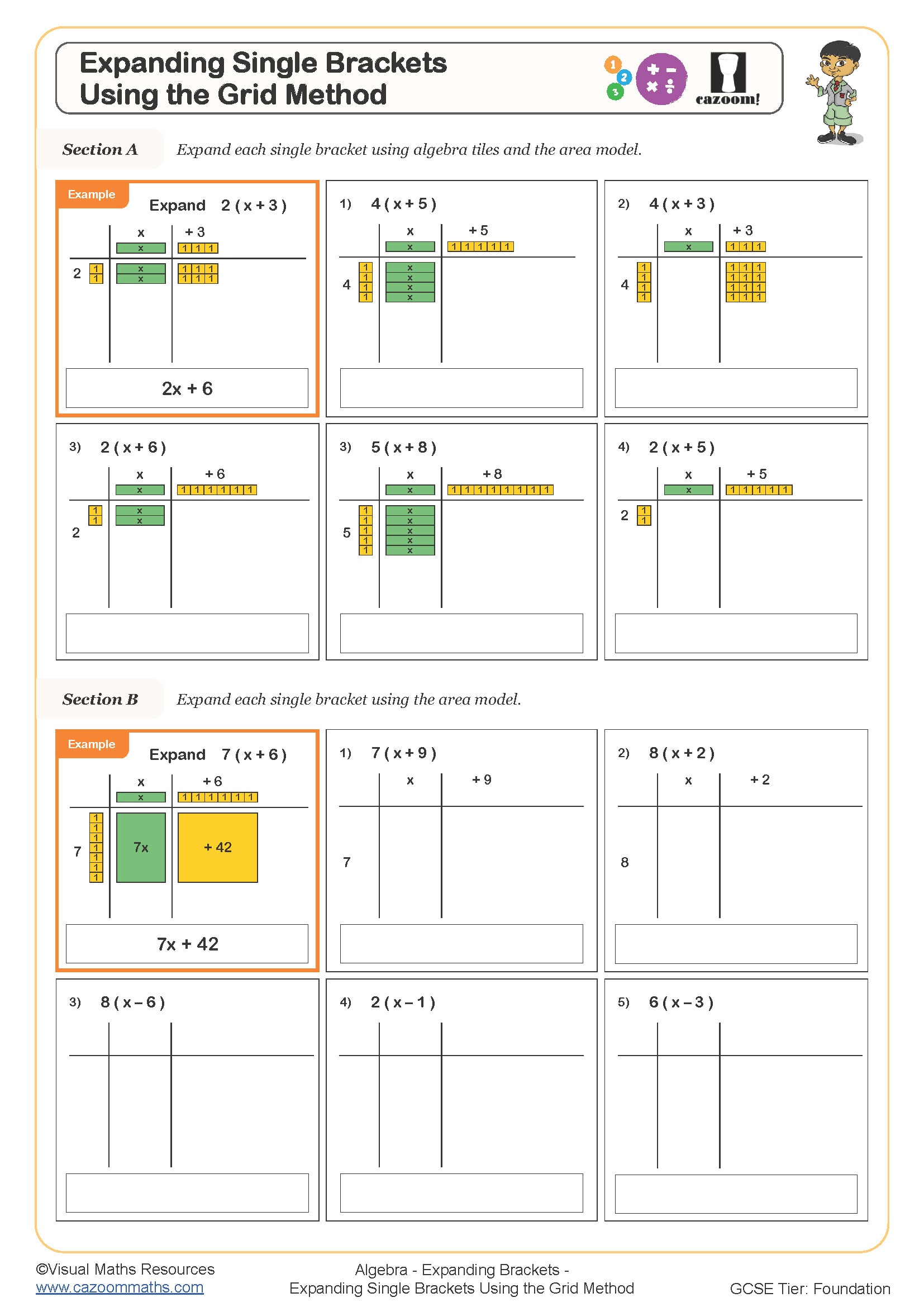
KS3 and KS4 expanding brackets worksheets provide targeted practice in using the distributive law to multiply terms across brackets. At KS3, this begins with single brackets containing two terms, such as 3(x + 4), before progressing to expressions with subtraction, negative multipliers, and brackets involving multiple variables. The skills developed here directly support GCSE content, where students encounter double brackets, perfect squares, and the difference of two squares.
Students frequently lose marks in assessments when they forget to multiply every term inside the bracket by the term outside. A typical error involves expanding 5(2x - 3) as 10x - 3 rather than 10x - 15. Worksheets that systematically address this by including varied examples with both positive and negative multipliers help students develop accuracy before moving to more demanding algebraic work.
Which Year Groups Study Expanding Brackets?
Expanding brackets appears in the KS3 National Curriculum and is typically introduced in Year 8, where students first encounter single bracket expansion as part of their work on algebraic manipulation. Year 9 students revisit and extend this skill, working with more complex expressions and beginning to connect expansion with factorising as inverse operations. This topic forms essential groundwork for GCSE algebra, where it underpins solving quadratic equations and manipulating formulae.
The progression across these year groups moves from concrete numerical examples to increasingly abstract algebraic forms. Year 8 students might expand 4(a + 5) or -2(3b - 7), whilst Year 9 worksheets introduce brackets containing fractional or decimal coefficients, expressions requiring simplification after expansion, and preparation for expanding double brackets. Teachers often find that regular low-stakes practice at each stage prevents students from carrying misconceptions forward into GCSE work.
Why Does Simplifying After Expanding Brackets Matter?
Simplifying algebraic expressions after expanding brackets teaches students to recognise and combine like terms, a skill that extends well beyond this isolated topic. When expanding something like 3(2x + 1) + 5x, students must first apply the distributive law to get 6x + 3 + 5x, then collect like terms to reach the simplified form 11x + 3. This two-stage process requires careful attention to both the structure of expressions and the arithmetic involved.
This skill has direct applications in physics and engineering, where formulae often require manipulation before substitution. When calculating the area of composite shapes or working with scientific equations like v = u + at, students frequently need to expand brackets and simplify before evaluating expressions. The algebraic fluency developed through these worksheets enables students to rearrange complex formulae confidently, a requirement across STEM subjects at GCSE and beyond.
How Can Teachers Use These Worksheets in Lessons?
The worksheets provide scaffolded practice that allows students to build confidence with expanding brackets before attempting more complex algebraic problems. Starting with straightforward examples and gradually introducing negative terms, fractional coefficients, and expressions requiring simplification means students develop accuracy at each stage. The inclusion of answer sheets enables immediate feedback, which research shows significantly improves retention when students correct their own mistakes promptly.
Many teachers use these resources for targeted intervention with students who struggle during whole-class teaching, as the structured format allows learners to work at their own pace. They work equally well as homework to consolidate lesson content or as starter activities to retrieve prior knowledge before introducing factorising. Paired work, where one student expands whilst another checks against the answer sheet, helps develop mathematical communication and allows students to articulate the steps involved in applying the distributive law.