KS3 Fractions Decimals Percentages Worksheets

This collection of fractions decimals percentages worksheets helps students master the essential conversions and equivalences that underpin much of Key Stage 3 mathematics. Students practise converting between all three forms, calculating percentages of amounts, and recognising equivalent values across representations. Teachers often notice that whilst students can perform isolated conversions, they struggle to select the most efficient method when presented with mixed questions, particularly when deciding whether to convert to fractions or decimals first. Each worksheet downloads as a PDF with complete answer sheets included, making them suitable for both classroom teaching and independent revision. The fractions and percentages worksheets year 8 materials bridge the gap between basic conversions and the more demanding problem-solving contexts required at GCSE.

Colourful Equivalences (A)

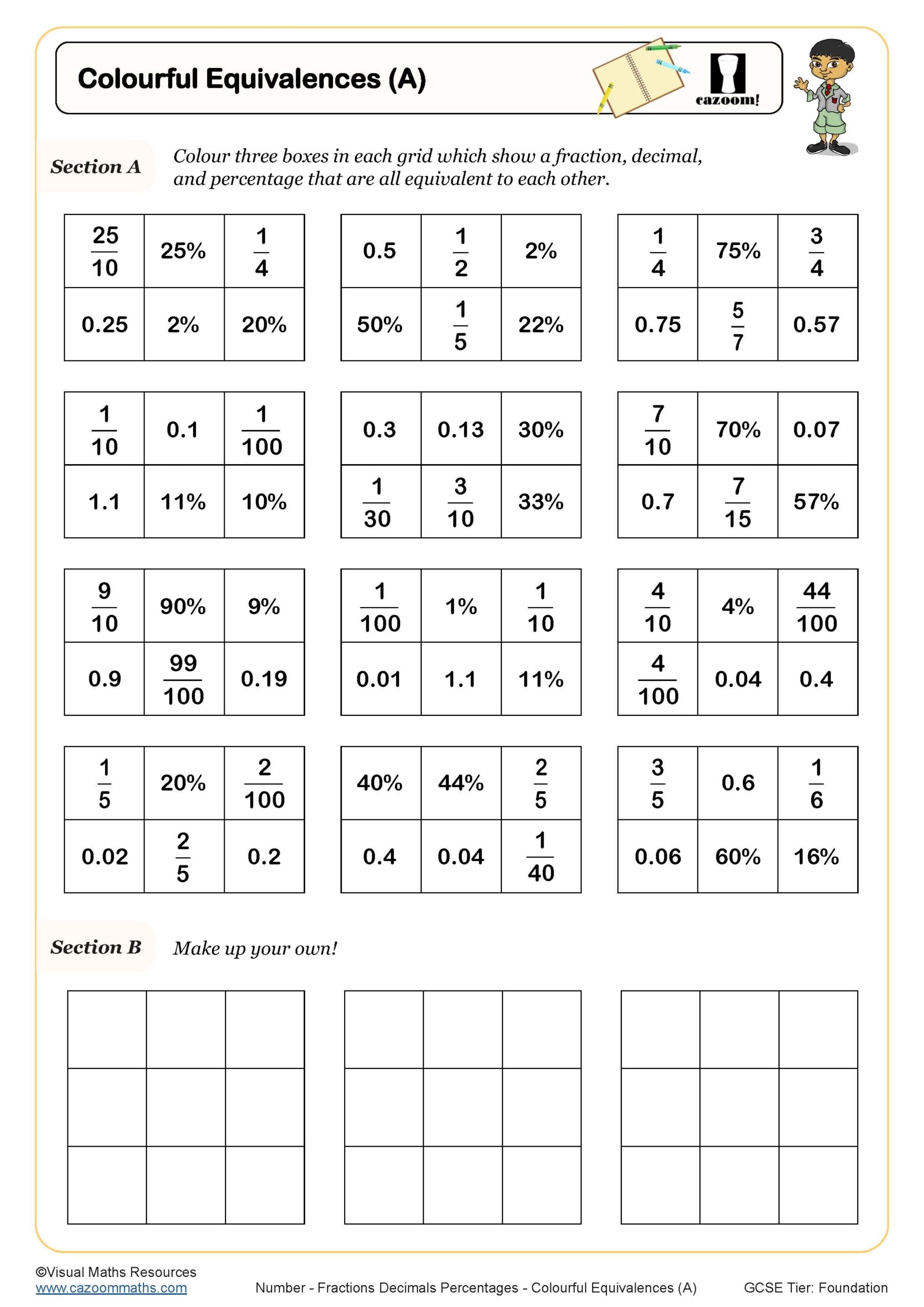
Colourful Equivalences (B)

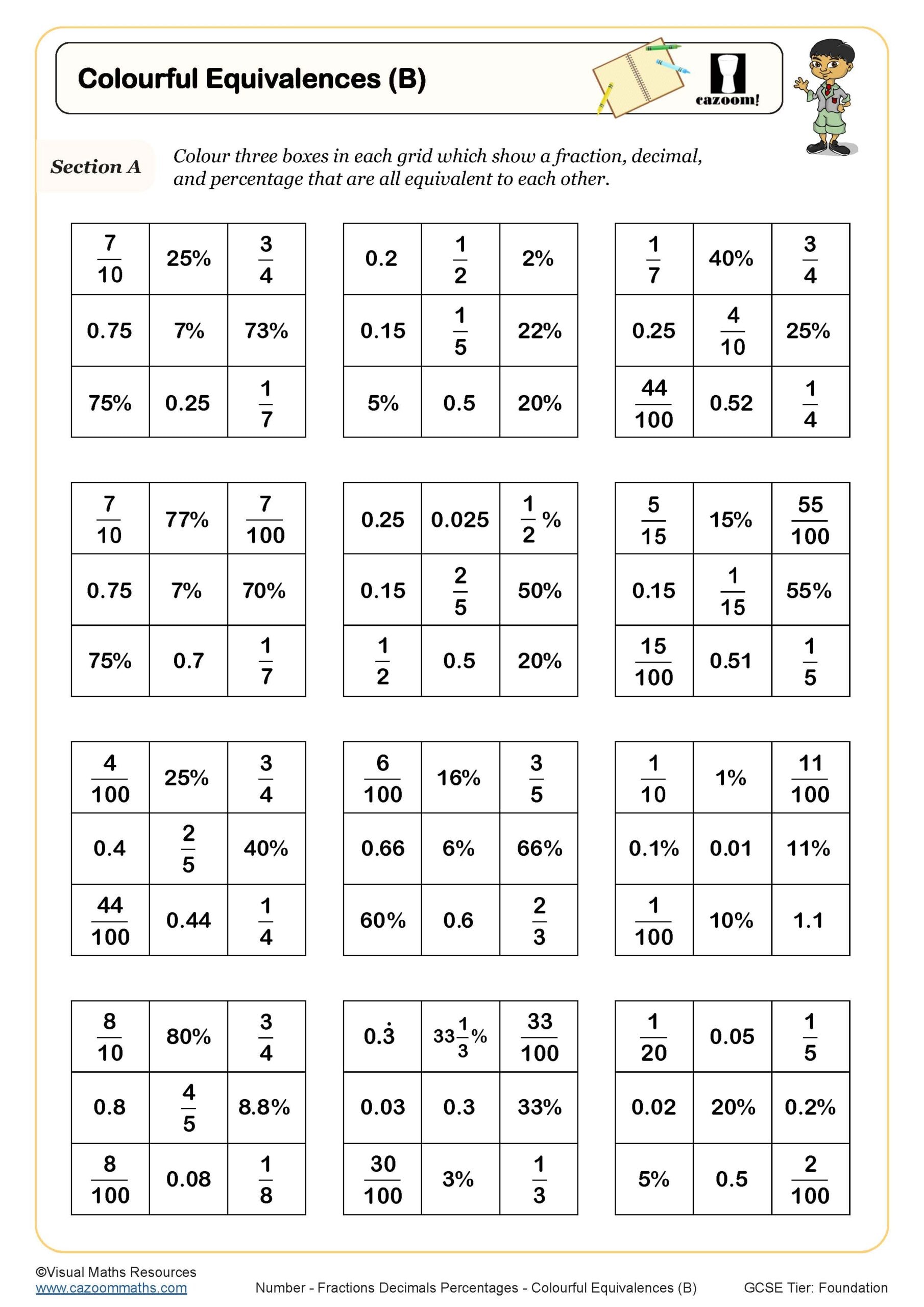
Equivalence Search (B)

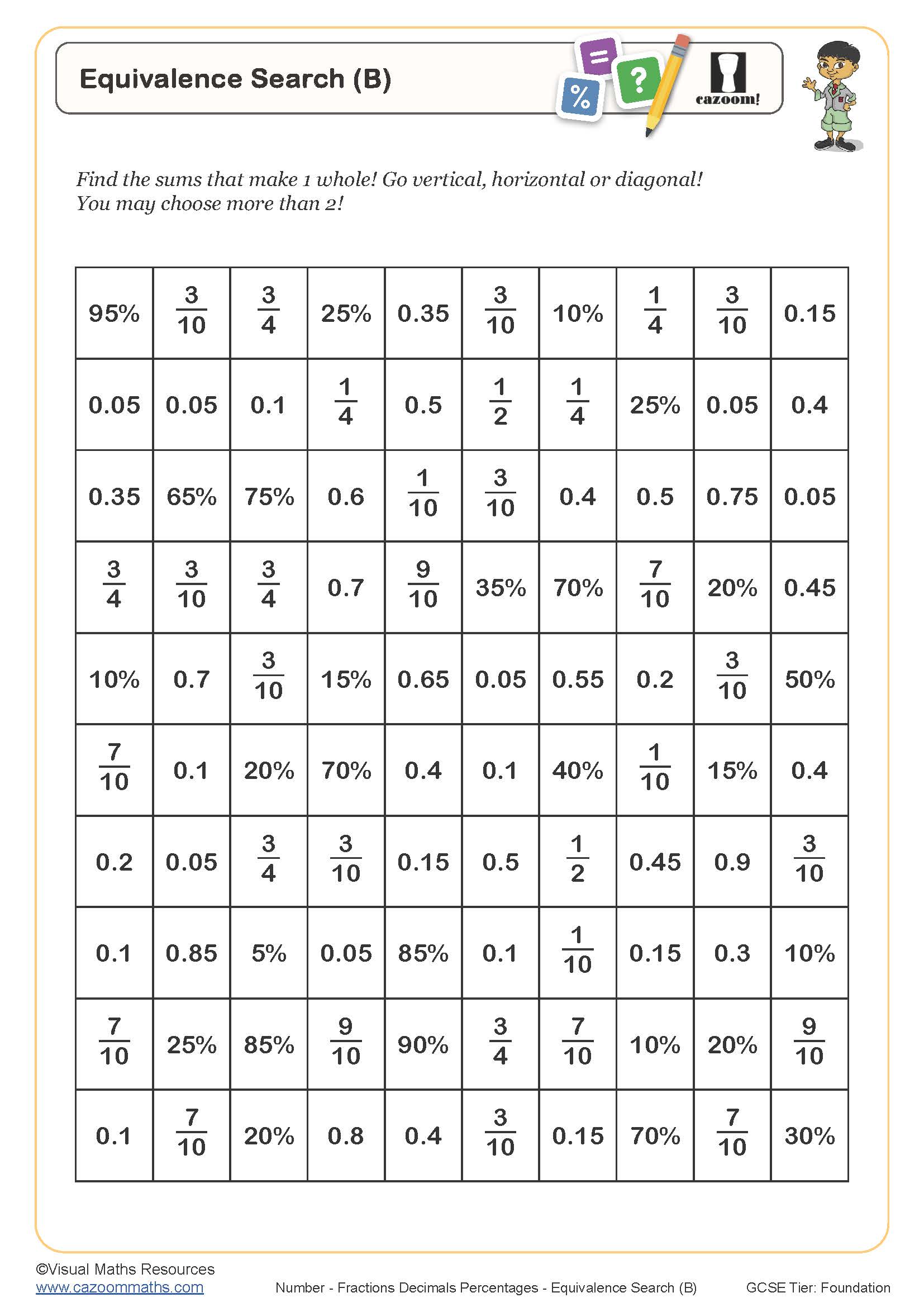
Equivalence Search (C)

FDP Problem Solving

Fractions Decimals Percentages (A)

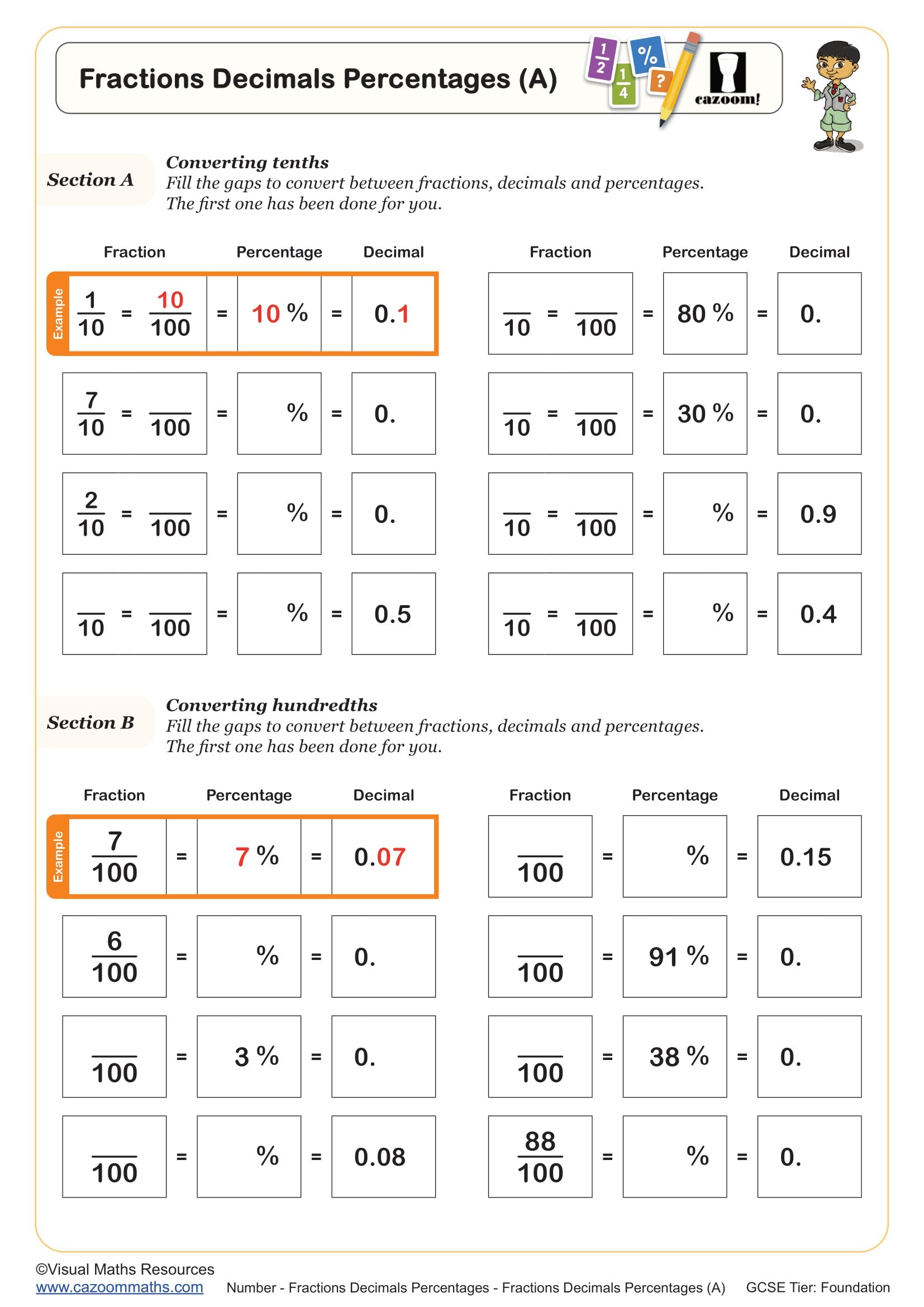
Fractions Decimals Percentages (B)

Ordering Fractions Decimals and Percentages (A)

Ordering Fractions Decimals and Percentages (B)

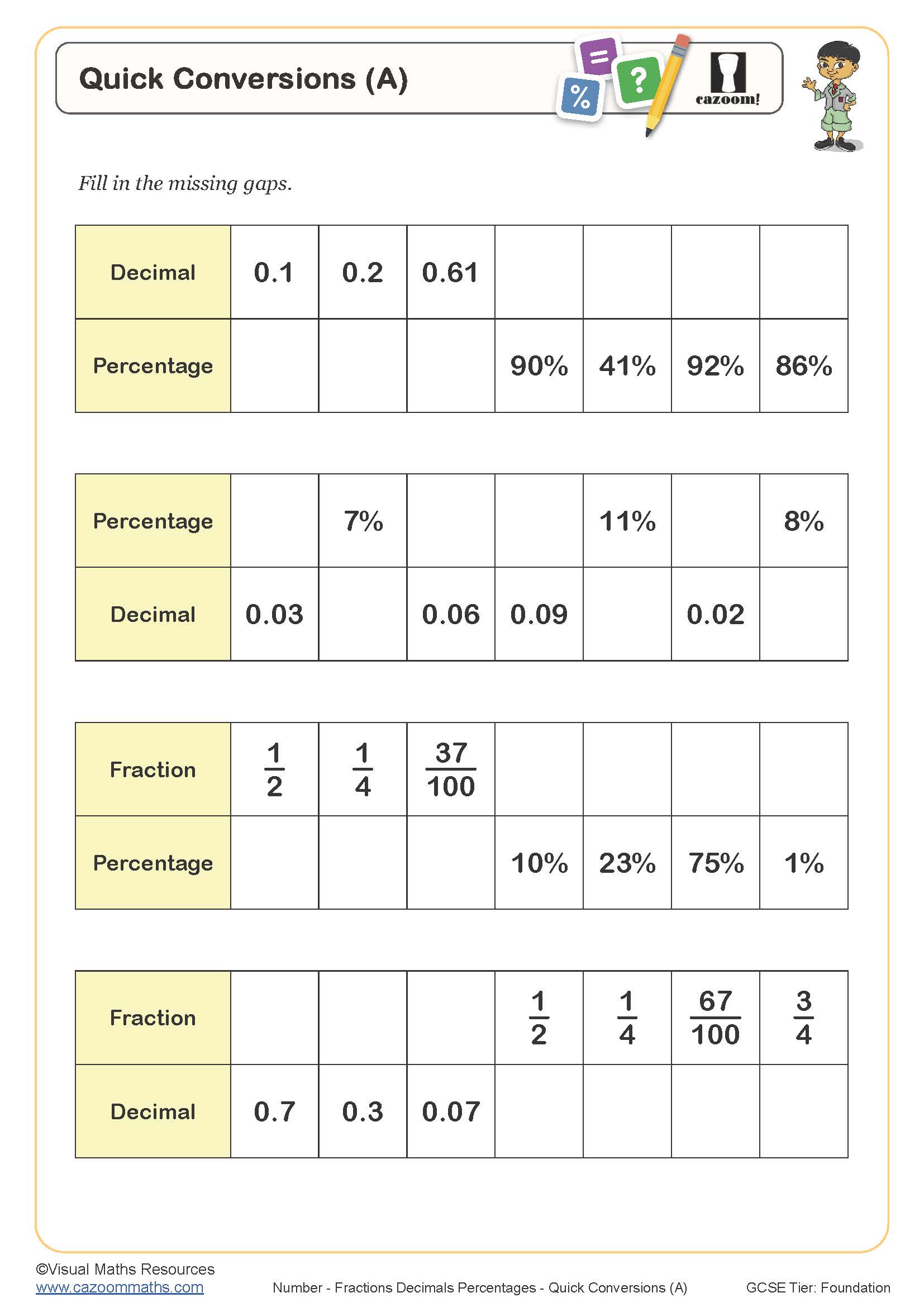
Quick Conversions (A)

Writing Rational Numbers as Decimals

What should students focus on when working with fractions and percentages worksheets year 8?

Year 8 students should concentrate on fluency with conversions in both directions, understanding that 0.35 = 35% = 7/20 are equivalent representations of the same value. The worksheets develop this fluency through repeated practice whilst introducing more complex applications such as percentage increase and decrease, and comparing values across different forms. Teachers frequently observe that students can convert fractions to decimals successfully but make errors when converting recurring decimals back to fractions, often forgetting the algebraic method or misapplying the place value approach.

Another common difficulty arises with ordering mixed sets of fractions, decimals and percentages. Students lose marks in assessments when they fail to convert all values to the same form before comparing, or when they make sign errors during conversions. The worksheets provide systematic practice in these comparison questions, helping students develop the habit of choosing one consistent form before attempting to order values.

Which year groups use these fractions decimals percentages worksheets?

These worksheets support Year 7, Year 8 and Year 9 students throughout Key Stage 3. The topic appears early in Year 7 where students revisit and consolidate primary school knowledge of simple conversions, then progresses through increasingly complex applications. Year 7 focuses on converting between simple fractions like halves, quarters and fifths alongside their decimal and percentage equivalents, building the foundations for all later work.

By Year 8, students tackle non-calculator methods for converting complex fractions to decimals and percentages, whilst Year 9 worksheets incorporate recurring decimals, reverse percentage problems and multi-step questions that combine several conversion skills. The progression reflects the National Curriculum's expectation that students develop both procedural fluency and the ability to select appropriate methods for different problem types, preparing them for GCSE questions that embed these skills within broader contexts.

How do students convert recurring decimals to fractions?

Converting recurring decimals to fractions requires an algebraic approach that students first encounter in Year 8 or Year 9. The method involves setting the recurring decimal equal to x, multiplying by an appropriate power of 10 to shift the recurring part, then subtracting the original equation to eliminate the recurring digits. For example, for 0.7̇, students set x = 0.777..., multiply by 10 to get 10x = 7.777..., then subtract to find 9x = 7, giving x = 7/9. Many students initially find this counterintuitive because they're used to arithmetic methods rather than algebraic manipulation for conversions.

This skill connects directly to rational number theory in higher mathematics and computer science, where understanding how numbers are represented matters enormously. In programming, floating-point arithmetic can produce unexpected results because computers store decimals in binary form, and some fractions that terminate in base 10 (like 0.1) actually recur in binary. Financial software engineers must understand these conversions thoroughly to avoid rounding errors in currency calculations, where even tiny discrepancies across millions of transactions create significant problems.

How can teachers use these worksheets effectively in lessons?

The worksheets work well as structured practice following direct teaching of conversion methods, with answer sheets allowing students to self-check their working and identify where errors occur. Teachers can use them diagnostically to pinpoint whether difficulties stem from procedural mistakes (like incorrect place value) or conceptual misunderstandings about equivalence. The graduated difficulty within each worksheet supports mixed-ability teaching, as students can attempt increasingly challenging questions whilst working from the same resource.

Many teachers find these worksheets valuable for intervention sessions with students who need additional practice before assessments, or as homework to reinforce classroom learning. They're particularly effective when used alongside paired work, where students can explain their conversion method choices to each other, as this verbalisation often reveals misconceptions that silent practice might miss. The complete answer sheets also make the worksheets suitable for cover lessons or independent study periods where immediate teacher feedback isn't available.