KS3 Negative Numbers Worksheets
Calculations Crossing Zero (A)

Calculations Crossing Zero (B)

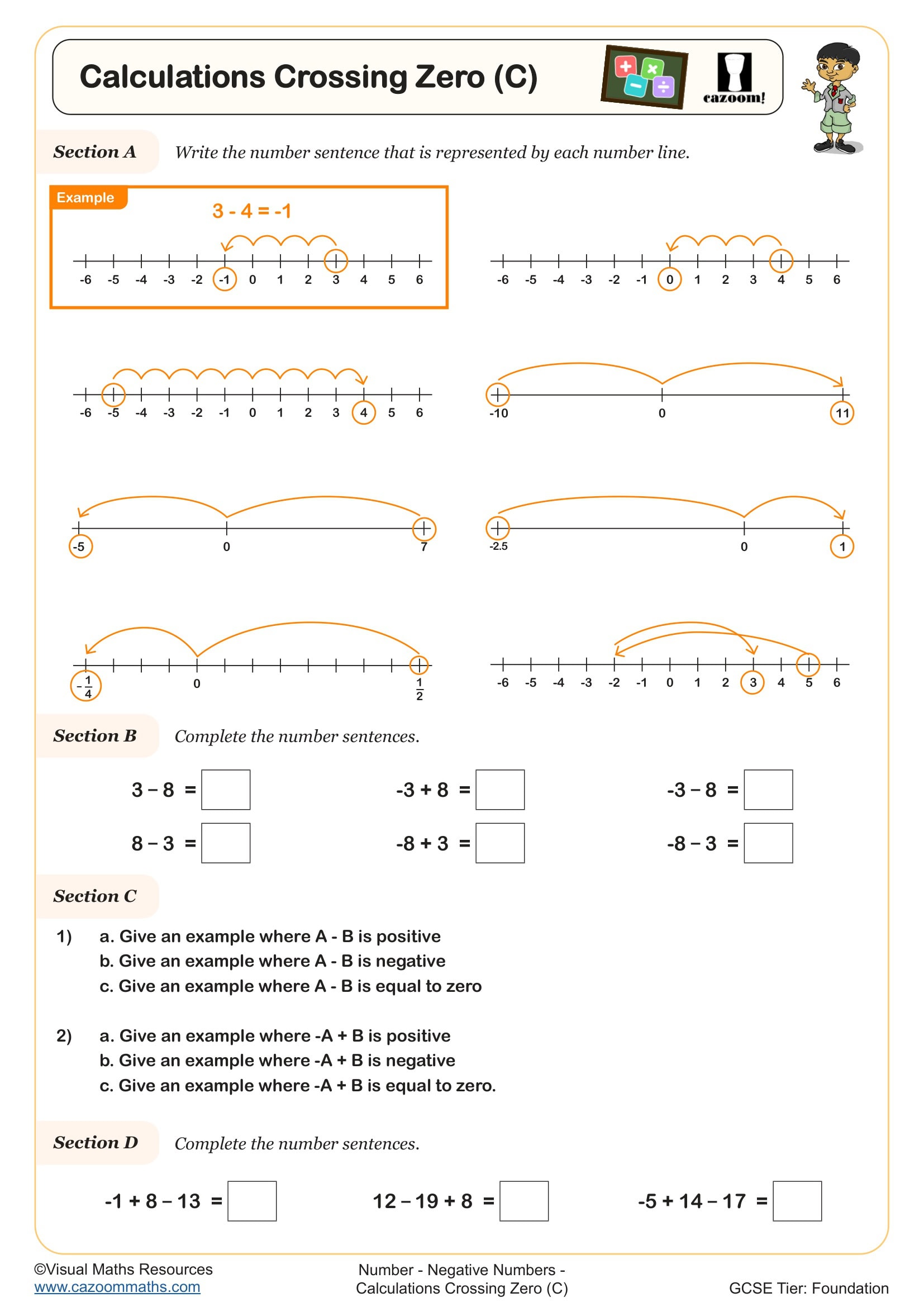
Calculations Crossing Zero (C)
Comparing Negative Numbers

Comparing Temperatures

Directed Number - Addition Using Directed Counters

Directed Number - Multiplication Using Directed Number Counters

Directed Number - Subtraction Using Directed Counters

Directed Number – Addition by Pattern Spotting

Directed Number – Subtraction by Pattern Spotting

Finding the Difference - Directed Numbers

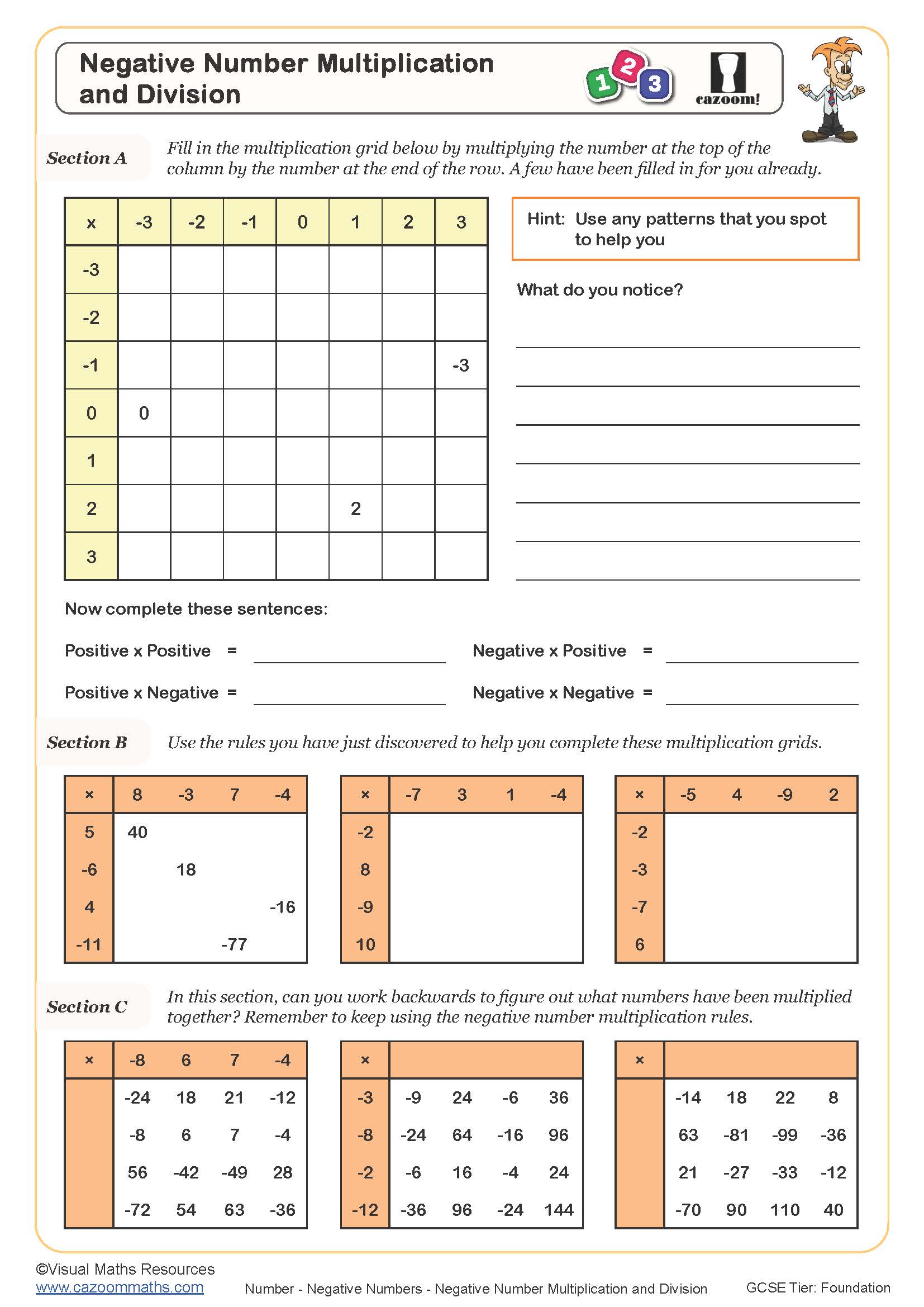
Negative Number Multiplication and Division
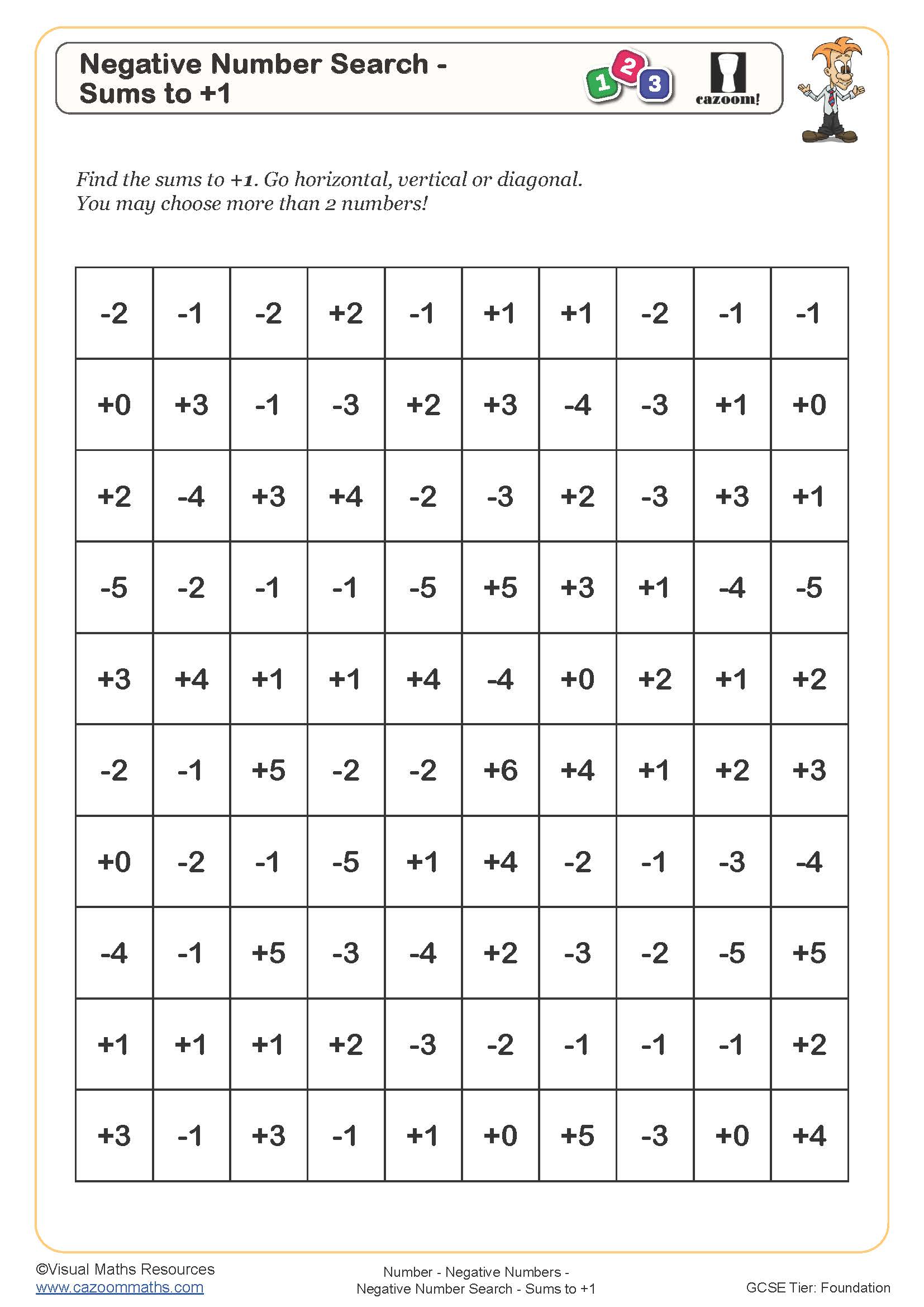
Negative number search - sums to +1
Negative Numbers - 4 Operations Puzzles

Negative Numbers 10 Minute Challenge

Practice Negative Number Addition and Subtraction

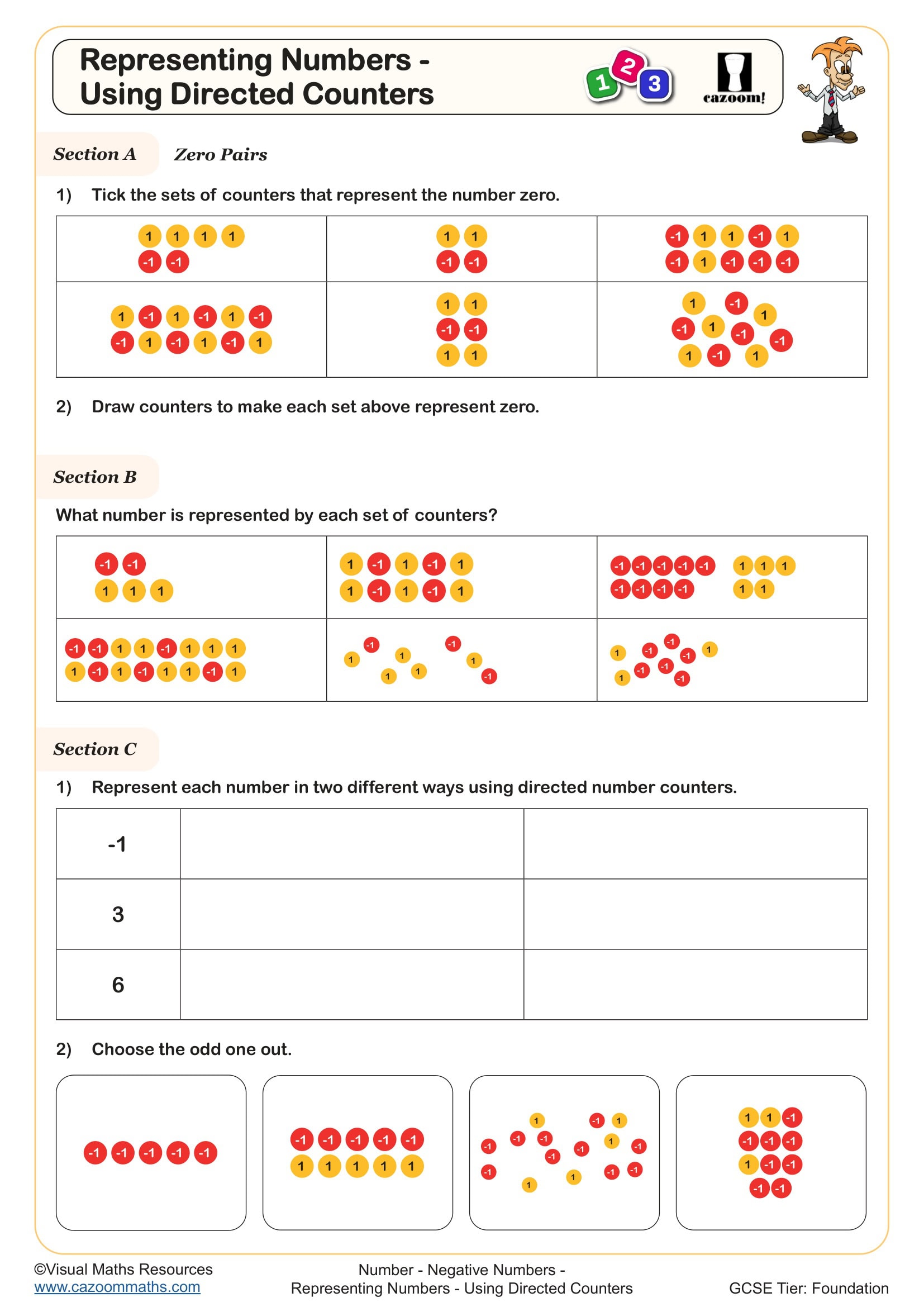
Representing Numbers - Using Directed Counters
What are directed numbers and why do students struggle with them?
Directed numbers are integers that include both positive and negative values, along with zero. The term emphasises that numbers have direction on the number line, moving either above or below zero. In the National Curriculum, students encounter directed numbers formally from Year 7 onwards, though some meet negative values earlier through contexts like temperature or bank balances.
A persistent misconception occurs when students treat two negative signs as simply making a positive without understanding why. When calculating 5 − (−3), many students write 2 instead of 8 because they see the two minuses and subtract. Teachers often find that using a number line helps students visualise why subtracting a negative number means moving in the positive direction, though this visual scaffold needs revisiting regularly as calculations become more abstract.
Which year groups study negative numbers at KS3?
These worksheets cover Year 7, Year 8, and Year 9, reflecting how negative number work develops throughout KS3. Students meet the fundamentals of ordering and adding negative numbers in Year 7, building on any informal encounters from upper KS2. By Year 8, expectations include confident handling of all four operations with negative integers, including multi-step problems.
The progression across these year groups moves from concrete contexts towards abstract calculations. Year 7 worksheets typically include number lines and temperature scenarios as visual supports. Year 8 resources introduce more complex mixed operations and require students to determine the correct order of operations when negative numbers appear. Year 9 materials often present algebraic contexts where negative number facility becomes essential for manipulating expressions and solving equations.
How do multiplication and division rules work with negative numbers?
The rules for multiplying and dividing negative numbers follow consistent patterns: two numbers with the same sign produce a positive result, whilst numbers with different signs produce a negative result. So −3 × −4 = 12 (both negative gives positive), but −3 × 4 = −12 (different signs give negative). Students need to learn these rules securely because exam mark schemes frequently penalise sign errors even when the numerical calculation is correct.
These rules connect directly to real-world applications in science and finance. In physics, velocity direction uses negative numbers to indicate backwards motion, so multiplying negative velocity by negative time makes mathematical sense of rewinding footage. In business contexts, multiplying a negative price change (discount) by a negative quantity (items returned) results in a positive value added back to accounts. Understanding why the rules work, rather than just memorising them, helps students apply negative numbers across STEM subjects.
How can these worksheets support students who find negative numbers difficult?
The worksheets provide scaffolded practice that builds from ordering exercises through to increasingly complex calculations with all four operations. Many include number line diagrams or visual models in earlier questions before moving to abstract problems, allowing students to develop conceptual understanding alongside procedural fluency. The variety within the collection means teachers can select resources matched to specific gaps, whether that's uncertainty about subtraction or persistent multiplication errors.
These materials work effectively for intervention groups where students need focused revision before tackling algebra or GCSE topics that assume negative number competence. Teachers often use them for homework following initial teaching, as the included answer sheets let students check their work independently. In mixed-ability classes, they're useful for paired work where students can explain their reasoning to each other, which often reveals whether they're applying rules mechanically or genuinely understanding the mathematics behind directed number calculations.