KS4 Factorising Worksheets

These KS4 factorising worksheets give students structured practice across essential factorising techniques needed for GCSE success. The collection covers factorising quadratics, expressions with common factors, and more challenging algebraic forms that appear throughout higher-tier exam papers. Teachers frequently notice that students who can expand brackets confidently often reverse the process incorrectly when factorising, particularly when dealing with negative coefficients or missing middle terms. Each worksheet downloads as a PDF with complete answer sheets included, allowing students to check their working independently and identify where errors occur. The worksheets progress from single-method questions to mixed problems that mirror exam-style questions, building the fluency students need to recognise which factorising approach each expression requires.

Difference of Two Squares

Expanding and Factorising Mixed Exercise

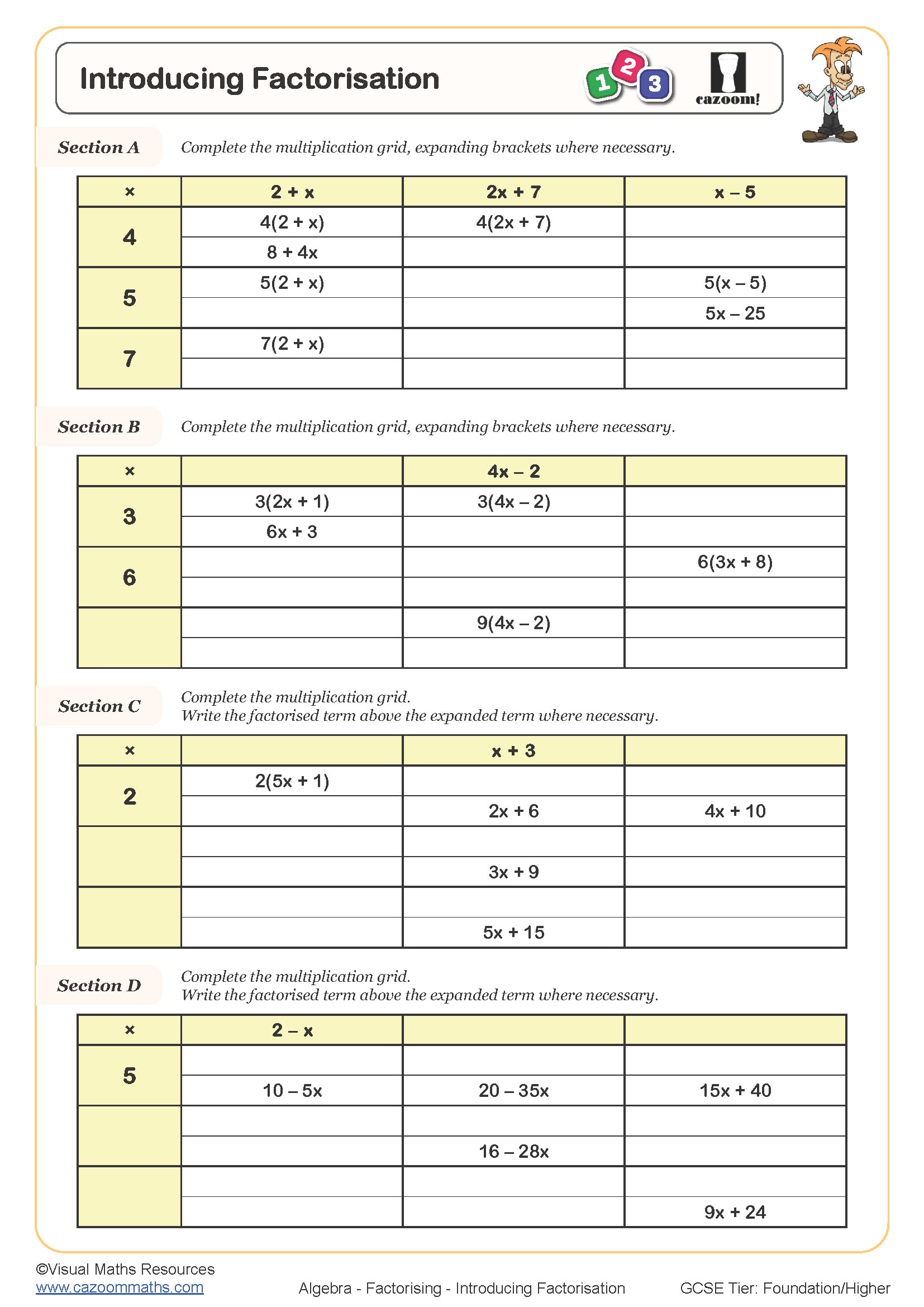
Factorising Expressions

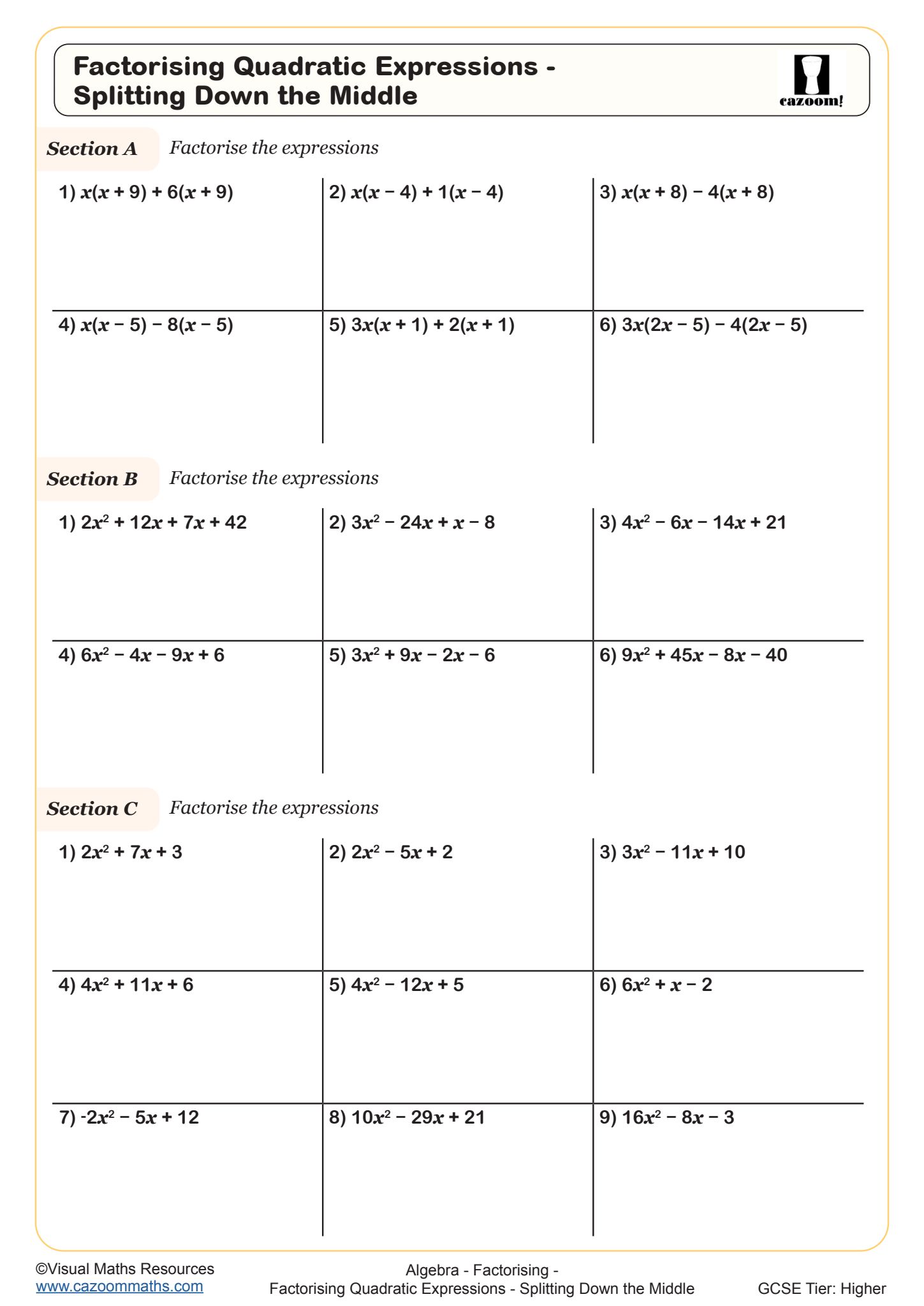
Factorising Quadratic Expressions - Splitting Down the Middle

Factorising Quadratic Expressions - Using the Area Model (A)

Factorising Quadratic Expressions - Using the Area Model (B)

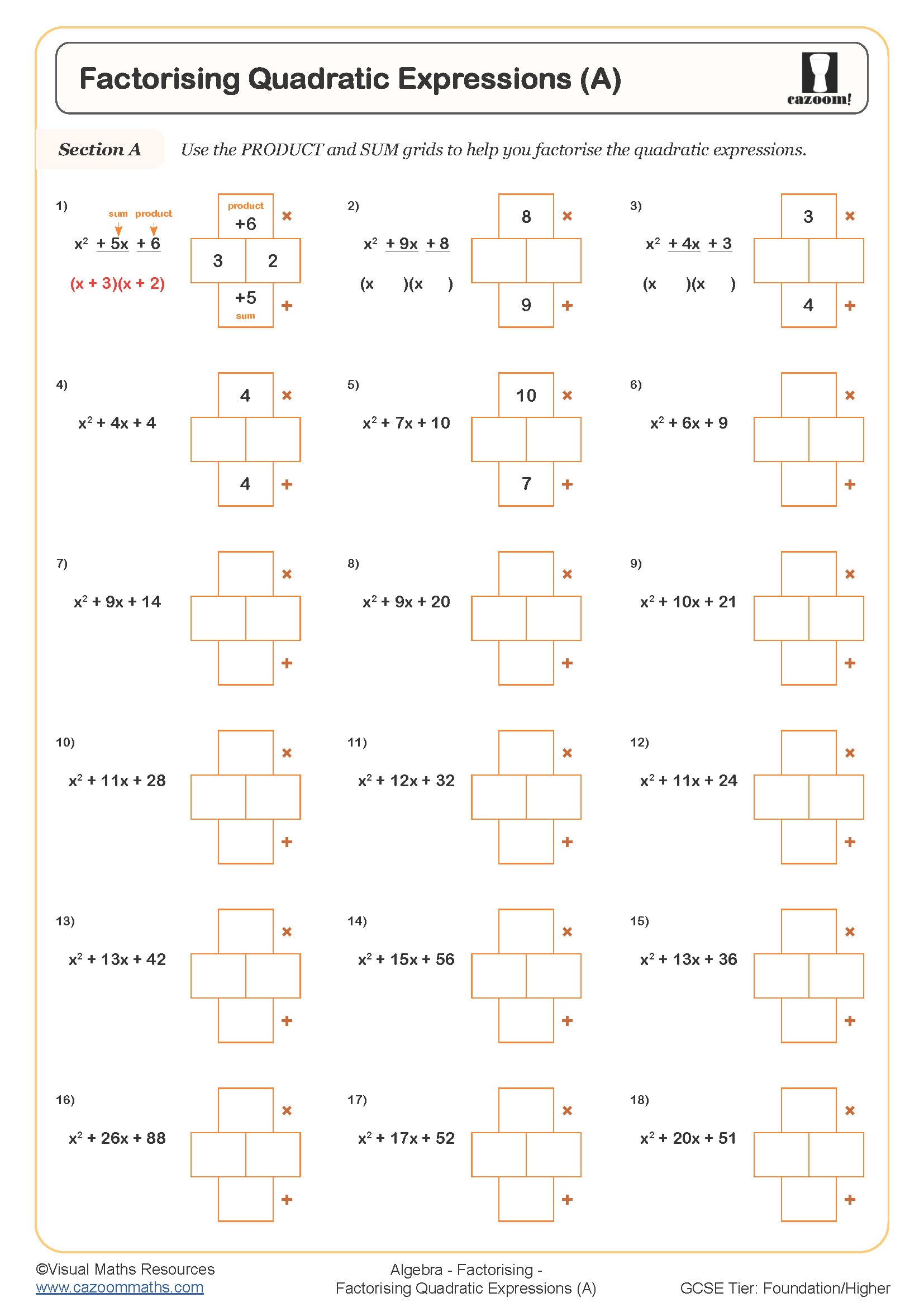
Factorising Quadratic Expressions (A)

Factorising Quadratic Expressions (B)

Factorising Quadratic Expressions (C)

Introducing Factorisation

What are the main methods for factorising quadratics?

Students at KS4 need to master three core approaches: extracting common factors first, factorising quadratics where the coefficient of x² is 1, and factorising quadratics with coefficients greater than 1. The splitting down method (also called decomposition) works systematically for all quadratic forms by finding two numbers that multiply to give ac and add to give b, then splitting the middle term before factorising in pairs.

Exam mark schemes expect students to show their method clearly, yet many lose marks by attempting mental factorising without recording their thinking. A typical error occurs with expressions like 2x² + 7x + 3, where students correctly identify the factors (2x + 1)(x + 3) but fail to check their answer by expanding. Teachers notice that students who habitually verify their factorising by multiplying out make significantly fewer sign errors and gain confidence with harder questions.

Which year groups study factorising?

These worksheets support Year 10 and Year 11 students working through the KS4 algebra curriculum. Factorising appears in the National Curriculum under 'manipulate algebraic expressions' and forms a gateway skill for solving quadratic equations, simplifying algebraic fractions, and sketching graphs. Both foundation and higher-tier GCSE papers test factorising, though the complexity differs considerably between tiers.

The progression across KS4 moves from straightforward single brackets with numerical common factors in Year 10 towards quadratics with larger coefficients, expressions requiring difference of two squares, and four-term expressions by Year 11. Higher-tier students encounter factorising as preparation for completing the square and working with more complex rational expressions. Students preparing for their mocks or final exams benefit from mixed practice that requires them to identify which technique each question demands, rather than applying one method repeatedly.

How does the difference of two squares work?

The difference of two squares is a special factorising pattern where x² - a² always factorises to (x + a)(x - a). Students must recognise when an expression fits this form: it needs exactly two terms, both perfect squares, separated by subtraction. Expressions like 9x² - 16 factorises to (3x + 4)(3x - 4), while 4x² - 25y² becomes (2x + 5y)(2x - 5y). This pattern only works with subtraction; students commonly attempt to apply it to x² + a², which doesn't factorise using real numbers.

This technique connects directly to engineering and physics contexts where students analyse wave interference patterns and signal processing. The difference of two squares appears in simplifying expressions for resonance frequencies and calculating constructive versus destructive interference. In structural engineering, the pattern emerges when calculating stress differences across materials with different thermal expansion coefficients, making this seemingly abstract algebraic skill surprisingly practical in STEM applications.

How can teachers use these factorising worksheets effectively?

The worksheets build systematic practice through carefully sequenced questions that start with clear examples before introducing variation. Each sheet focuses on specific techniques before the mixed exercises combine multiple methods, helping students develop the discrimination skills needed to identify which approach each expression requires. The included answer sheets show fully worked solutions, not just final answers, which supports students who need to identify exactly where their method breaks down.

Many teachers use these worksheets for targeted intervention with students who understand the concept but lack fluency, as timed practice helps build the speed needed for exam conditions. They work well for homework following initial teaching, as independent tasks during revision lessons, or as starter activities to maintain skills throughout Year 11. Paired work where students complete alternate questions then check each other's answers using the answer sheets encourages mathematical discussion about method choice and helps students articulate their reasoning when one approach proves more efficient than another.