KS4 Transformations Worksheets

These KS4 transformations worksheets provide targeted practice for Year 10 and Year 11 students working through rotation, reflection, translation, and enlargement on coordinate grids. Transformations form a significant portion of GCSE foundation and higher tier papers, yet teachers frequently notice that students confuse vector notation for translation with coordinates, or apply scale factors incorrectly when the centre of enlargement isn't the origin. The collection covers essential skills including describing transformations fully, performing single and combined transformations, and understanding similarity through enlargement. All worksheets are available as PDF downloads with complete answer sheets, making them suitable for independent revision, homework tasks, or assessment preparation across both foundation and higher tiers.

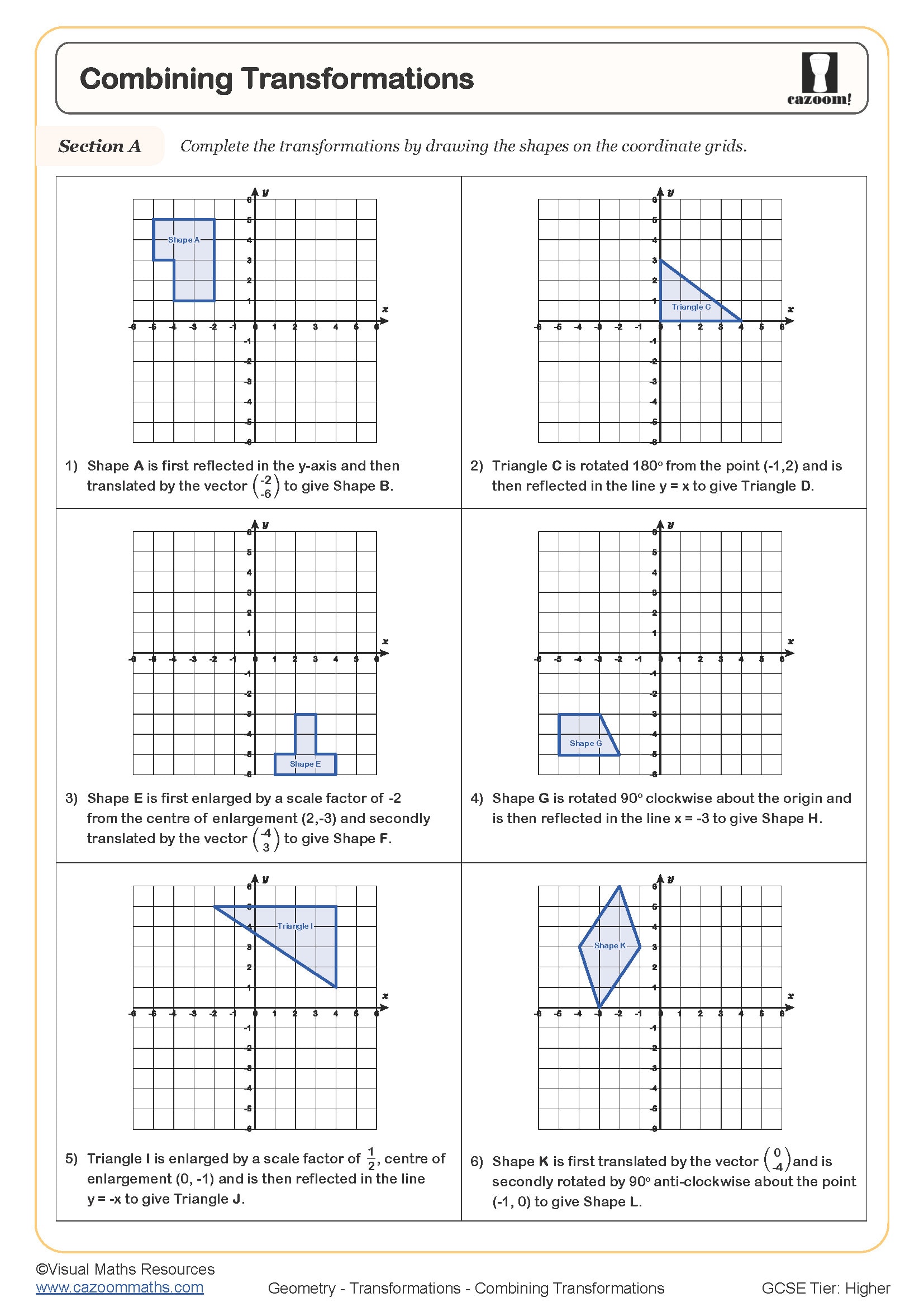
Combining Transformations

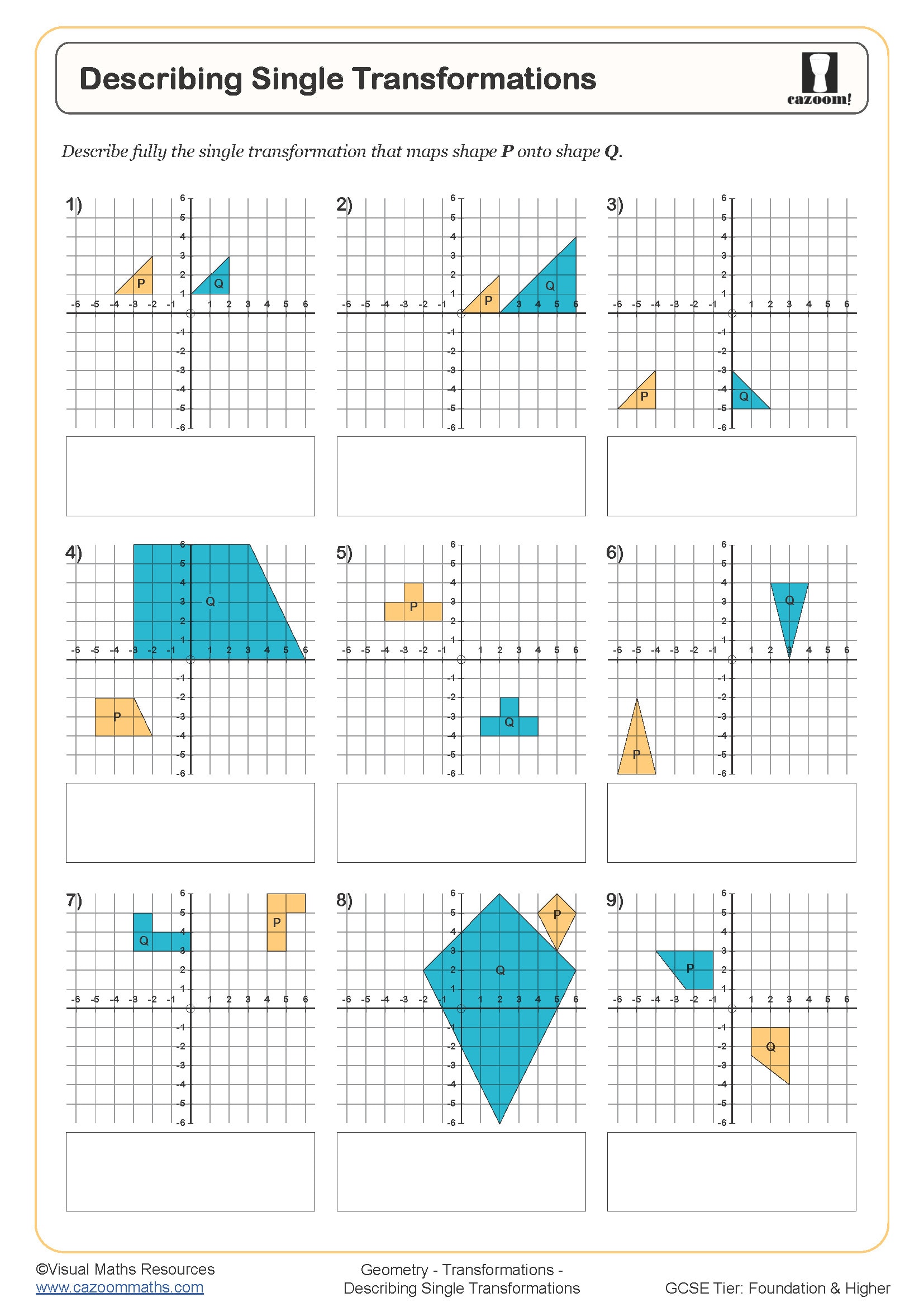
Describing Single Transformations

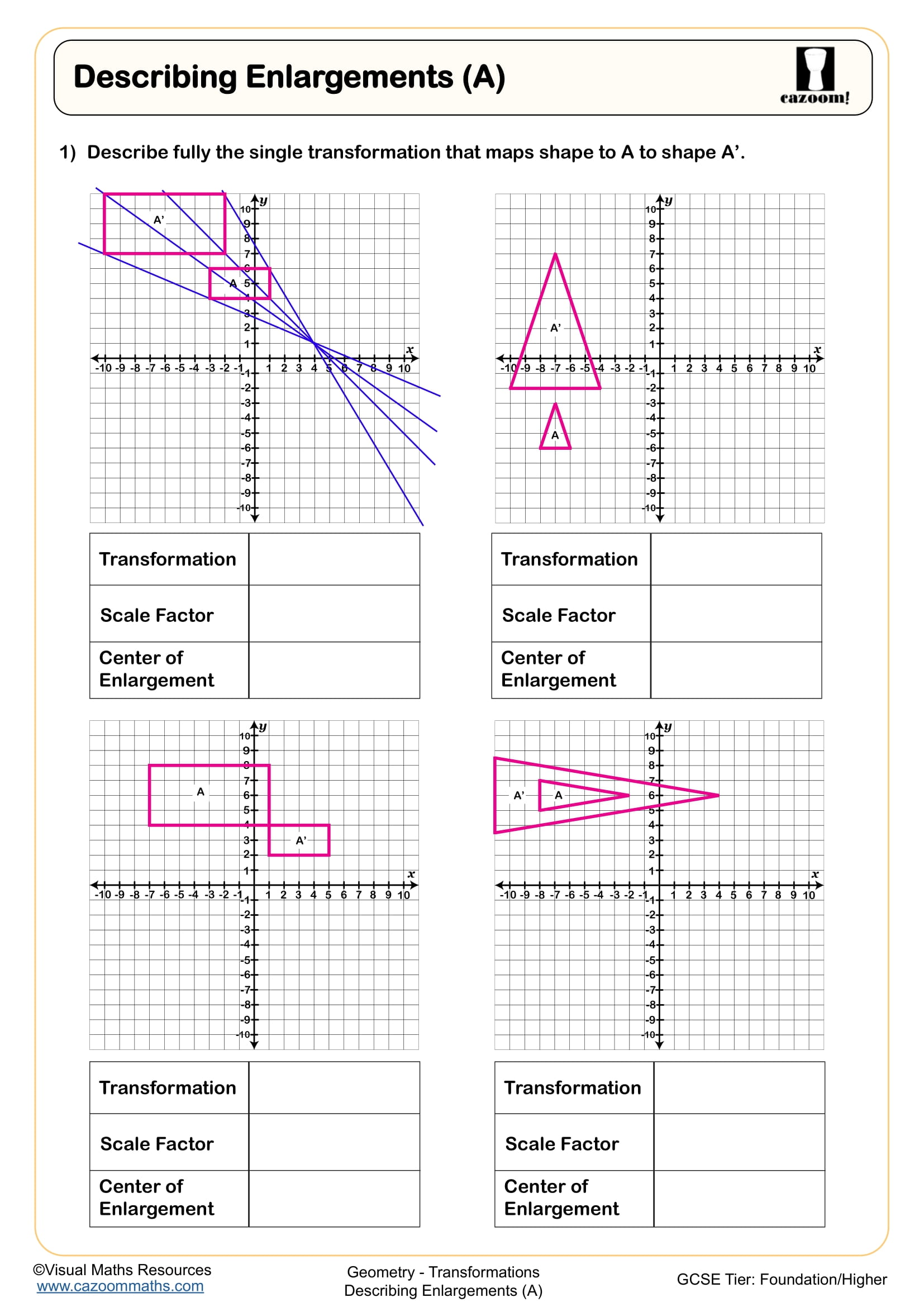
Describing Enlargements (A)

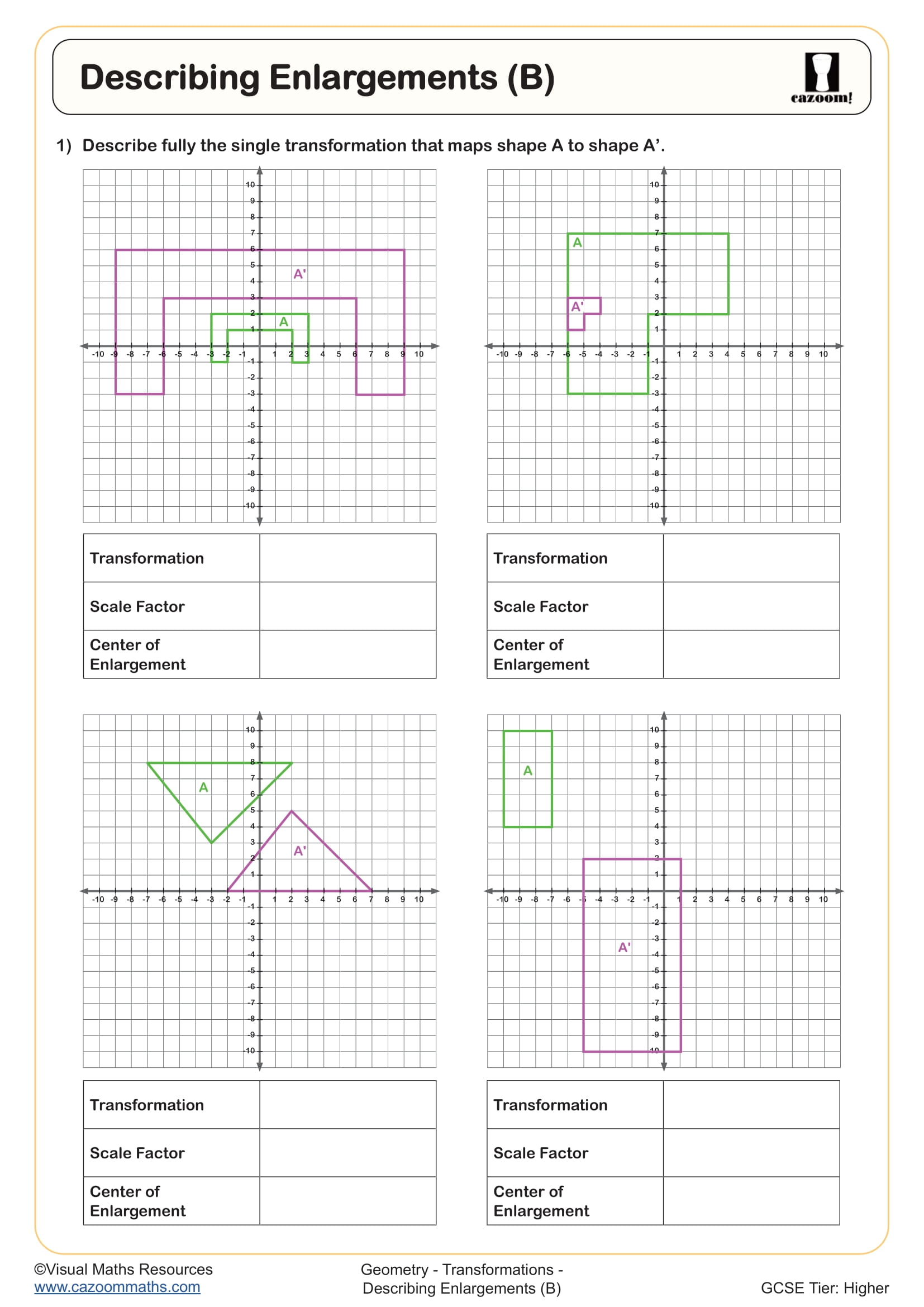
Describing Enlargements (B)

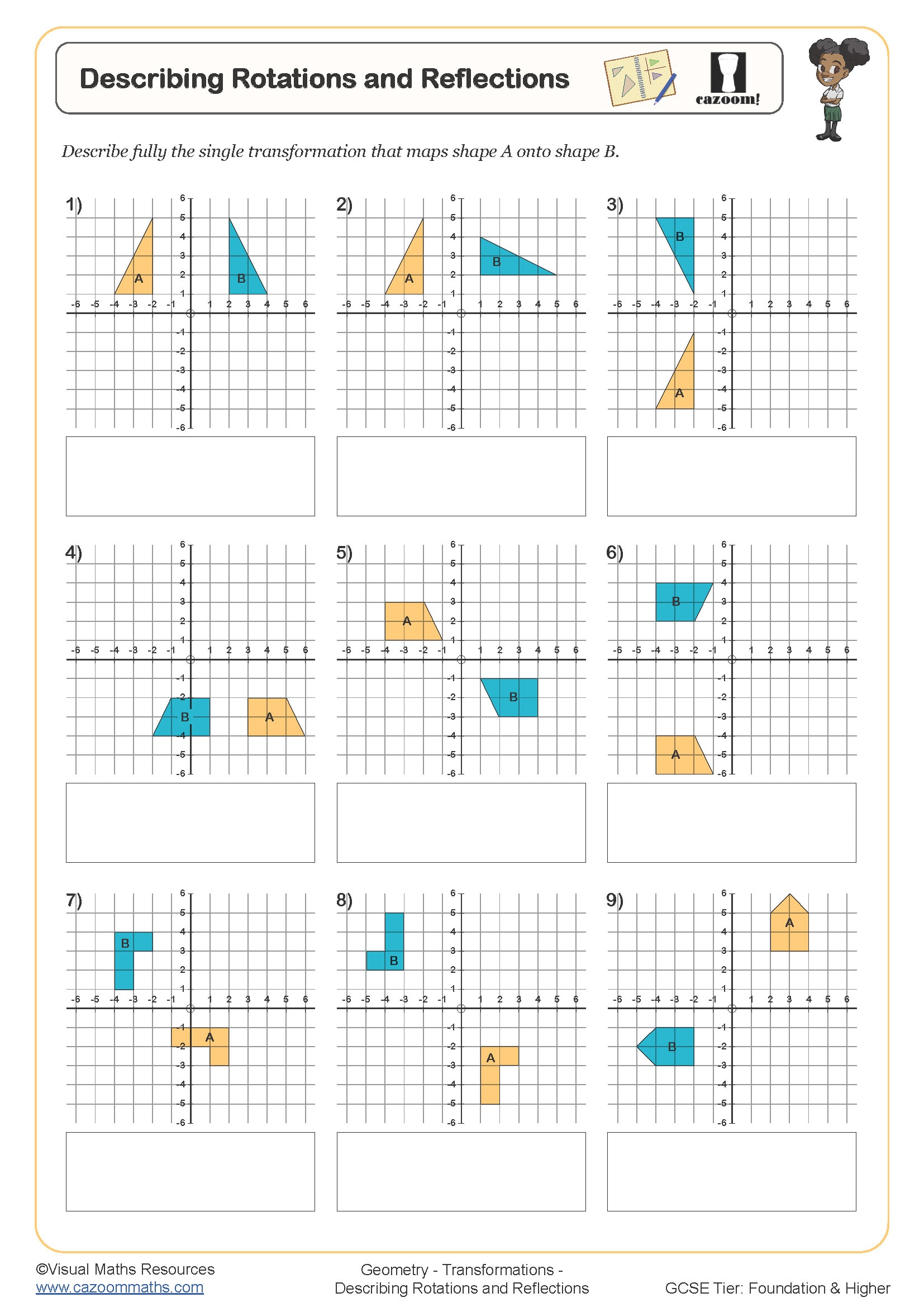
Describing Rotations and Reflections

Enlargement (C)

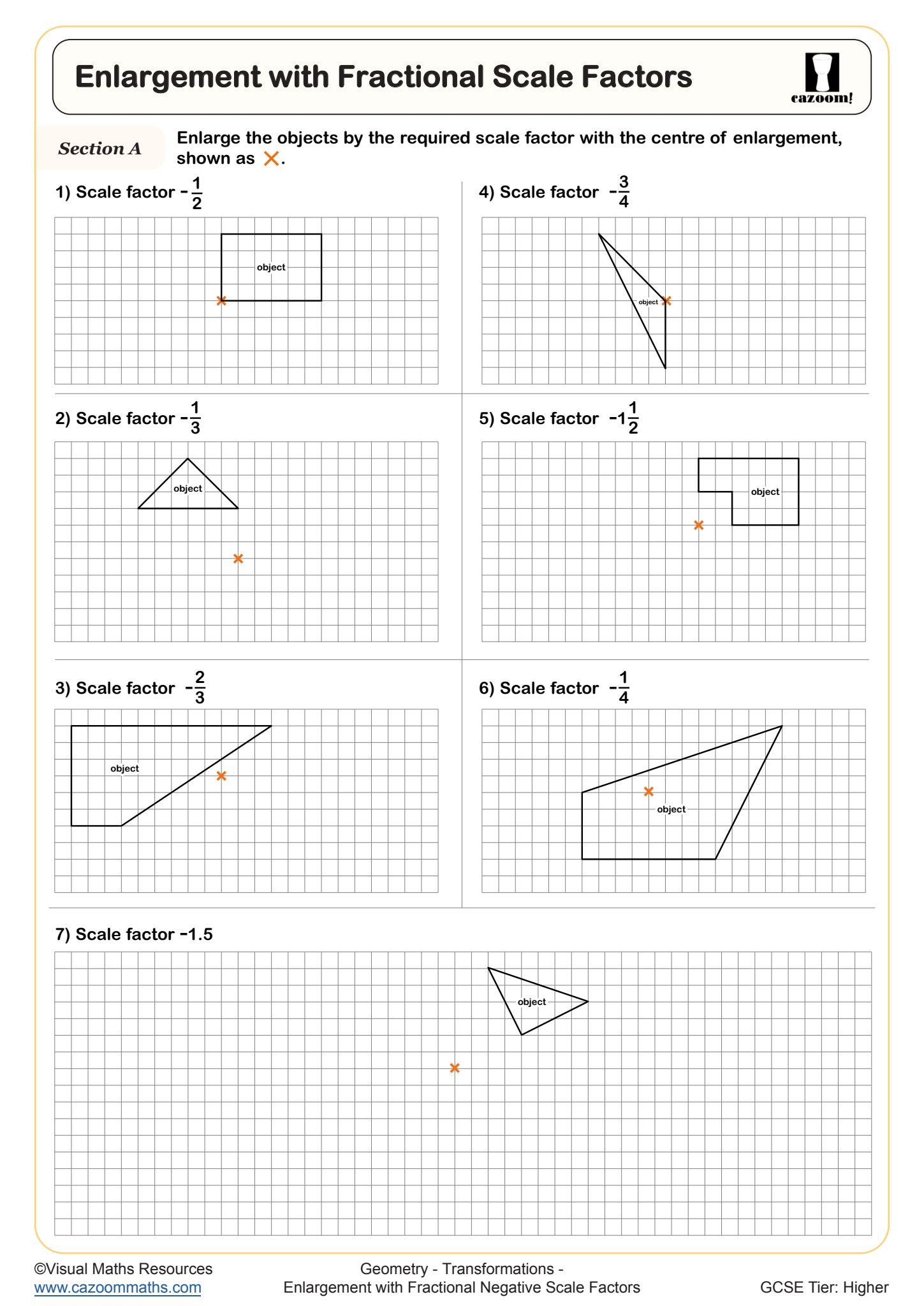
Enlargement with Fractional Negative Scale Factors

Enlargement with Fractional Scale Factors (A)

Enlargement with Fractional Scale Factors (B)

Enlargement with Negative Scale Factors

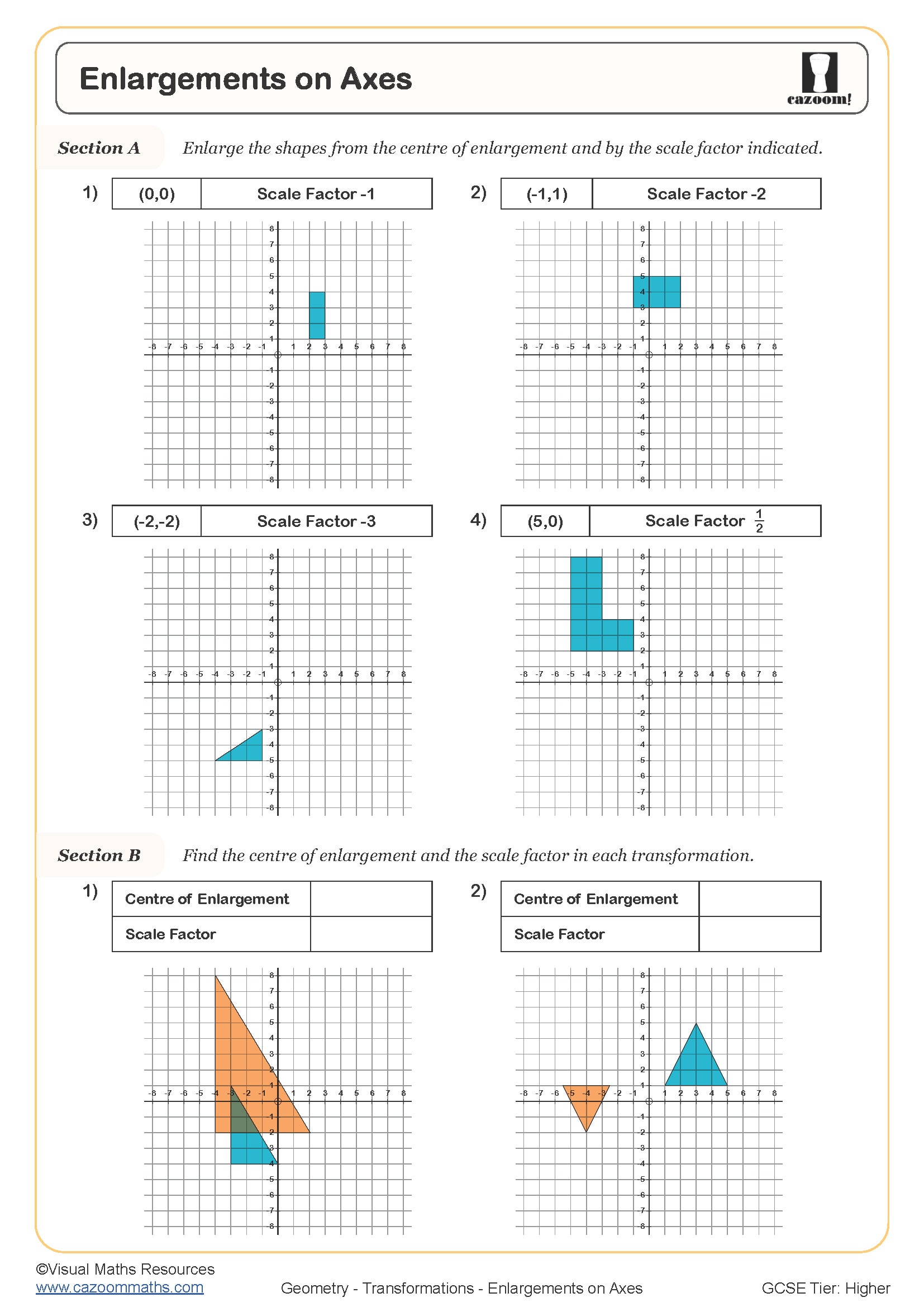
Enlargements on Axes

Enlargements Using Column Vectors

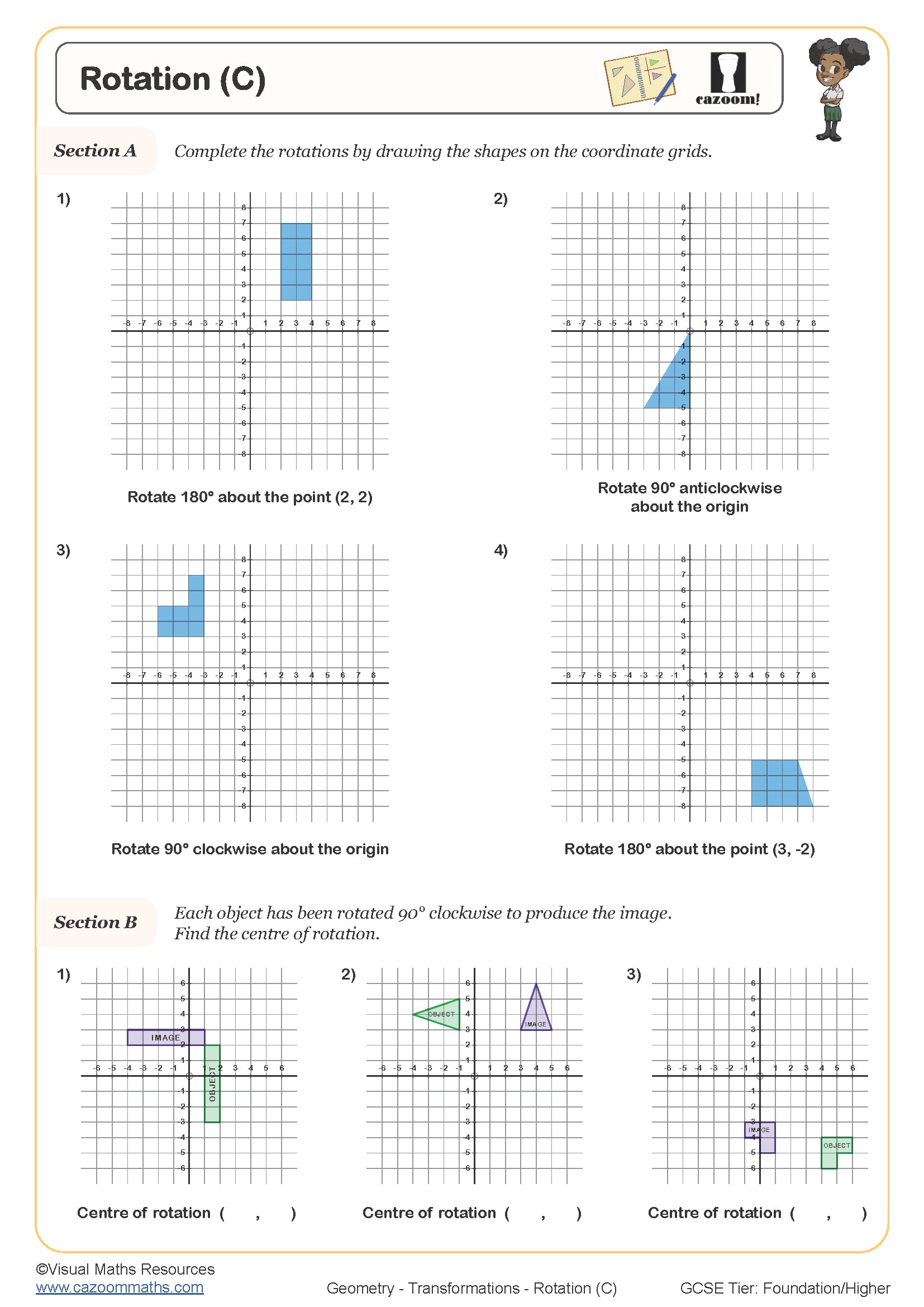
Rotation (C)

Scale Factors and Centres of Enlargement (A)

Scale Factors and Centres of Enlargement (B)

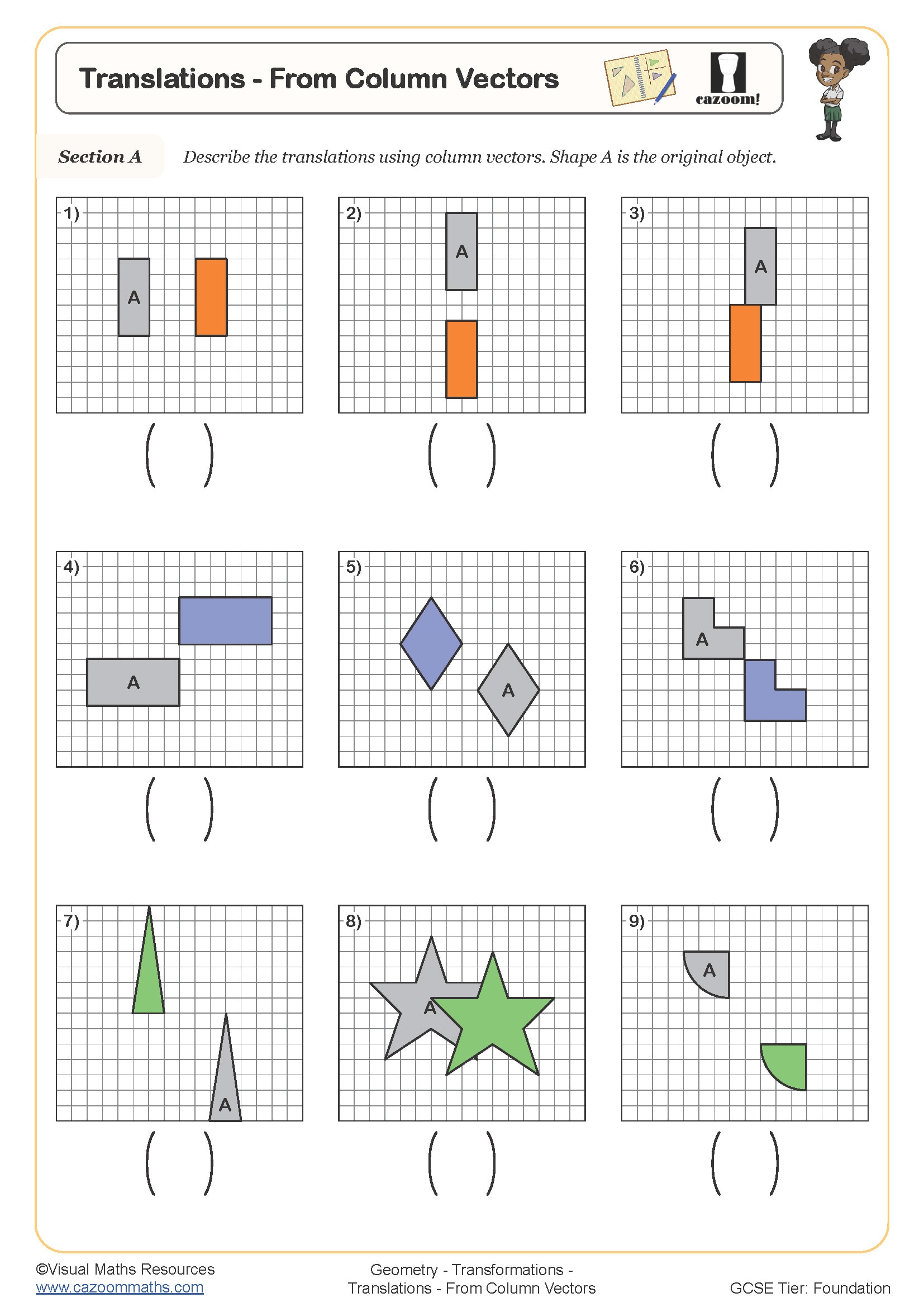
Translations - from Column Vectors

What are the four types of transformations in maths?

The four transformations students encounter at GCSE are translation (sliding a shape using a vector), reflection (flipping a shape in a mirror line), rotation (turning a shape around a fixed point), and enlargement (scaling a shape from a centre of enlargement using a scale factor). Each transformation has specific properties that must be described fully in exam questions to earn all available marks.

Teachers often notice that students lose marks by providing incomplete descriptions. For reflection, stating just "reflected in the y-axis" is sufficient, but for rotation, exam mark schemes require three pieces of information: the angle, direction (clockwise or anticlockwise), and centre of rotation. Similarly, enlargement requires both the scale factor and the coordinates of the centre of enlargement, particularly when the centre isn't positioned at the origin.

Which year groups study transformations?

Transformations appear throughout the National Curriculum, but these KS4 worksheets focus specifically on Year 10 and Year 11 content aligned with GCSE requirements. Students at this stage build on earlier work from Key Stage 3, now applying transformations to more complex shapes, working with negative scale factors for enlargement, and combining multiple transformations in sequence.

The progression across Year 10 and Year 11 involves increasing complexity rather than entirely new transformation types. Year 10 students typically consolidate single transformations and begin combining them, whilst Year 11 work emphasises exam technique, working backwards from an image to describe the transformation, and tackling higher tier challenges such as enlargements with fractional or negative scale factors. Understanding similarity through enlargement becomes particularly important for solving problems involving area and volume scale factors.

How does similarity connect to transformations?

Similarity in mathematics means shapes have the same angles but different sizes, with corresponding lengths in the same ratio. This concept links directly to enlargement, the only transformation that changes a shape's size whilst preserving its angles. When a shape undergoes enlargement with scale factor k, all lengths multiply by k, areas multiply by k², and volumes multiply by k³ (for 3D objects).

Architects and engineers apply similarity and scale factors constantly when creating scale drawings or models. A 1:50 scale architectural drawing uses a scale factor of 1/50, meaning measurements on paper can be multiplied by 50 to find actual building dimensions. Similarly, structural engineers testing bridge designs with scale models must understand that if a model uses a scale factor of 1/10, the surface area scales by 1/100, affecting calculations for material stress and load distribution across surfaces.

How can teachers use these transformation worksheets effectively?

The worksheets provide structured practice that builds from performing transformations with clear instructions through to describing transformations from diagrams, mirroring the demand progression seen in GCSE questions. Each worksheet includes answer sheets, allowing students to self-check their work during independent revision or enabling teachers to set homework with confidence that students can identify errors in their reasoning without waiting for marking.

Many teachers find these resources valuable for targeted intervention with students who struggle to visualise transformations. Paired work proves particularly effective, with one student performing a transformation whilst their partner describes it using precise mathematical language. The worksheets also work well as low-stakes retrieval practice at the start of lessons, as transformations regularly appear in GCSE papers and students benefit from regular exposure. For higher tier students, the similarity content supports connections to other topics including trigonometry and circle theorems where recognising similar triangles becomes essential.