Year 10 Algebraic Fractions Worksheets
What skills do grade 10 fractions worksheets cover?
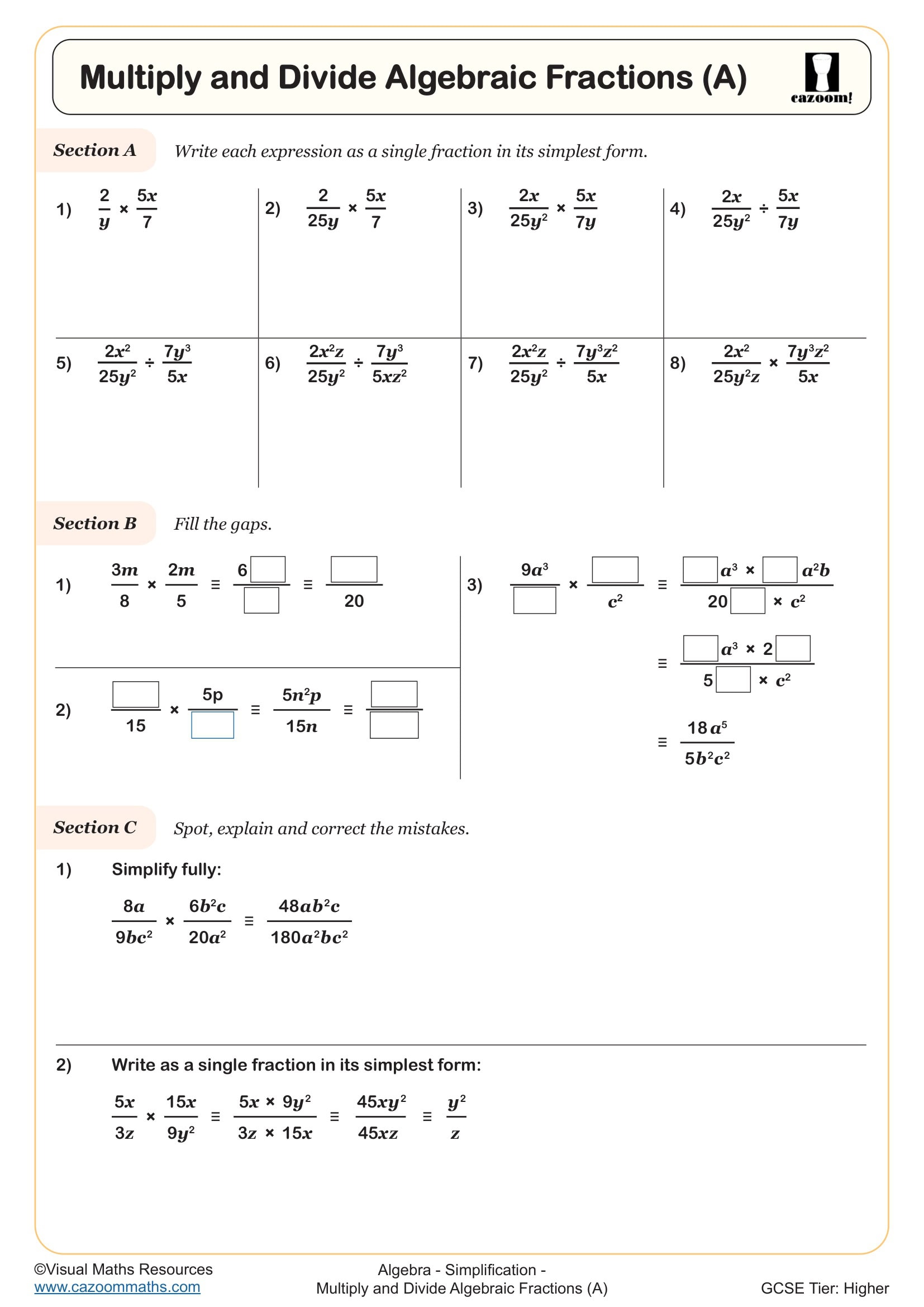
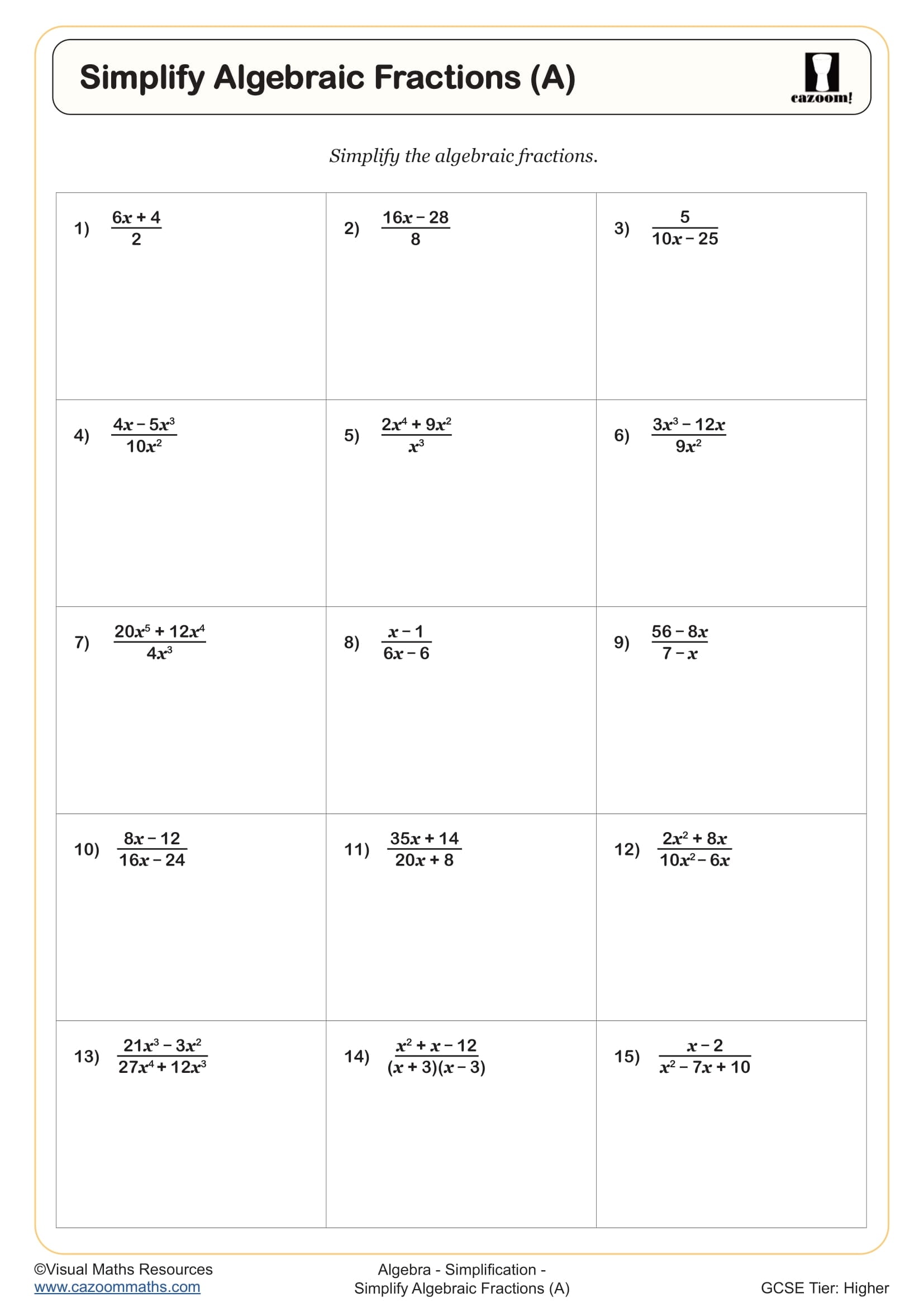
Grade 10 fractions worksheets at KS4 focus on algebraic fractions rather than numeric fractions, which students encountered in earlier key stages. These worksheets develop skills in simplifying, adding, subtracting, multiplying, and dividing expressions where variables appear in numerators, denominators, or both. Students learn to factorise quadratics and linear expressions before cancelling common factors, apply arithmetic rules to algebraic contexts, and work with rational expressions confidently.
A typical error occurs when students attempt to cancel terms across addition or subtraction rather than multiplication. For example, in (x + 3)/(x + 5), students might incorrectly cancel the x terms. Exam mark schemes consistently penalise this mistake, which stems from not recognising that cancellation requires common factors, not just common terms. These worksheets include problems designed to address this specific misconception through careful sequencing.
Which year group studies algebraic fractions?
Algebraic fractions appear in the Year 10 curriculum as part of KS4 mathematics, typically on the Higher tier GCSE pathway. Students at this level have already mastered numeric fractions and basic algebraic manipulation, making them ready to combine these skills. The National Curriculum expects students to simplify and perform operations on algebraic fractions, recognising these as rational expressions that follow the same fundamental rules as their numeric counterparts.
Within Year 10, the difficulty progresses significantly. Early worksheets focus on straightforward division and subtraction with linear expressions, whilst later materials introduce quadratic denominators requiring factorisation before simplification. Students who struggle with factorising quadratics will find algebraic fractions particularly challenging, as these two skills must work together fluently. Many teachers schedule this topic after securing factorisation skills to avoid compounding difficulties.
How do you subtract algebraic fractions?
Subtracting algebraic fractions follows the same process as numeric fractions: find a common denominator, rewrite each fraction with this denominator, then subtract the numerators whilst keeping the denominator unchanged. The key difference lies in factorising expressions to identify the lowest common multiple of algebraic denominators. For example, when subtracting 3/(x + 2) from 5/(x − 1), the common denominator becomes (x + 2)(x − 1), requiring students to multiply each numerator by the missing factor before combining.
This skill has direct applications in physics and engineering, particularly when working with formulae involving rates or combined resistances. Electrical engineers regularly combine resistances in parallel circuits using 1/R_total = 1/R₁ + 1/R₂, which requires manipulating algebraic fractions to solve for unknown values. Understanding how to subtract and combine algebraic fractions allows students to rearrange complex formulae confidently, a skill that extends well beyond GCSE into technical fields and further mathematics.
How can these worksheets support different learners?
The worksheets scaffold learning through carefully graded questions that begin with single-operation problems before introducing multi-step manipulations. Early questions might ask students to divide algebraic fractions where cancellation is straightforward, whilst later problems require factorising both numerators and denominators before simplifying. This structure allows students to build confidence with fundamental techniques before tackling the compound skills that appear in exam questions. Worked examples and answer sheets enable students to self-check and identify where their method breaks down.
Teachers use these resources flexibly depending on class needs. In mixed-ability settings, the worksheets work well for differentiated homework, with stronger students attempting later questions whilst others consolidate basic division and subtraction. They're particularly effective for intervention sessions, where small groups can work through problems together, discussing each step aloud to identify misconceptions. Some teachers use individual worksheets as starter activities to assess whether students have retained factorisation skills before introducing new algebraic fraction operations.