Year 10 Area and Perimeter Worksheets
Area of a Triangle Using Pythagoras' Theorem

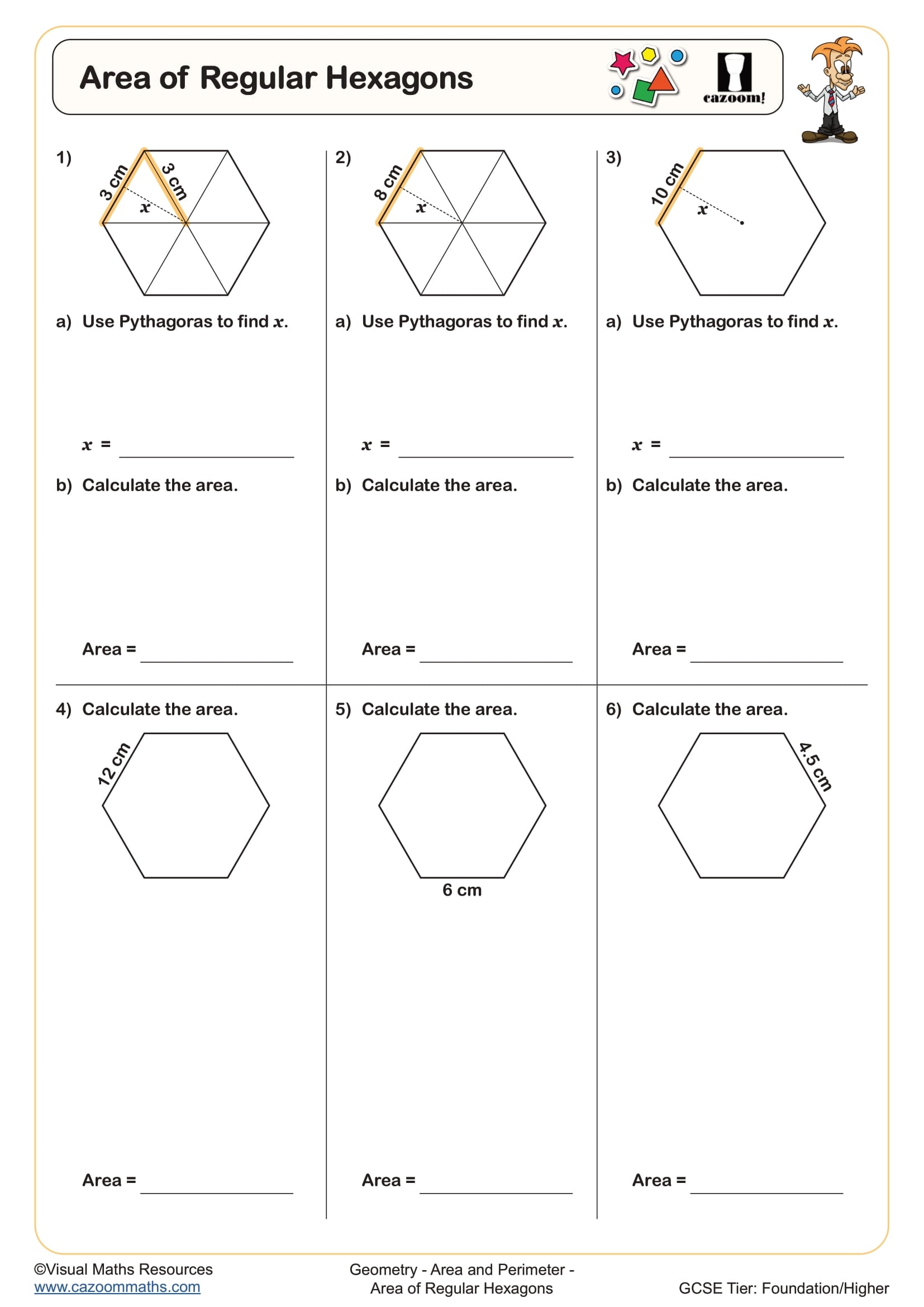
Area of Regular Hexagons
Area of Sectors and Arc Lengths

Area of Sectors and Segments
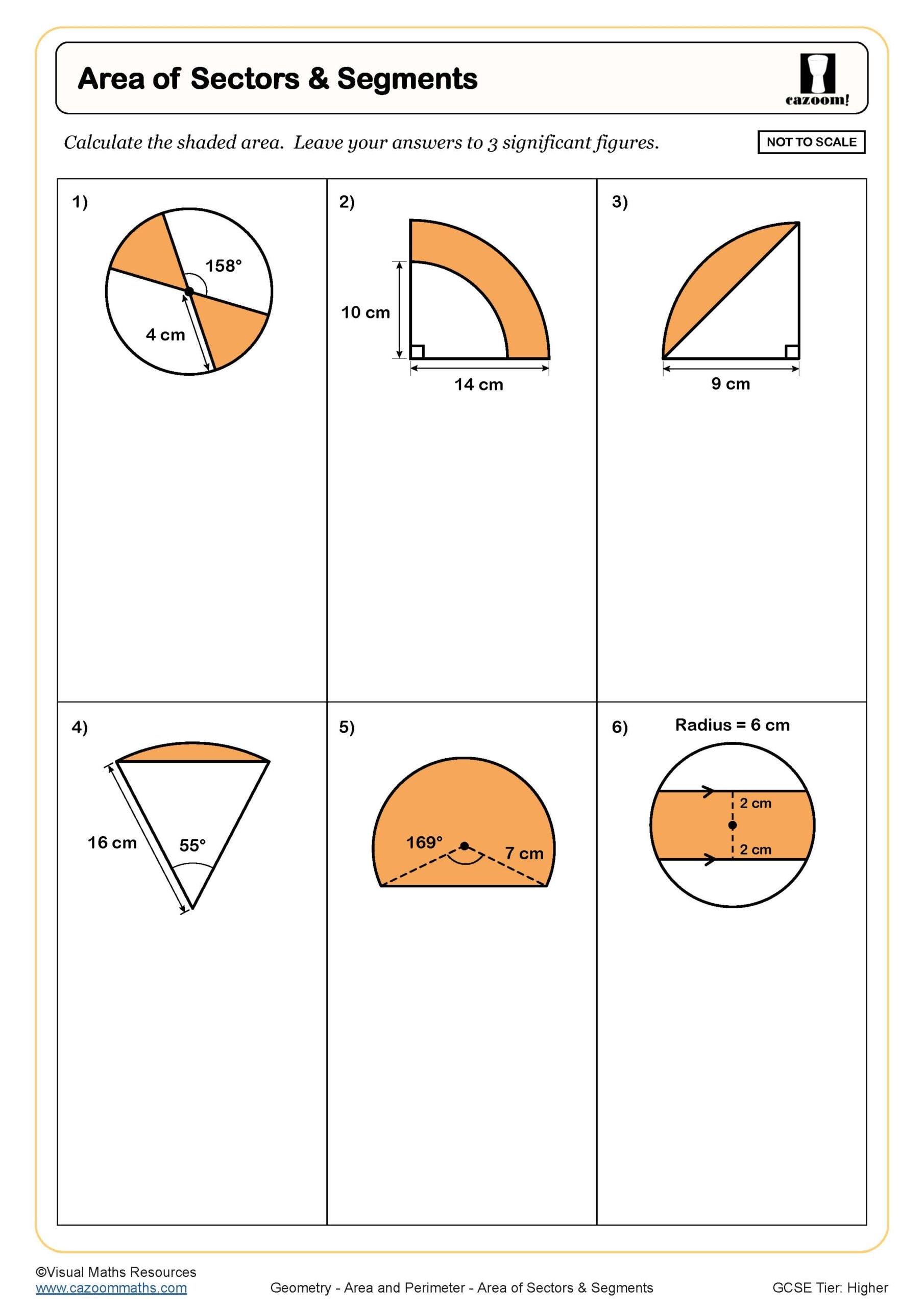
Area of Sectors and Segments (With Clues)
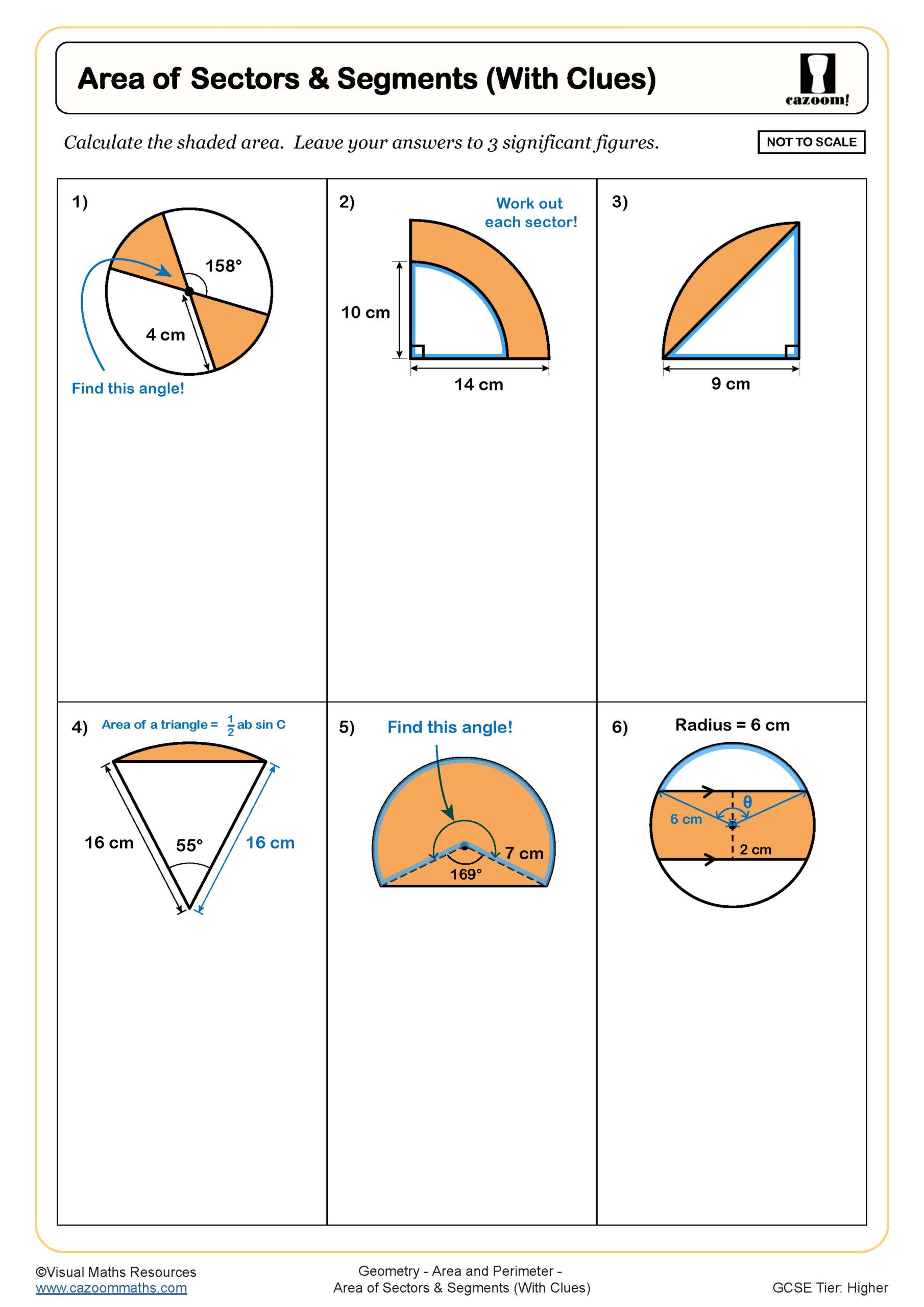
Area of Triangles (With Clues)
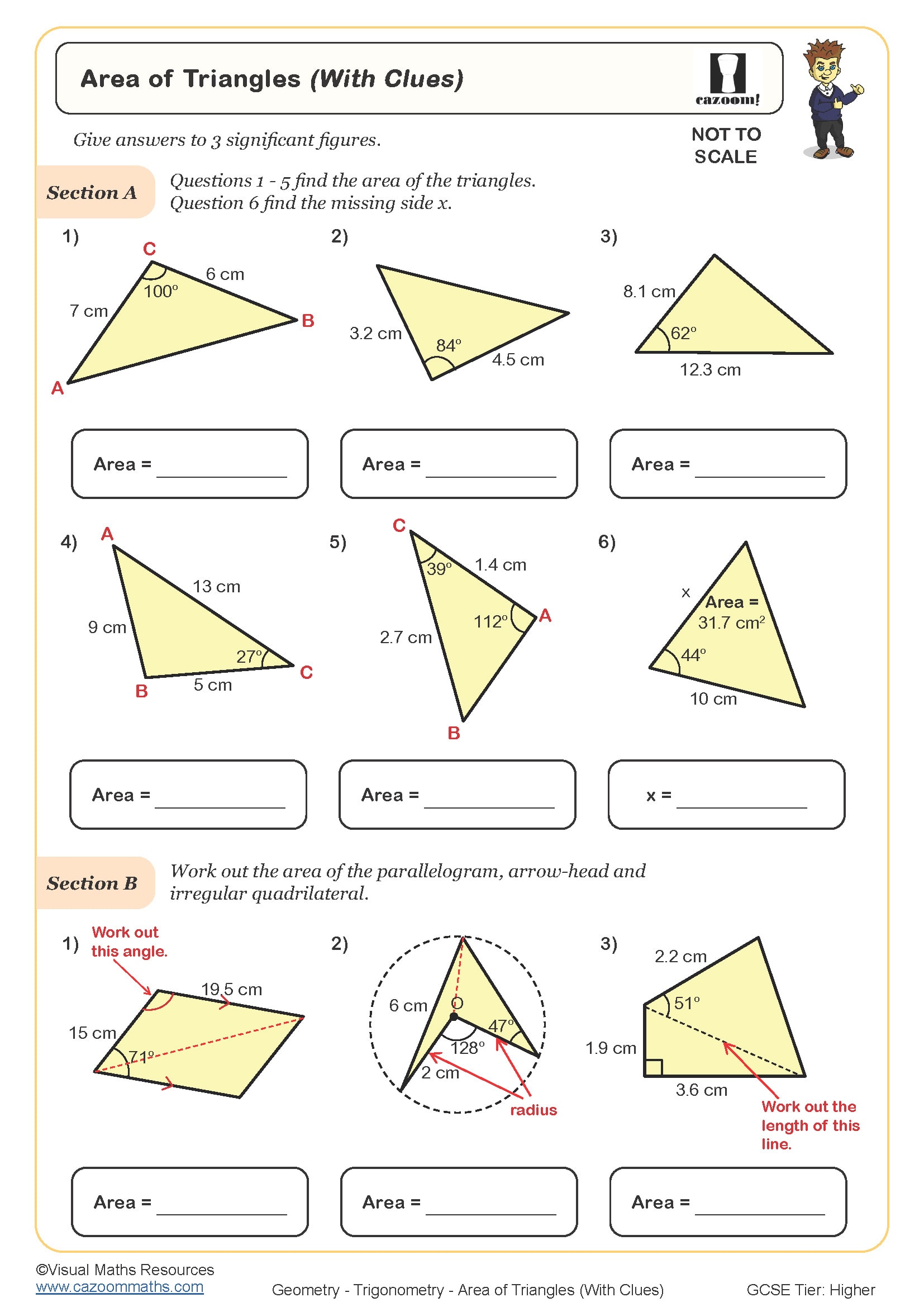
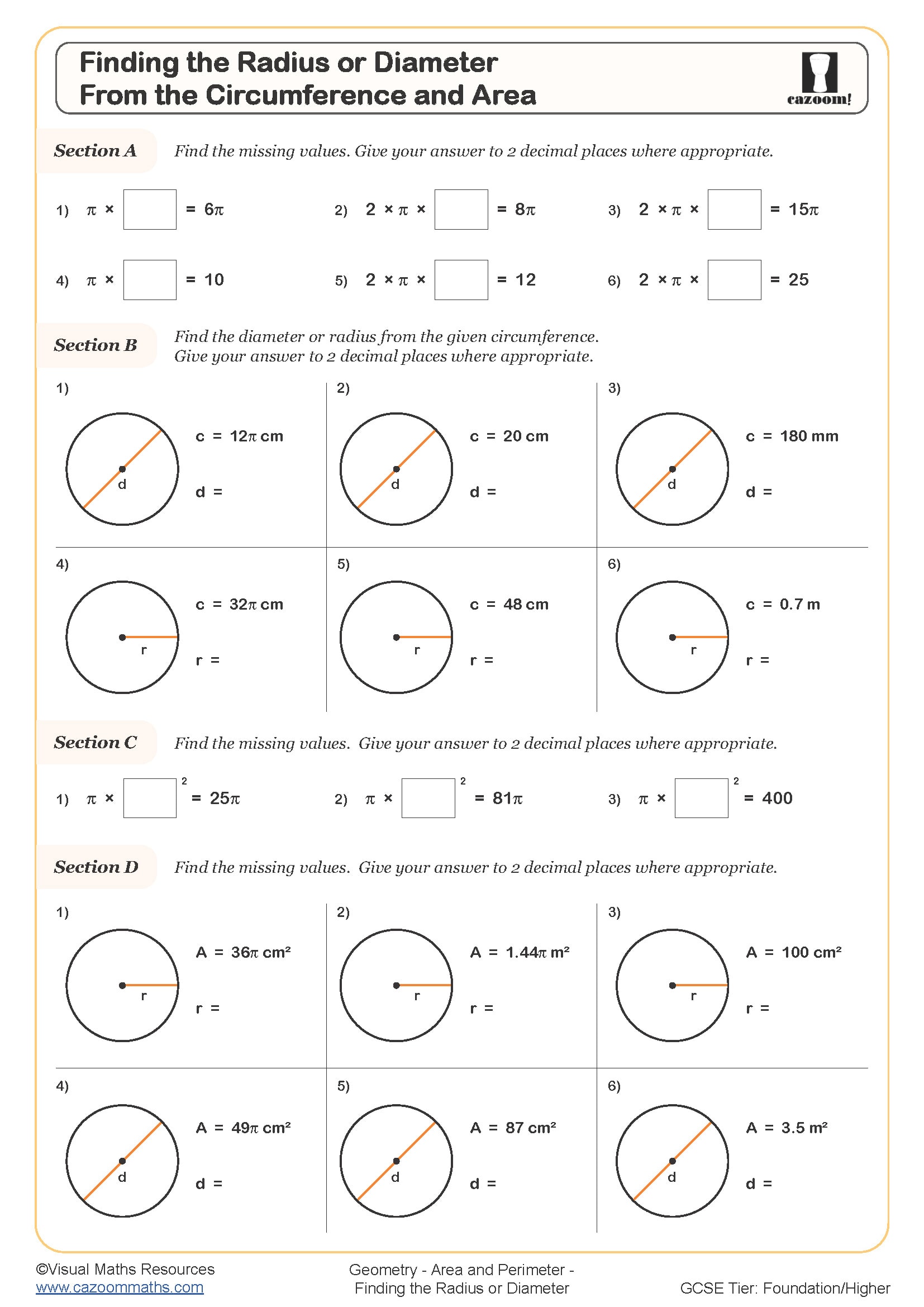
Finding the Radius or Diameter from the Circumference and Area
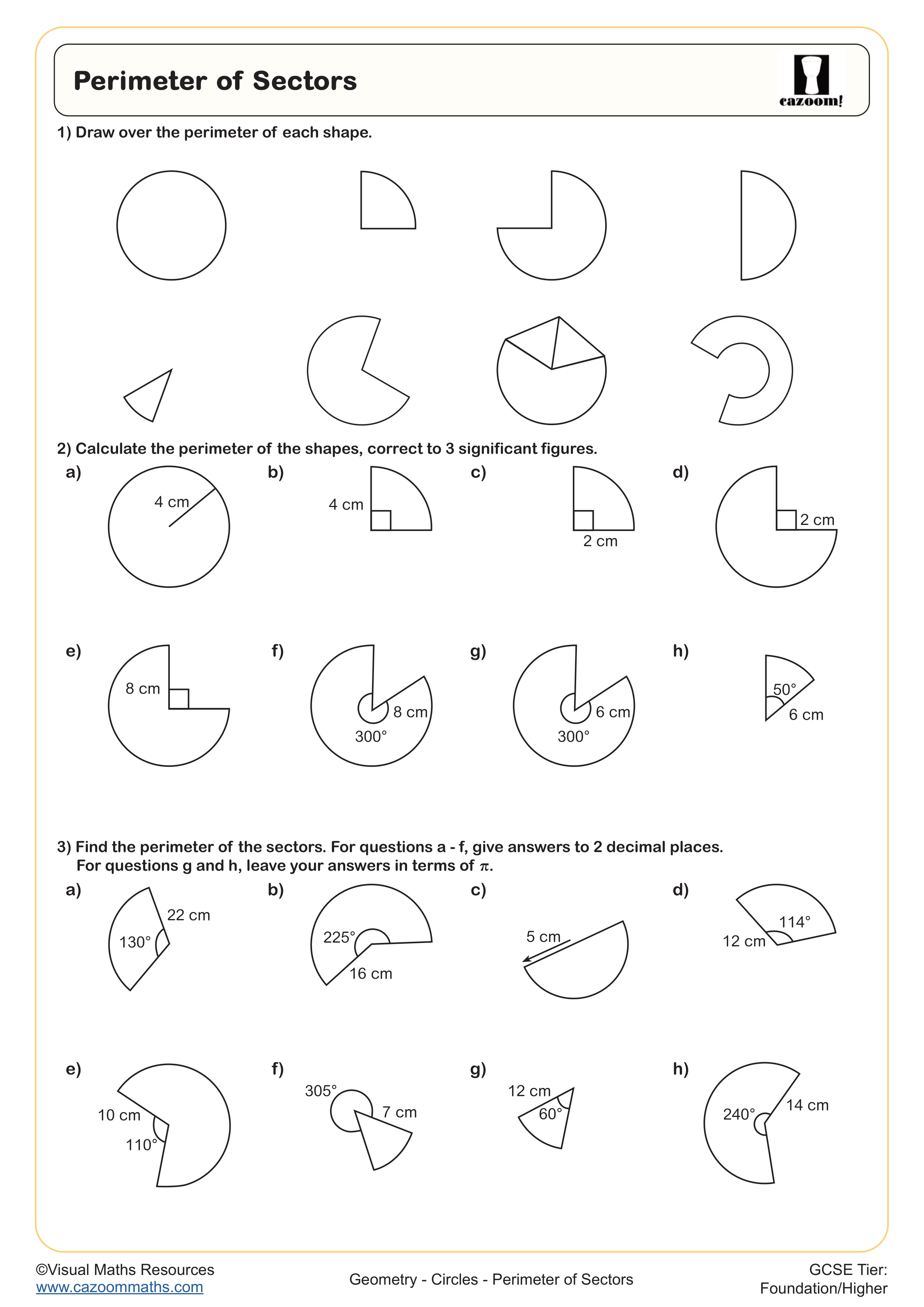
Perimeter of Sectors
Perimeter Using Pythagoras' Theorem

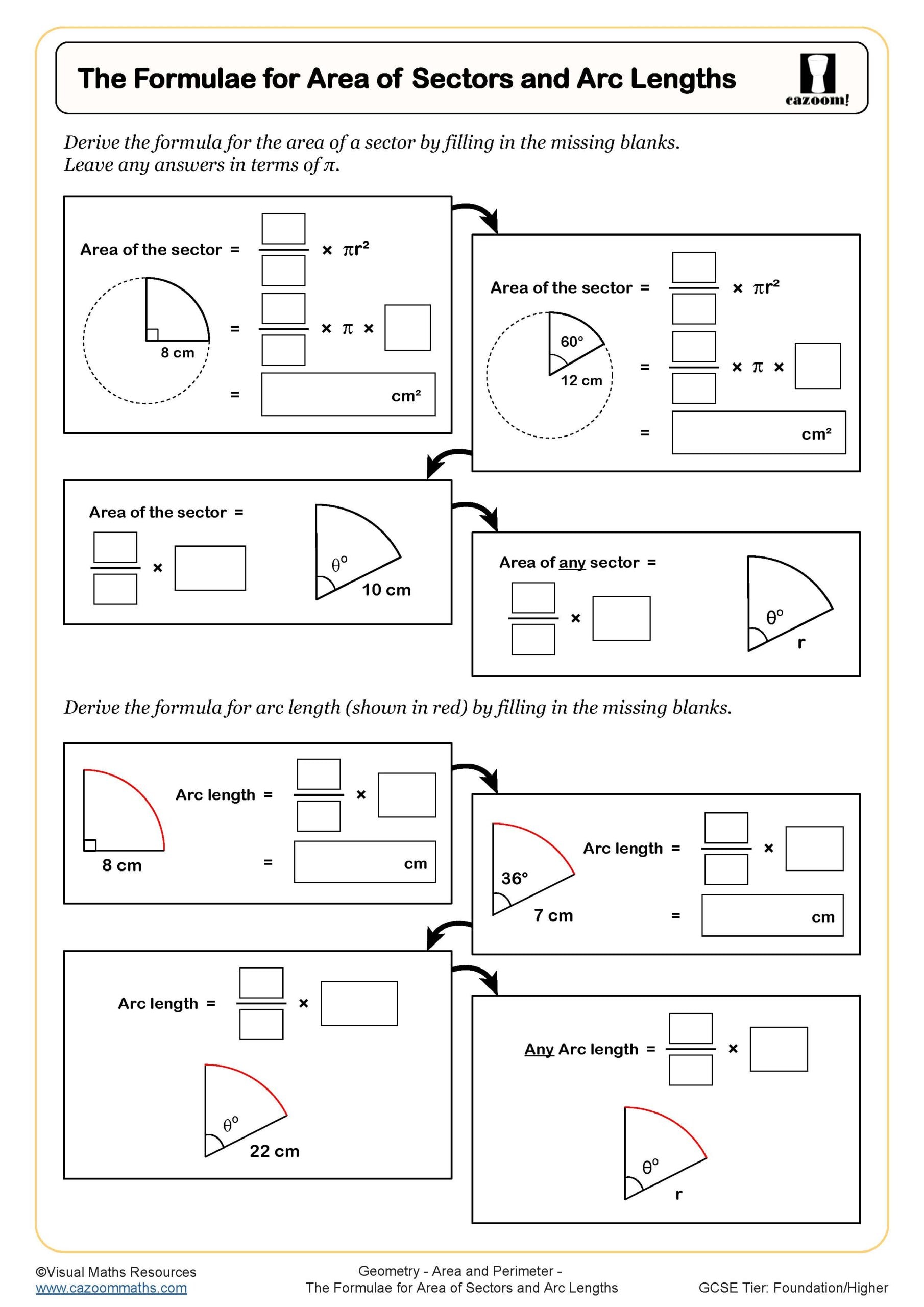
The Formulae for Area of Sectors and Arc Lengths
What area and perimeter topics do Year 10 students need to master?
Year 10 students build on their Key Stage 3 foundation by applying area and perimeter to more complex scenarios. They work with compound shapes that combine rectangles, triangles and trapeziums, calculate the circumference and area of circles using π, and solve problems involving sectors and segments. The curriculum also expects students to rearrange formulae to find missing dimensions when given an area or perimeter, a skill that links directly to algebra.
Students lose marks in exams when they fail to show the perimeter calculation for composite shapes clearly, missing out on method marks even when their final answer is incorrect due to an arithmetic slip. Teachers also notice that many students round π too early in circle calculations rather than keeping it in exact form until the final answer, leading to accuracy errors that cost marks on higher tier papers.
Which year groups study area and perimeter at KS4?
Area and perimeter worksheets at KS4 are primarily designed for Year 10 students as part of their GCSE preparation, though Year 11 students often revisit these topics during revision. This builds directly on the Key Stage 3 curriculum where students learned basic formulae for standard shapes, moving now towards problem-solving applications and working with more complex composite shapes and circles.
The progression in Year 10 involves increased algebraic manipulation alongside geometric reasoning. Early worksheets might focus on calculating areas when all dimensions are given, whilst later exercises require students to form and solve equations when only the perimeter or area is known. Higher tier students also encounter arc lengths and sector areas, which combine circle geometry with fractional reasoning and require precise use of formula.
How is perimeter used in real-world contexts?
Perimeter calculations appear throughout construction, landscaping and manufacturing contexts where materials must be ordered or costs estimated based on boundary measurements. Students might calculate fencing required for irregular plots, edging needed for garden designs, or the amount of trim needed for composite shapes in joinery. Understanding perimeter also underpins more advanced work in architecture and engineering where surface boundaries determine material quantities.
In STEM careers, perimeter concepts extend into fields like civil engineering where professionals calculate road lengths around developments, or in manufacturing where packaging designers must minimise perimeter to reduce material waste whilst maintaining specific areas. Environmental scientists also use perimeter-to-area ratios when studying habitat fragmentation, demonstrating how this Year 10 skill connects to ecological research and conservation planning that students may encounter in geography or biology.
How can teachers use these worksheets effectively in lessons?
The worksheets provide structured practice that moves from standard calculations through to problem-solving questions requiring multiple steps. Teachers can use earlier questions as guided examples on the board, demonstrating how to annotate diagrams with calculated missing lengths before attempting the final perimeter or area. The variety of question styles allows differentiation within mixed-ability groups, with some students completing foundational exercises whilst others tackle algebraic problems.
Many teachers set these worksheets for homework after introducing a new concept, then use the answer sheets during the following lesson for peer marking and class discussion of common errors. They work particularly well for intervention sessions where small groups can talk through their methods, or as retrieval practice before mock exams. The downloadable format means students can annotate diagrams directly, showing their working in the way that GCSE mark schemes reward, rather than attempting calculations mentally and losing valuable method marks.