Menu

PRIMARYSECONDARYGCSE REVISION
SCHOOLSSEARCH
LOGINFREE TRIAL

Year 10 Area Model Worksheets

These Year 10 area model worksheets help students develop a visual approach to algebraic multiplication, particularly when expanding brackets and multiplying binomials. The area model provides a spatial representation that supports understanding of distributive properties and polynomial multiplication at KS4 level. Teachers frequently notice that students who struggle with traditional FOIL methods or abstract algebraic manipulation gain confidence when they can see how terms combine geometrically. The area model worksheets bridge the gap between concrete mathematical thinking and abstract algebraic processes, building foundations for quadratic expansion and factorisation. All worksheets download as PDFs with complete answer sheets, allowing students to check their working independently and teachers to mark efficiently.

Completing the Square - Using Algebra Tiles

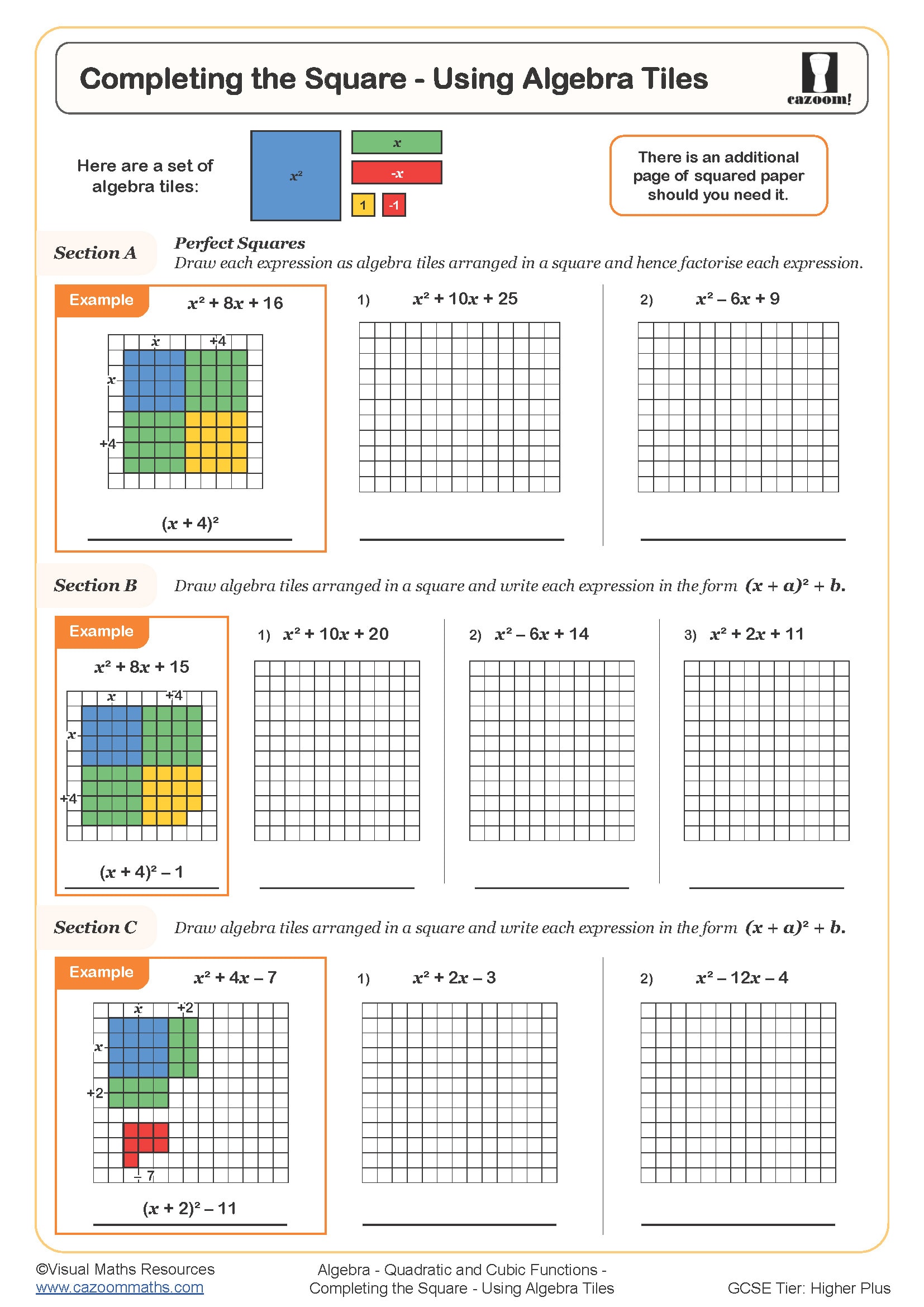
Completing the Square - Using Algebra Tiles Worksheet created for students in KS4

Expanding Double Brackets (A) Using the Grid Method

Expanding Double Brackets Worksheet fit for students in year 8, 9 and year 10

Expanding Double Brackets with Surds - Using the Grid Method

Expanding Double Brackets with Surds - Using the Grid Method worksheet

Expanding Triple Brackets (A)

Expanding Triple Brackets Worksheet created for students in KS4

Factorising Quadratic Expressions - Using the Area Model (A)

Factorising Quadratic Expressions - Using the Area Model (A) worksheet

Factorising Quadratic Expressions - Using the Area Model (B)

Factorising Quadratic Expressions - Using the Area Model (B) worksheet

All worksheets are created by the team of experienced teachers at Cazoom Maths.

What is the area model in maths?

The area model is a visual strategy that represents multiplication as the area of a rectangle, where each dimension corresponds to one of the factors being multiplied. In Year 10 algebra, this typically involves drawing a rectangle divided into sections, with algebraic expressions labelling the sides and each section showing the product of the corresponding terms. The total area, found by summing all sections, gives the expanded form of the expression.

Students often misunderstand how to position terms correctly in the grid, particularly when dealing with subtraction or negative coefficients. Teachers notice that pupils sometimes forget to include the negative sign when multiplying, treating −3x as if it were 3x in the area model sections. Explicitly labelling each dimension and using colour coding for positive and negative terms helps prevent these errors during the expansion process.

Which year groups use area model worksheets?

These particular worksheets are designed for Year 10 students working within the KS4 curriculum, where the area model supports algebraic manipulation required for GCSE Higher Tier mathematics. At this stage, the method moves beyond simple numerical multiplication to focus on expanding products of binomials such as (x + 3)(x + 5) or expressions involving negative terms and coefficients.

Whilst younger students encounter area models with whole numbers and simple expressions in Key Stage 3, Year 10 work deepens this understanding by connecting it to quadratic expressions and more complex algebraic forms. The progression leads naturally into factorising quadratics, where students can use the area model in reverse, and prepares them for completing the square, where spatial reasoning about algebraic structure proves valuable.

How does the area model help with expanding brackets?

The area model breaks down bracket expansion into manageable visual steps, making the distributive property explicit rather than abstract. When expanding (2x + 3)(x − 4), students draw a rectangle with dimensions labelled by each binomial, then divide it into four sections corresponding to 2x × x, 2x × (−4), 3 × x, and 3 × (−4). Each section's area is calculated and recorded, before combining like terms to reach the final expanded form of 2x² − 5x − 12.

This spatial approach connects directly to calculating actual areas in design and construction contexts. Architects and engineers routinely decompose complex rectangular spaces into smaller sections when calculating materials needed or planning room layouts. Understanding how total area breaks down into component parts helps students grasp why dimensional analysis matters in STEM fields, where measurements and calculations must account for every contributing factor accurately.

How can teachers use these area model worksheets effectively?

The worksheets provide structured practice that moves from simpler products like (x + 2)(x + 5) through to more challenging expressions involving negative terms, larger coefficients, and ultimately expressions requiring multiple steps of simplification. Grids are pre-drawn on some questions whilst others require students to construct their own area models, building independence gradually. The progression allows teachers to identify precisely where students' understanding breaks down, whether in setting up the model or in the multiplication and combination stages.

Many teachers use these worksheets during intervention sessions with students who find standard algebraic methods confusing, as the visual scaffold often unlocks understanding that purely symbolic manipulation doesn't achieve. They work particularly well for homework following initial teaching, allowing students to consolidate the method at their own pace with answer sheets for immediate feedback. Paired work sessions where students explain their area model layouts to each other also strengthen procedural fluency and mathematical communication skills simultaneously.