Year 11 Area and Perimeter Worksheets

Year 11 area and perimeter worksheets provide targeted GCSE revision for students preparing for their final exams. These resources cover the full range of requirements for both Foundation and Higher tiers, from calculating perimeter of composite shapes to applying area formulas in complex problem-solving contexts. Teachers frequently notice that Year 11 students can recall individual formulas but struggle when questions require them to decide which formula to apply or when they need to work backwards from a given area to find missing dimensions. Each worksheet downloads as a PDF with complete answer sheets included, making them suitable for independent revision, homework, or intervention sessions where students need to check their own working and identify gaps in understanding before exams.

Area of a Triangle Using Pythagoras' Theorem

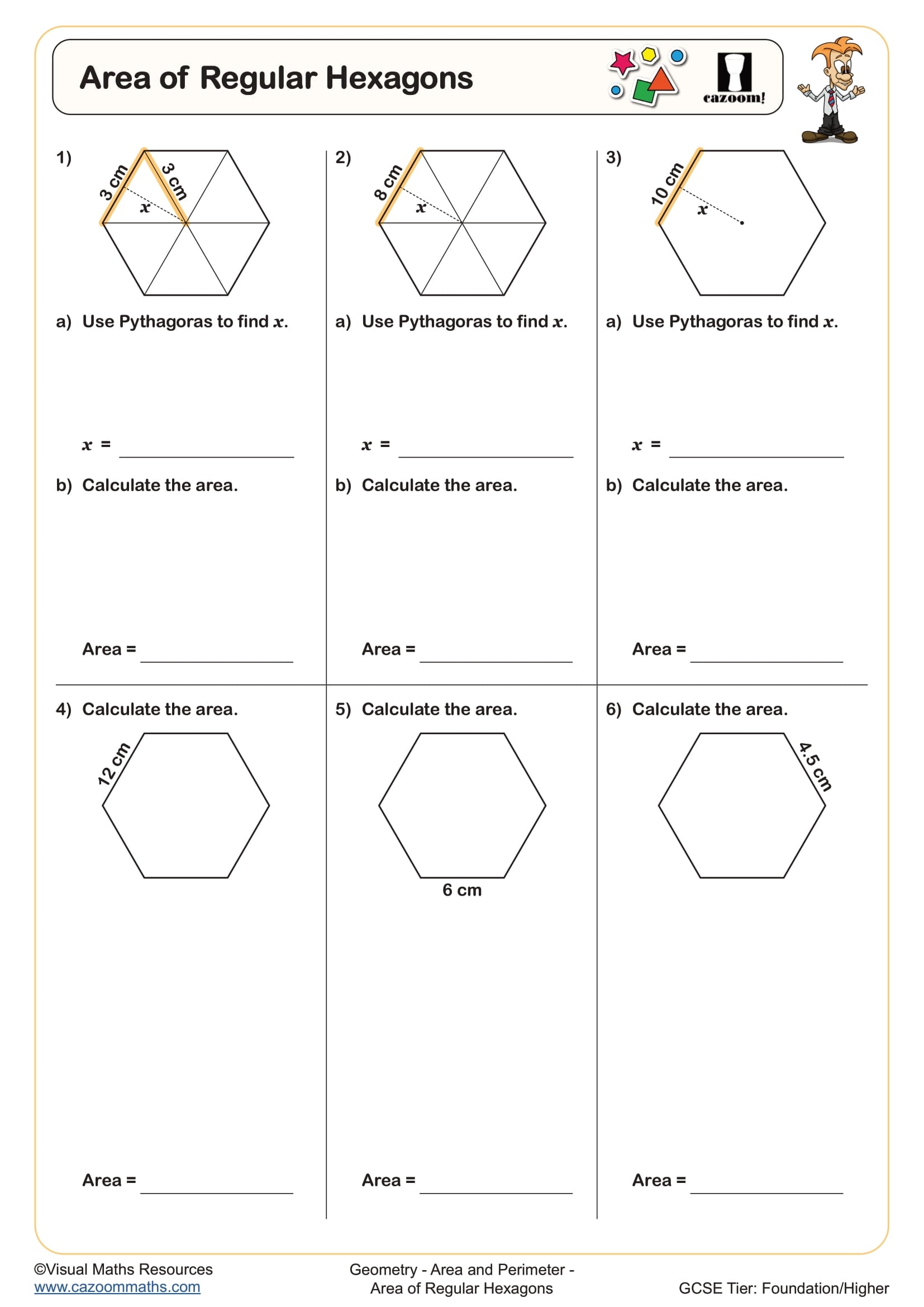
Area of Regular Hexagons

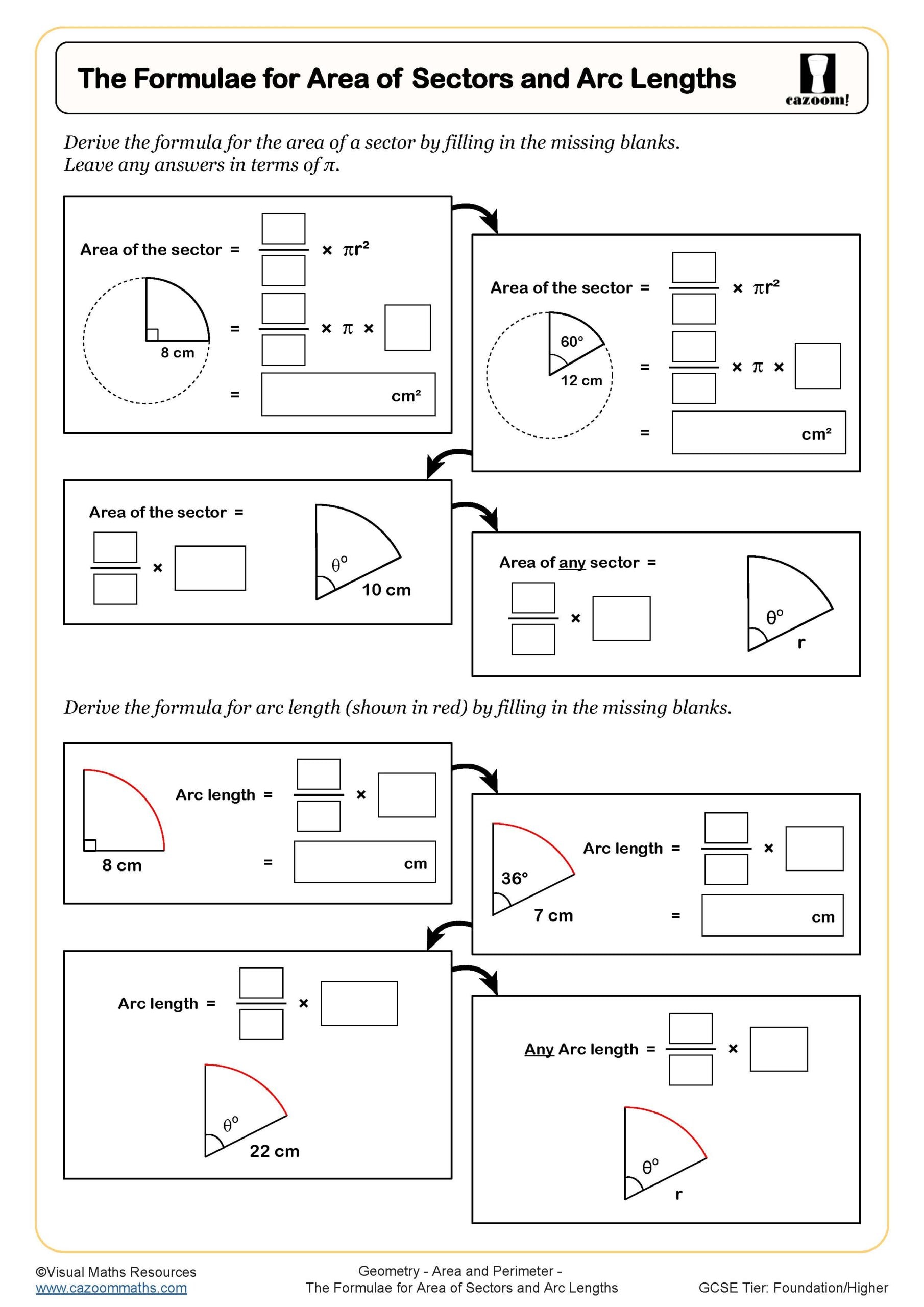
Area of Sectors and Arc Lengths

Area of Sectors and Segments

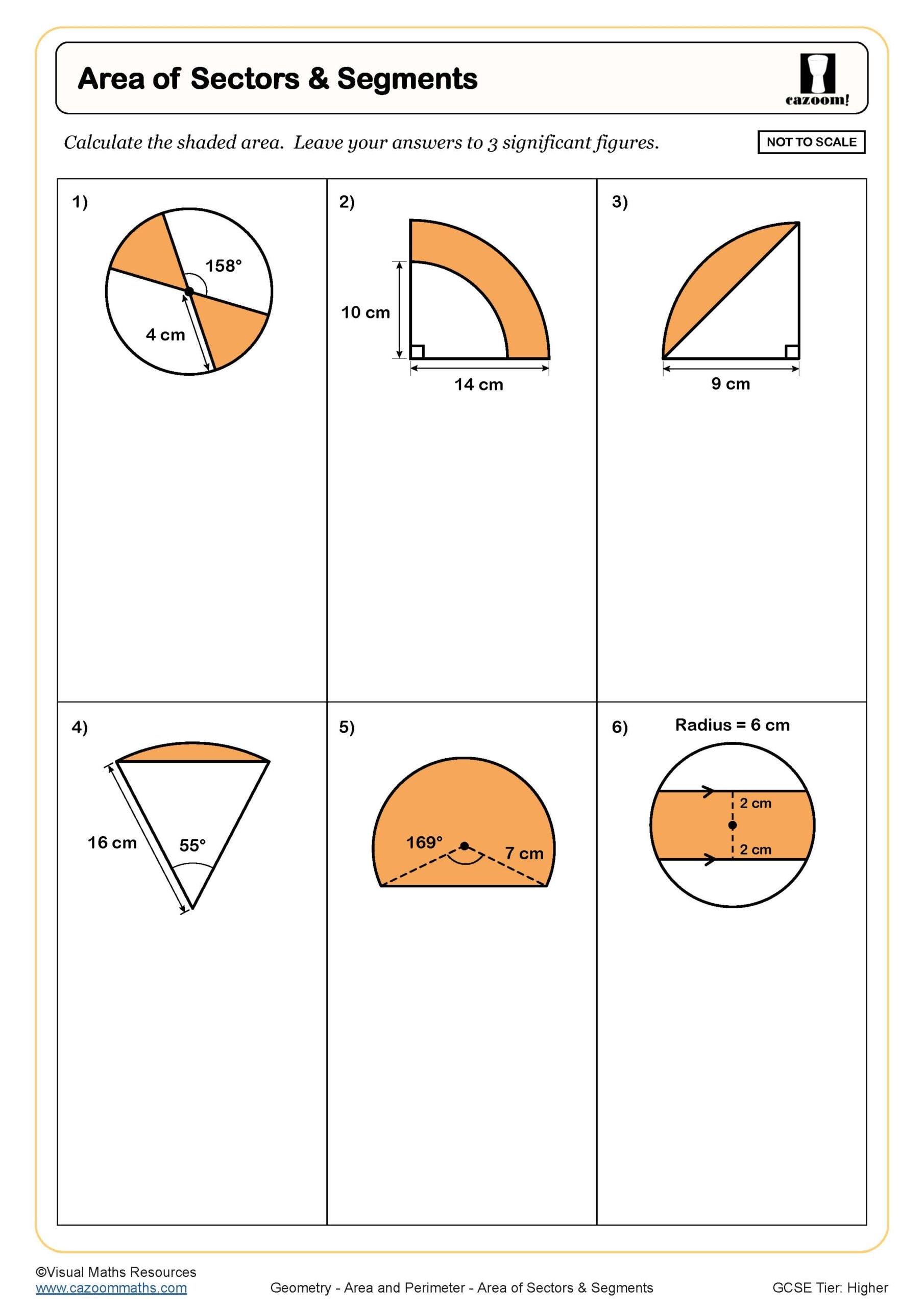
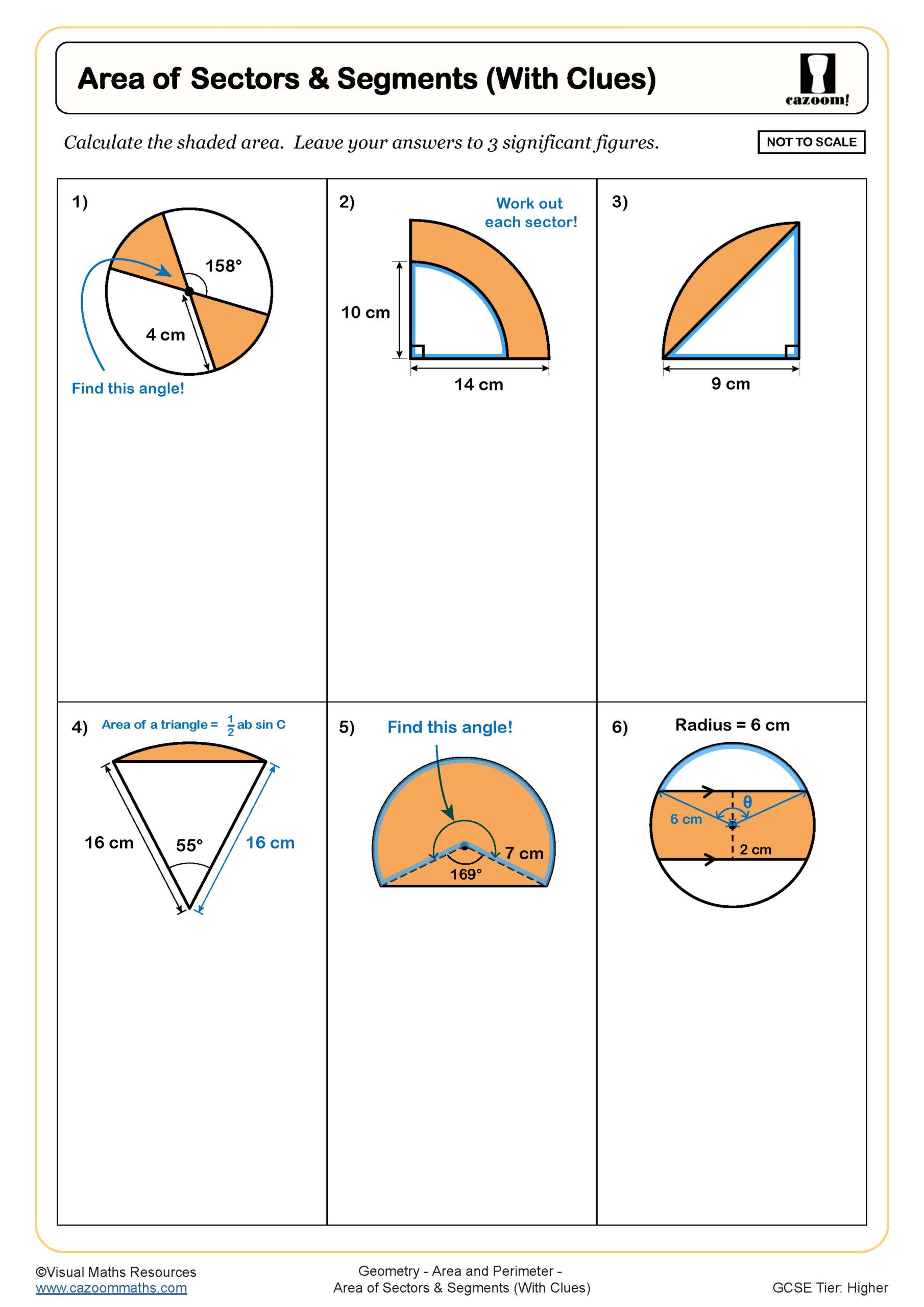
Area of Sectors and Segments (With Clues)

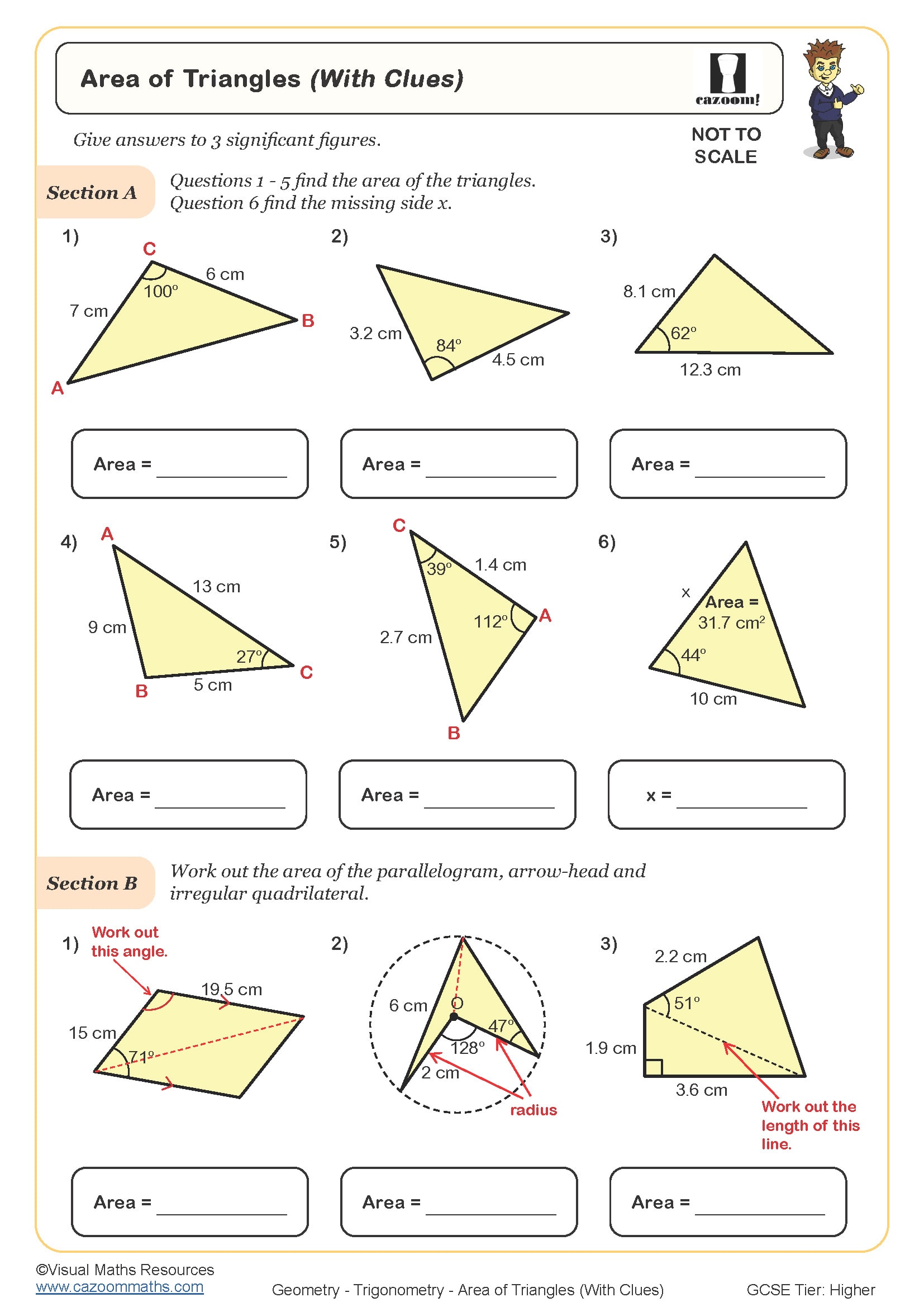
Area of Triangles (With Clues)

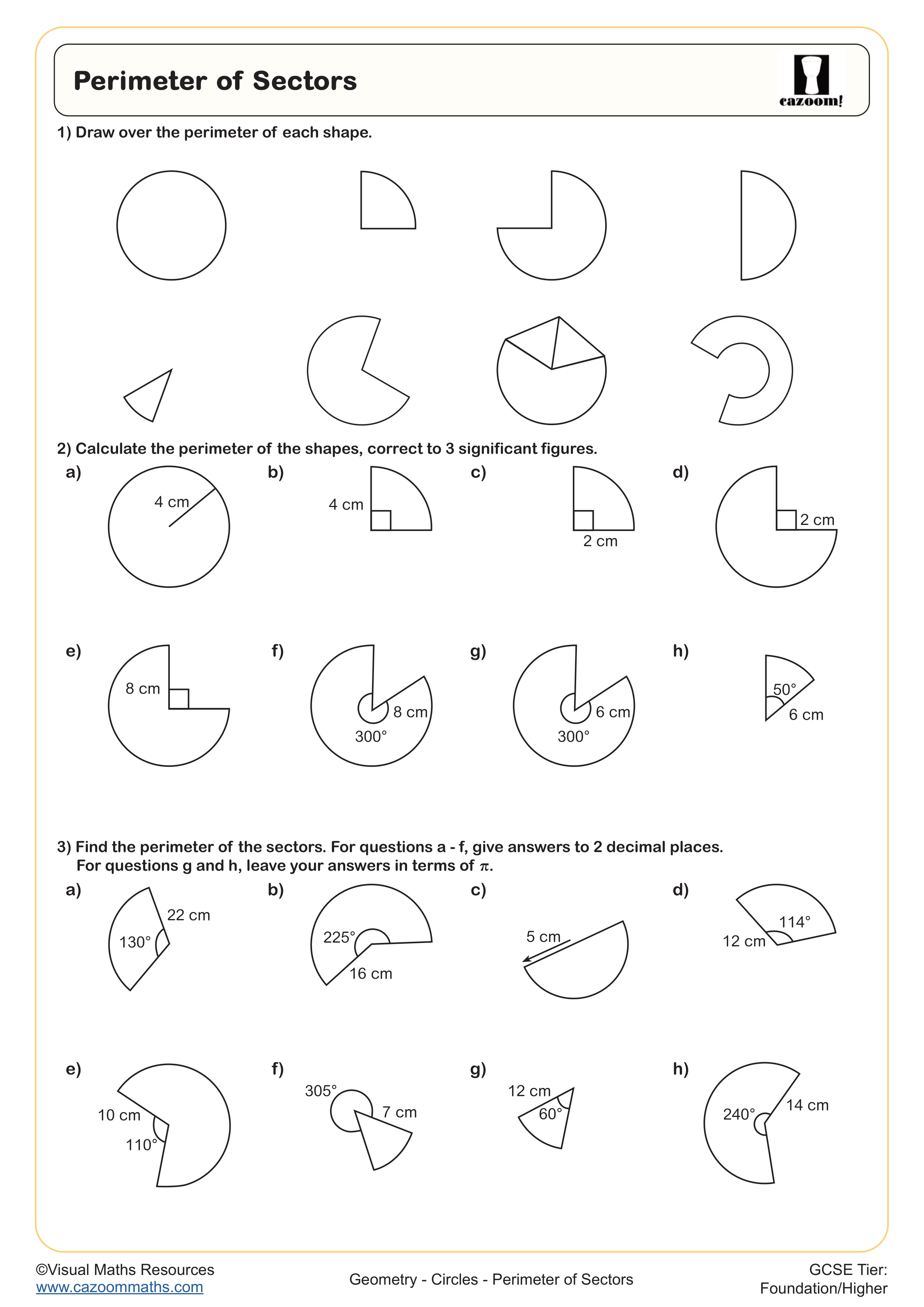
Perimeter of Sectors

Perimeter Using Pythagoras' Theorem

The Formulae for Area of Sectors and Arc Lengths

What area and perimeter topics do Year 11 students need to master for GCSE?

Year 11 students must consolidate all area and perimeter content from earlier key stages whilst tackling GCSE-specific applications. This includes perimeter of compound shapes, circles, sectors and arcs, alongside area calculations for triangles, quadrilaterals, circles, sectors, trapeziums and composite figures. Higher tier students also work with exact answers involving π and reverse problems where they calculate dimensions from given areas or perimeters.

Exam mark schemes expect students to show clear method marks, particularly when breaking composite shapes into manageable components. Students lose marks when they forget to include units, round too early in multi-step problems, or fail to recognise that some shapes require subtraction rather than addition to find areas. The difference between perimeter and area remains a surprisingly common error even at Year 11, especially under exam pressure.

Are these worksheets suitable for both Foundation and Higher tier GCSE students?

These Year 11 area and perimeter worksheets cover content required across both GCSE tiers, with progression built into the question difficulty. Foundation tier students focus on standard shapes, compound rectilinear figures, circles and straightforward problem-solving, whilst Higher tier questions incorporate algebraic perimeters, optimisation problems, and exact answers involving surds or π in fractional form.

The worksheets scaffold difficulty appropriately for GCSE preparation, starting with retrieval of basic formulas before moving into multi-step problems that mirror exam-style questions. Teachers often use these resources to differentiate within mixed-ability groups, selecting specific questions rather than entire sheets, or assigning different worksheets based on whether students are targeting Foundation grade 5 or Higher tier grades. This flexibility makes them valuable for tailoring revision to individual student needs in the final months before exams.

How do you calculate the perimeter of composite shapes?

Calculating perimeter of composite shapes requires students to identify all external edges and add their lengths together, being careful not to include any internal divisions used for area calculations. The key skill is recognising which measurements are missing and using properties of shapes to deduce them—for example, opposite sides of rectangles being equal, or using Pythagoras' theorem to find slant heights in shapes containing right-angled triangles.

This skill connects directly to real-world applications in construction and design, from calculating fencing required for irregularly shaped gardens to determining the length of skirting board needed in L-shaped rooms. Architects and engineers regularly work with composite perimeters when designing floor plans, calculating material quantities, or determining thermal efficiency boundaries in building regulations. Understanding how to break complex shapes into manageable sections is a fundamental problem-solving strategy across STEM disciplines.

How can teachers use these worksheets most effectively for GCSE revision?

The worksheets work well as diagnostic tools at the start of revision cycles, helping teachers identify which specific formulas or shape types individual students struggle with. Because complete answer sheets are provided, students can attempt questions independently and self-assess, developing the exam skill of checking answers for reasonableness—a valuable habit when calculator errors or formula mistakes occur under exam conditions.

Many teachers use these resources for spaced retrieval practice, revisiting area and perimeter concepts at intervals throughout Year 11 rather than in a single revision block. They're particularly effective for homework when paired with video revision resources, allowing students to refresh their understanding before attempting questions. In intervention sessions, teachers often work through one or two questions as a class before students tackle similar problems independently, using the answer sheets to provide immediate feedback and address misconceptions before they become embedded.