Year 11 Compound Measures Worksheets
What are compound measures in maths?
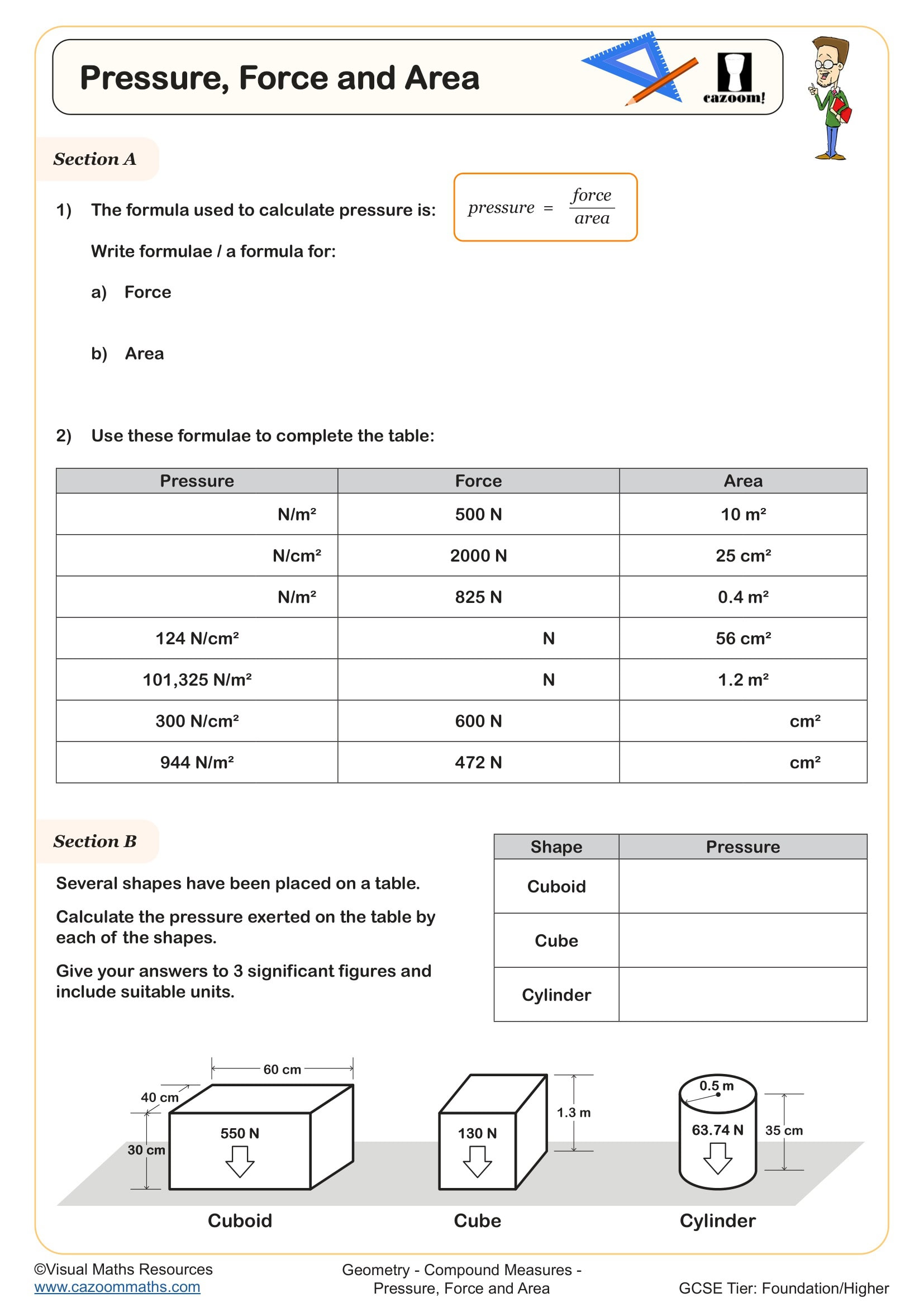
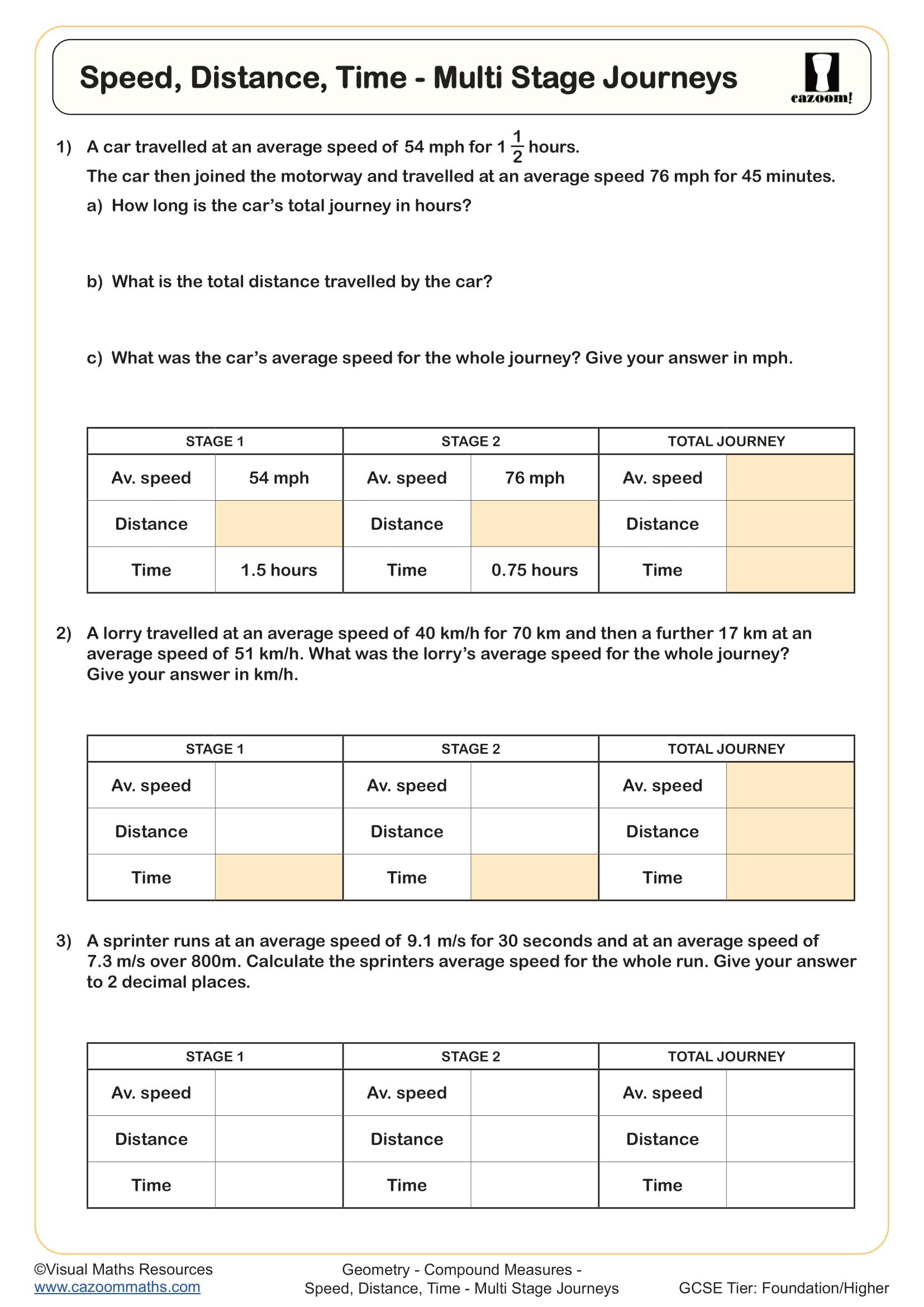
Compound measures combine two or more basic measurements to create a new measure with practical applications. The three key examples in the GCSE curriculum are speed (distance per unit time), density (mass per unit volume) and pressure (force per unit area). Students encounter these from Year 8 onwards, but Year 11 focuses on more complex problem-solving and rearranging formulas to find different variables.
A common error occurs when students attempt to solve problems without identifying units first. For instance, calculating speed when distance is given in kilometres but time in minutes leads to incorrect answers unless students convert to consistent units. Exam mark schemes routinely penalise missing or incorrect units, even when numerical answers are correct, so encouraging students to write units at every calculation stage helps avoid lost marks.
Which year groups study compound measures?
These worksheets target Year 11 students at Key Stage 4, typically as part of GCSE revision or final preparation for examinations. Compound measures first appear in Year 8 when students learn the basic formulas for speed, density and pressure, then develop through Years 9 and 10 with increasingly complex scenarios involving unit conversions and multistep problems.
By Year 11, the focus shifts to exam-style questions that combine compound measures with other topics such as ratio, proportion and algebraic manipulation. Students work with less straightforward scenarios where they must rearrange formulas, convert between metric and imperial units, or solve problems embedded in extended written contexts. This progression builds the problem-solving resilience needed for higher-tier GCSE papers.
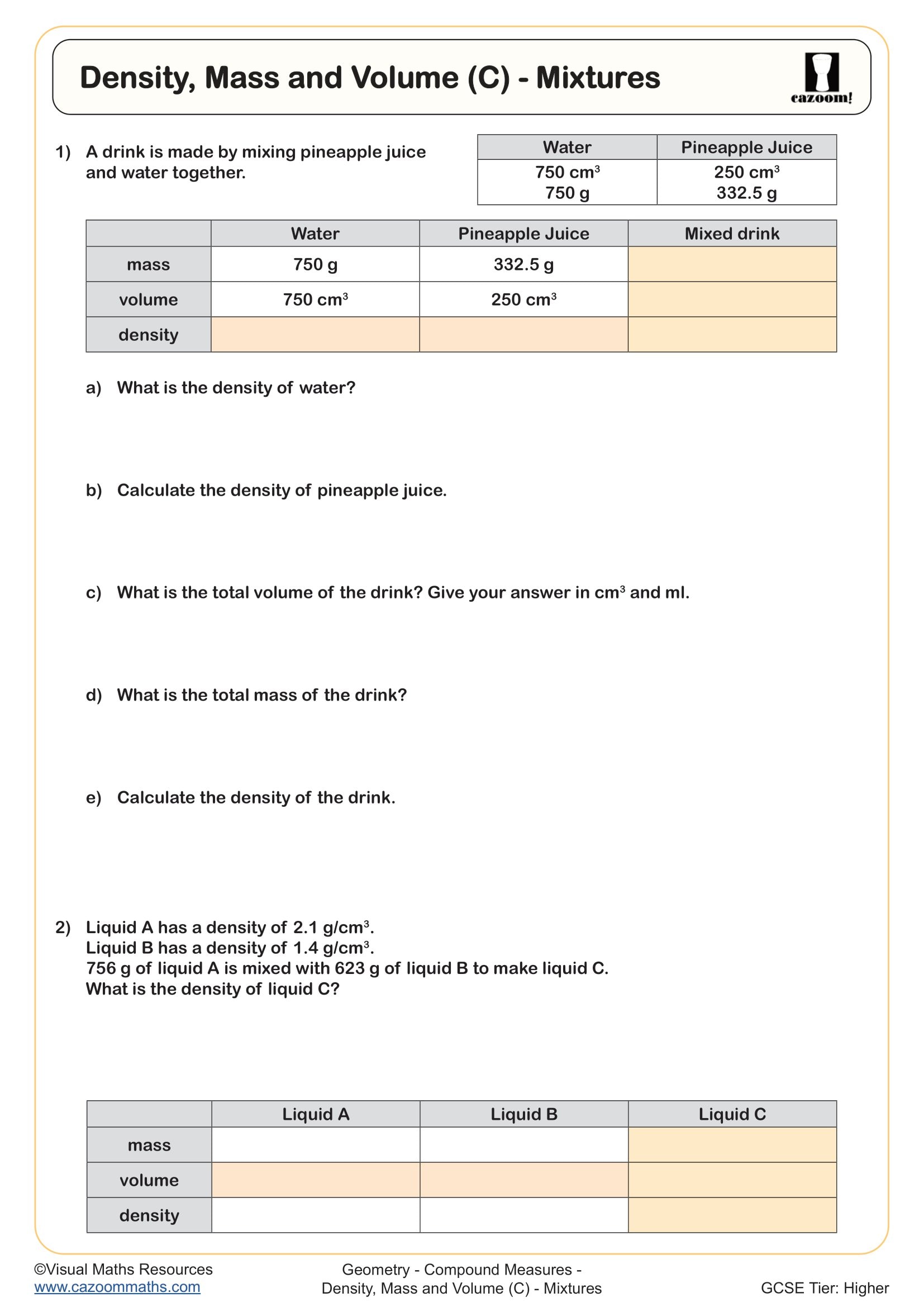
How do you calculate density in different units?
Density calculations use the formula density equals mass divided by volume, but the units depend entirely on the context of the question. Students might work in grams per cubic centimetre for small objects, kilograms per cubic metre for larger items, or even tonnes per cubic metre in engineering contexts. The key skill involves identifying which units the question requires and converting the given measurements accordingly before dividing.
Density appears throughout STEM subjects, from materials science to environmental studies. Engineers select construction materials based on density to balance strength against weight in structures like bridges and aircraft. In chemistry, understanding density explains why oil floats on water and helps students predict whether substances will sink or float. These real-world connections help students appreciate why precision with units matters beyond simply passing examinations.
How can teachers use these worksheets effectively?
The worksheets build from straightforward formula application through to multistep problems requiring unit conversions and formula rearrangement. This structure allows teachers to identify precisely where individual students struggle, whether with basic calculations, selecting appropriate formulas, or managing more complex problem-solving. The included answer sheets show complete working, not just final answers, which helps students understand the logical steps required.
Many teachers use these resources for targeted intervention with students who find word problems challenging, as compound measures questions always embed calculations within real-world contexts. The worksheets work well for homework following classroom teaching, as independent practice with formula triangles and unit conversions. During revision periods, students can work through problems in pairs, discussing which formula applies and checking their reasoning against the worked solutions before moving to exam papers.