Year 11 Transformations Worksheets
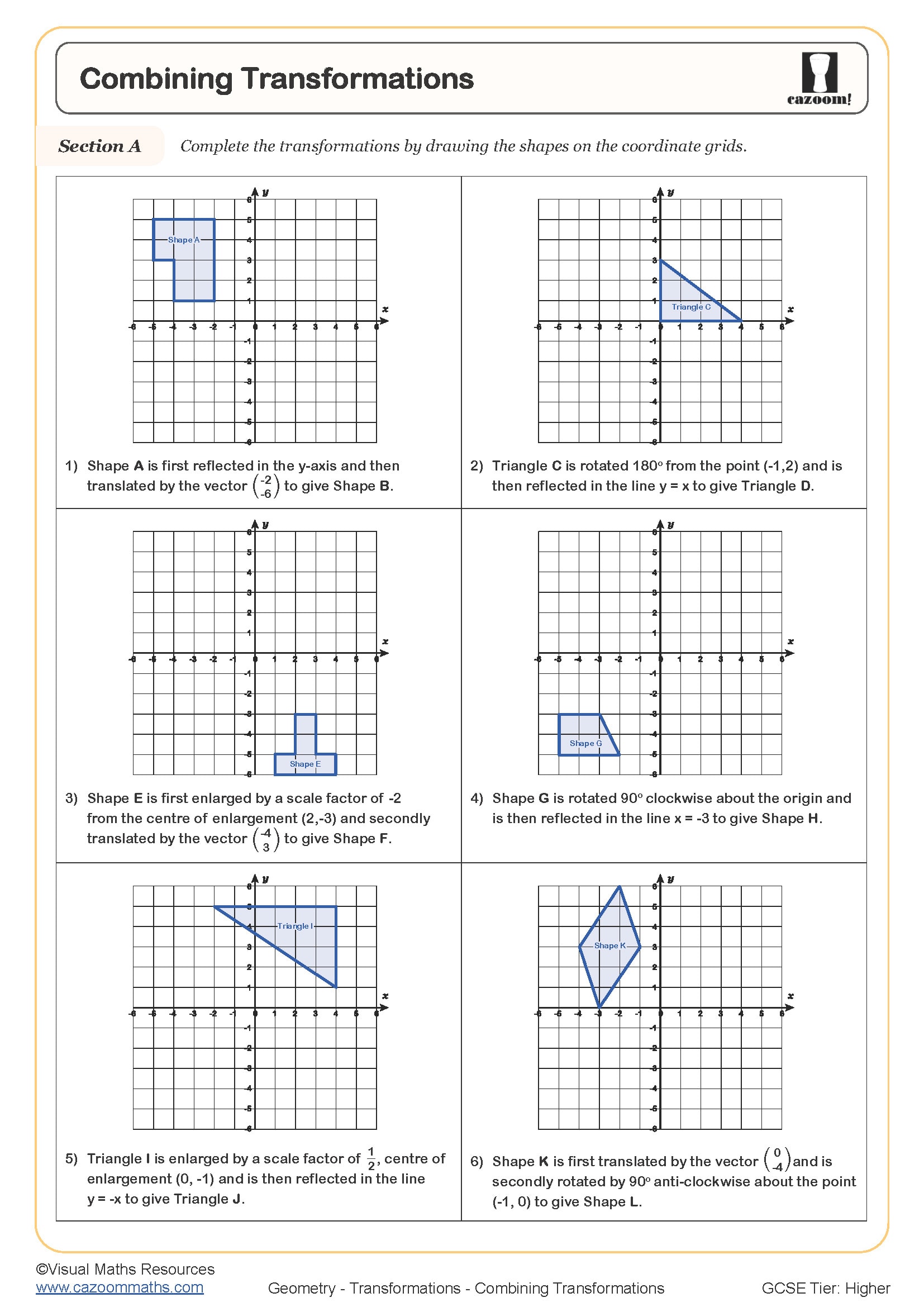
Combining Transformations
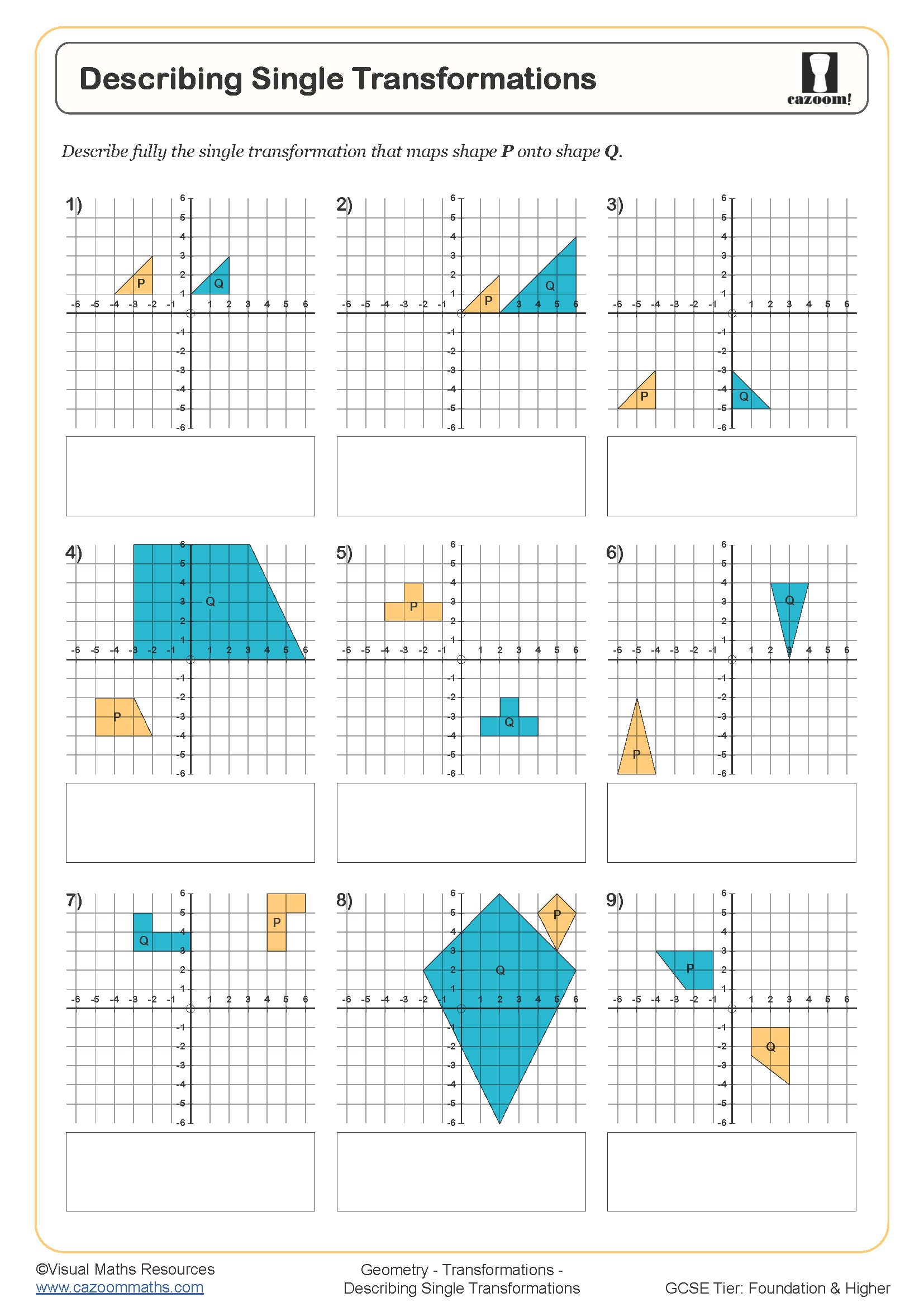
Describing Single Transformations
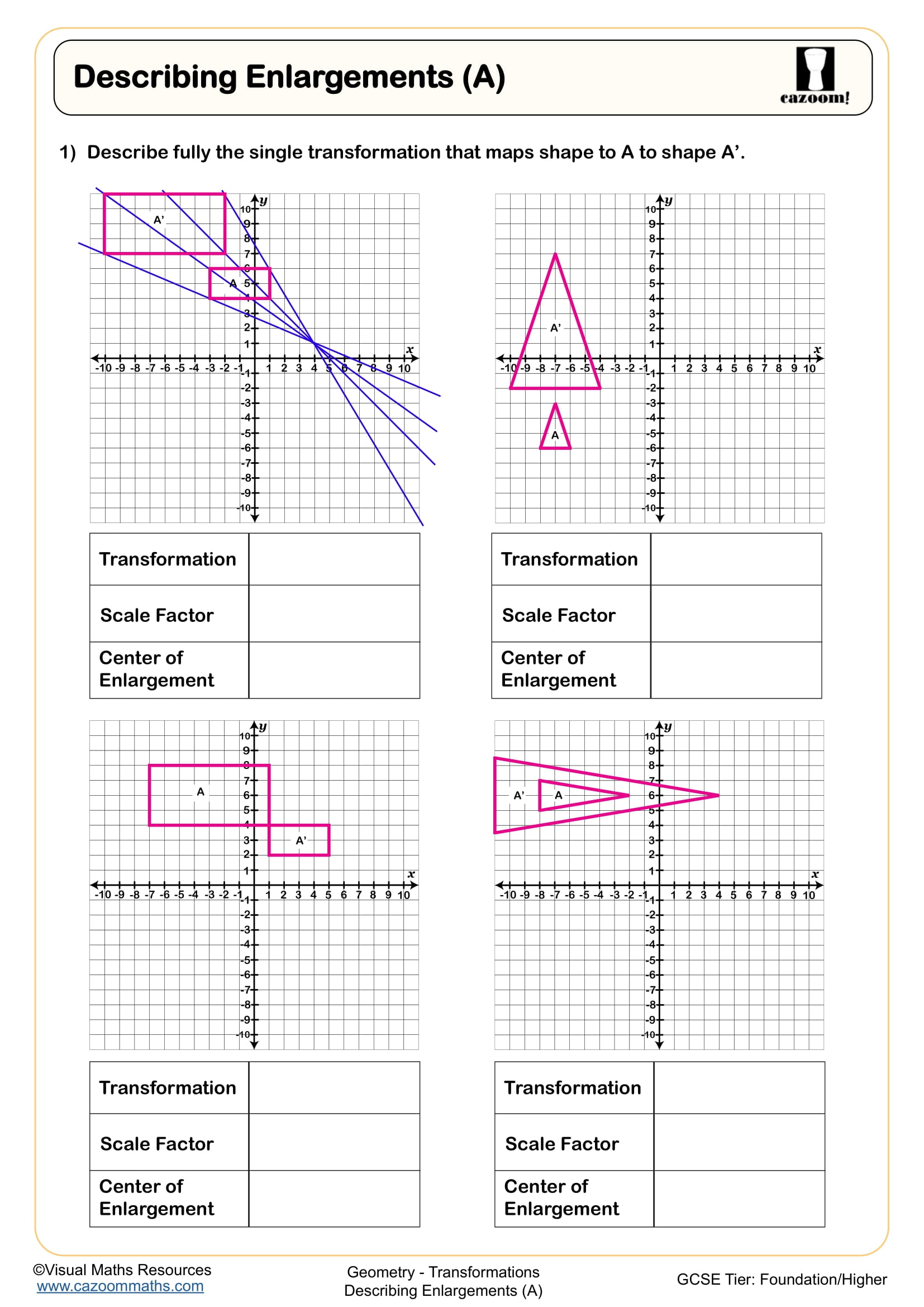
Describing Enlargements (A)
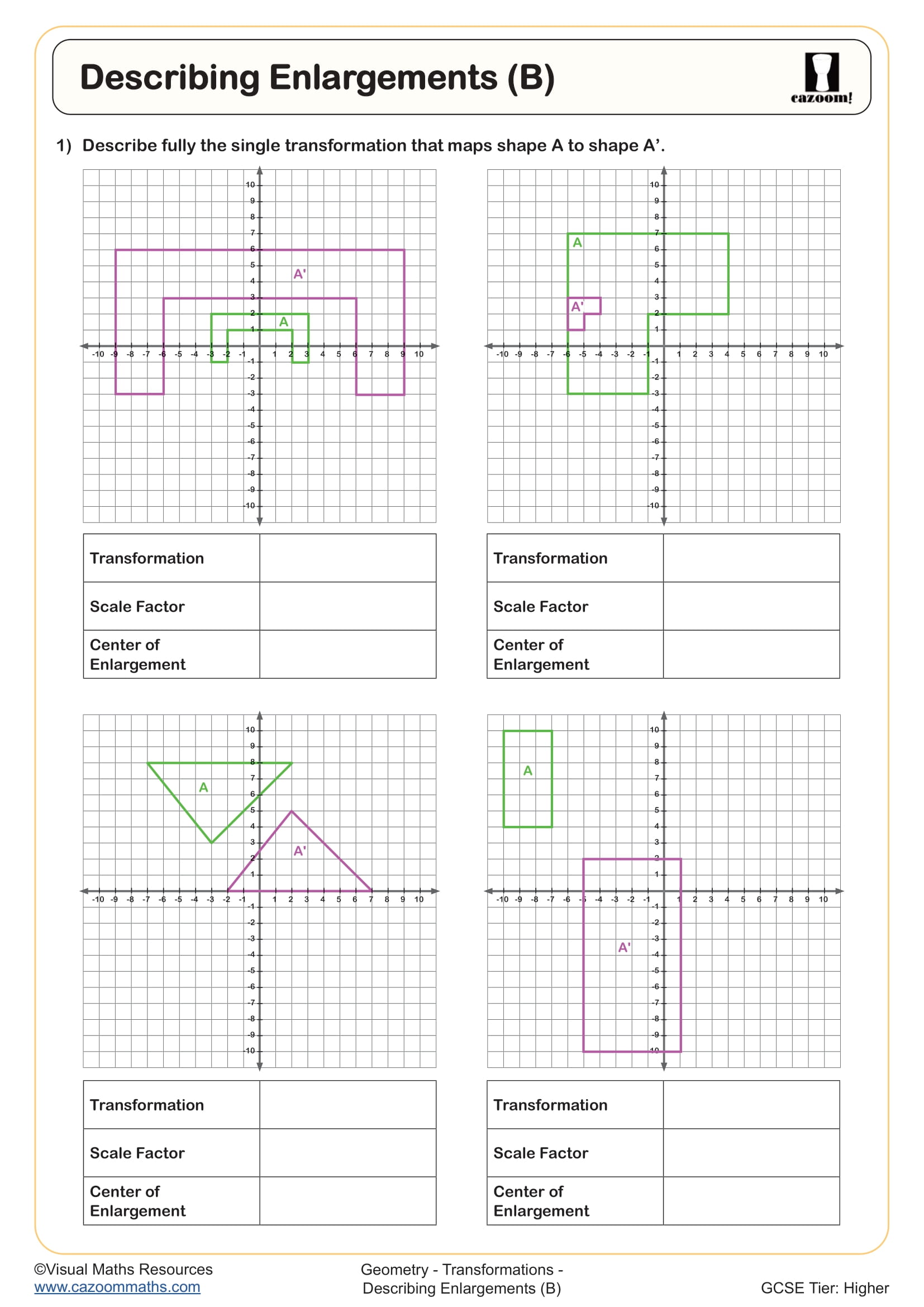
Describing Enlargements (B)
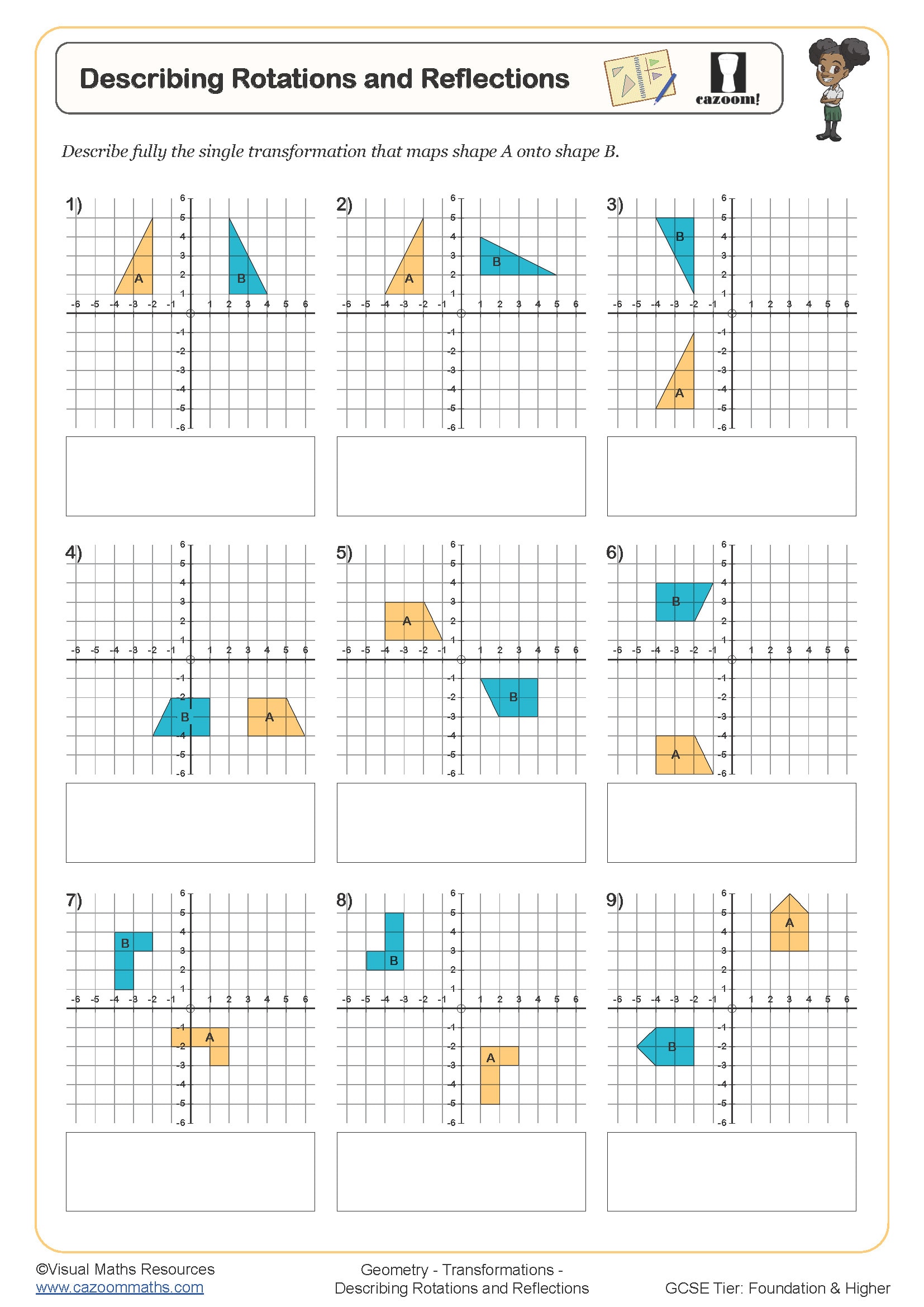
Describing Rotations and Reflections
Enlargement (C)
-Worksheet.jpg)
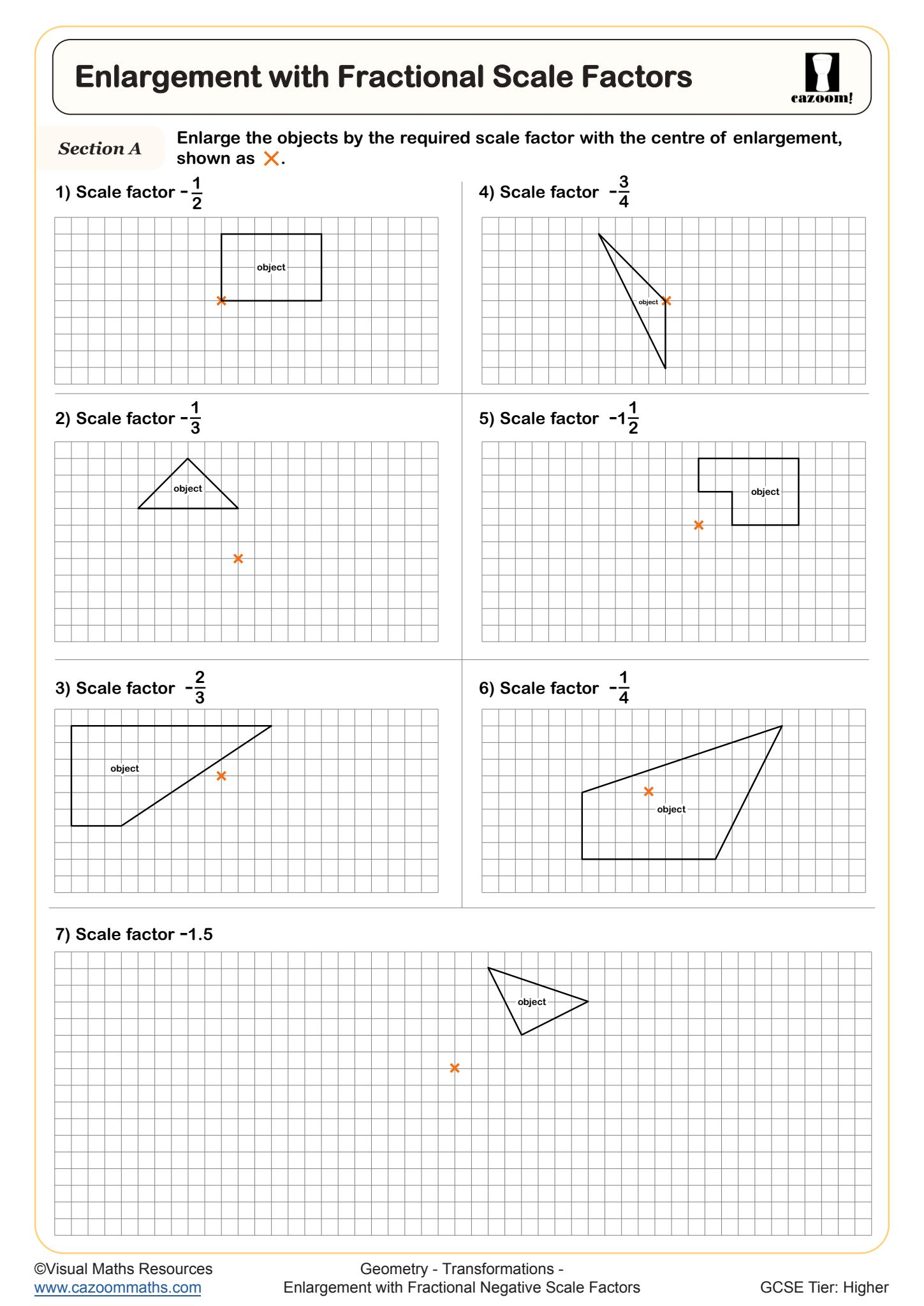
Enlargement with Fractional Negative Scale Factors
Enlargement with Fractional Scale Factors (A)
-Worksheet.jpg?w=3840)
Enlargement with Fractional Scale Factors (B)
-Worksheet.jpg?w=3840)
Enlargement with Negative Scale Factors

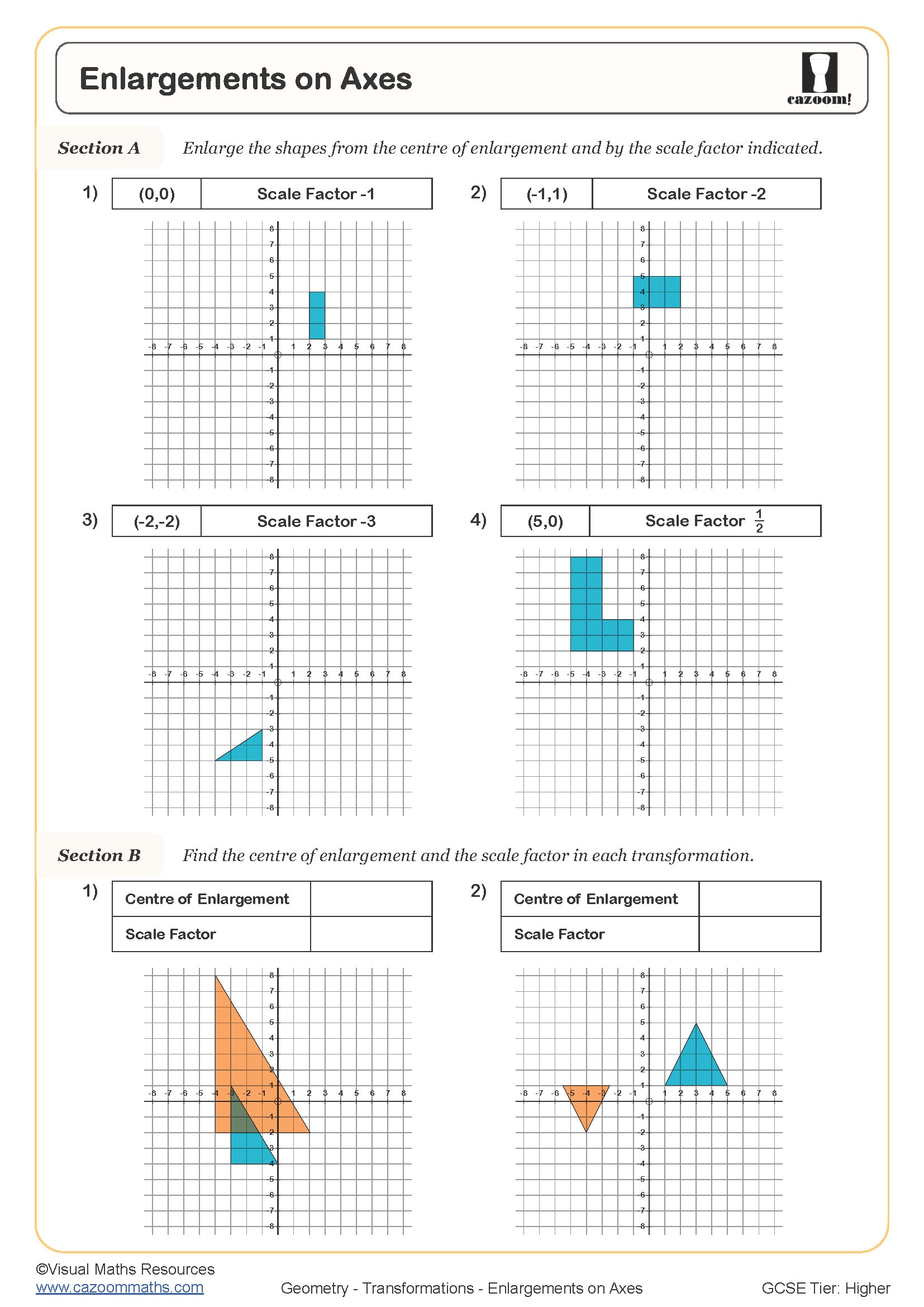
Enlargements on Axes
Enlargements Using Column Vectors

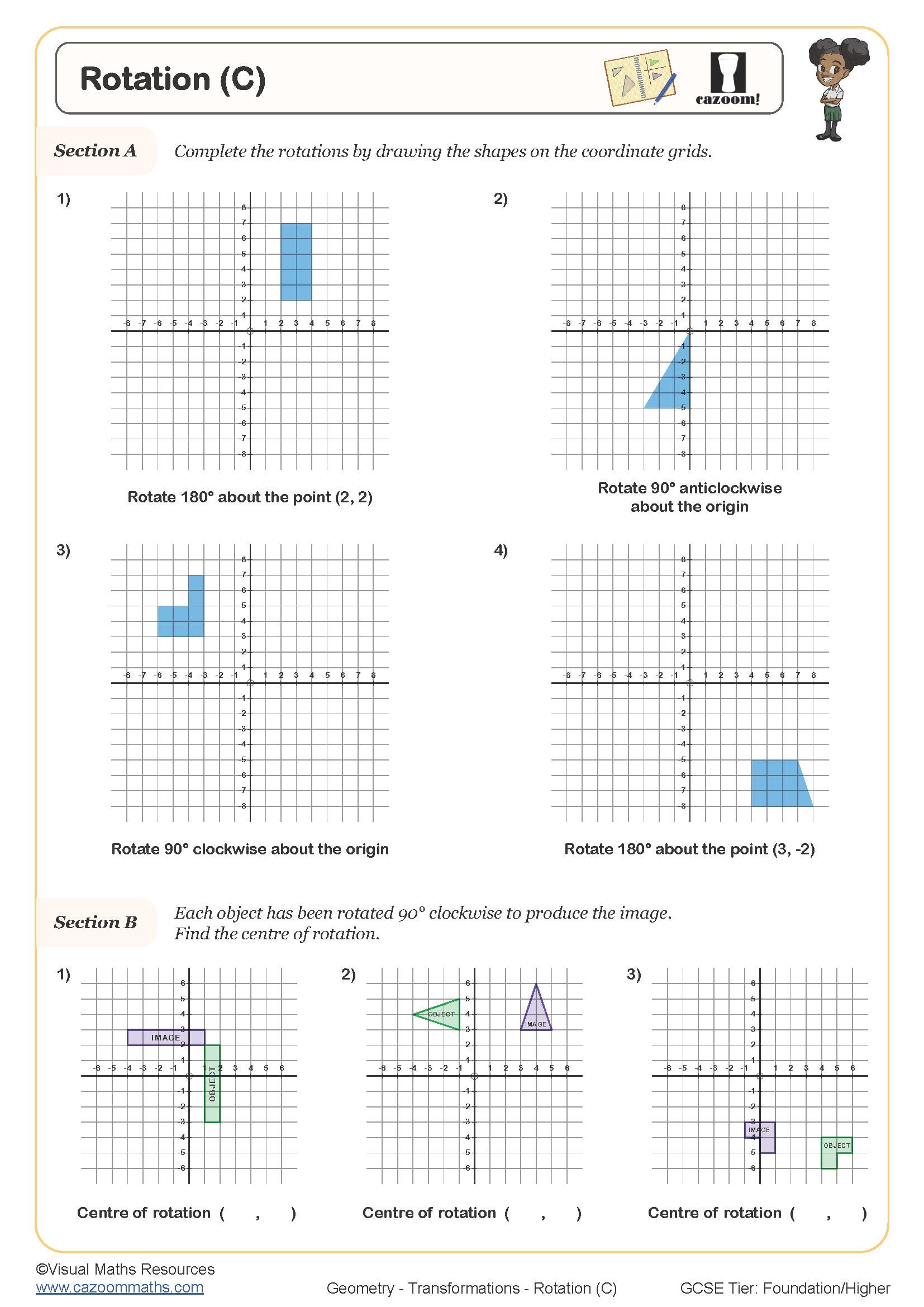
Rotation (C)
Scale Factors and Centres of Enlargement (A)

Scale Factors and Centres of Enlargement (B)

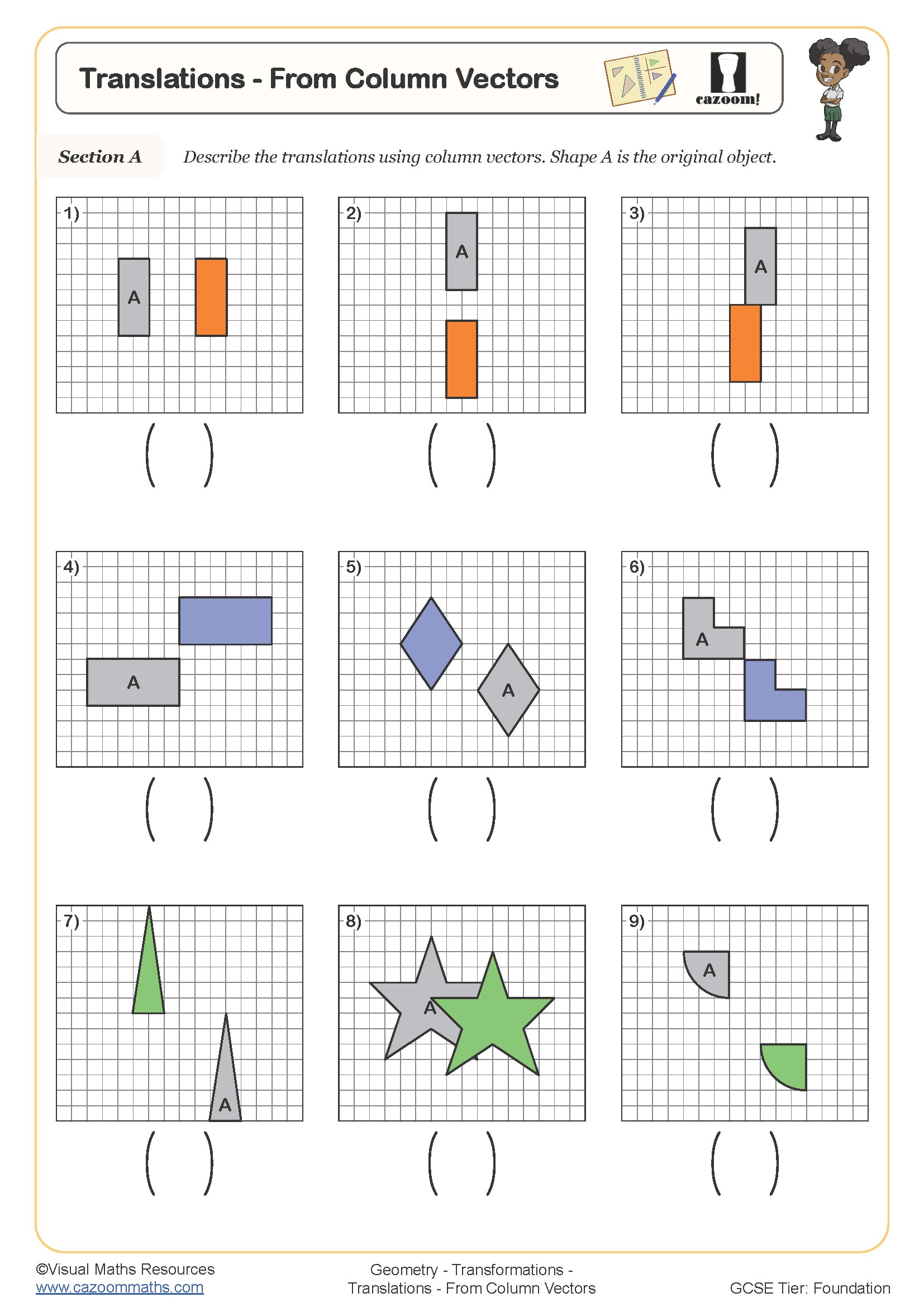
Translations - from Column Vectors
Essential Transformations Worksheets PDF Downloads That Build Real Understanding
We've all been there – spending ages hunting for decent transformation worksheet resources that don't just test memorisation. These Year 11 transformations worksheets with answers focus on building a genuine understanding of translation, rotation, reflection, and enlargement concepts. Each problem is carefully sequenced to develop spatial reasoning skills progressively, with step-by-step solutions that show the thinking process behind each transformation.
Complete Transformations Skills Your Year 11 Students Will Master
We've packed comprehensive coverage into these worksheets! The progression moves smoothly from basic single transformations to complex combined transformations that challenge even confident mathematicians. Students particularly love how the problems connect transformations to coordinate geometry – they're genuinely surprised when patterns emerge.
Our complete collection covers all essential transformation topics for Year 11:
• Single Transformations - Translation vectors, rotation centres and angles, reflection lines, and enlargement scale factors
• Combined Transformations - Sequential transformations and their equivalent single transformations
• Coordinate Geometry Applications - Transformations on the coordinate plane with algebraic representations
• Transformation Matrices - Introduction to matrix representations of transformations
• Invariant Points and Lines - Understanding what remains unchanged during transformations
• Transformation Equations - Algebraic descriptions of transformations and their inverses
• Real-World Applications - Computer graphics, design patterns, and architectural symmetry
• GCSE Exam Practice - Question formats and mathematical language that appear in assessments
Transform Year 11 Geometry Results with Targeted Practice
Here's what we've noticed over the years of teaching: students who get regular, focused practice with transformations perform significantly better in GCSE geometry questions. The connection between consistent practice and exam confidence is remarkable to watch. These worksheets target the exact skills that appear in assessment papers, giving students crucial familiarity with question formats and mathematical language.
Key benefits teachers consistently report:
• Improved spatial visualisation skills are essential for advanced mathematics
• Enhanced coordinate geometry confidence is needed for A-Level preparation
• Stronger pattern recognition that applies across multiple math topics
• Better exam technique through structured practice opportunities
• Reinforced algebraic thinking through transformation equations
Where Transformation Skills Connect - Applications Students Actually Encounter
Students always ask, "When will we ever use this?" – and with transformations, we've got exciting answers! These skills appear in subjects they're already studying and careers they're considering. Computer graphics and game design rely heavily on transformation mathematics, which gets students genuinely excited about possibilities they hadn't considered.
Transformations connect directly to:
• Computer graphics, animation, and game development
• Architecture and engineering design for structural planning
• Art, textile design, and pattern creation
• Physics and engineering for understanding motion and forces
• Medical imaging technology, like MRI and CT scan interpretation
• Navigation and GPS systems for route calculation and positioning
• Psychology and visual perception studies
• Geography and map projections