Year 11 Volume and Surface Area Worksheets

These Year 11 volume and surface area worksheets provide targeted practise on the 3D shape calculations that feature heavily in GCSE Higher tier papers. Students work through questions on surface area of pyramids and spheres, alongside volume calculations that require applying formulae accurately and interpreting composite shapes. Teachers frequently notice that students confuse surface area with volume when tackling exam questions under pressure, particularly when questions don't explicitly state which measurement to find. Each worksheet in this collection includes complete answer sheets as PDF downloads, allowing students to check their working independently and identify where calculation errors occur. The progression across these resources builds confidence with the formulae and problem-solving approaches that exam mark schemes reward.

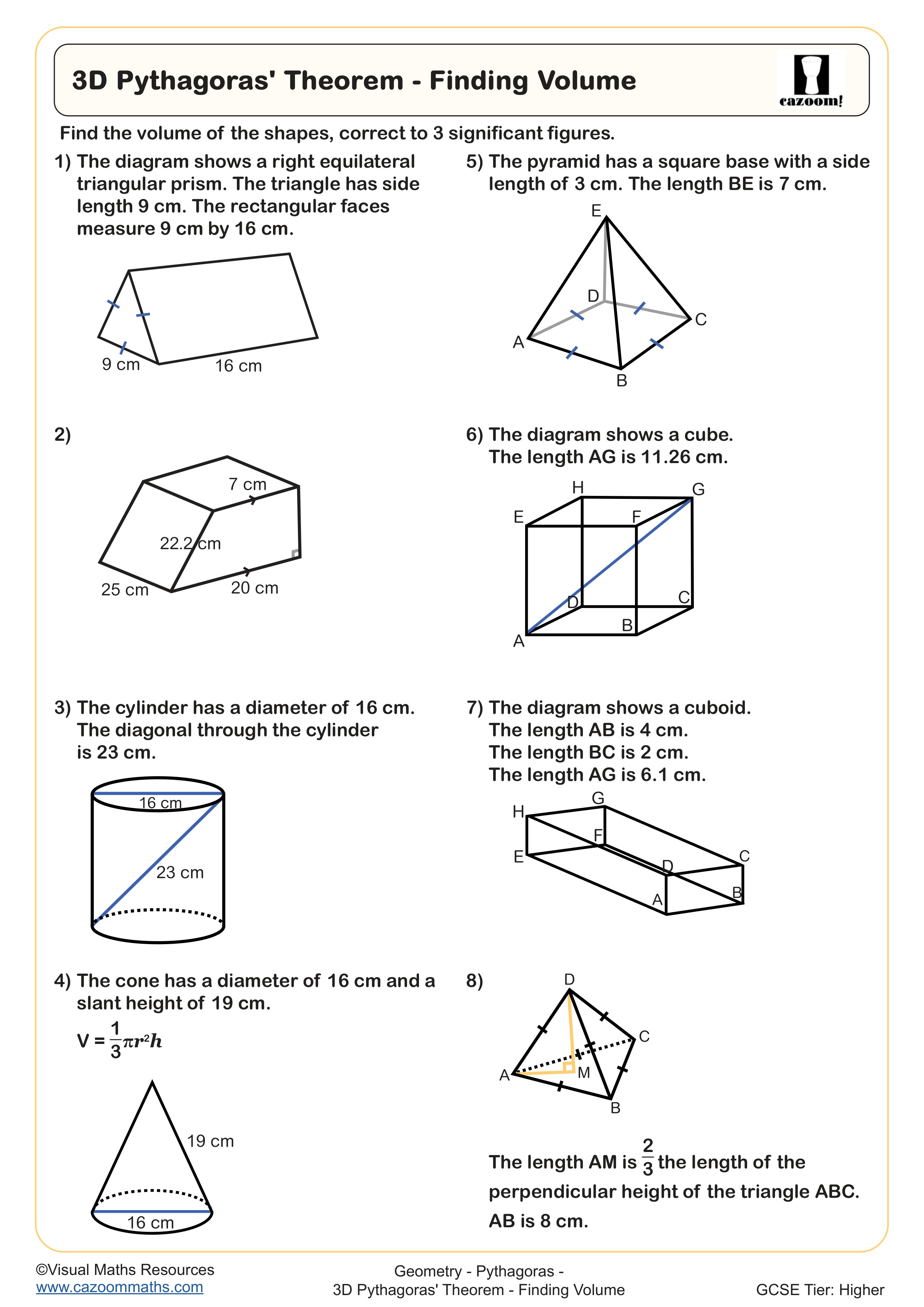
3D Pythagoras' Theorem - Finding Volume

Area and Volume of Similar Shapes (A)

Area and Volume of Similar Shapes (B)

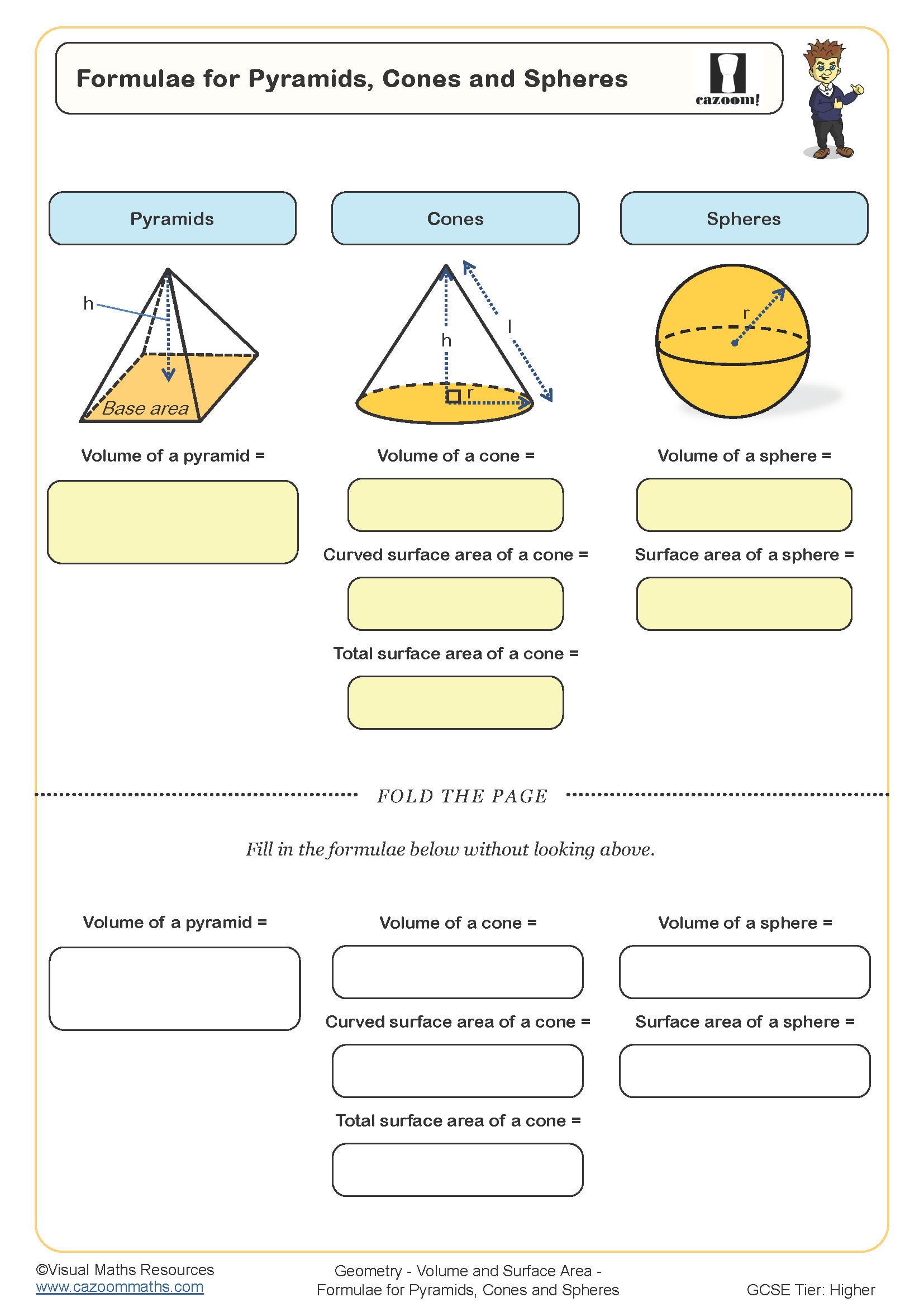
Formulae for Pyramids Cones and Spheres

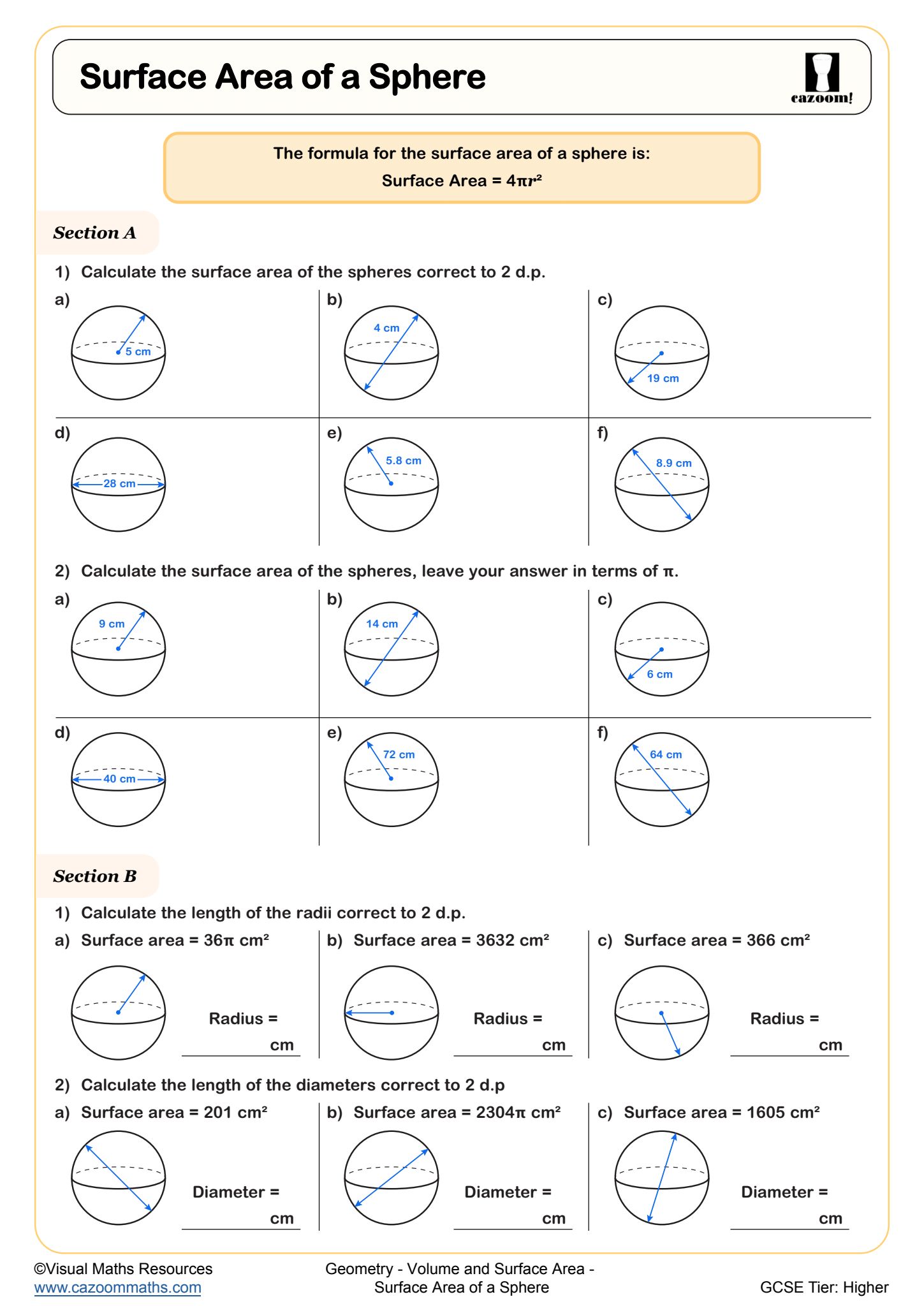
Surface Area of a Sphere

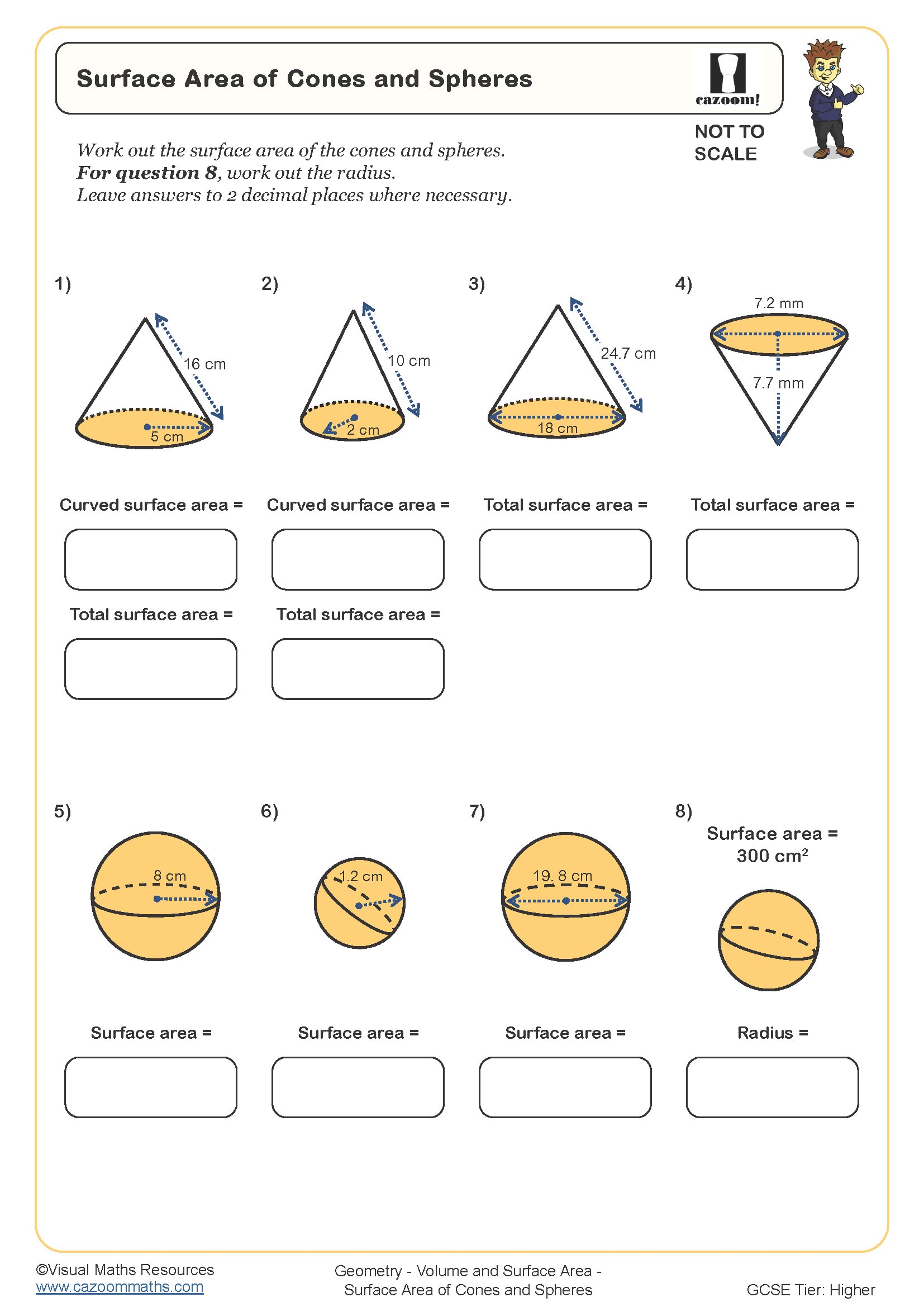
Surface Area of Cones and Spheres

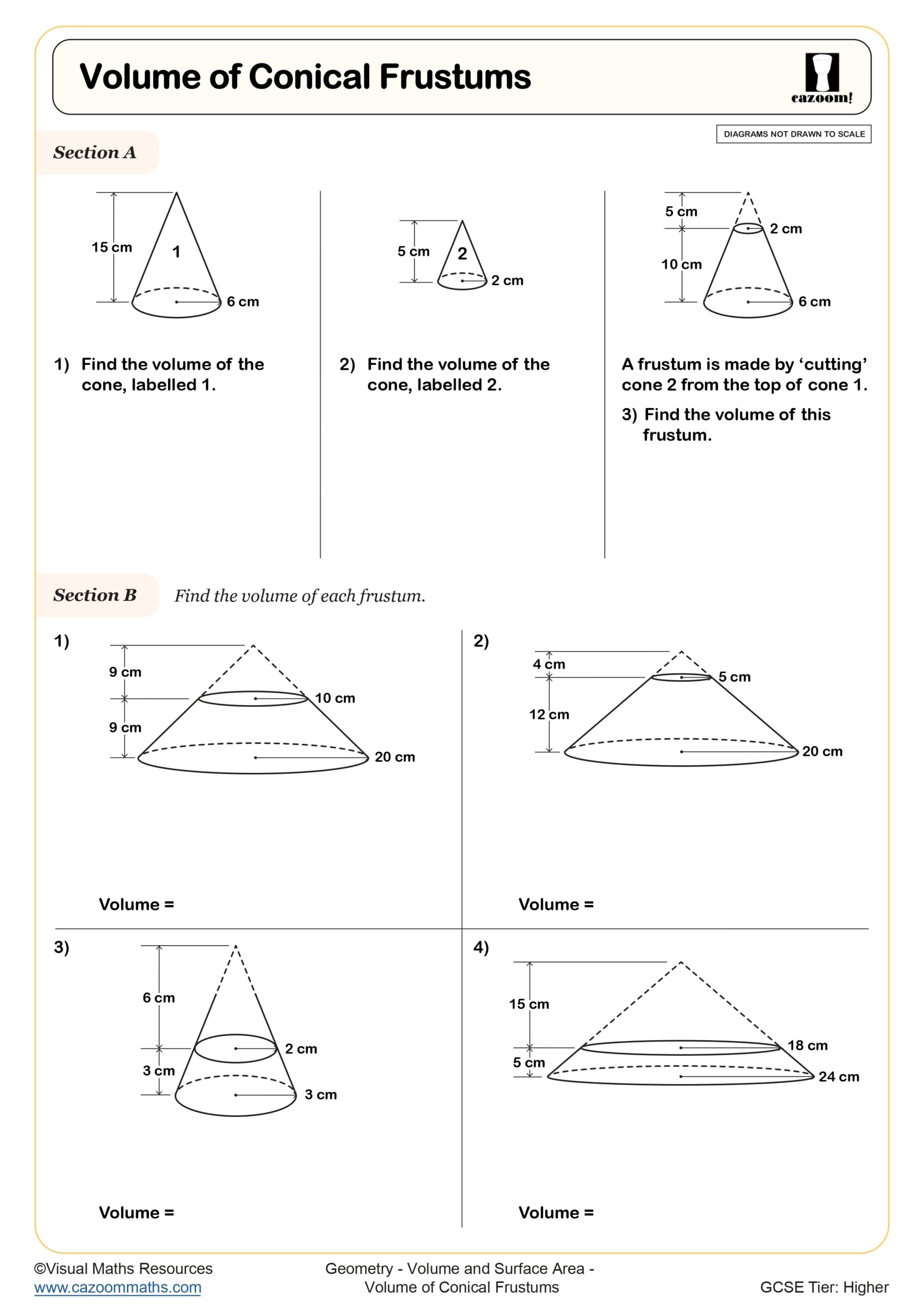
Surface Area of Conical Frustums

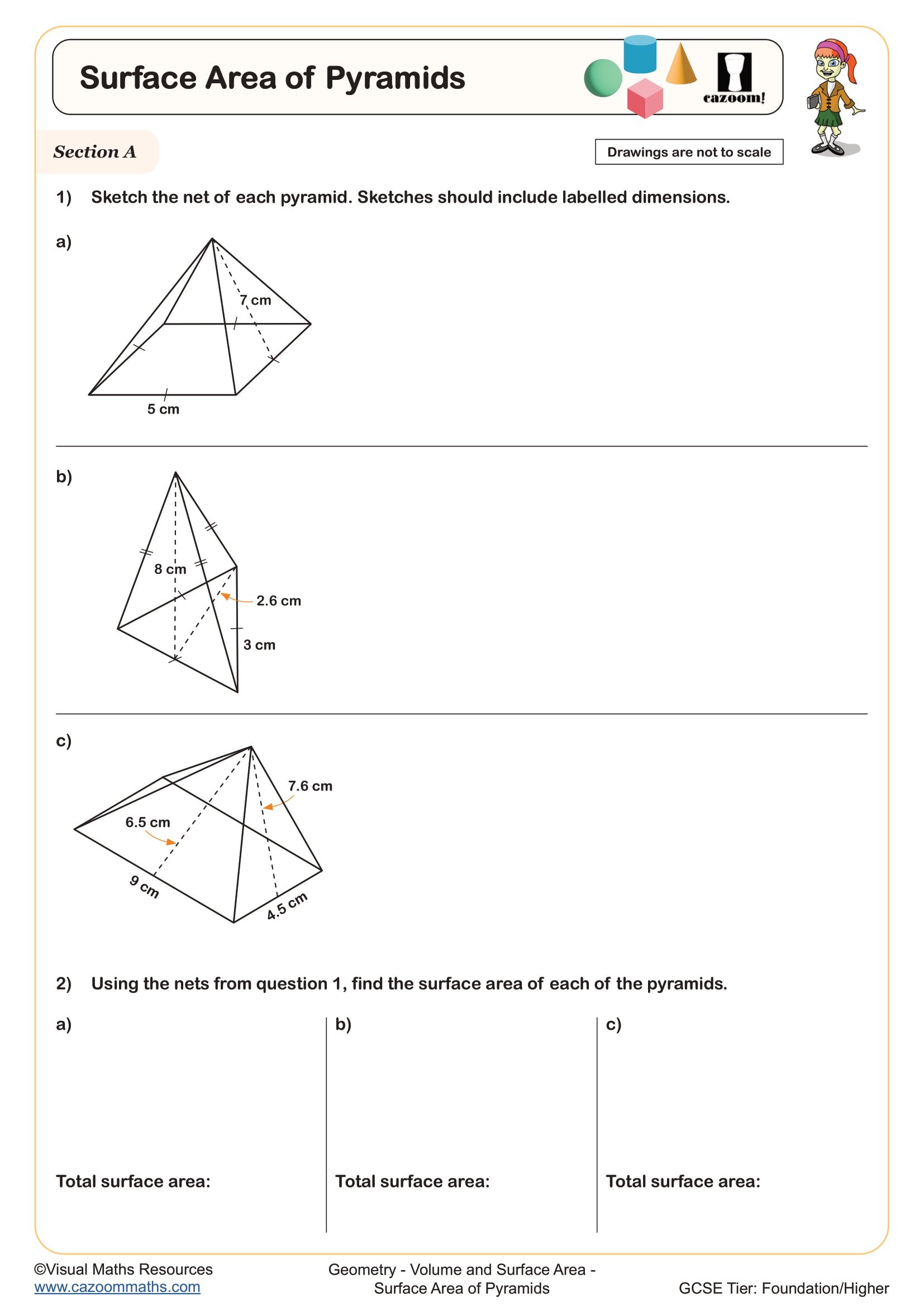
Surface Area of Pyramids

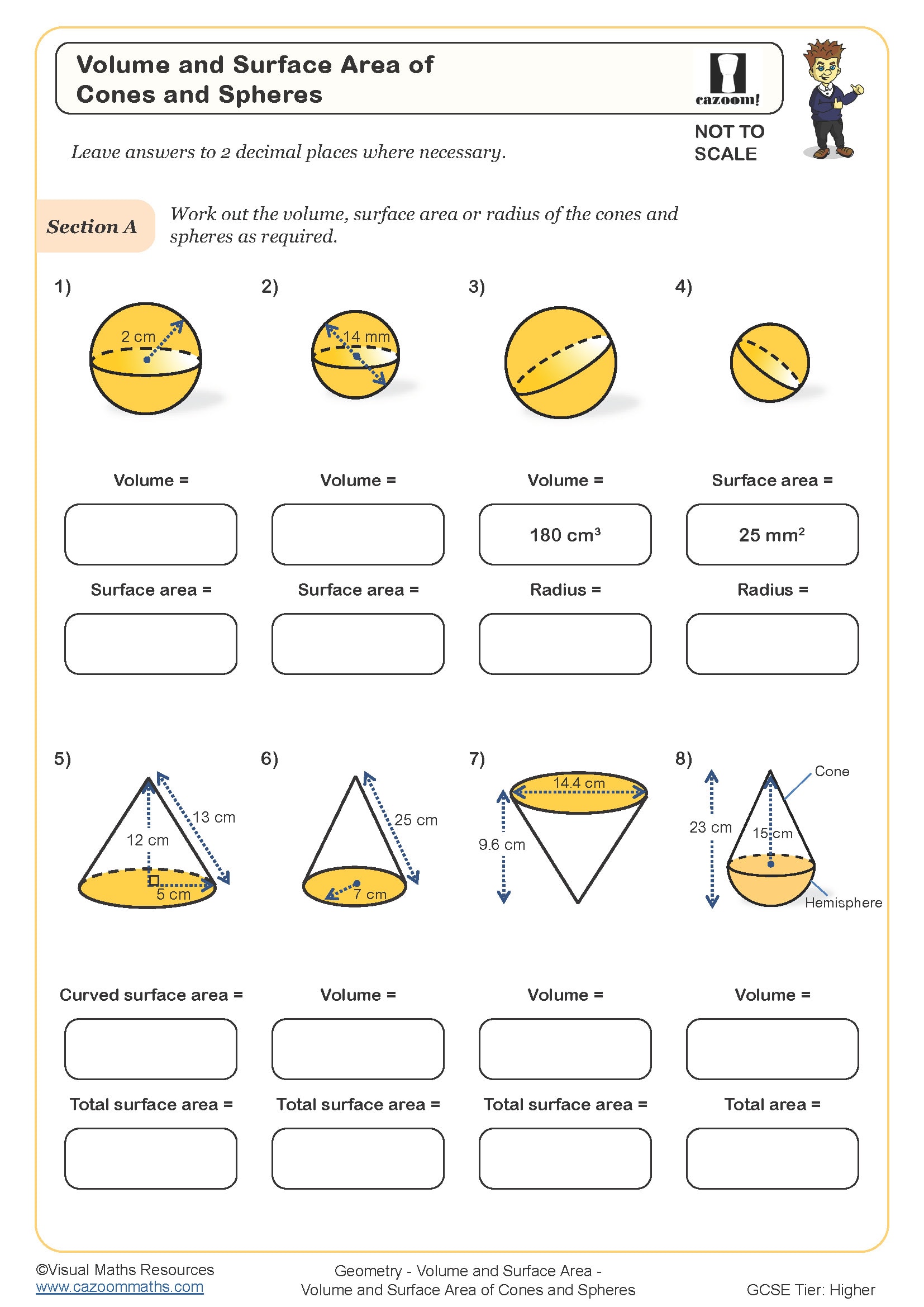
Volume and Surface Area of Cones and Spheres

Volume of a Cone

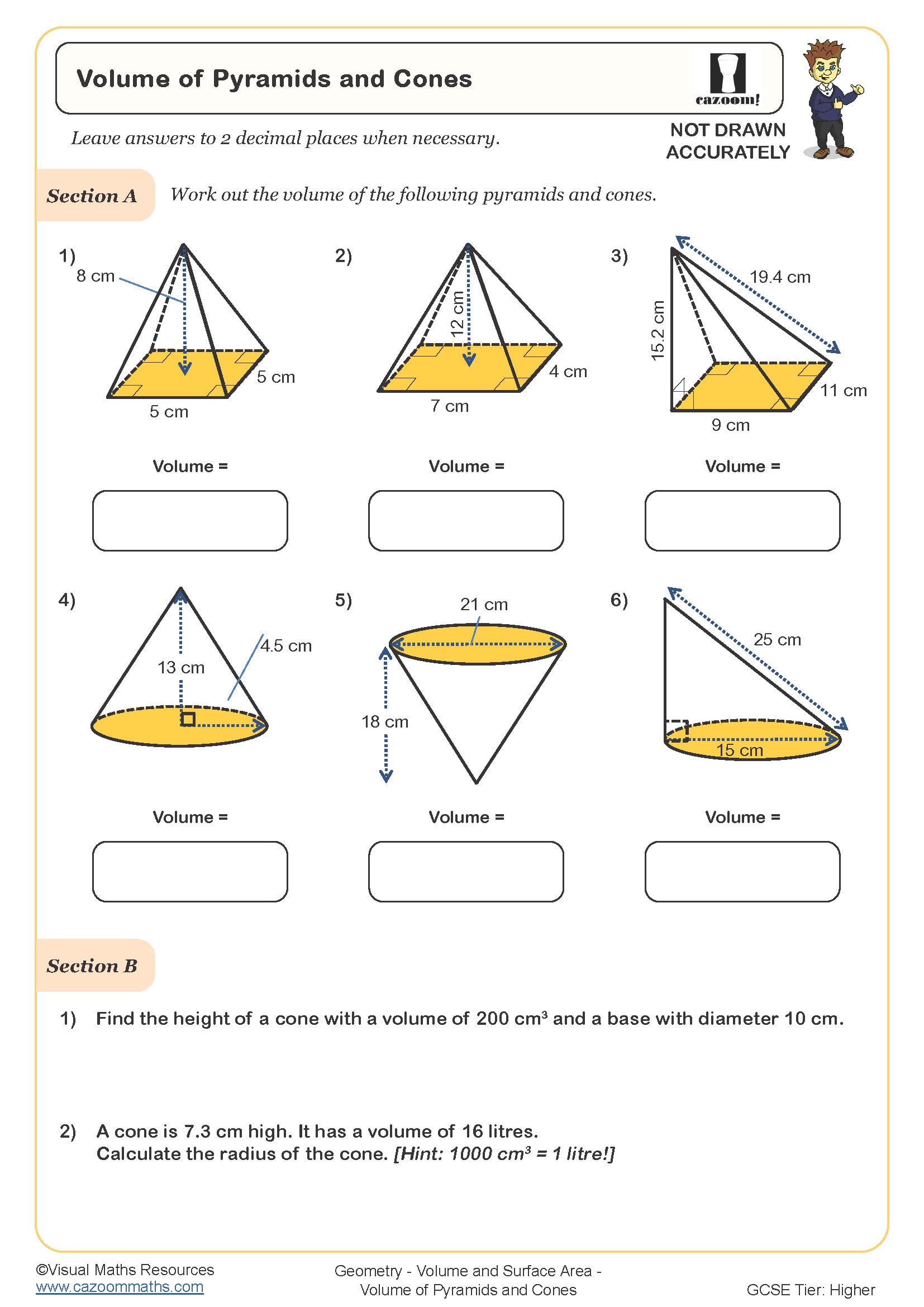
Volume of a Pyramid

Volume of a Sphere

Volume of Conical Frustums

Volume of Pyramids and Cones

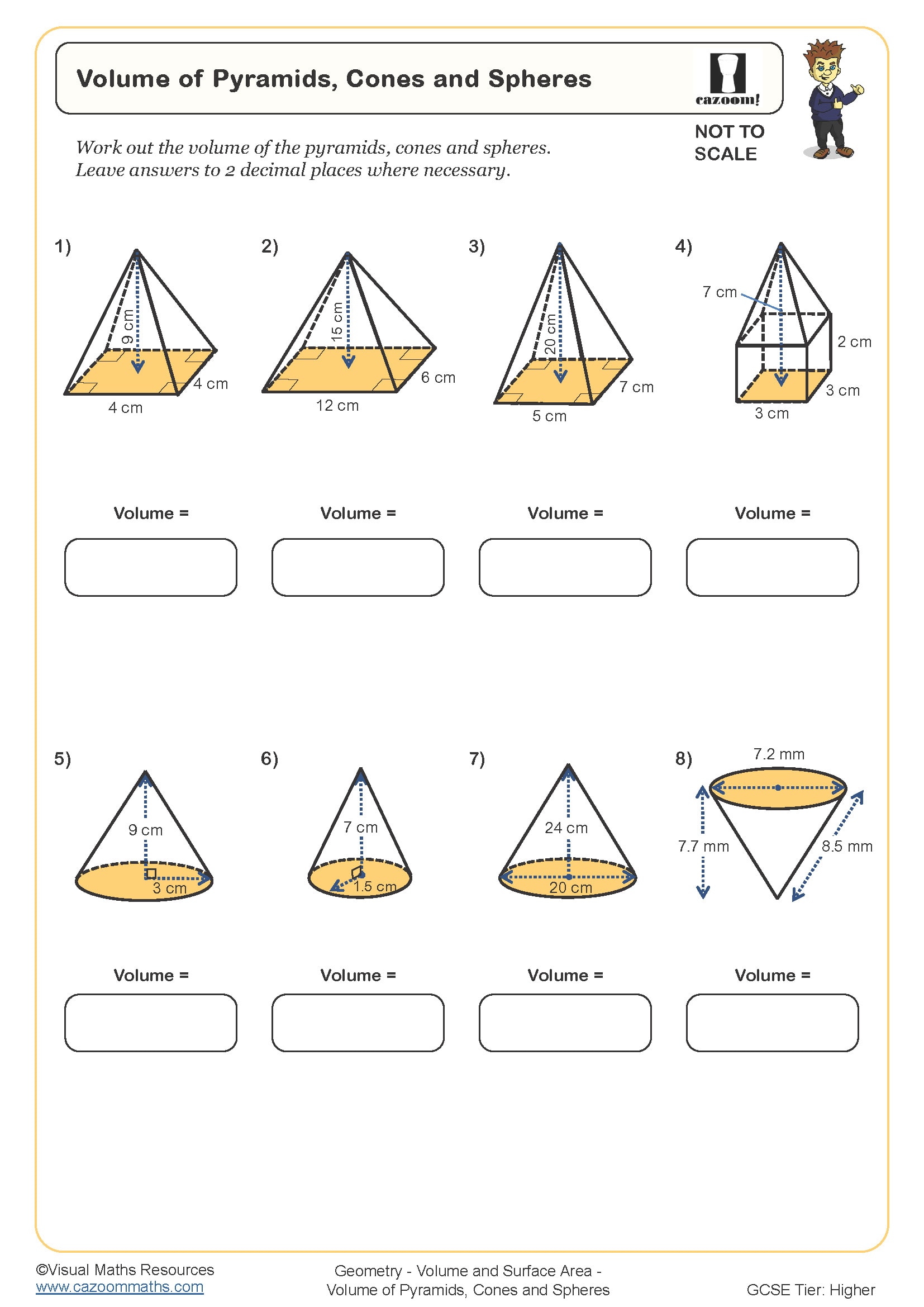
Volume of Pyramids Cones and Spheres

Volume of Square-based Pyramid Frustums

What calculations do students need for volume and surface area at GCSE?

GCSE Higher tier students must calculate both volume and surface area for prisms, pyramids, cones, spheres, and composite solids formed by combining these shapes. The formulae for spheres (volume = 4/3πr³, surface area = 4πr²) and pyramids (volume = 1/3 × base area × height) appear on GCSE formula sheets, but students need practise interpreting which measurements to substitute and when to apply them. Questions often present diagrams where students must first identify relevant dimensions before selecting the appropriate formula.

Students lose marks when they round π too early in multi-step calculations or forget to include all faces when calculating surface area of composite solids. Exam questions frequently test whether students can work backwards from a given volume to find a missing dimension, requiring algebraic manipulation of these formulae. The worksheets build fluency with these various question types through repeated practise with immediate feedback from the answer sheets.

Which year groups study volume and surface area?

These worksheets specifically target Year 11 students at Key Stage 4, focusing on the Higher tier GCSE content involving spheres, pyramids, and complex composite shapes. The National Curriculum introduces basic volume concepts in Key Stage 2 with cuboids, then extends to prisms and cylinders during Key Stage 3, but the formulae for spheres and pyramids typically appear during Year 10 and 11 as part of GCSE preparation.

By Year 11, the difficulty escalates significantly from earlier years. Students encounter multi-step problems requiring them to calculate an intermediate measurement before finding the final answer, questions combining volume with ratio or percentage increase, and reverse problems where they work from surface area back to dimensions. Many teachers find that revisiting these topics in Year 11 reveals gaps in understanding from Year 10, particularly with unit conversions between cm³ and m³ or applying Pythagoras' theorem to find slant heights on pyramids and cones.

How do you calculate surface area of pyramids?

Surface area of pyramids requires calculating the base area separately from the triangular faces, then summing all surfaces. For a square-based pyramid, students find the area of the square base, then calculate the area of each of the four identical triangular faces using 1/2 × base × slant height. The slant height often requires using Pythagoras' theorem first, which creates a common error point where students confuse perpendicular height with slant height. Teachers notice this particularly when diagrams show both measurements, and students substitute the wrong value into their triangle area calculation.

Architects and structural engineers apply these calculations when designing roofs, particularly for buildings with pyramidal or conical features like church spires or modern glass pyramids. Calculating surface area determines the quantity of roofing material required, directly affecting construction costs. Solar panel installation also uses surface area calculations to determine potential energy generation from sloped roof surfaces, making these skills relevant in renewable energy contexts that students encounter in their STEM studies.

How should teachers use these volume and surface area worksheets?

The worksheets provide structured practise that moves from straightforward formula application to more complex problem-solving involving composite shapes and reverse calculations. Teachers can use initial questions to assess whether students recall formulae accurately and substitute values correctly, then identify specific misconceptions from the working shown. The answer sheets allow students to self-mark during independent work, encouraging them to locate where errors occurred in their method rather than simply checking final answers.

Many teachers deploy these resources during targeted intervention sessions with students predicted grades 4-6, where practise with exam-style questions builds confidence with the topic. The worksheets work effectively as homework following initial teaching, allowing students to consolidate new methods before the next lesson. During revision periods, students can attempt worksheets under timed conditions to replicate exam pressure, then use the answer sheets to mark their own work and create personalised lists of question types requiring further practise before their GCSE examinations.