Year 7 Transformations Worksheets
Combining Transformations
Describing Single Transformations
Describing Enlargements (A)
Describing Enlargements (B)
Describing Rotations and Reflections
Enlargement (A)
Enlargement (B)
Enlargements on Axes
Enlargements Using Column Vectors
Lines of Symmetry
Make it Symmetrical
Refelction in Horizontal and Vertical Mirror Lines
Reflection in Horizontal, Vertical and Diagonal Mirror Lines
Reflections in X and Y Axes
Rotation (A)
Rotation (B)
Rotation (C)
Rotational and Refelctive Symmetry of Polygons
Scale Factors and Centres of Enlargement (A)
Scale Factors and Centres of Enlargement (B)
Translation Trail
Translations - from Column Vectors
Translations - from Words
How Do Transformations Worksheets Develop Key Mathematical Skills?
Transformations link numerical accuracy to visual comprehension to establish strong relationships between different mathematical fields. Students learn coordinate skills through movement studies of shapes, which enables them to develop an intuitive understanding of geometric relationships. The worksheets present a systematic sequence that develops mental agility because students need to predict results before they calculate or draw them. The dual method of visualisation followed by verification creates problem-solving methods which apply to geometry as well as algebra, statistics, and physics. The development of fluent mathematicians who can easily move between different representations occurs through regular practice with multiple transformation types.
Specific learning benefits include:
• Masters coordinate plotting techniques
• Develops spatial visualisation abilities
• Strengthens geometric vocabulary usage
• Builds graph interpretation skills
• Enhances logical reasoning processes
• Improves mathematical communication
• Creates cross-curricular connections
Essential Year 7 Geometry Topics in These Transformation Worksheets
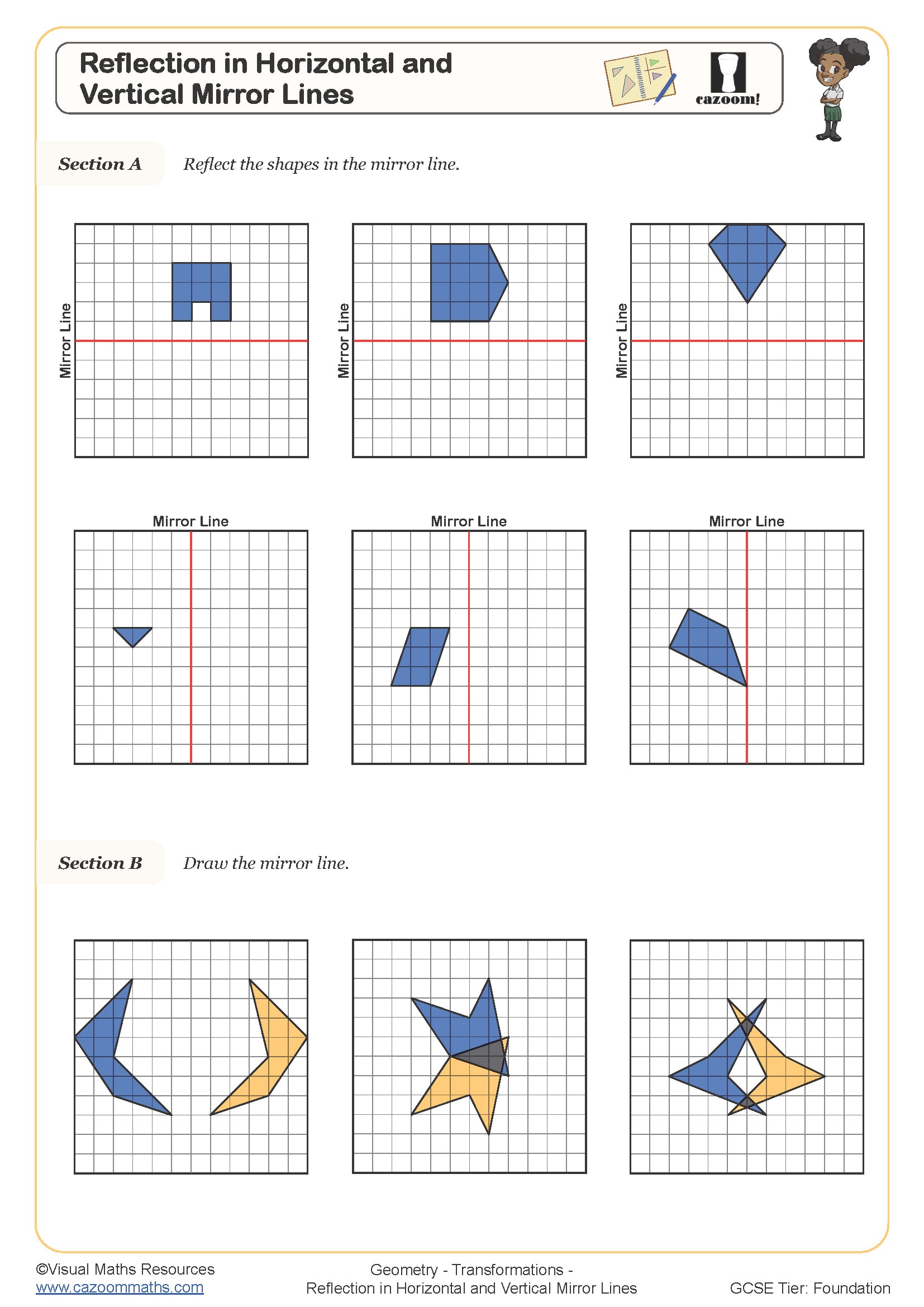
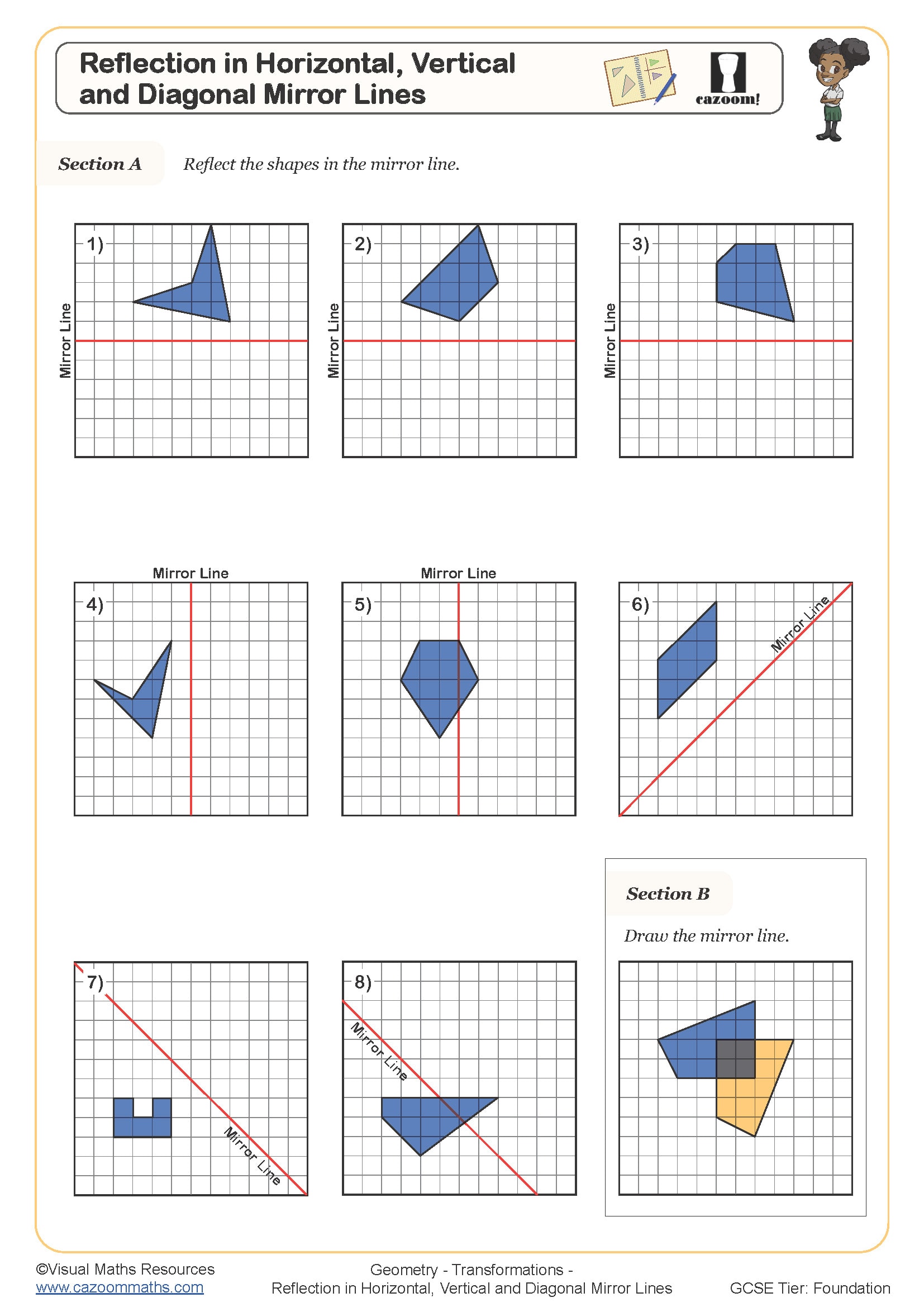
These worksheets scaffold learning from basic mirror lines through to complex combined movements, with each topic building on previous understanding. Students begin with concrete grid-based exercises before progressing to abstract coordinate notation and algebraic descriptions. The materials emphasise accuracy in both construction and description, ensuring learners can perform transformations precisely and articulate their methods clearly.
The core skills covered include:
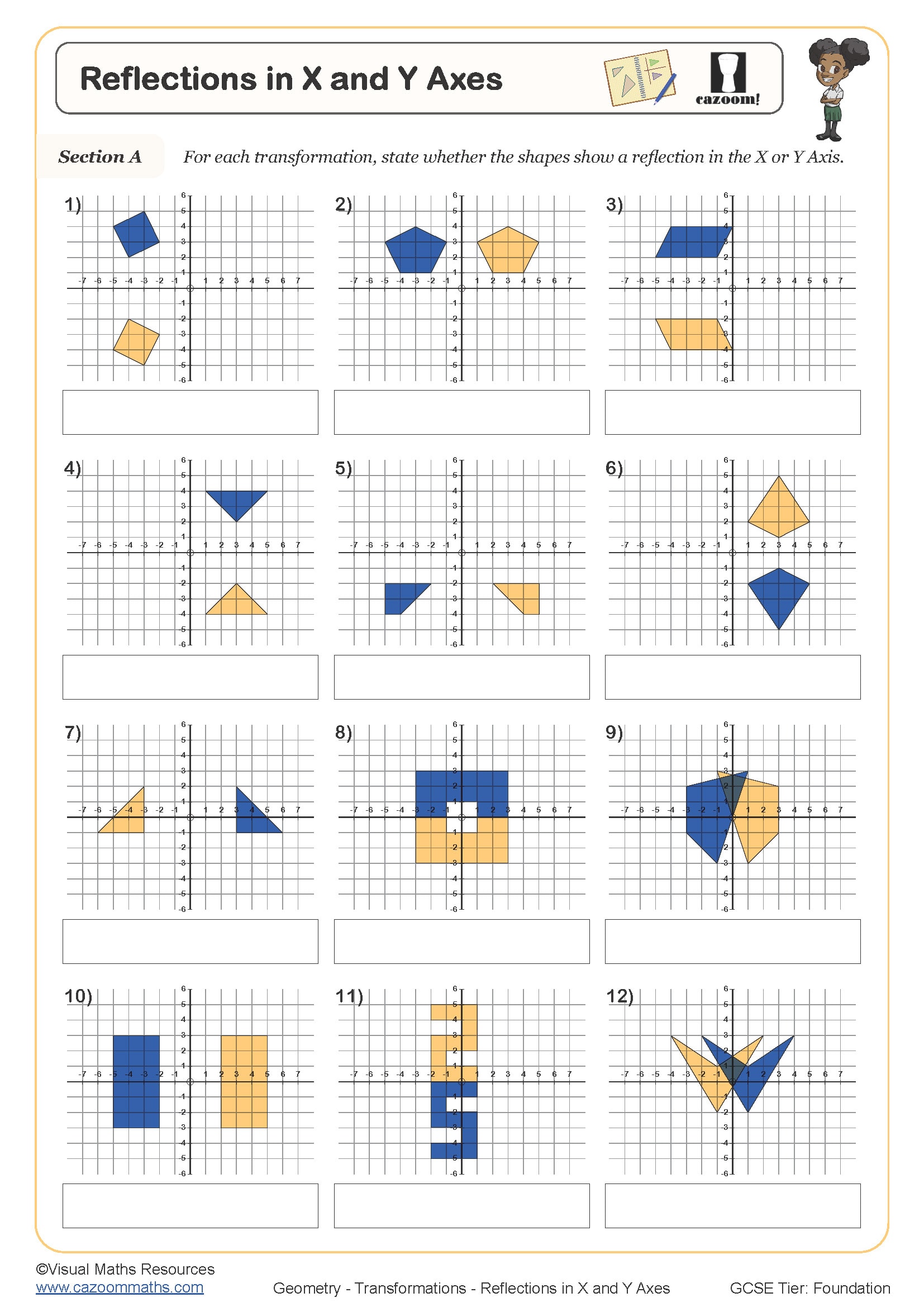
• Reflection – mirror lines on grids and axes
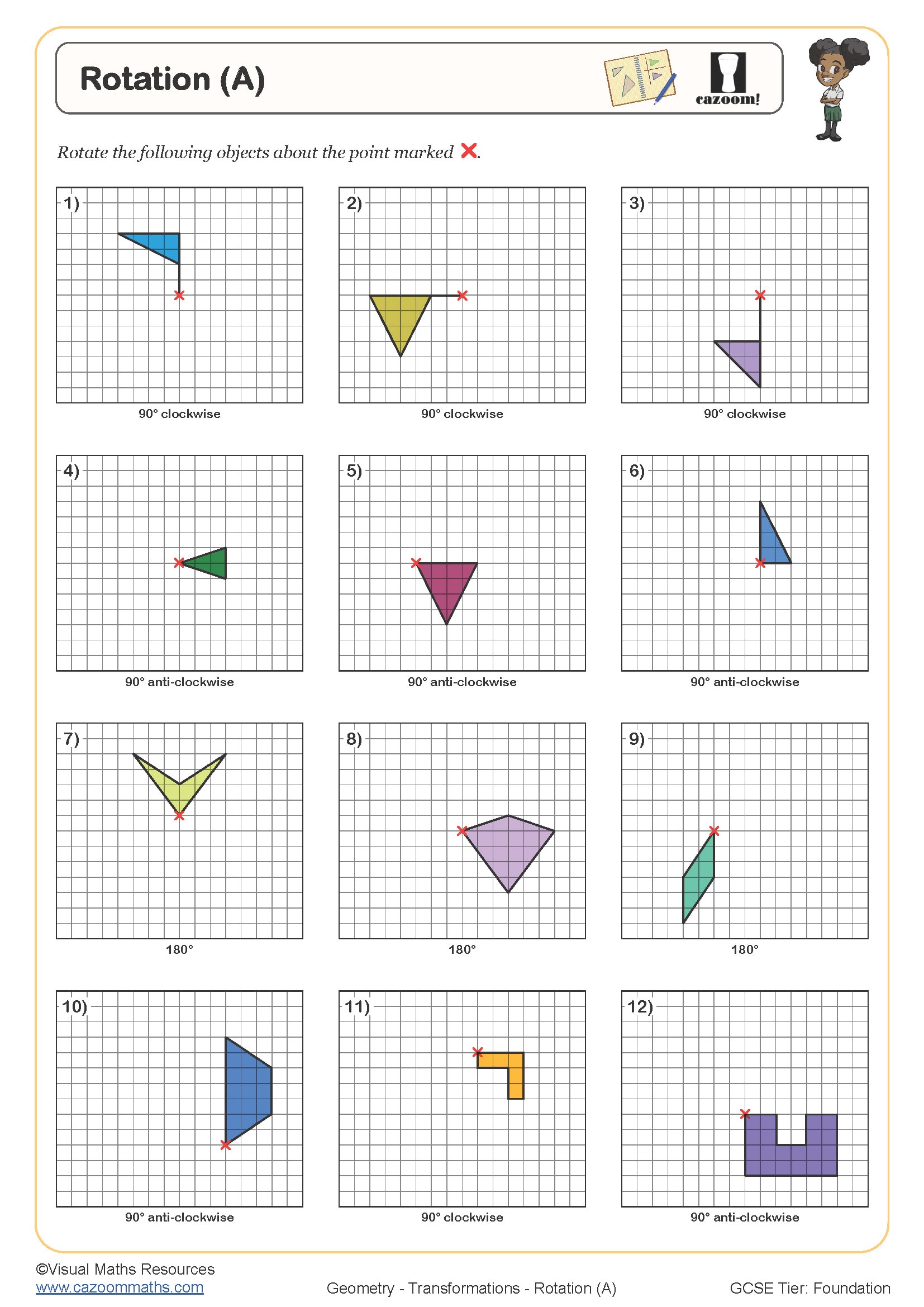
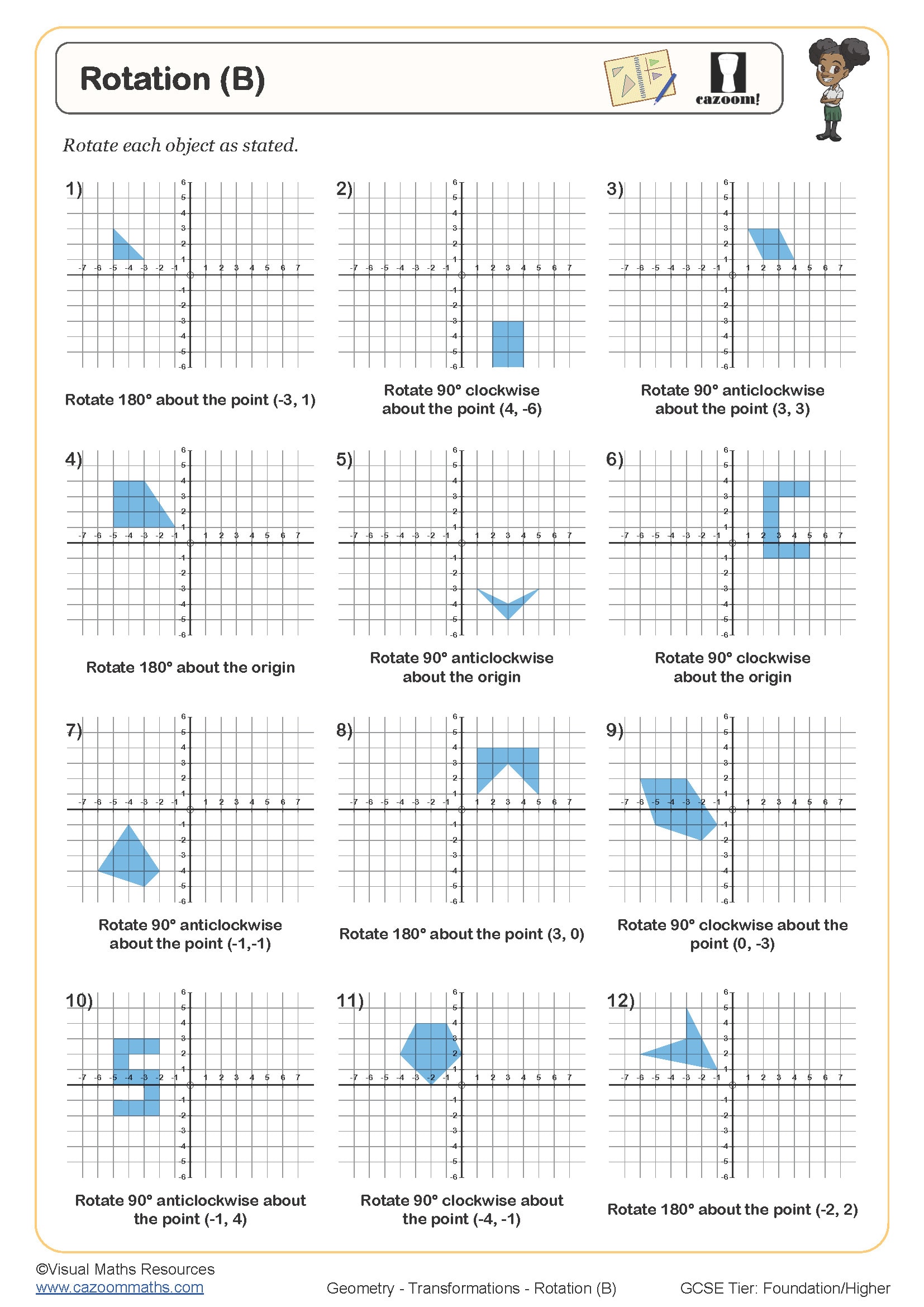
• Rotation – identifying centres, angles and direction
• Translation – vector notation and column vectors
• Enlargement – positive scale factors from given centres
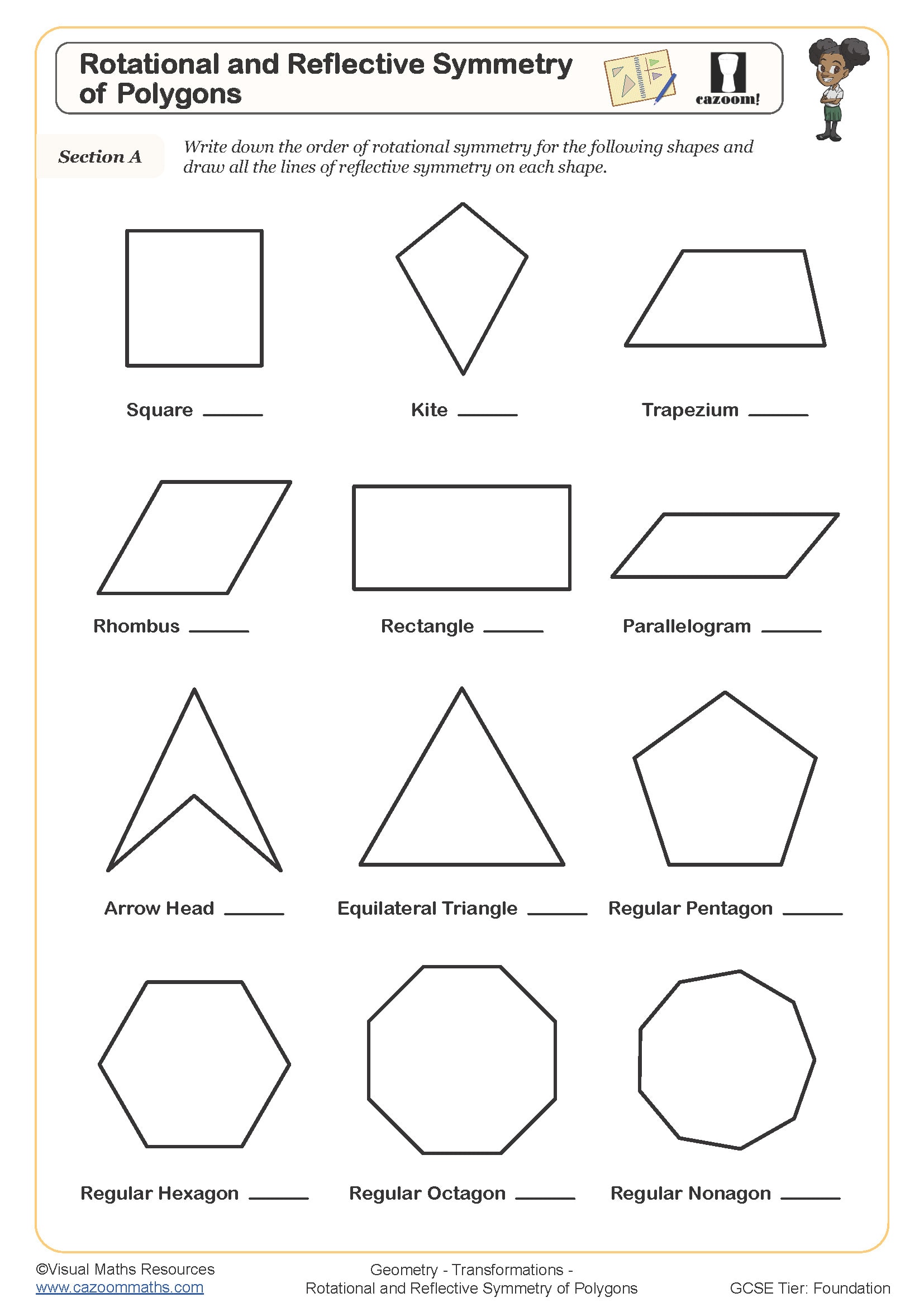
• Line symmetry – identifying and drawing symmetrical shapes
• Rotational symmetry – finding order and angles
• Combined transformations – sequencing multiple movements
• Coordinate geometry – plotting points and transformed shapes
• Describing transformations – using mathematical terminology precisely
Why KS3 Teachers Choose Cazoom Maths Transformation Resources
Real classroom experience shapes every design decision, from font clarity to question progression rates. The teachers find the material immediately ready for use because they only need to print it. The answer sheets contain complete worked solutions with step-by-step intermediate steps that enable self-marking and show typical student misunderstanding points. The visual quality remains intact during photocopying operations because it keeps all required grid lines and coordinate details. The extension questions exist as part of the lesson flow within each worksheet instead of being separate supplements. These materials function equally well for whole-class teaching, homework tasks, or targeted intervention work. The uniform format of all worksheets decreases instruction time so students can concentrate on mathematical thinking instead of learning new layouts.
Where Students Apply Transformation Knowledge in Everyday Life
Geometric transformations appear throughout technology, design and nature, making these skills immediately relevant.
Real-world applications include:
• Video game design – programming character movements and animations
• Architecture – creating symmetrical building facades
• Textile patterns – designing repeating motifs for fabrics
• Engineering drawings – showing different object views
• Logo design – developing balanced brand imagery
• Dance choreography – planning formation changes
• Navigation apps – rotating maps to match direction
• 3D printing – understanding object orientation and scaling