Year 8 Area Model Worksheets
Expanding Brackets and Simplifying - Using Algebra Tiles

Expanding Double Brackets (A) Using the Grid Method

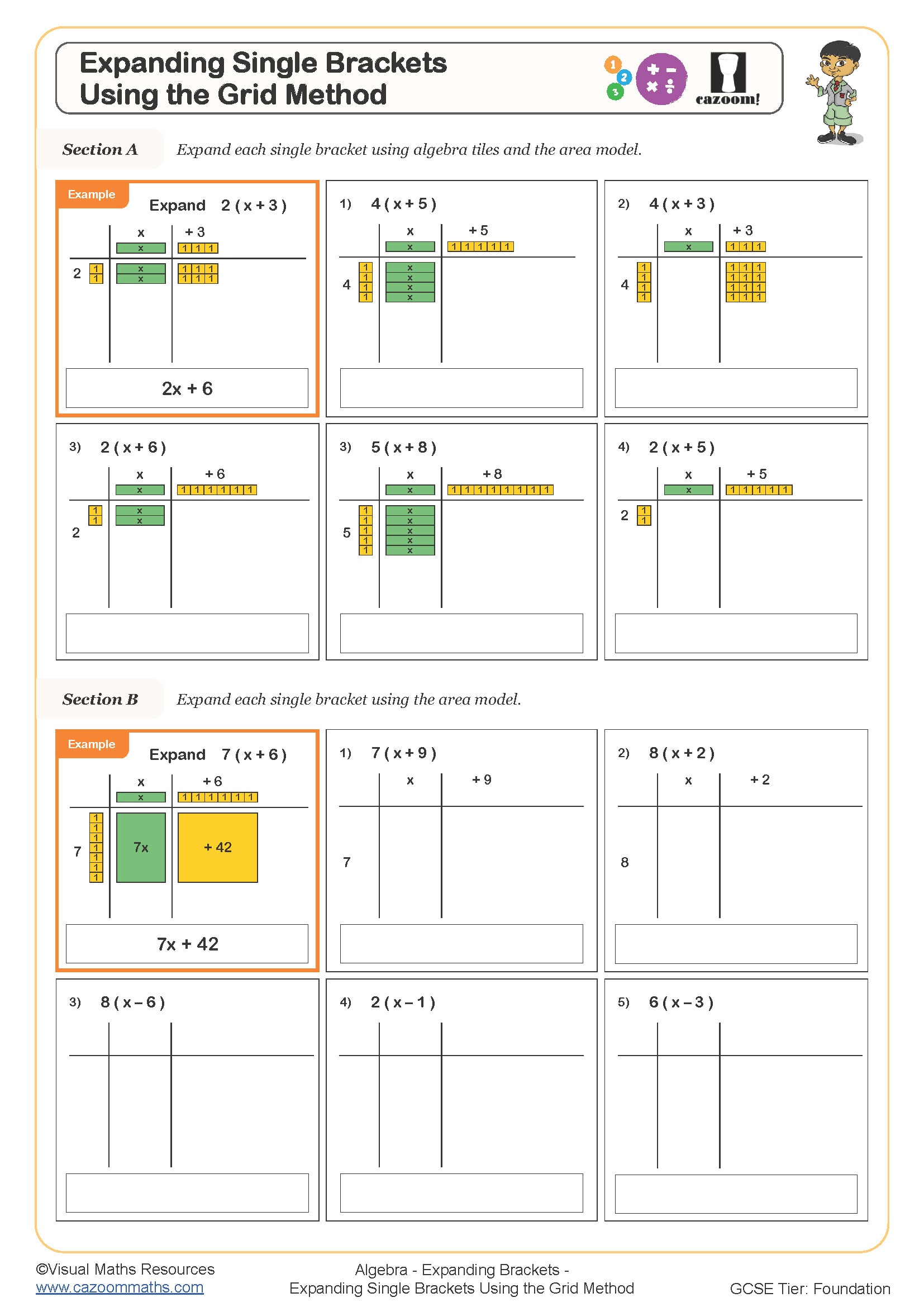
Expanding Single Brackets - Using the Grid Method
Factorising Using the Area Model

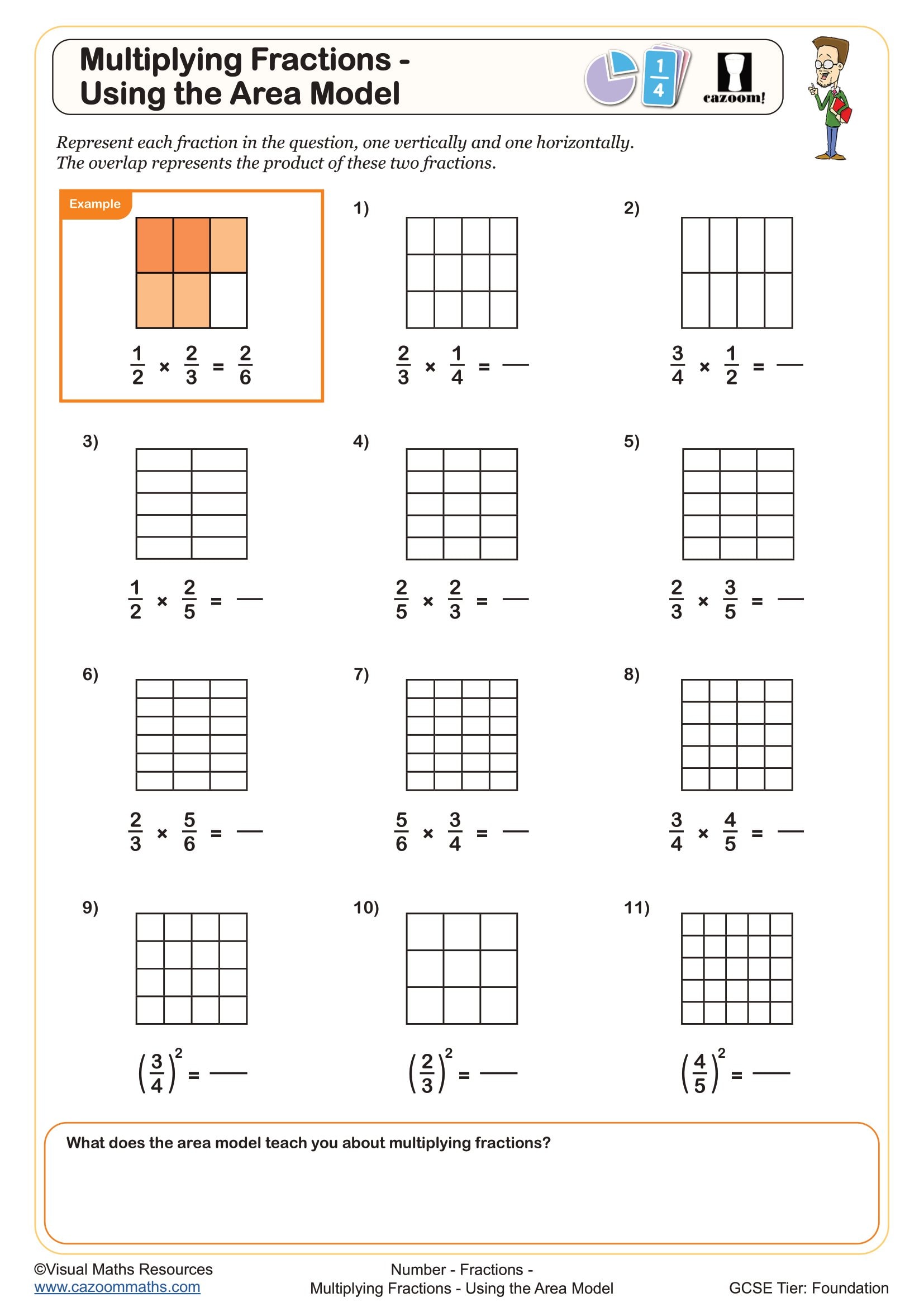
Multiplying Fractions - Using the Area Model
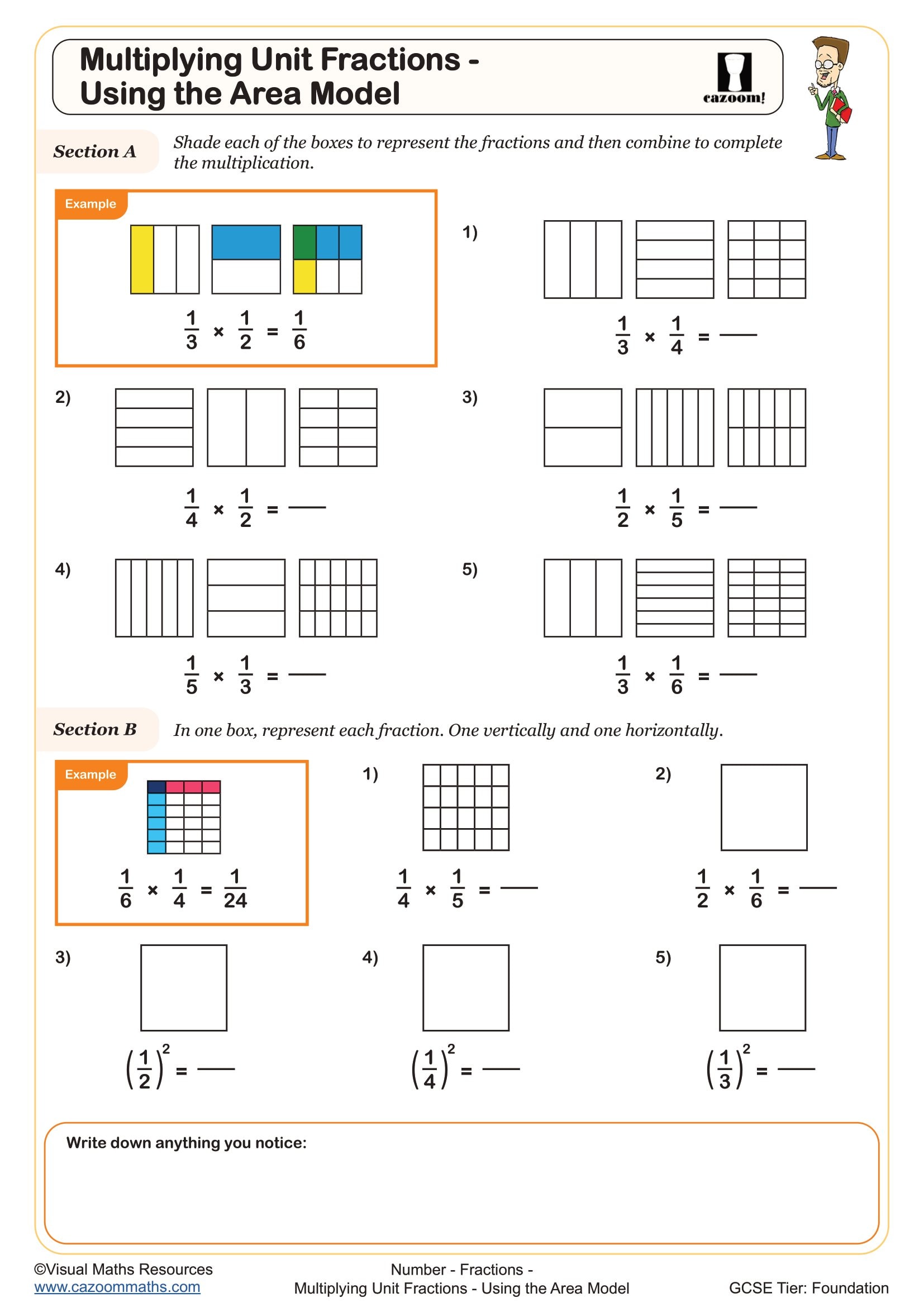
Multiplying Unit Fractions - Using the Area Model
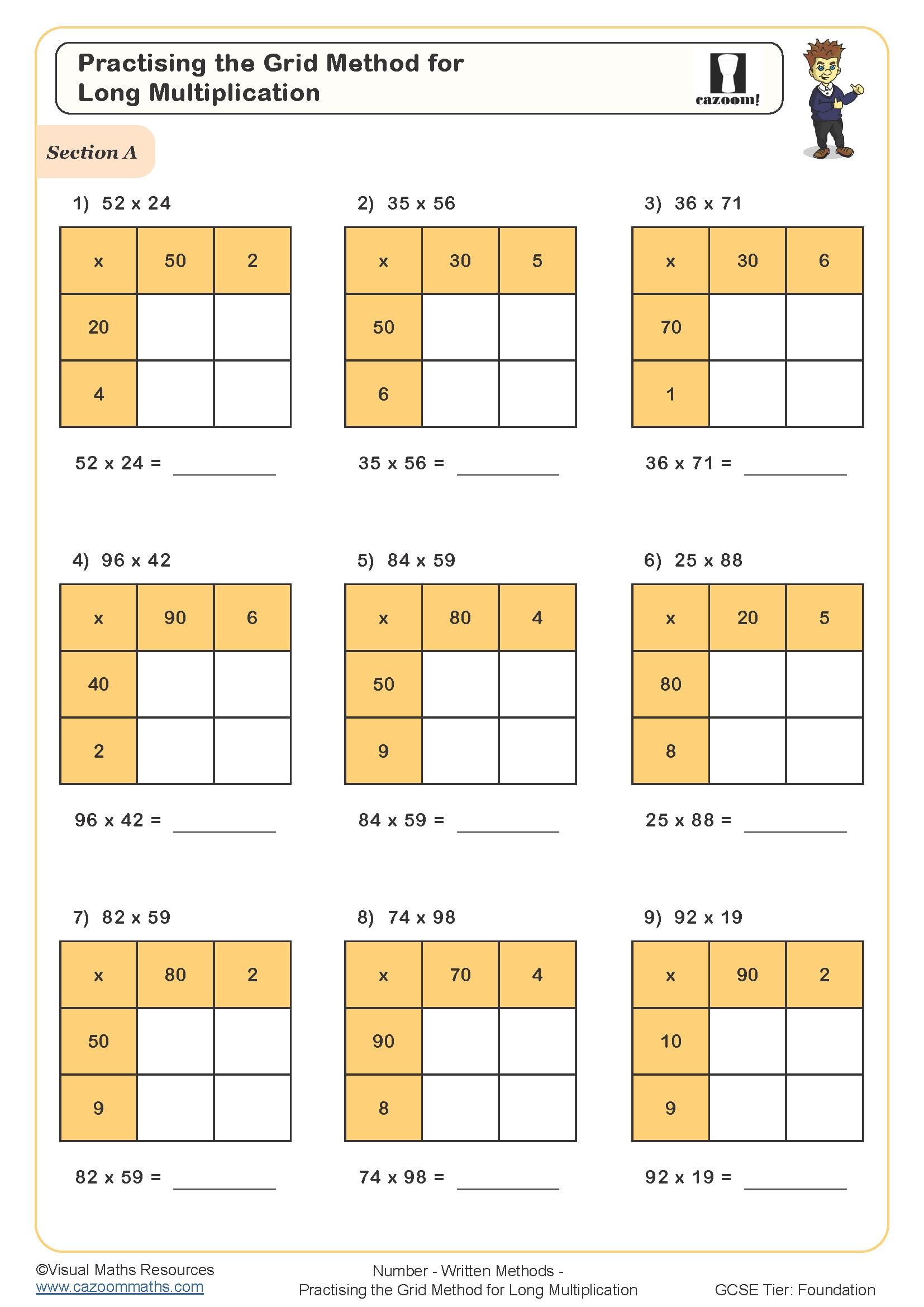
Practising the Grid Method for Long Multiplication
Practising the Grid Method for Short Multiplication (A)
All worksheets are created by the team of experienced teachers at Cazoom Maths.
What are area model worksheets used for in Year 8 maths?
Area model worksheets provide a visual method for multiplication, expansion, and factorisation by representing calculations as rectangles divided into sections. In Year 8, students use this approach to multiply larger numbers without calculators, expand single and double brackets, and begin factorising quadratic expressions. The model reinforces the distributive property and helps students understand why algebraic processes work rather than just memorising procedures.
Teachers frequently notice that students forget to multiply every term when expanding brackets like (x + 3)(x + 5), commonly producing x² + 15 instead of x² + 8x + 15. The area model prevents this error because the rectangular grid shows four distinct sections that must each be calculated. Students can physically see which terms they've addressed and which remain, making it harder to skip the middle terms that often disappear in purely symbolic work.
Which year groups use area models in the UK curriculum?
Area models appear primarily in Year 8 as part of the Key Stage 3 programme of study, where students develop confidence with algebraic notation and manipulation. The National Curriculum expects students to understand the relationship between geometric representations and algebraic expressions during this stage. Whilst the visual approach originates in primary multiplication strategies, its application to algebra typically begins when students encounter bracket expansion systematically.
The complexity increases throughout Year 8, starting with multiplying two-digit numbers to reinforce place value understanding before progressing to algebraic terms. Early worksheets focus on single bracket expansion like 3(2x + 5), then advance to double brackets (x + 4)(x + 7), and finally introduce factorising quadratic expressions by working backwards through the model. This scaffolded approach builds procedural fluency alongside conceptual understanding, preparing students for GCSE algebraic manipulation where area models become a problem-solving tool rather than the primary method.
How does the area model connect to factorising quadratic expressions?
The area model for factorising requires students to work backwards from a completed rectangle to find the dimensions that created it. Given an expression like x² + 7x + 12, students construct a rectangle with area x² in one corner and constant 12 in the opposite corner, then determine which terms along the sides produce the middle term 7x when multiplied. This reverses the expansion process and makes factorising feel like solving a puzzle rather than guessing factor pairs.
This spatial reasoning appears throughout design and engineering contexts where professionals work backwards from specifications to required dimensions. Architects determining room dimensions from area requirements, packaging designers calculating box measurements from volume constraints, and engineers sizing components from load specifications all apply this reverse-calculation thinking. The area model teaches students that algebraic factorising represents finding unknown lengths when you know the resulting area, a concept they'll encounter repeatedly in GCSE problem-solving questions involving geometric contexts.
How can teachers use these area model worksheets effectively?
The worksheets build systematically from numerical examples that reinforce place value through to increasingly complex algebraic applications, allowing teachers to identify precisely where understanding breaks down. Each sheet includes worked examples showing how to label the rectangle's dimensions, partition it correctly, calculate each section's area, and combine like terms. The answer sheets show complete working for every question, which helps students self-diagnose errors in their process rather than just checking final answers.
Teachers report these worksheets work particularly well for intervention with students who struggle with abstract algebraic manipulation, as the visual representation provides an alternative entry point to the same mathematics. They're effective as homework following initial teaching because the consistent structure reduces cognitive load around instructions, letting students focus on the mathematical thinking. Many teachers use them for paired work where students compare their rectangle constructions, as discussing why terms appear in specific positions deepens understanding of the distributive property more effectively than individual practice alone.