Year 9 Algebra Tiles Worksheets
What are algebra tiles and how do they help students learn algebra?
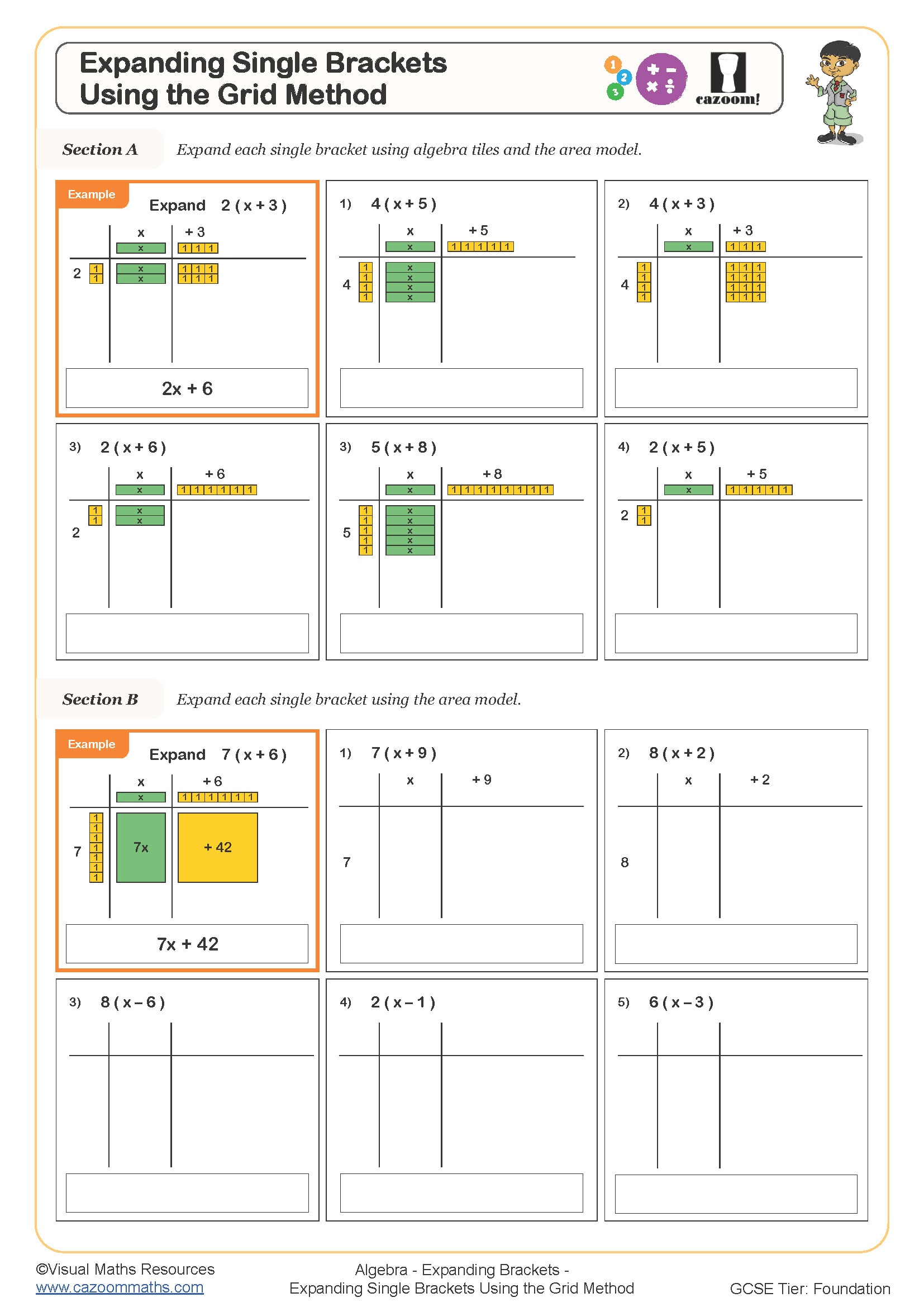
Algebra tiles are manipulatives that represent algebraic terms visually: typically, large squares represent x², rectangles represent x, and small squares represent unit values (constants). They allow students to build, combine, and simplify expressions by physically arranging tiles, making the abstract rules of algebra more concrete and logical.
Many teachers find that students who memorise algebra rules without understanding often make errors when combining unlike terms or dealing with negative values. Using algebra tiles, students can see why x + x becomes 2x (two rectangles placed together) but why x + 1 cannot be simplified (different tile shapes). This visual foundation helps prevent the common mistake of adding x + 3 to get '4x', because students recognise they're working with fundamentally different quantities.
Which year groups use algebra tiles in the UK curriculum?
Algebra tiles are primarily introduced during Year 9 as part of the KS3 programme of study, though some schools begin exploration in Year 8 depending on student readiness. At this stage, the National Curriculum expects students to manipulate algebraic expressions fluently, and tiles provide scaffolding for those who find symbolic manipulation challenging.
Whilst younger students might encounter basic tile work when first meeting simple expressions, Year 9 represents the point where tiles support more sophisticated algebra including simplification of complex expressions, working with negative terms, and solving equations with unknowns on both sides. Teachers typically phase out tile dependency as students develop confidence with symbolic methods, using them strategically for intervention or when introducing particularly challenging new concepts like factorising quadratics.
How do algebra tiles help with solving equations with unknowns on both sides?
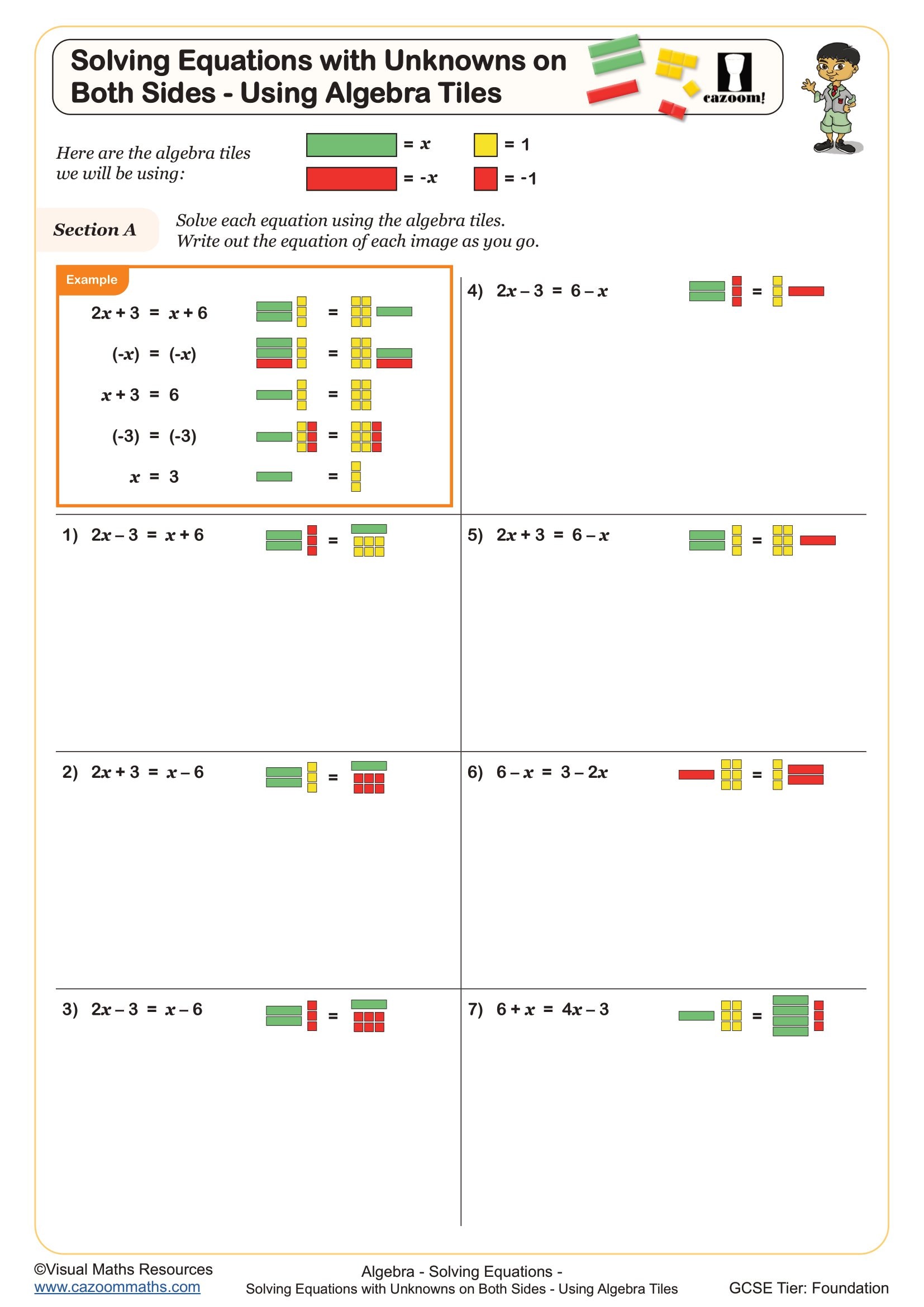
When solving equations like 3x + 2 = x + 8, students can model both sides using tiles and then apply the principle of 'balancing' by removing or adding identical tiles to both sides. They physically remove one x-tile from each side, then remove two unit tiles from each side, making the abstract process of 'doing the same to both sides' completely visible and logical.
This skill connects directly to engineering and computer science contexts where balancing equations appears constantly. Engineers use similar principles when calculating forces in equilibrium, where quantities on each side of an equals sign must match. In programming, understanding that expressions on either side of an assignment or comparison operator must balance helps students grasp conditional logic and variable manipulation, making algebra tiles a foundation for computational thinking as well as pure mathematics.
How should teachers use algebra tiles worksheets in the classroom?
The worksheets work most effectively when students have physical or virtual algebra tiles available alongside the written exercises, allowing them to model each problem before recording their answer symbolically. Teachers can use the scaffolded approach within each worksheet to gradually reduce tile dependency, starting with diagrams provided and progressing to students choosing whether to use tiles themselves.
These resources suit various classroom scenarios: small group intervention for students who struggle with abstract algebra, paired work where one student models with tiles whilst their partner writes symbolically, or homework where students sketch tile representations before solving. The complete answer sheets allow students to self-check their understanding, particularly useful for independent revision before assessments or for teachers running differentiated stations where students move through activities at their own pace.