Year 9 Area Model Worksheets
All worksheets are created by the team of experienced teachers at Cazoom Maths.
What is the area model in maths?
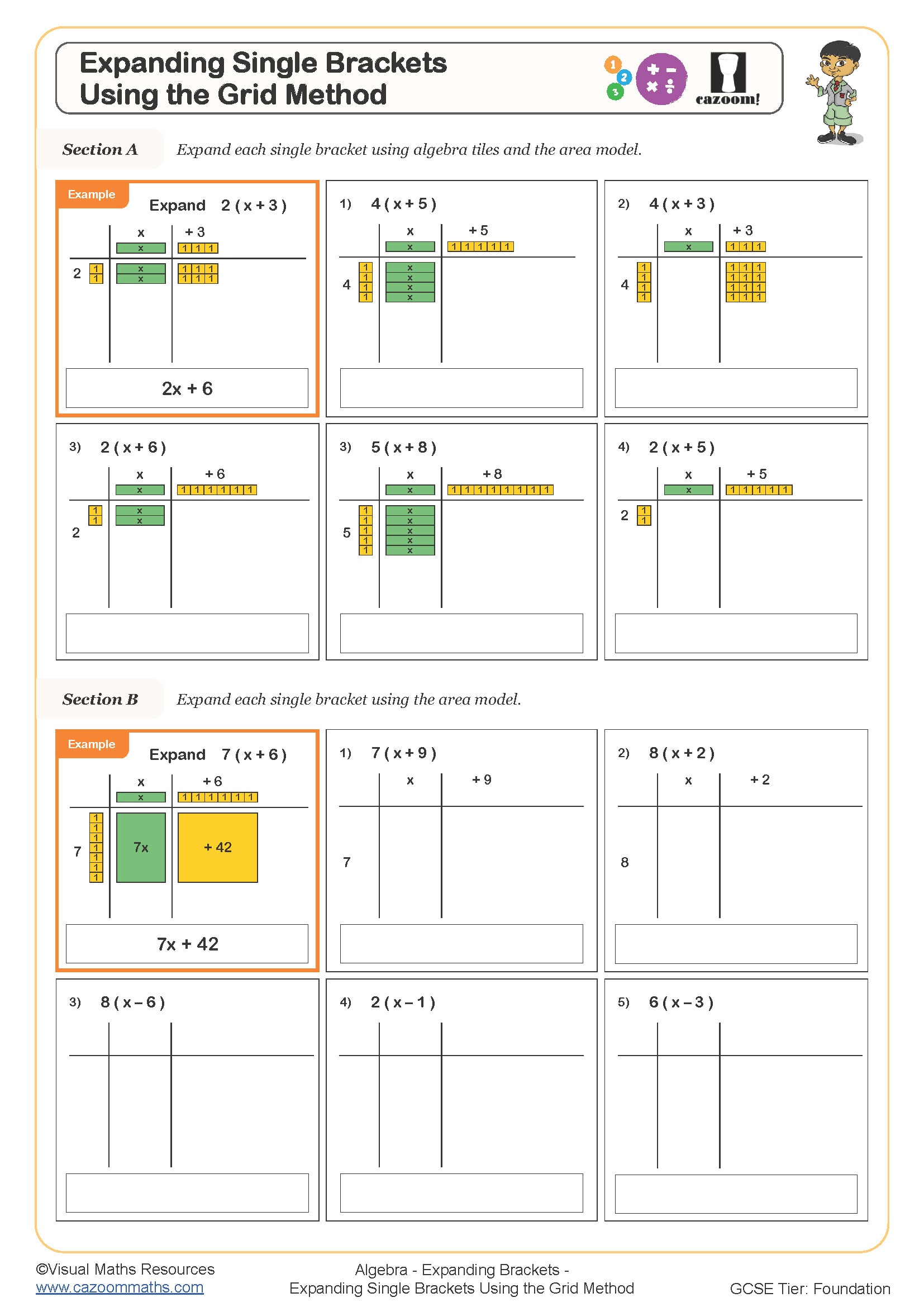
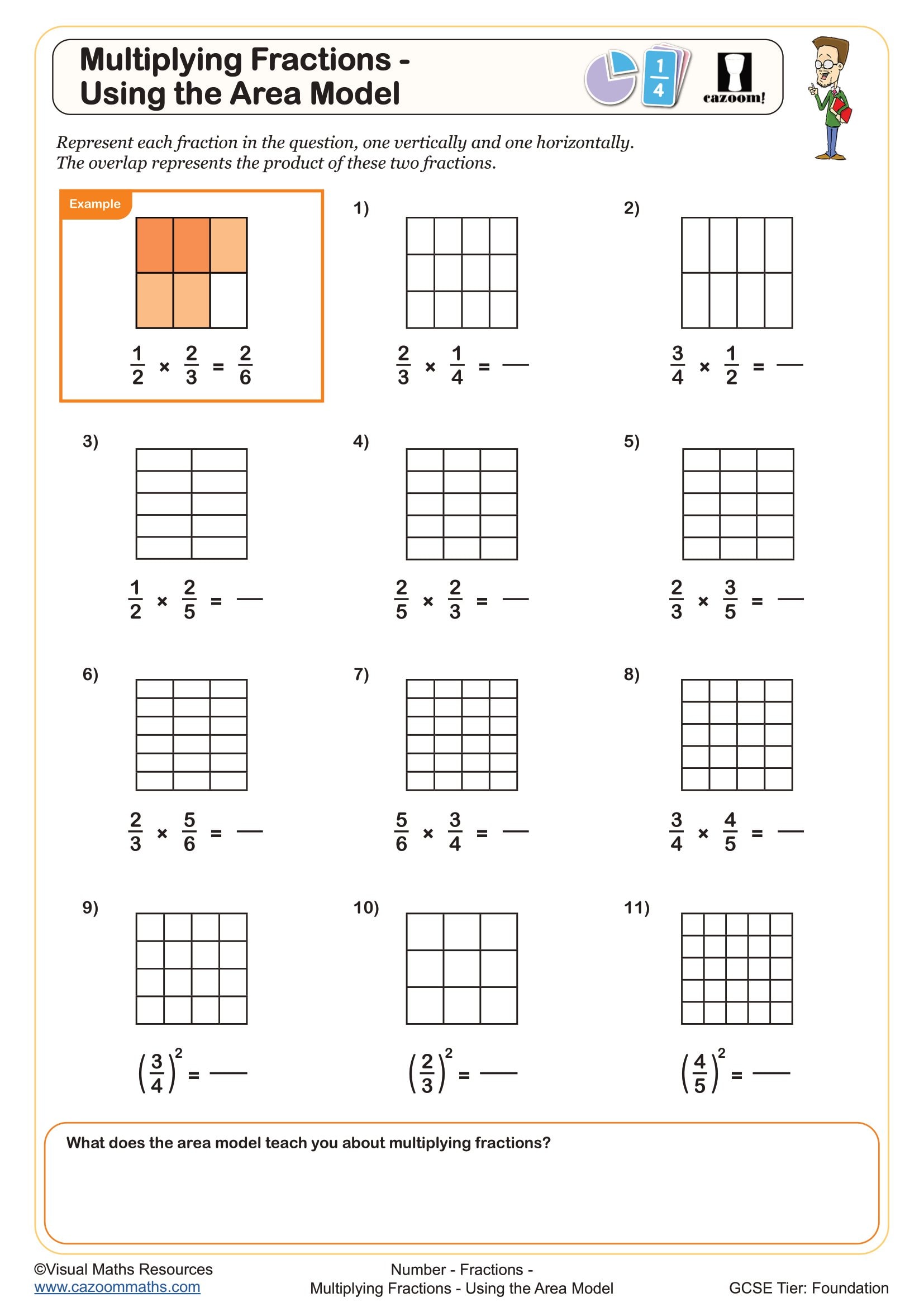
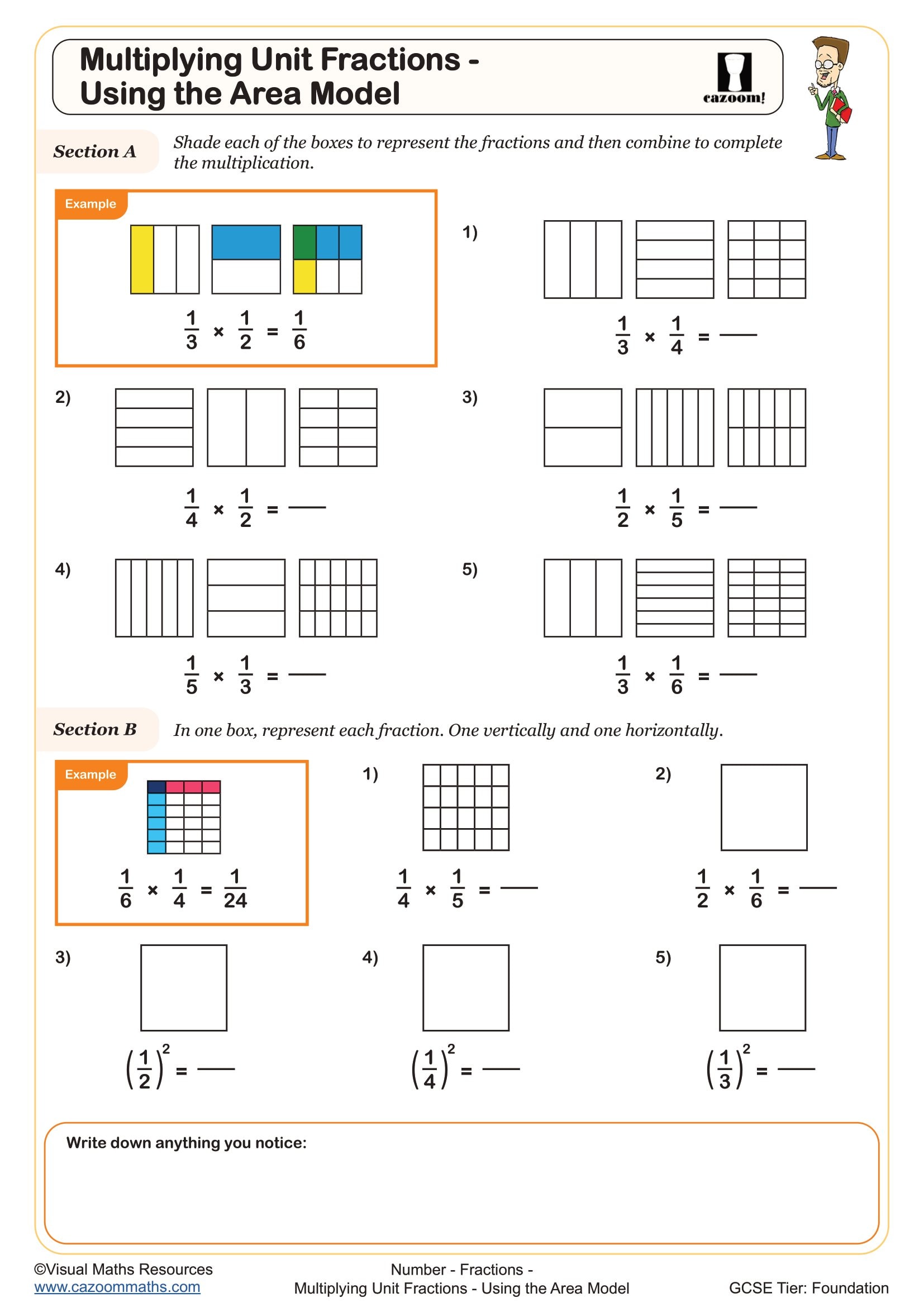
The area model is a visual method for multiplication that represents calculations as rectangles divided into sections. Students partition numbers or expressions along the sides of a rectangle, then find the area of each section before combining them. This technique works for both numerical multiplication and algebraic expansion, making it particularly valuable when students move from arithmetic to algebra at Key Stage 3.
In the classroom, the area model helps students understand why (x + 3)(x + 5) equals x² + 8x + 15 rather than just memorising FOIL. Teachers observe that students who use area models make fewer sign errors when expanding brackets because they can see each product separately. The method also supports factorising, as students work backwards from the rectangular sections to identify the original expressions along the sides.
Which year group learns area model methods?
These worksheets target Year 9 students in Key Stage 3, when algebraic manipulation becomes more sophisticated and students need reliable methods for expanding and factorising expressions. The area model bridges the gap between numerical understanding and abstract algebra, appearing in schemes of work as students encounter quadratic expressions for the first time. At this stage, students apply the method to expressions involving brackets, building towards GCSE content on quadratic equations.
Whilst some students may encounter area models for numerical multiplication earlier, Year 9 focuses on algebraic applications. The progression involves starting with simpler expressions like (x + 2)(x + 4), then advancing to cases with negatives such as (x - 3)(x + 7), and eventually expressions with coefficients like (2x + 5)(3x - 1). This structured approach ensures students develop fluency before tackling GCSE-level problems independently.
How does the area model help with expanding brackets?
The area model transforms bracket expansion from an abstract process into a geometric calculation. Students draw a rectangle, write the terms from the first bracket along one side and terms from the second bracket along another, then calculate the area of each section formed by the grid. This visual representation ensures every term gets multiplied correctly, reducing the errors that occur when students try to expand mentally or rush through algebraic steps.
This method connects directly to real-world applications in engineering and design. When architects calculate floor areas for irregularly shaped rooms, they often partition the space into rectangles, find individual areas, then sum them—exactly the process students practise with algebraic expressions. Understanding that (length₁ + length₂)(width₁ + width₂) gives total area helps students see why algebraic expansion works the way it does, strengthening their spatial reasoning alongside algebraic fluency.
How should teachers use area model worksheets in lessons?
The worksheets provide structured practise that moves from basic algebraic expansions to more challenging problems involving negative terms and larger coefficients. Starting with guided examples helps students understand the grid structure before attempting independent questions. Teachers can model the first problem on the board, emphasising how to position terms correctly and combine like terms systematically, then have students complete similar questions with the scaffolding still visible.
Many teachers use these worksheets during intervention sessions for students who struggle with traditional FOIL methods, as the visual approach often clicks where verbal explanations haven't. The resources work well for homework consolidation after introducing the technique, or as starters to maintain fluency over several weeks. Paired work allows students to compare their grids and discuss discrepancies before checking against the answer sheets, developing their error-analysis skills alongside algebraic understanding.