Year 9 Circle Worksheets
Area and Circumference
Area of Circles
Area of Sectors and Arc Lengths
Area of Sectors and Segments
Area of Sectors and Segments (With Clues)
Circle Area Problems
Circle Investigation - Discovering Pi
Circle Theorems (A)
Circle Theorems (B)
Circle Theorems (C)
Circle Theorems: Angle at Center Twice the Angle at Circumference
Circle Theorems: Angle Notation
Circle Theorems: Cyclic Quadrilaterals
Circle Theorems: Triangles in Circles
Circumference
Finding the Radius or Diameter from the Circumference and Area
In Terms of Pi (A)
In Terms of Pi (B)
In Terms of Pi (C)
In Terms of Pi (D)
Introducing Radians
Learning the Circle Theorems
Parts of a Circle
Proving Circle Theorems
Proving Circle Theorems - Angle at the Centre
Proving Circle Theorems - Angle in a Semicircle
Proving Circle Theorems - Angles in the Same Segment
Proving Circle Theorems - Cyclic Quadrilaterals
The Formulae for Area of Sectors and Arc Lengths
The Benefits of Using Year 9 Circle Worksheets Every Week
Students consolidate their prior knowledge of perimeter and angles, then extend it to circle measures and theorem-based reasoning. The process of careful sequencing, which includes formula selection and substitution, rearrangement, and interpretation, helps prevent errors that occur when people mix radius and diameter measurements or when they round numbers prematurely. Students learn to express answers in terms of π through regular practice between using exact values and calculator operations. The practice material presents different types of problems in a regular pattern, which makes the methods applicable for solving problems both with and without a calculator. Students learn to solve new problems and complex tasks that involve sector and arc calculations, as well as theorem applications, as their comprehension advances. The following section contains a summary of all the benefits you will get.
Specific learning benefits include:
• Develops fluency with πr², 2πr and πd
• Strengthens rearrangement to find missing radii or diameters
• Builds confidence using exact answers in terms of π
• Improves unit awareness and reliable rounding decisions
• Extends reasoning into sectors, arcs, and angle theorems
• Prepares pupils for end-of-year assessments at KS3
What Our KS3 Geometry Worksheets Cover: Skills, Methods, and Titles
The collection moves from concrete and pictorial prompts (labelling parts, shading sectors, tracing arcs) to abstract, exam-style questions. Guided examples transition into independent practice, with worked solutions included, allowing learners to follow each line of reasoning and self-check. A balance of exact and decimal answers ensures students know when to simplify and when to approximate.
The worksheets in this collection include:
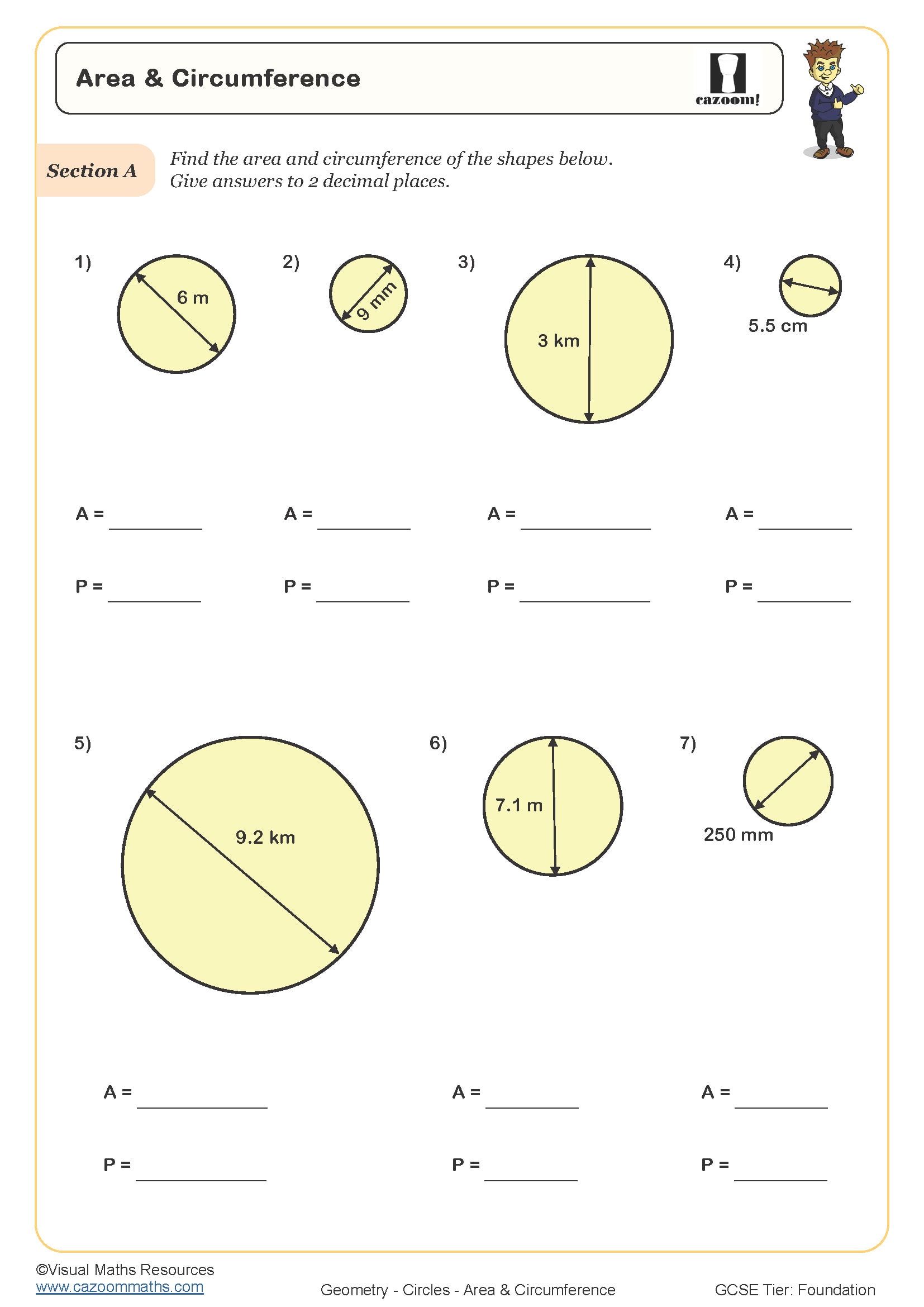
• Area and Circumference — calculate circle area and perimeter from radius/diameter.
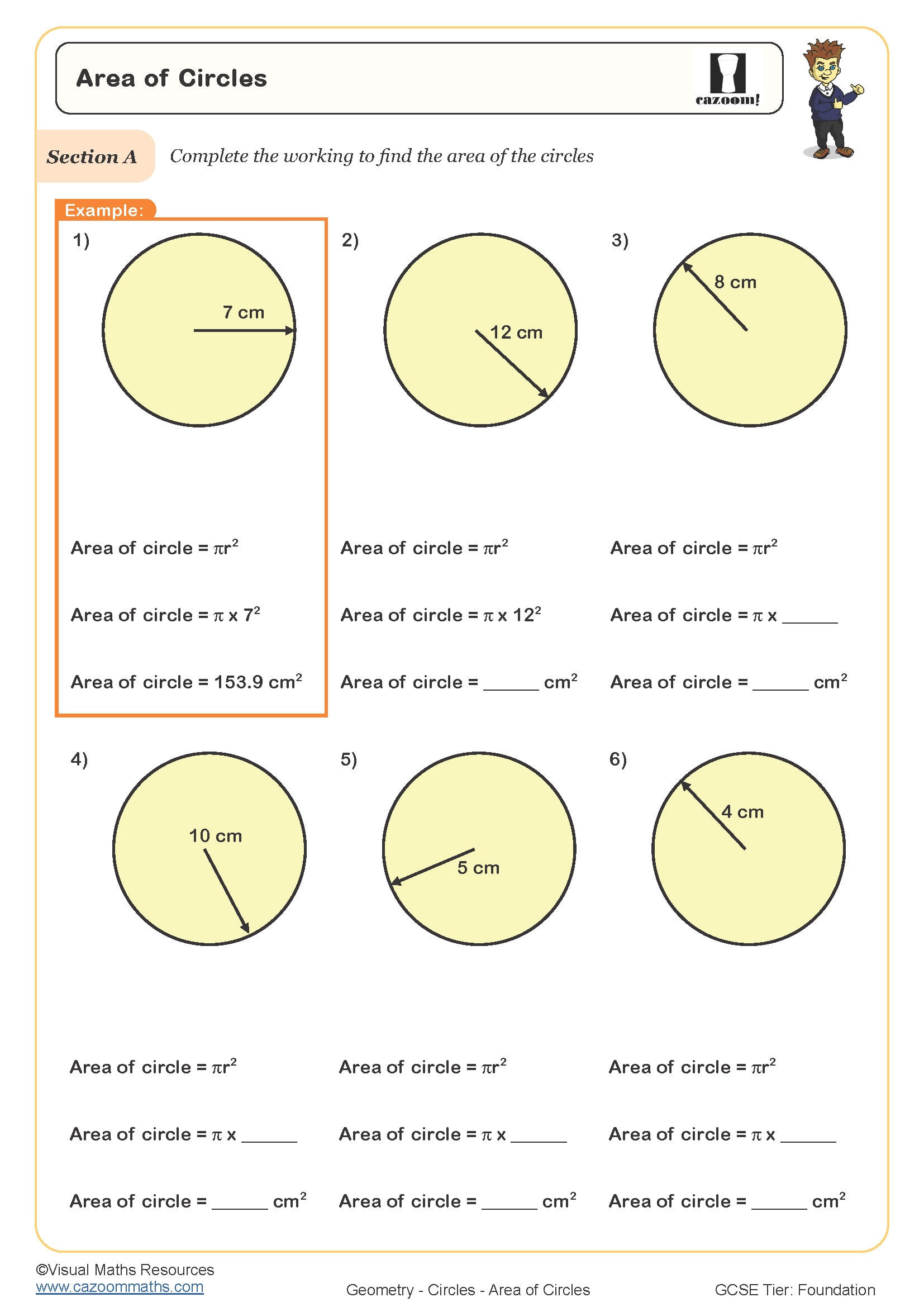
• Area of Circles — practise using πr², convert between radius and diameter.
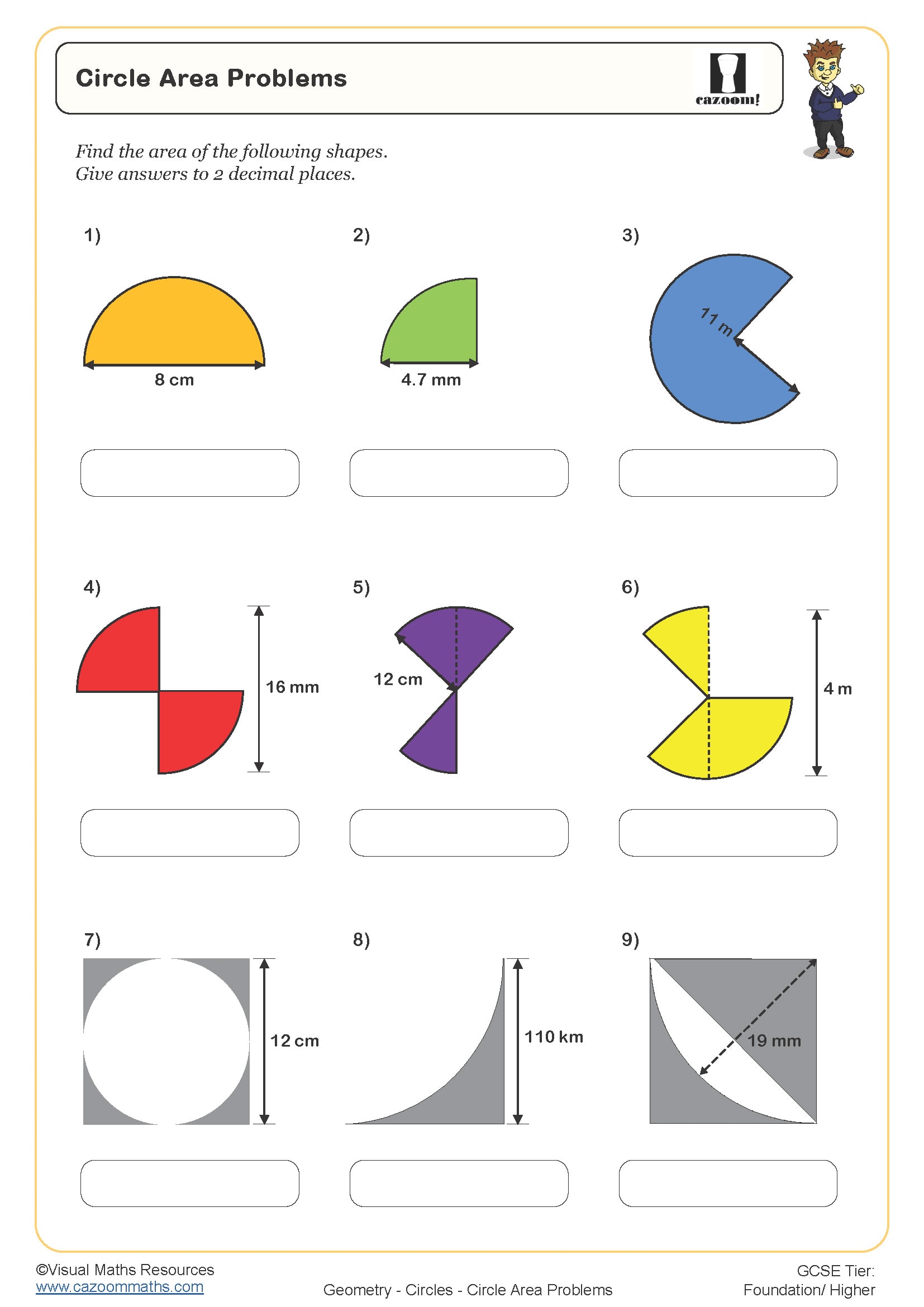
• Circle Area Problems — solve multi-step contexts requiring area calculations and units.
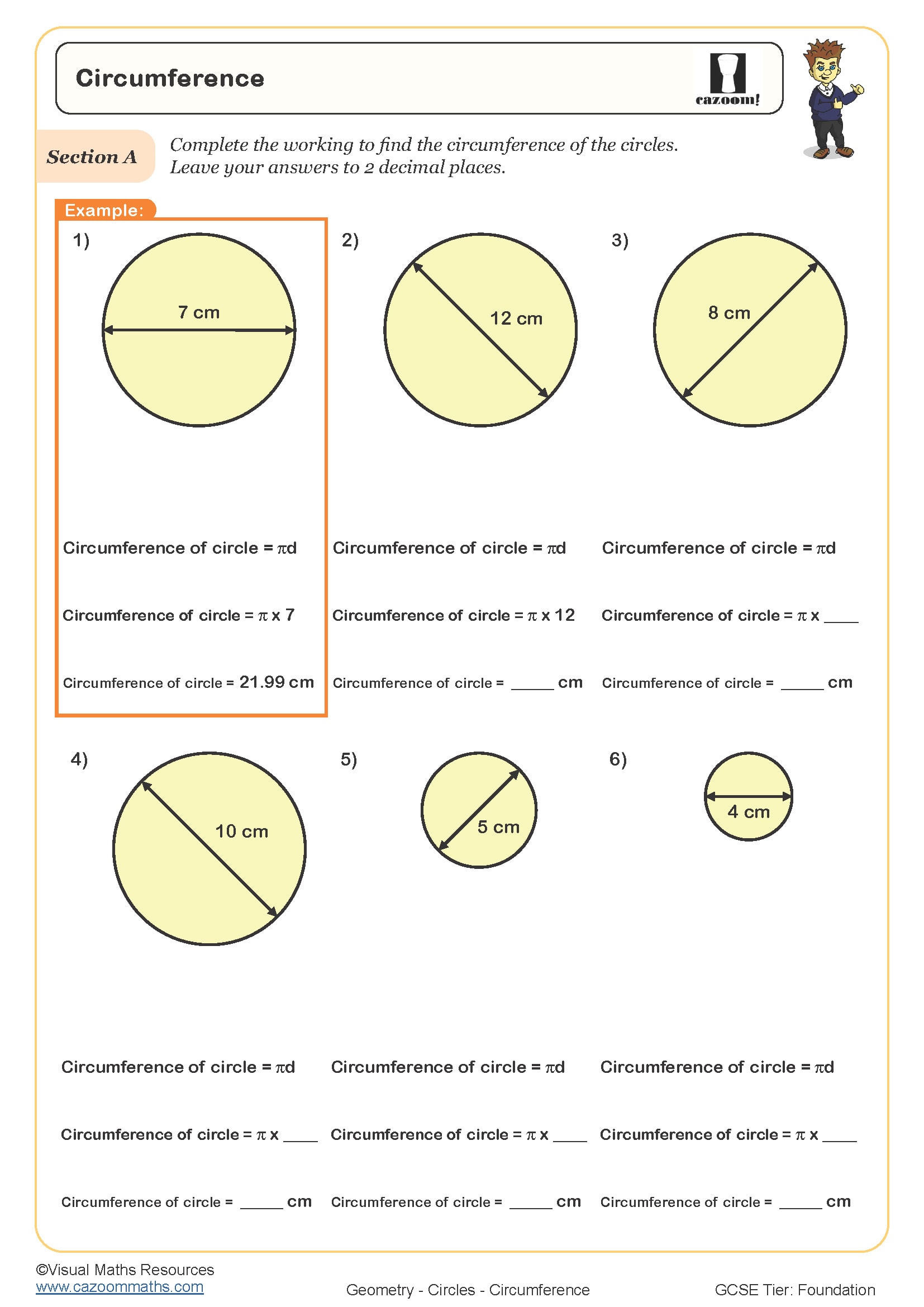
• Circumference — work with 2πr or πd to find perimeters precisely.
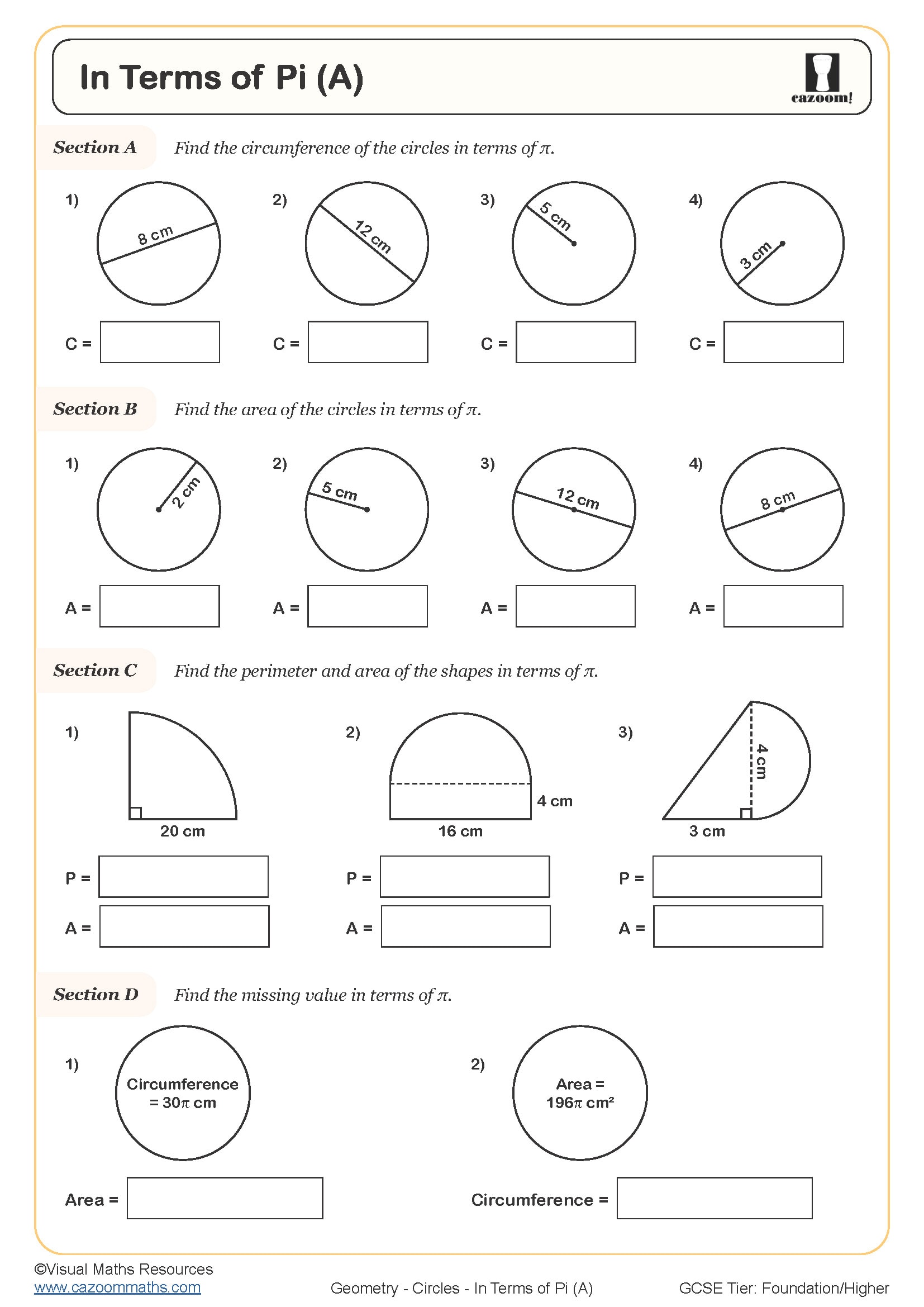
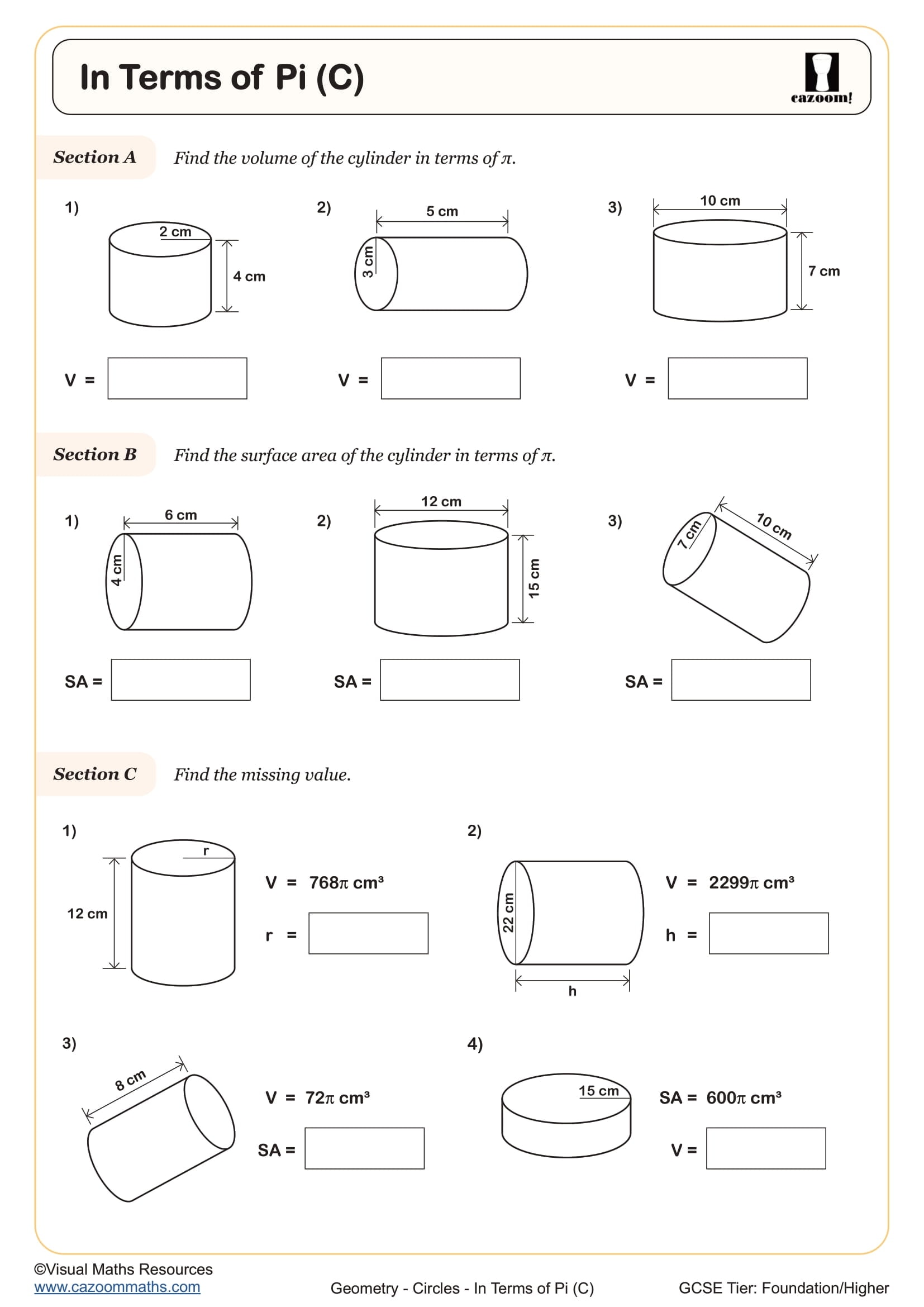
• In Terms of Pi — leave exact values; simplify factors of π correctly.
• Parts of a Circle — identify centre, radius, diameter, chord, tangent, sector.
• Area of Sectors and Arc Lengths — find fractional areas and curved lengths of sectors.
• Circle Theorems: Angle at Centre Twice the Angle at Circumference — prove and apply the central theorem with examples.
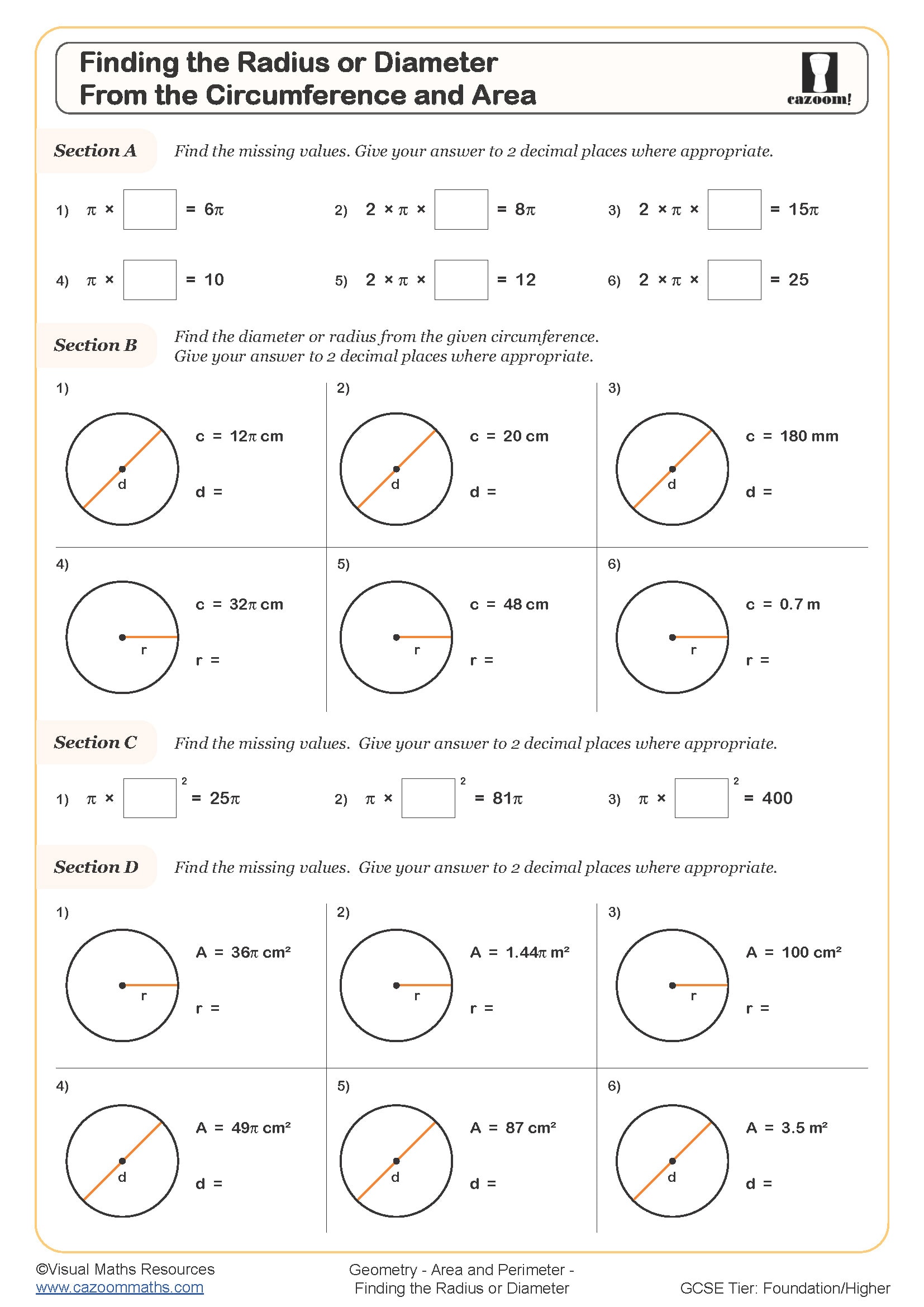
• Finding the Radius or Diameter from the Circumference and Area — rearrange formulae to determine missing measures confidently.
• The Formulae for Area of Sectors and Arc Lengths — recall, manipulate and apply both sector formulae.
How Teachers Use Year 9 Circle Worksheets to Save Planning Time
Every page is classroom-ready: clean layouts, short sets that fit a lesson, and a logical ramp in difficulty for mixed-attainment groups. The approach of explicit modelling helps teachers reduce their speaking time, yet different entry points in the tasks maintain student accessibility at the same level of mathematical complexity. Extension prompts and exact-value options function to enhance the challenge for students who learn concepts quickly. The full method appears on time-saving answer sheets, which enable you to show students both their mistakes and the correct, efficient solution steps. The consistent framework of Cazoom Maths provides dependable progress through quick starts, smooth marking and retrieval starters and focused practice and homework and targeted intervention. The platform offers reliable solutions that you can rely on.
Everyday Maths: Where Year 9 Students Use Circle Skills in Real Life
Circle measures and theorems underpin everyday design, planning, and measurement, from quick estimates to precise specifications.
• Choosing bicycle tyre sizes and checking rim circumferences
• The evaluation of pizza size serves as a method to determine the price-quality ratio of different pizza options.
• The design of gardens includes the strategic placement of round tables, fountains and flowerbeds.
• Calculating piping and hose diameters from flow requirements
• The process of determining the necessary materials for circular signs, lids and logo decals requires calculation.
• The process of photography requires accurate measurement of lens diameters and apertures.
• The analysis of athletic track curves together with velodrome shapes represents an essential element in track and field athletics.
• The process of understanding engineering drawings for gears, pulleys and bearings requires specific knowledge.