Year 9 Rearranging Equations Worksheets
What is rearranging equations in maths?
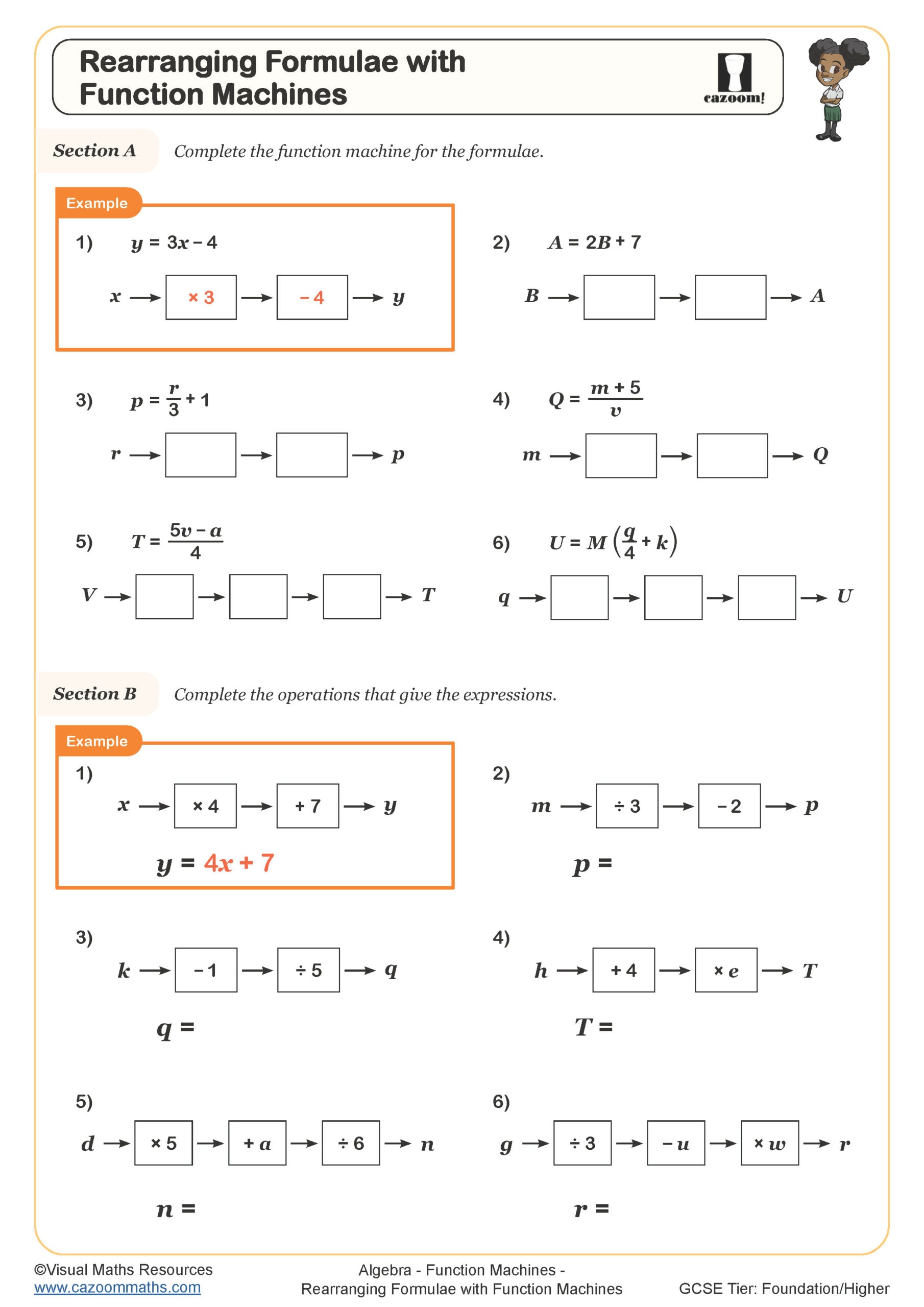
Rearranging equations, also called changing the subject of a formula, involves manipulating an equation so that a different variable stands alone on one side. This algebraic skill requires students to apply inverse operations in the reverse order they would use for solving, undoing each operation systematically until the desired variable is isolated. The National Curriculum expects Year 9 students to confidently rearrange linear equations and begin working with more complex formulae involving brackets and fractions.
A common error occurs when students subtract or divide without applying the operation to every term on both sides of the equation. For example, when rearranging 3x + 2 = y to make x the subject, students sometimes write x = y - 2 ÷ 3 instead of recognising that subtraction must happen before division. This misconception stems from confusing the order of operations when constructing expressions with the inverse sequence needed for rearrangement.
Which year groups learn rearranging equations?
These worksheets target Year 9 students at Key Stage 3, where rearranging equations forms a cornerstone of the algebra curriculum. This sits between basic equation solving in Years 7-8 and the more demanding algebraic manipulation required for GCSE, where students must rearrange complex formulae in science, change the subject when variables appear multiple times, and handle quadratic rearrangements at Higher tier.
The progression through Year 9 typically moves from making x the subject in simple linear equations like y = mx + c to tackling formulae where the required variable appears inside brackets or denominators. Students begin with cases requiring two or three steps, then advance to equations demanding careful planning about which operation to undo first, particularly when dealing with terms like a(b + x) or p/q = r where x is buried within the structure.
How do you rearrange equations with fractions?
Rearranging equations containing fractions requires students to eliminate the fraction first by multiplying both sides by the denominator. For instance, to make h the subject of v = u + ah/2, students multiply both sides by 2 to give 2v = 2u + ah, then subtract 2u before finally dividing by a. Many students lose marks in assessments by attempting to manipulate the fraction itself rather than clearing it completely, or by forgetting to multiply every term when the fraction appears alongside other terms.
This skill connects directly to physics formulae where fractional relationships are fundamental. Kinetic energy (KE = ½mv²) requires rearrangement to find velocity from known energy and mass, whilst electrical resistance calculations using R = V/I must be rearranged depending on which quantity needs calculating. Engineers and scientists regularly manipulate such formulae, making this more than an abstract exercise but a practical tool for problem-solving across STEM disciplines.
How can these worksheets help students master rearranging equations?
The worksheets provide structured progression through different equation types, allowing students to build confidence with simpler rearrangements before tackling multi-step problems. Each sheet typically groups similar problem types together so students can recognise patterns in the approach needed, then mixes question styles to develop flexibility in choosing appropriate strategies. The answer sheets show not just final answers but enable teachers to identify exactly where errors occur in students' working, whether in applying inverse operations, dealing with negative terms, or maintaining equation balance.
These resources work effectively for targeted intervention with students who struggle to connect equation solving with rearrangement, as homework to consolidate classwork, or as starter activities to maintain fluency. Paired work where one student rearranges whilst their partner checks each step against the answers helps develop mathematical communication and error-spotting skills. Teachers often use individual questions as worked examples on the board, then release students to attempt similar problems independently with immediate feedback available.