Fraction Quick Rules RESOURCE (FREE DOWNLOAD)

This resource shows brief rules and examples for adding, subtracting, multiplying and dividing fractions. Useful as a poster or handout.

Fraction Rules: A Complete Guide to Adding, Subtracting, Multiplying, and Dividing Fractions

Fractions are an essential part of the KS2 and KS3 maths curriculum. Understanding the basic rules of fractions makes many types of calculations easier. Our number teaching resource, ‘Fraction Quick Rules’, will help you teach and understand fraction rules step by step. This guide covers addition, subtraction, multiplication, and division of fractions.

Basic Rules of Fractions

• A fraction has a numerator (top) and a denominator (bottom).
• To simplify a fraction, divide the numerator and denominator by their greatest common factor (GCF).
• Always express answers in their simplest form or as a mixed number if required.

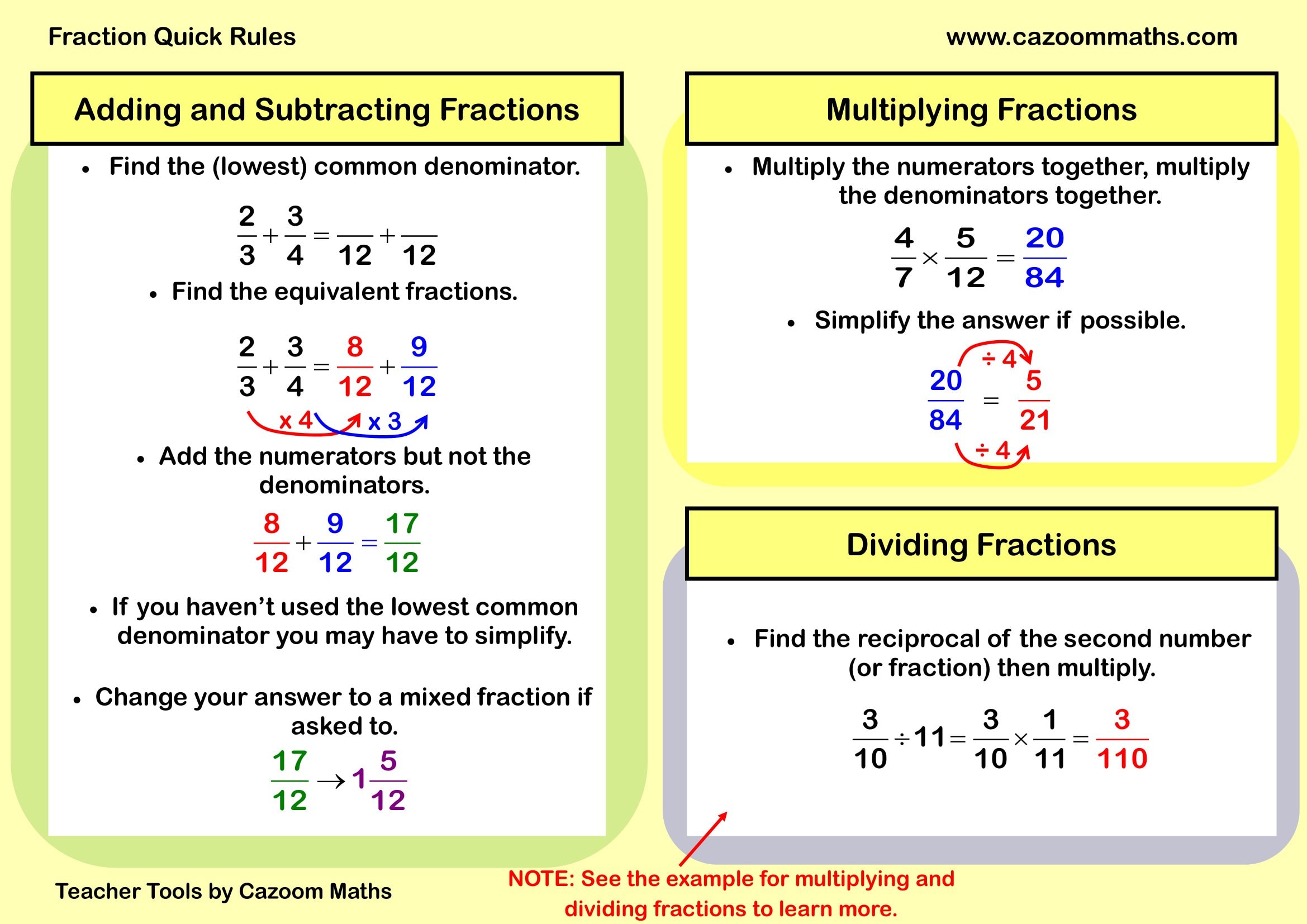
Adding and Subtracting Fractions

When adding or subtracting fractions, the denominators must be the same.

Step 1: Find a Common Denominator

Convert fractions to have the same denominator by finding the lowest common denominator (LCD).

Example:
\[
\frac{2}{3} + \frac{3}{4}
\]

The LCD of 3 and 4 is 12. Convert both fractions:

\[
\frac{2}{3} = \frac{8}{12}, \quad \frac{3}{4} = \frac{9}{12}
\]

Step 2: Add the Numerators

\[
\frac{8}{12} + \frac{9}{12} = \frac{17}{12}
\]

Step 3: Convert to a Mixed Number (if needed)

\[
\frac{17}{12} = 1 \frac{5}{12}
\]

Final Answer: \(1 \frac{5}{12}\)

Note: For subtraction, follow the same steps but subtract the numerators.

---

Multiplying Fractions

Step 1: Multiply the Numerators

Step 2: Multiply the Denominators

Step 3: Simplify the Answer

Example:
\[
\frac{4}{7} \times \frac{5}{12}
\]

\[
\frac{4 \times 5}{7 \times 12} = \frac{20}{84}
\]

Now simplify by dividing by 4:
\[
\frac{20}{84} = \frac{5}{21}
\]

Final Answer: \( \frac{5}{21} \)

---

Dividing Fractions

To divide fractions, flip the second fraction (reciprocal) and multiply.

Example:
\[
\frac{3}{10} \div \frac{11}{1}
\]

Step 1:

Flip the second fraction:
\[
\frac{1}{11}
\]

Step 2:

Multiply:
\[
\frac{3}{10} \times \frac{1}{11} = \frac{3}{110}
\]

Final Answer: \( \frac{3}{110} \)

---

Quick Tips for Working with Fractions

• Always simplify your answers where possible.
• Convert improper fractions to mixed numbers when required.
• Use cross-multiplication to compare fractions.