Laws of Indices RESOURCE (FREE DOWNLOAD)
Laws of Indices RESOURCE DESCRIPTION
This example resource gives examples of all index laws in algebraic and numerical form. Index laws cover those required at foundation and higher tier GCSE. Ideal as a display poster or printable revision tool for students.

RELATED TO Laws of Indices
What is the Resource?
This free PDF offers a detailed and accessible reference sheet on the laws of indices, also known as index notation or powers. It includes all essential rules, such as multiplying indices, dividing indices, zero indices, negative indices, and fractional indices. Designed for secondary school learners, this resource simplifies a complex topic into manageable steps.
Why Are the Laws of Indices Important?
Understanding the laws of indices is fundamental for advanced maths and has practical applications in real-world scenarios:
- Scientific Notation: Index notation is vital for representing very large or very small numbers in fields like physics, astronomy, and engineering.
- Financial Growth: Compound interest and exponential growth rely on indices to calculate changes over time in investments and savings.
- Programming and Coding: Indices form the basis of binary systems, which are the foundation of computing and programming languages.
- Exponential Models: Used in predicting the spread of diseases, population growth, and technological advancements.
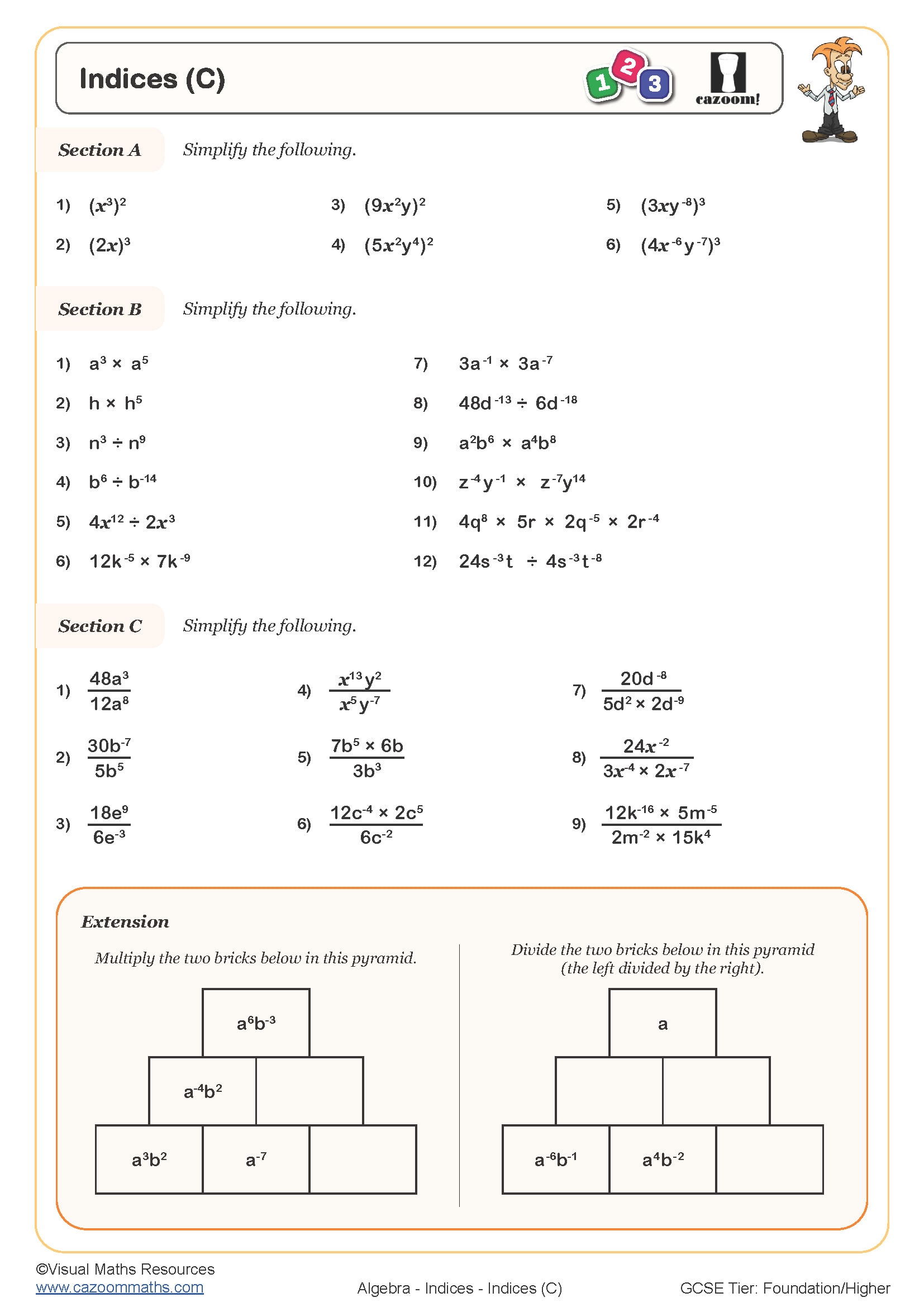
Key Laws of Indices Covered
1. Multiplication Rule
When multiplying terms with the same base, add their powers.
Formula: am × an = am+n
Example: 23 × 24 = 23+4 = 27
2. Division Rule
When dividing terms with the same base, subtract their powers.
Formula: am ÷ an = am-n
Example: 57 ÷ 53 = 57-3 = 54
3. Power of a Power Rule
When raising a power to another power, multiply the exponents.
Formula: (am)n = am×n
Example: (102)3 = 102×3 = 106
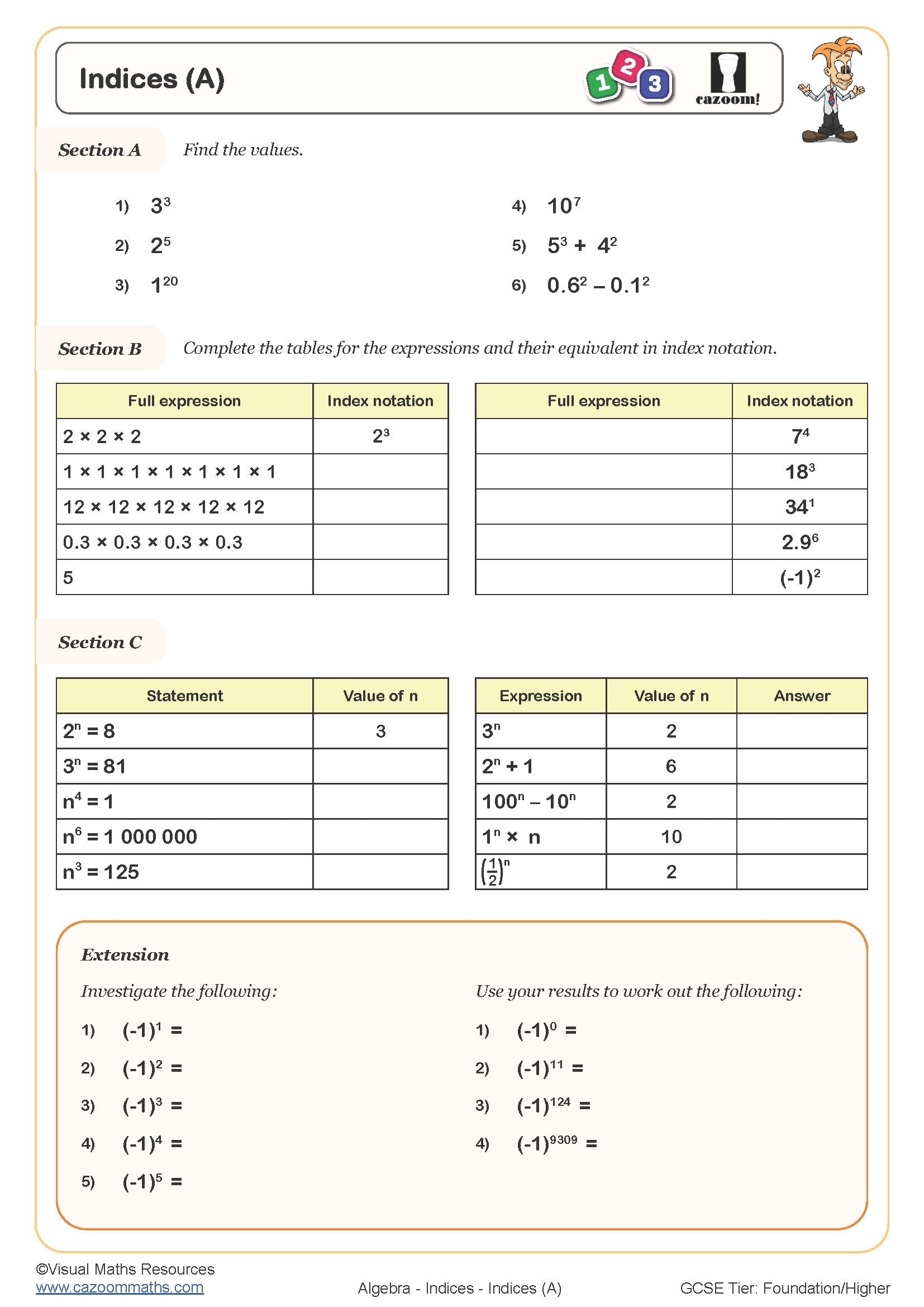
4. Zero Index Rule
Any number raised to the power of zero is equal to one, provided the base is not zero.
Formula: a0 = 1
Example: 340 = 1
5. Negative Indices Rule
A term with a negative index represents the reciprocal of the term with a positive index.
Formula: a-m = 1/am
Example: 9-2 = 1/92 = 1/81
6. Fractional Indices Rule
A fractional index represents a root. The denominator indicates the type of root, and the numerator indicates the power.
Formula: am/n = n√am
Example: 491/2 = √49 = 7
How Can This Resource Help?
This comprehensive guide builds confidence and fluency in applying indices rules:
- Clear Summaries: Each rule is explained with simple formulas to aid understanding.
- Common Errors Highlighted: Helps students avoid mistakes when simplifying expressions with indices.
- Builds Fluency: Reduces anxiety by providing repeated practice, making indices rules second nature.
- Printable Reference: Ideal for use in lessons, as a classroom display, or as part of revision packs.
Benefits for Learners
- Simplifies understanding of indices rules with clear explanations.
- Prepares students for more advanced topics in algebra, exponential functions, and scientific notation.
- Encourages problem-solving by helping students simplify complex expressions.
- Provides a strong foundation for applications in STEM fields and real-world scenarios.
Who Is This For?
- Teachers: A handy teaching aid to explain and reinforce the laws of indices in the classroom.
- Students: A valuable tool for revising and mastering index notation.
- Parents: A resource for supporting children with maths homework and additional practice.
Discover More!
Explore our range of worksheets designed to help students practise fractional indices and other rules of indices. These resources are available in easy-to-download PDF formats, perfect for revision or homework tasks.