KS3 Compound Measures Worksheets
All worksheets are created by the team of experienced teachers at Cazoom Maths.
What are compound measures in maths?
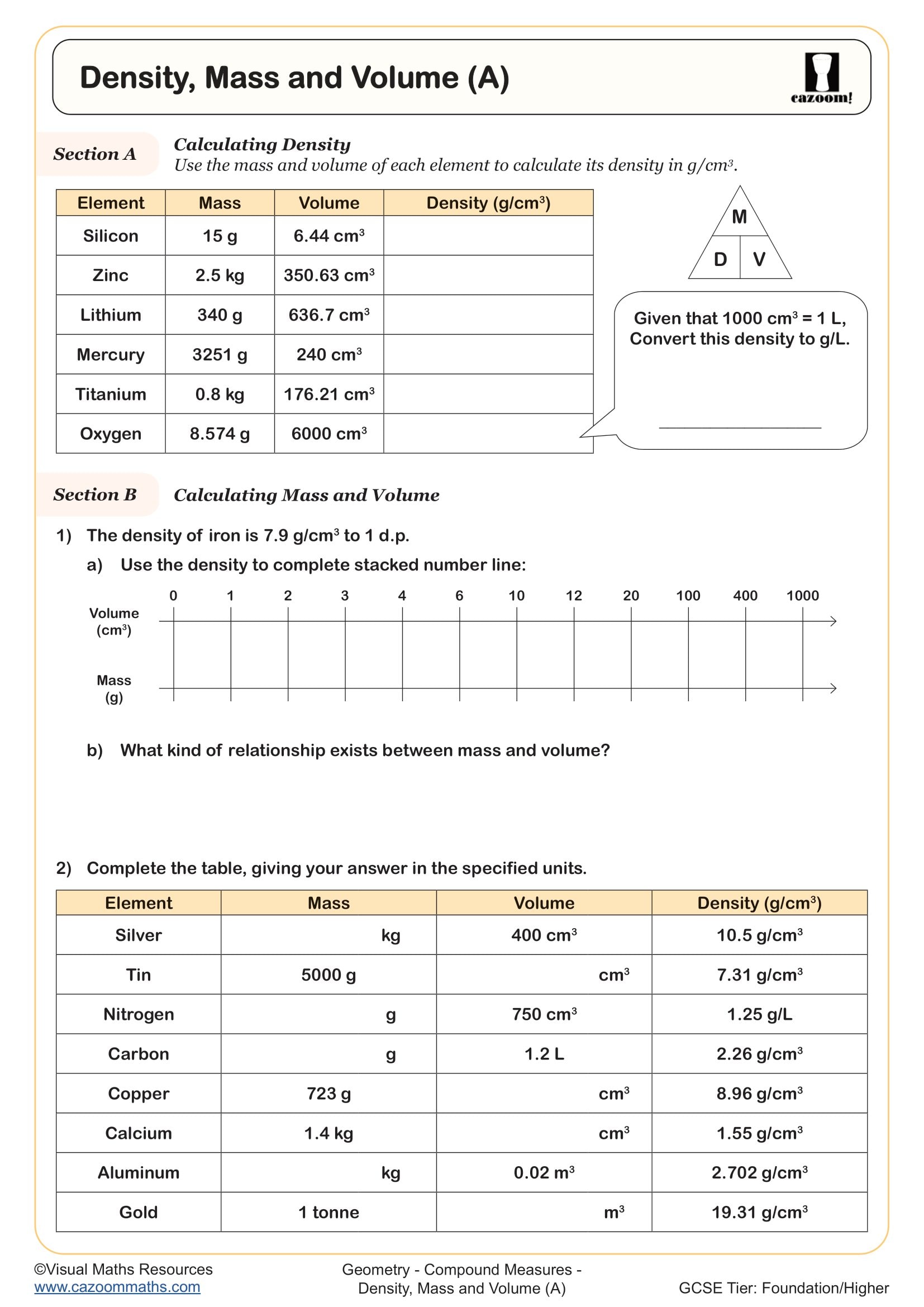
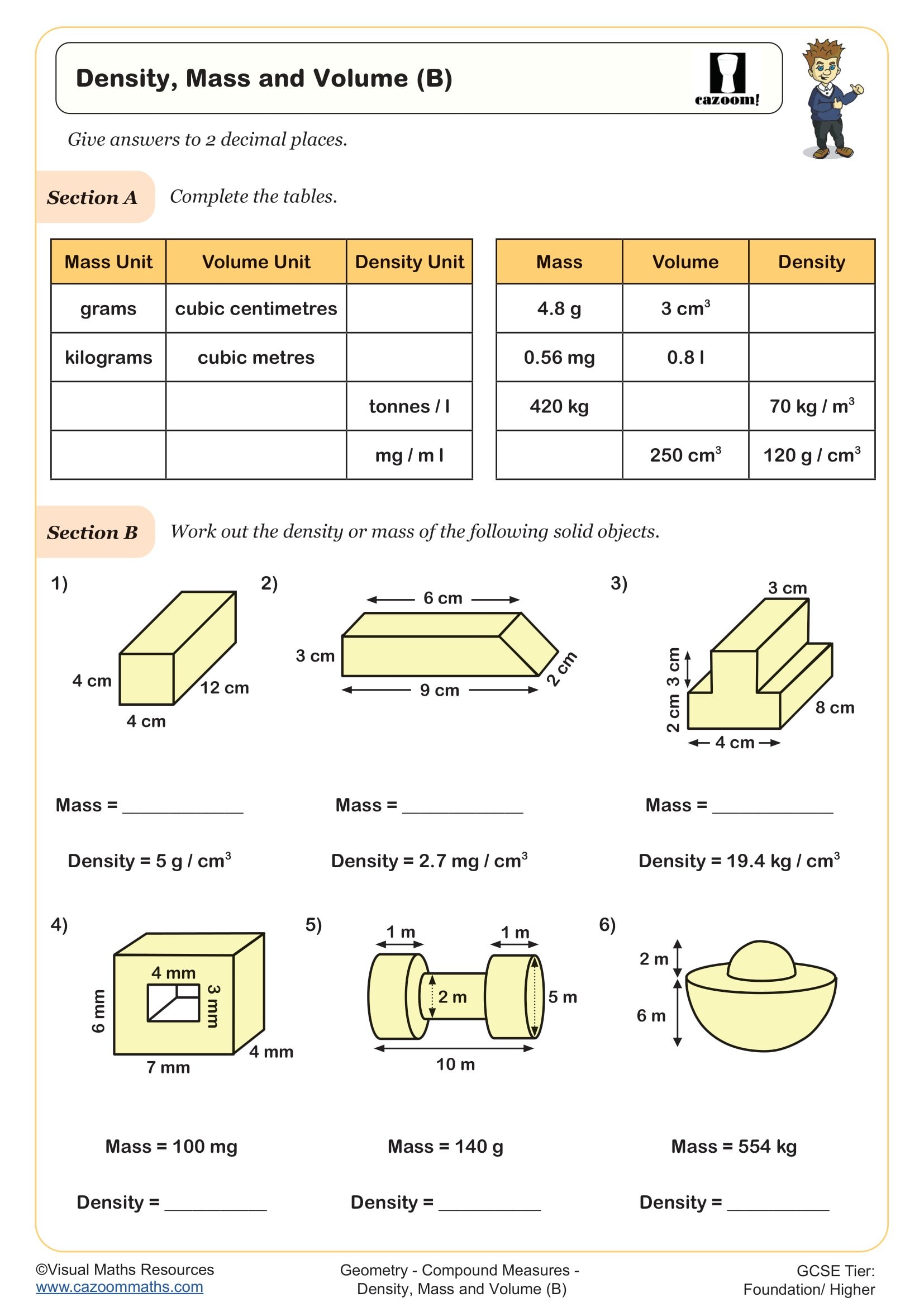
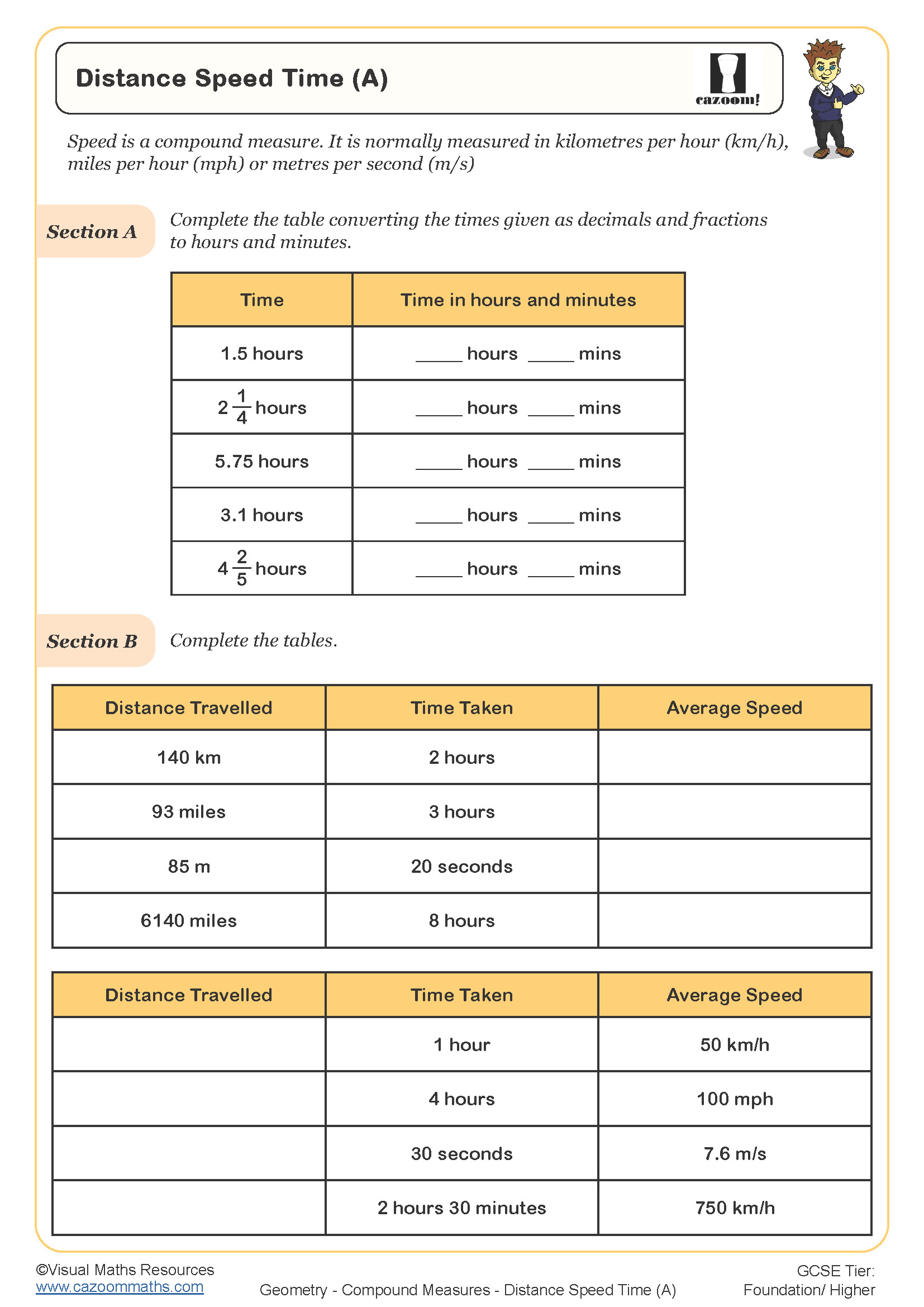
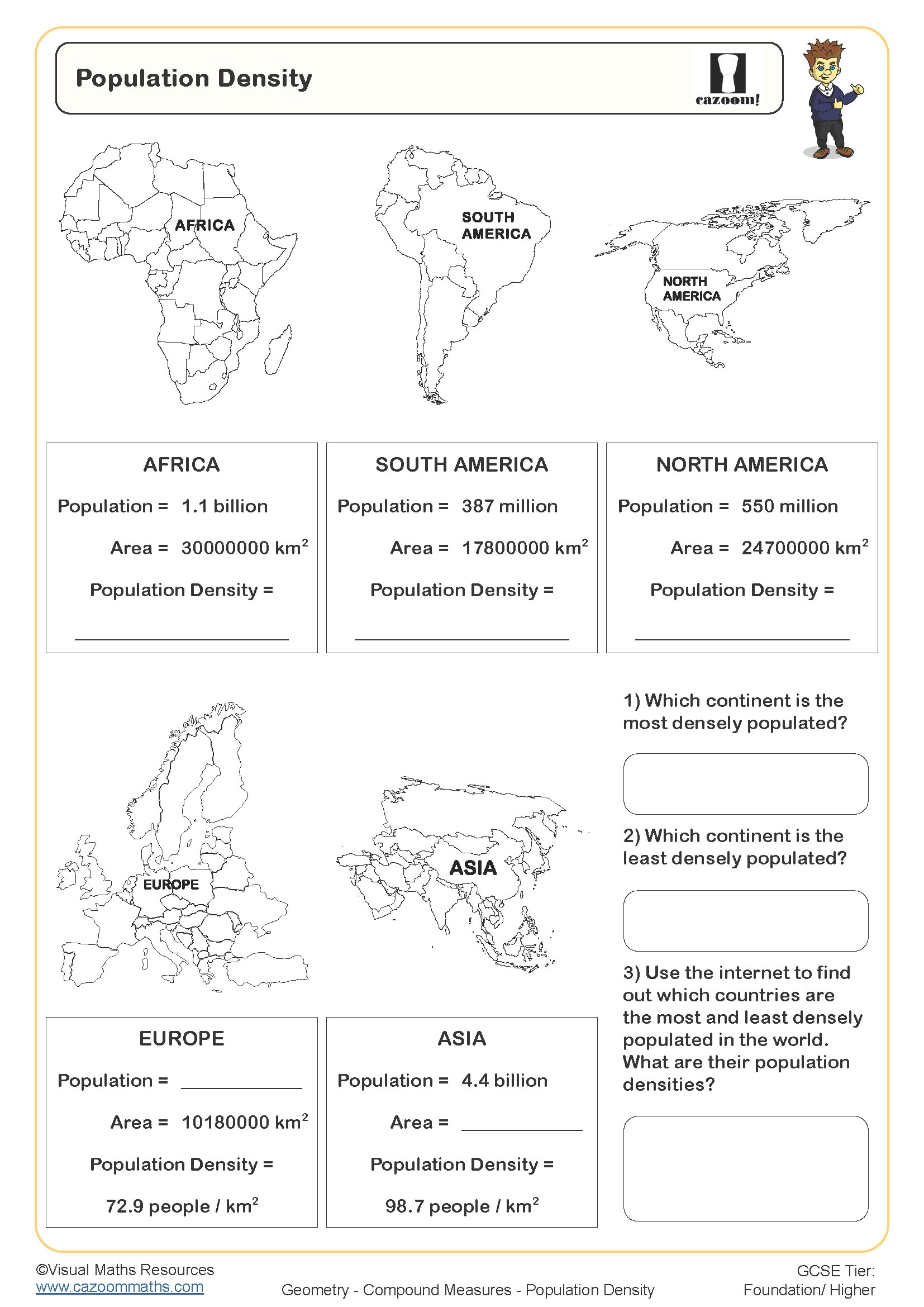
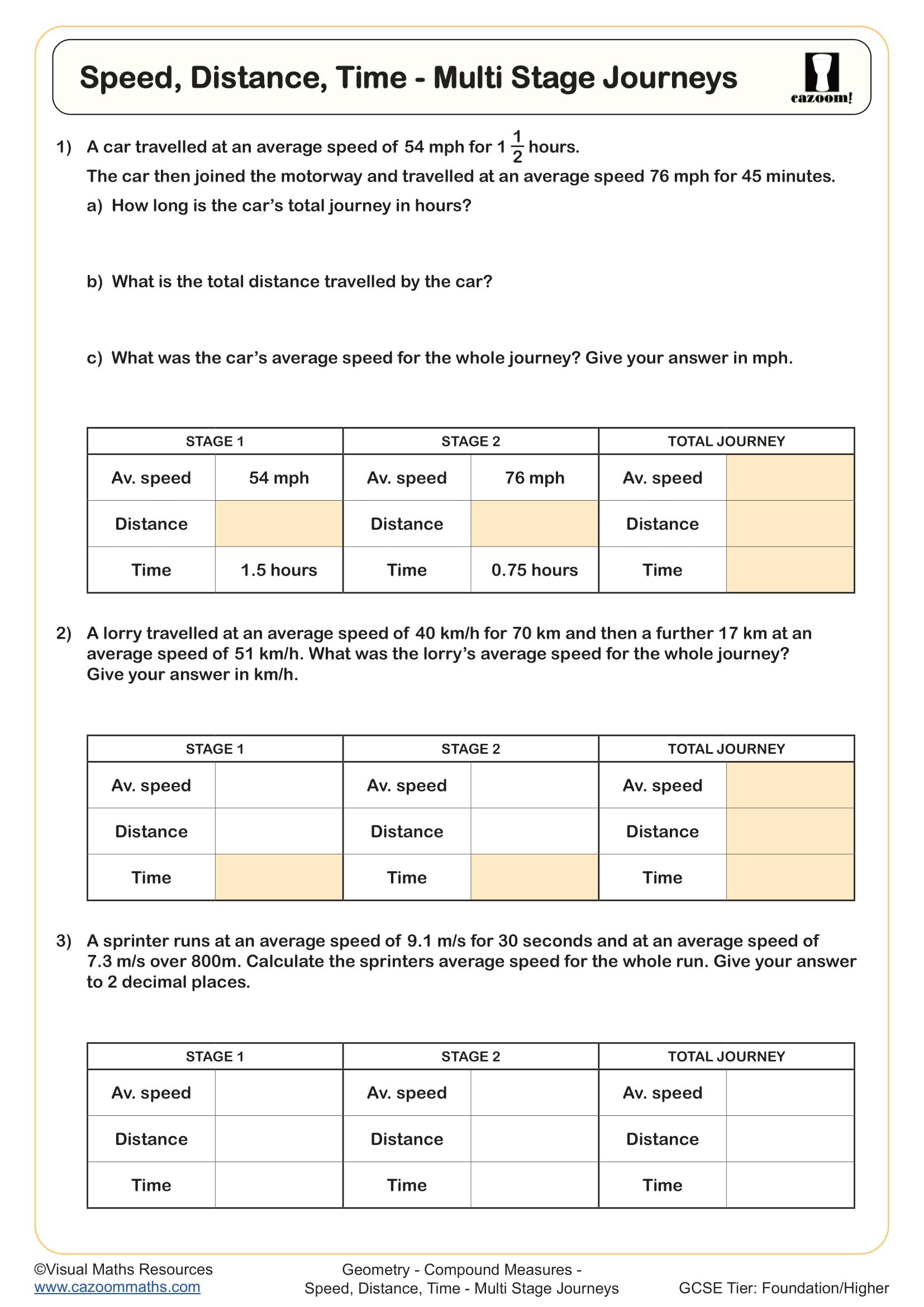
Compound measures are quantities formed by combining two or more base units, such as speed (distance per time), density (mass per volume) and pressure (force per area). In the KS3 National Curriculum, students learn to calculate and interpret these measures, moving beyond simple measurements like length or mass to understand rates and ratios expressed as combined units.
Many teachers observe that students treat compound measures as separate formulae to memorise rather than understanding the underlying relationship. For example, with density = mass ÷ volume, students often forget that mass = density × volume or volume = mass ÷ density are simply rearrangements. This reliance on memorisation rather than understanding causes difficulties when exam questions present unfamiliar contexts or require formula rearrangement.
Which year groups cover compound measures?
These worksheets target Year 8 and Year 9 students, covering the KS3 compound measures curriculum expectations. Students typically encounter speed, distance and time calculations first in Year 8, establishing the foundation for understanding rates and compound units. Density and pressure are then introduced as students develop confidence with the underlying principles.
Progression across these year groups involves increasing complexity in both calculations and contexts. Year 8 students work with straightforward problems using standard units, whilst Year 9 students tackle multi-step problems requiring unit conversions, formula rearrangement and application to unfamiliar contexts. By the end of Year 9, students should confidently manipulate compound measure formulae and select appropriate units for their answers.
Why is understanding density important beyond maths lessons?
Density calculations underpin numerous scientific and engineering applications, from explaining why objects float or sink to designing materials for specific purposes. Students learn that density measures how much mass is packed into a given volume, expressed in units like g/cm³ or kg/m³. This concept connects directly to material science, where engineers select materials based on their density properties for applications ranging from aircraft construction to medical implants.
In real-world STEM contexts, density calculations help scientists identify unknown substances, quality control teams detect manufacturing defects, and marine engineers determine ship stability. Understanding that changing either mass or volume affects density allows students to predict material behaviour. For instance, why expanded polystyrene provides effective insulation (low density means trapped air pockets) or why lead makes effective radiation shielding (high density means tightly packed atoms).
How do these worksheets build confidence with compound measures?
The worksheets provide graduated practice starting with direct substitution into formulae before progressing to problems requiring rearrangement and unit conversion. Students work through calculations systematically, developing familiarity with the relationships between compound measure components. The structured approach helps students recognise which formula to apply and how to manipulate it based on the information given and what needs finding.
Teachers use these resources flexibly across different classroom contexts. They work well for initial practice after introducing a new compound measure, allowing students to consolidate their understanding through repetition with varied values. The worksheets also serve effectively as homework tasks, intervention materials for students who need additional support, or revision resources before assessments. Having answer sheets available means students can self-check their working, identifying whether errors occur in formula rearrangement, calculation or unit conversion stages.