KS3 Decimals Worksheets
Adding and Subtracting Decimals

Column Addition - Decimals (B)

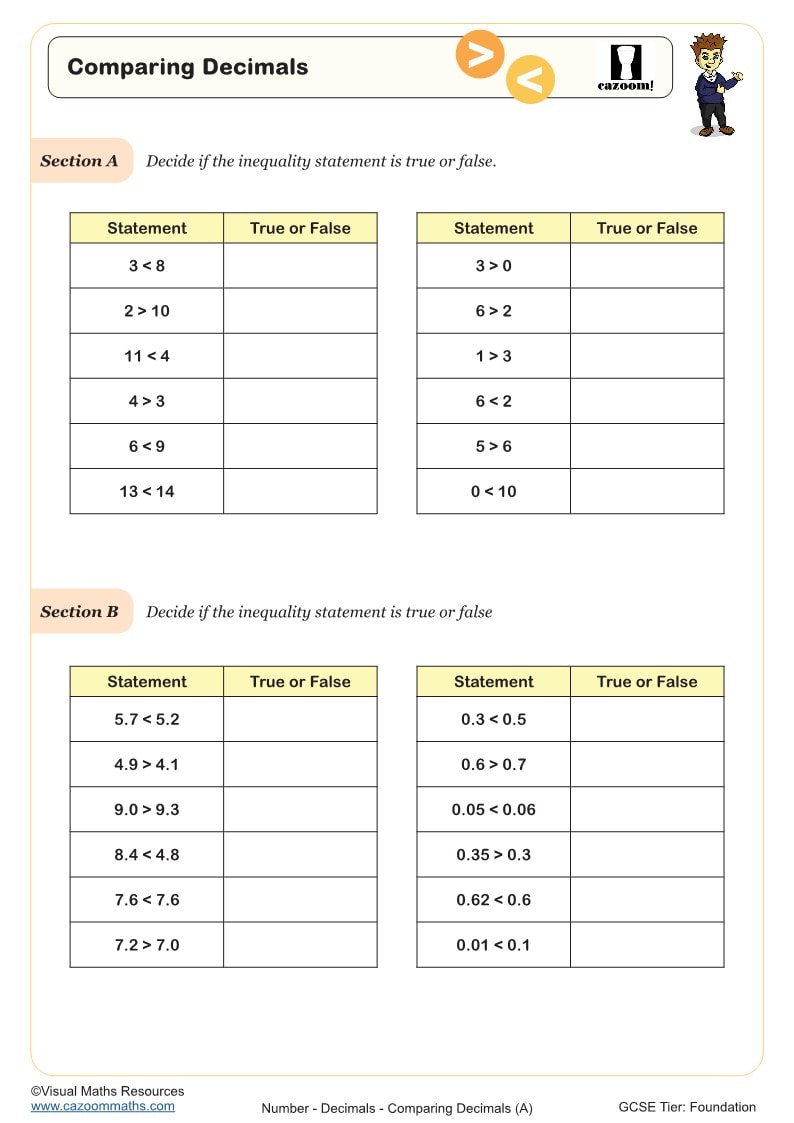
Comparing Decimals
Converting Between Minutes and Hours (B)

Decimal Operations Mixed Exercise

Decimal Operations Ten Minute Challenge

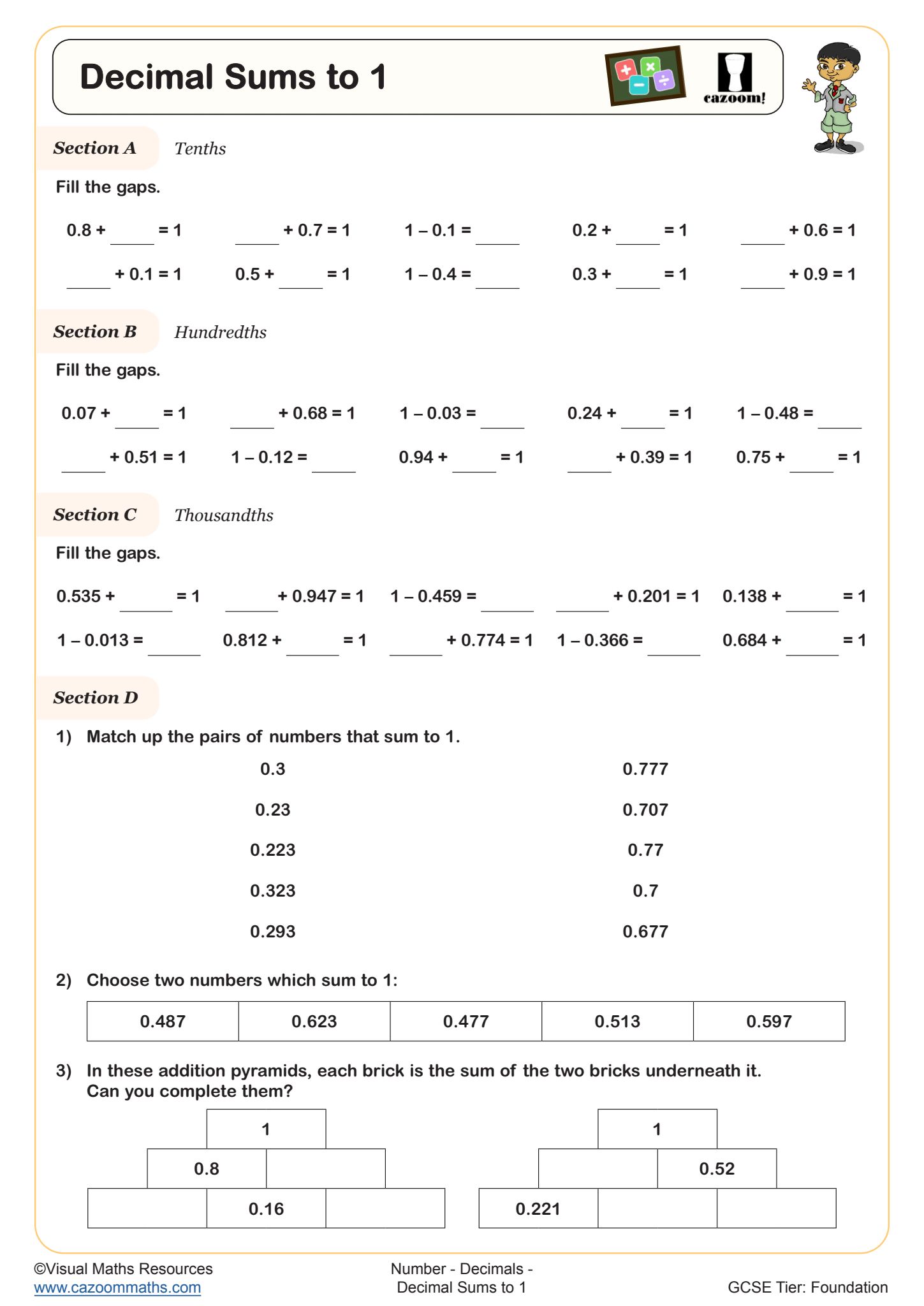
Decimal Sums to 1
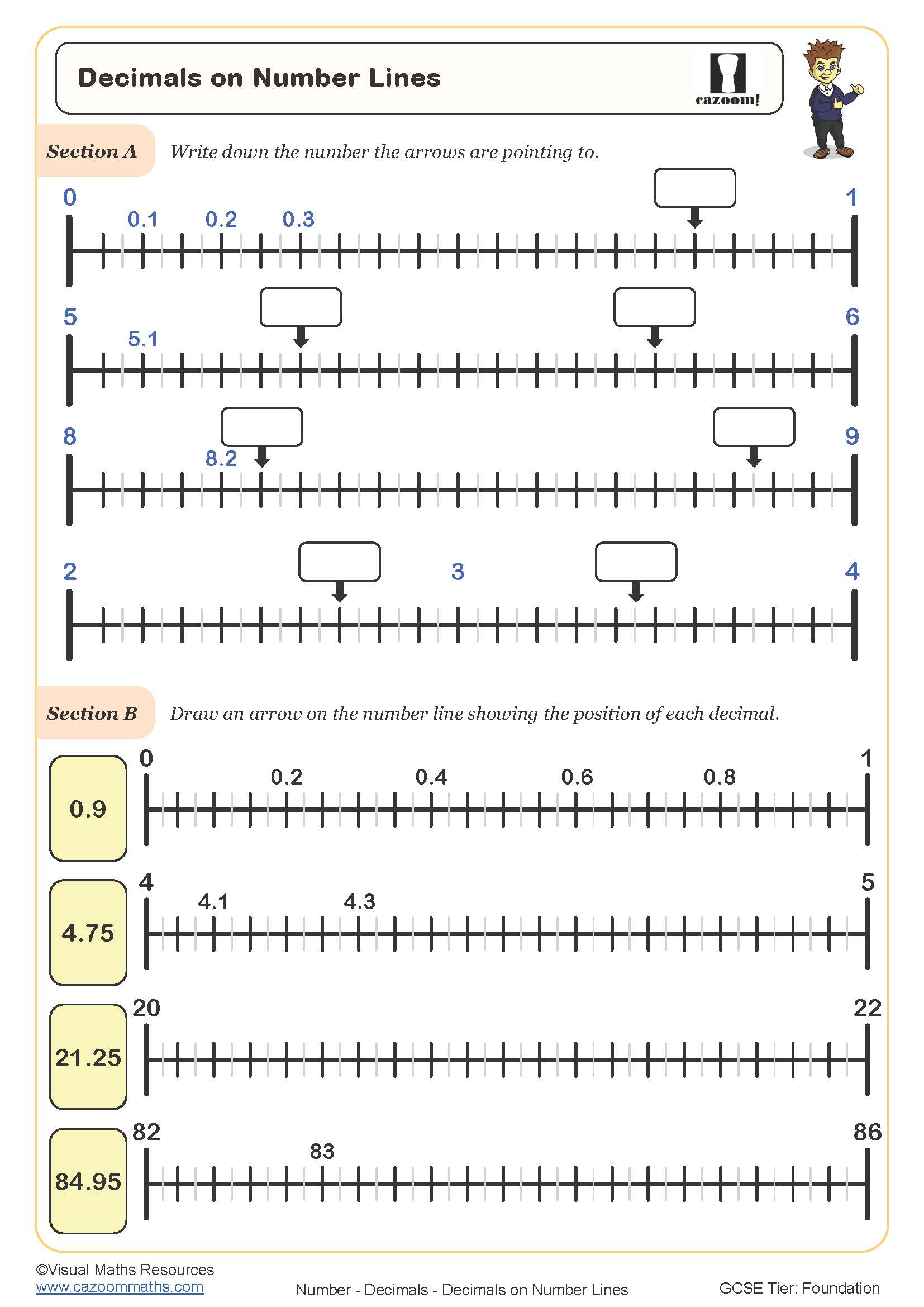
Decimals on Number Lines
Dividing by Decimals

Dividing Decimals (A)

Dividing Decimals (B)

Multiply Decimals by Integers

Multiplying and Dividing Decimals

Multiplying Decimals - Using Known Facts

Multiplying Decimals (A)

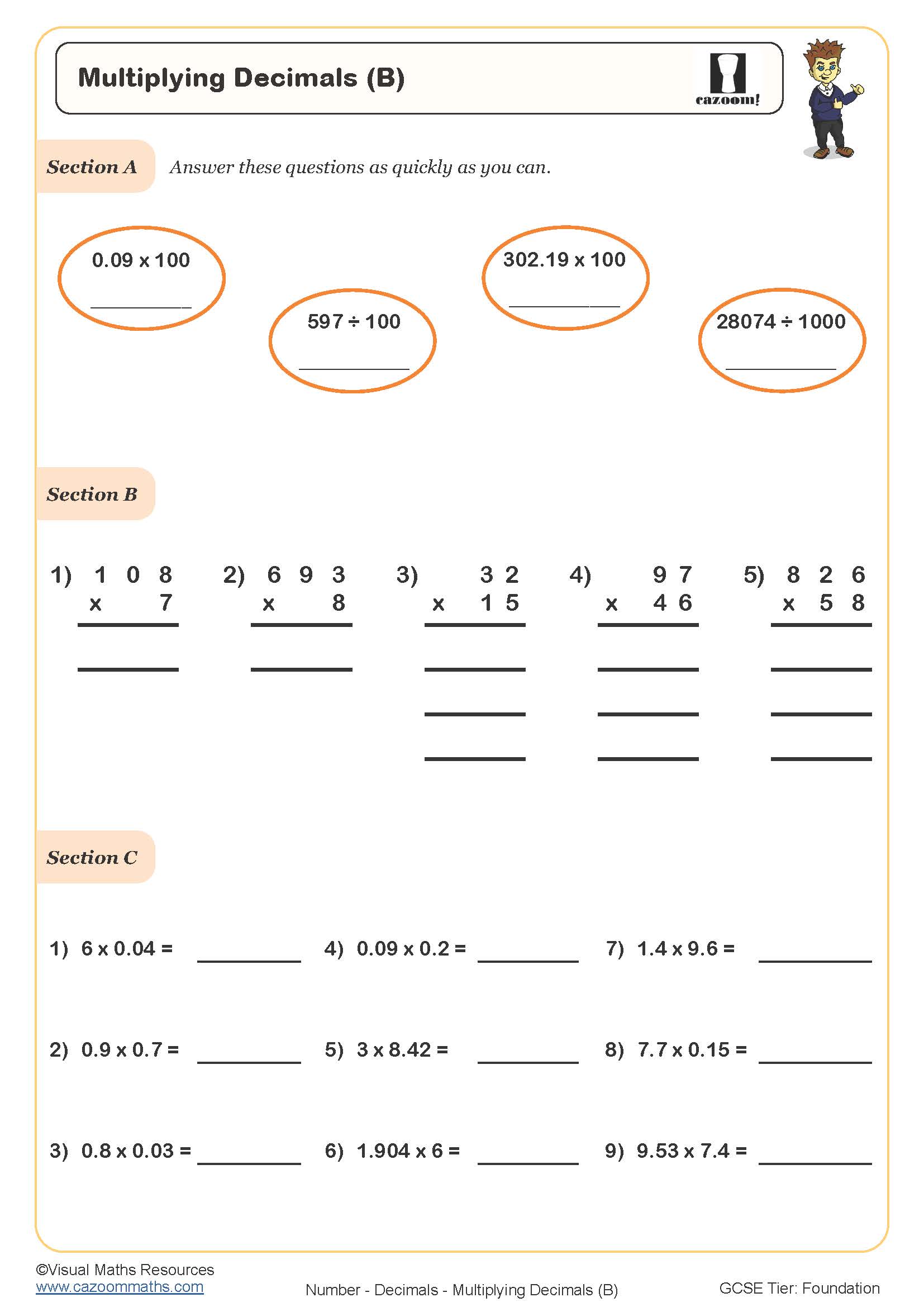
Multiplying Decimals (B)
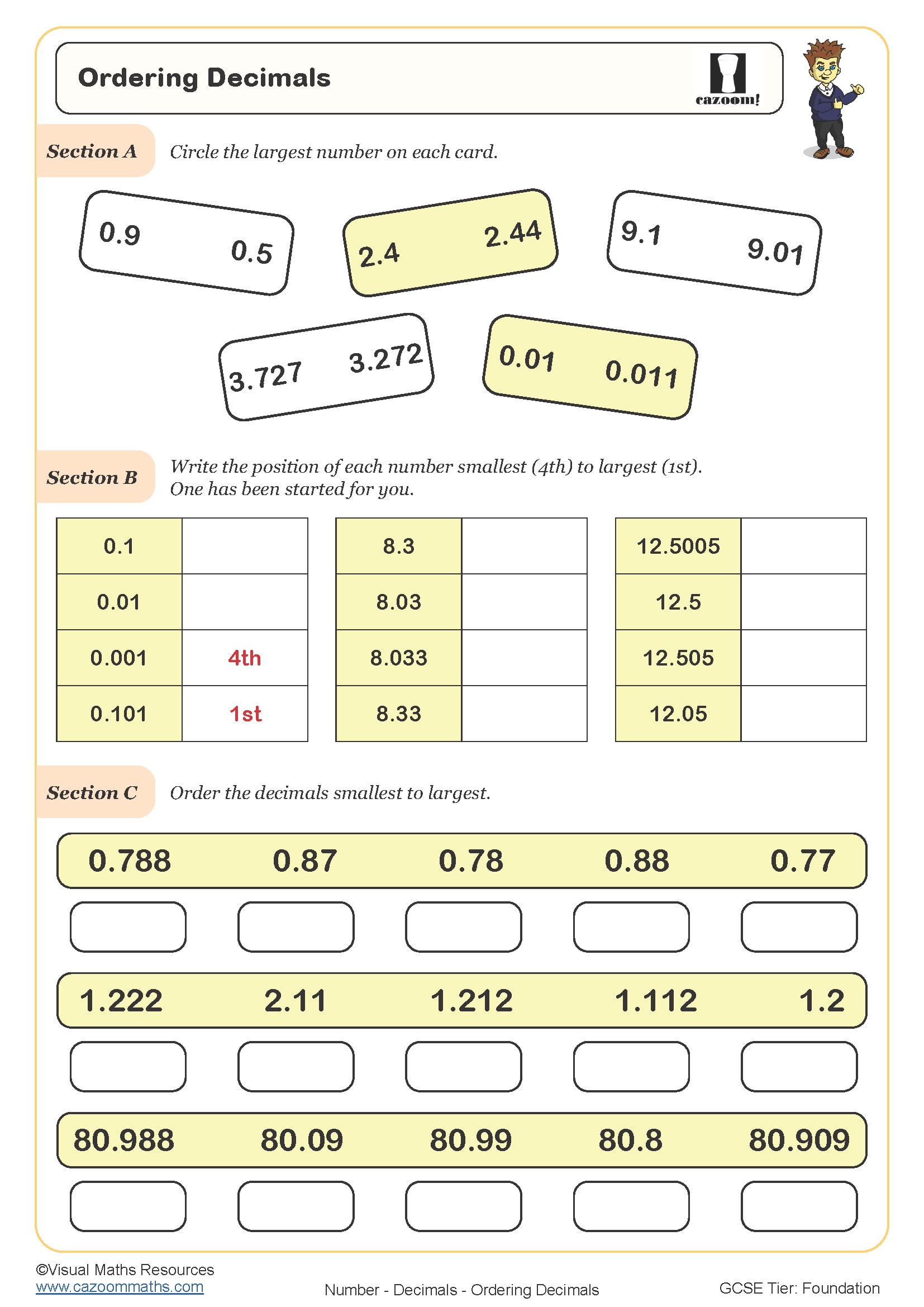
Ordering Decimals
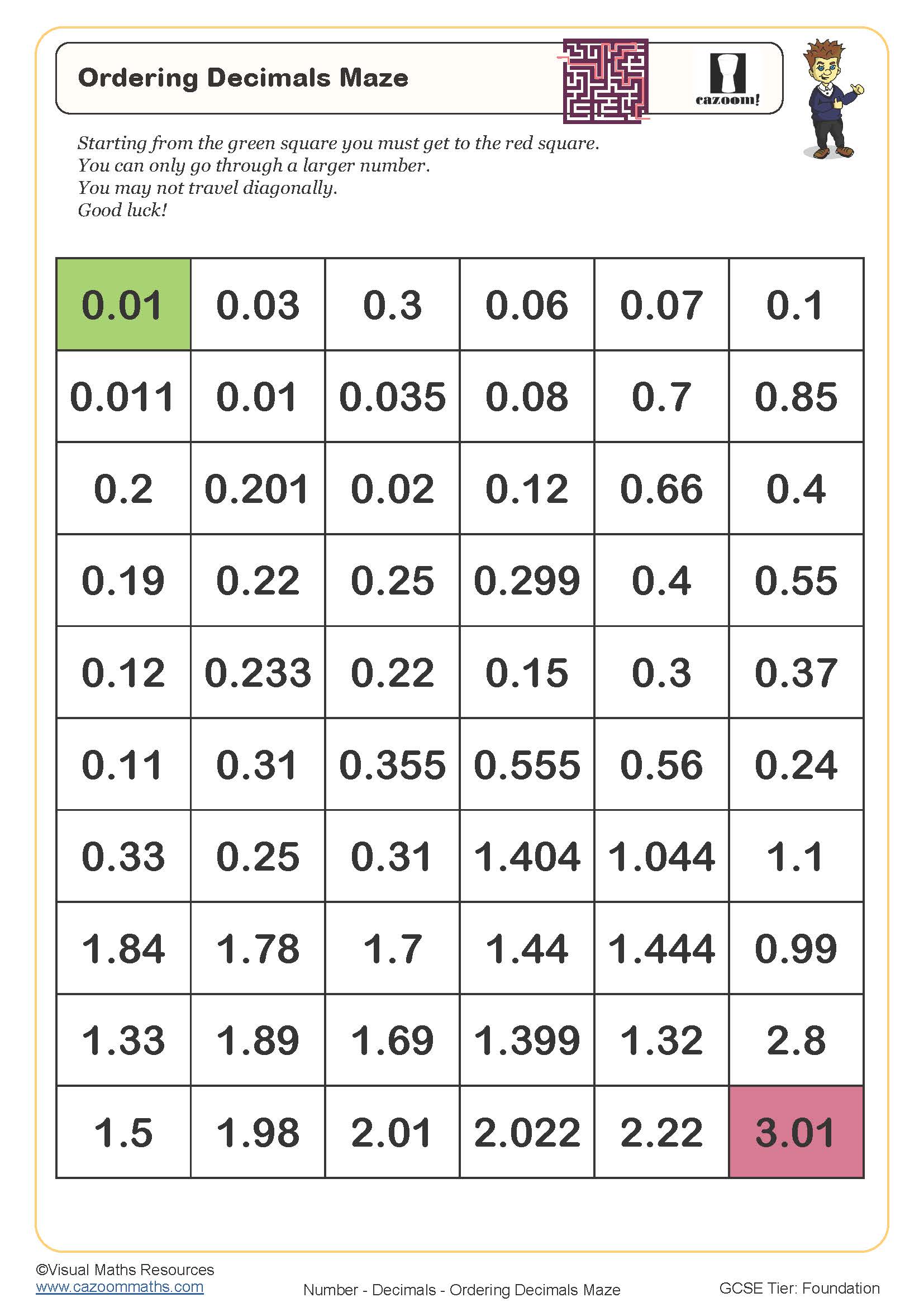
Ordering Decimals Maze
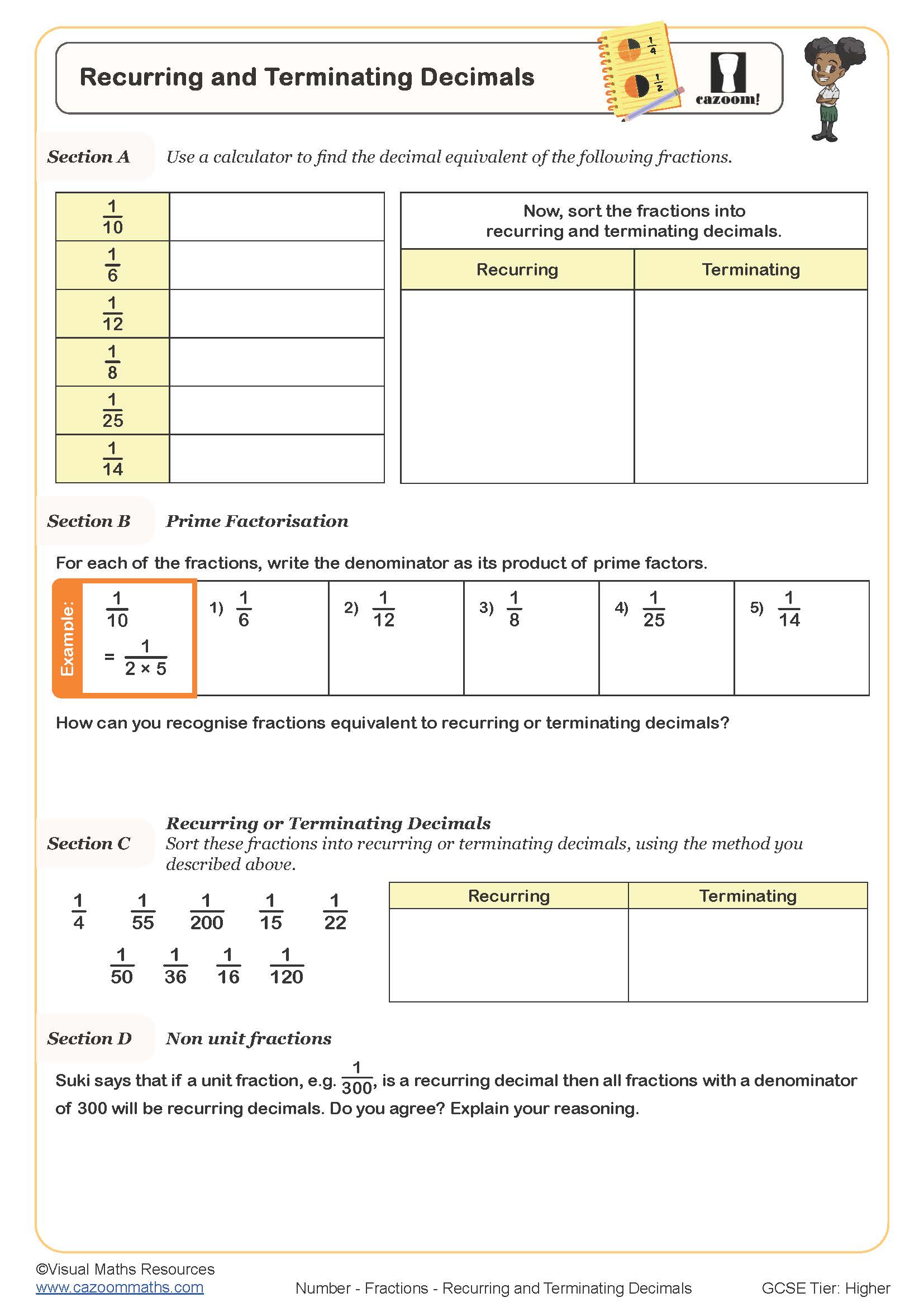
Recurring and Terminating Decimals
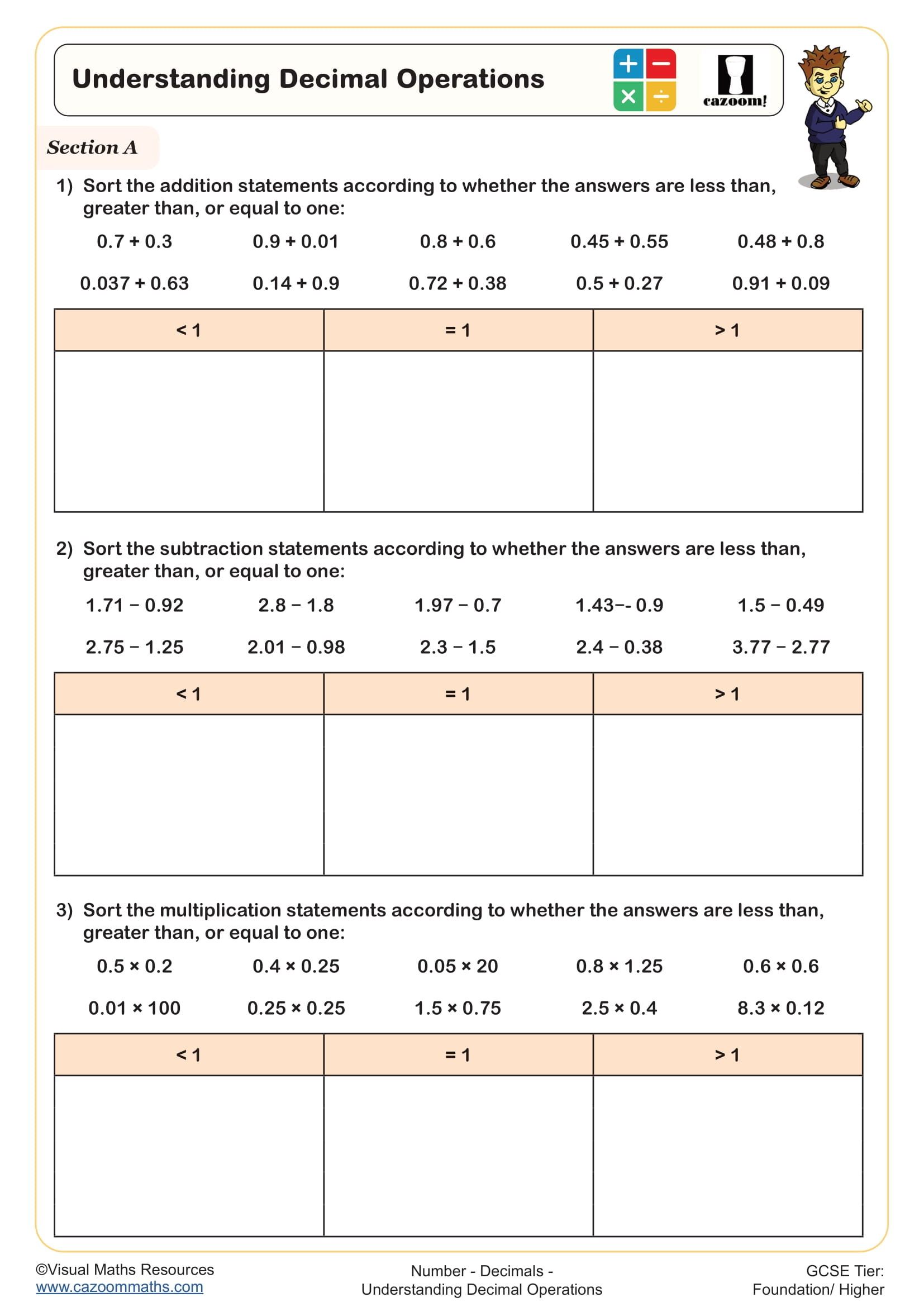
Understanding Decimal Operations
What decimal skills do KS3 students need to master?
KS3 students build on primary foundation work to develop confidence with more complex decimal operations and conversions. The National Curriculum expects students to multiply and divide decimals by whole numbers and powers of 10, order and compare decimals confidently, and convert fluently between fractions, decimals, and percentages. Students also need to understand terminating versus recurring decimals and apply decimal calculations in contexts like money, measurement, and data handling.
A common weakness appears when students multiply decimals by decimals, such as 0.3 × 0.4. Many incorrectly place the decimal point, arriving at 1.2 instead of 0.12, because they fail to count total decimal places in both factors. Exam mark schemes consistently penalise this error, particularly in GCSE papers where decimal multiplication appears in area, probability, and ratio questions without explicit instruction to "show your working".
Which year groups cover decimals at KS3?
These worksheets support Year 7, Year 8, and Year 9 students working through the KS3 programme of study. Year 7 typically focuses on consolidating understanding of decimal place value, ordering decimals, and performing addition and subtraction with up to three decimal places. Students also begin converting simple fractions to decimals and working with tenths and hundredths in practical contexts.
Year 8 and Year 9 extend this to multiplying and dividing decimals by decimals, understanding why certain fractions produce terminating decimals whilst others recur, and applying decimal calculations in increasingly complex problem-solving contexts. By Year 9, students should handle multi-step problems involving decimals confidently, preparing them for GCSE topics like standard form, bounds, and decimal estimation strategies that appear regularly in both Foundation and Higher tier papers.
Why do some fractions convert to terminating decimals?
A fraction converts to a terminating decimal when its denominator, in simplest form, contains only the prime factors 2 and 5. For example, 3/8 gives 0.375 because 8 = 2³, whilst 1/6 recurs as 0.1666... because 6 = 2 × 3, introducing a prime factor other than 2 or 5. Students often memorise this rule without understanding why it works, which limits their ability to predict decimal forms or explain their reasoning in written exam responses.
This concept connects directly to measurement and engineering contexts. Manufacturing tolerances frequently express acceptable variations in decimal millimetres, and machinists must know which fractional measurements (like 5/16 inch = 0.3125 inches) terminate for precise digital readout settings. In currency exchange and financial calculations, understanding terminating decimals prevents rounding errors that accumulate across multiple transactions, a skill students encounter in GCSE problem-solving questions involving percentage changes and compound interest.
How can teachers use these decimal worksheets effectively?
The worksheets provide structured practice that builds procedural fluency before introducing problem-solving applications. Each sheet targets specific skills, allowing teachers to assign focused practice on identified weak areas rather than generic "decimals" revision. Answer sheets enable students to self-mark during intervention sessions or homework, promoting immediate feedback and metacognitive reflection on errors. Teachers report this approach particularly effective for addressing persistent misconceptions around decimal place value.
Many teachers use these resources for differentiated starter activities, selecting appropriate difficulty levels for different groups within mixed-attainment classes. The worksheets work well for paired practice where students complete alternate questions then check each other's work against answer sheets, encouraging mathematical discussion about methods and errors. For homework, teachers often assign one worksheet per week across a half-term, gradually increasing complexity to consolidate understanding before moving to non-calculator problem-solving tasks that require confident decimal manipulation.