KS3 Pythagoras Worksheets
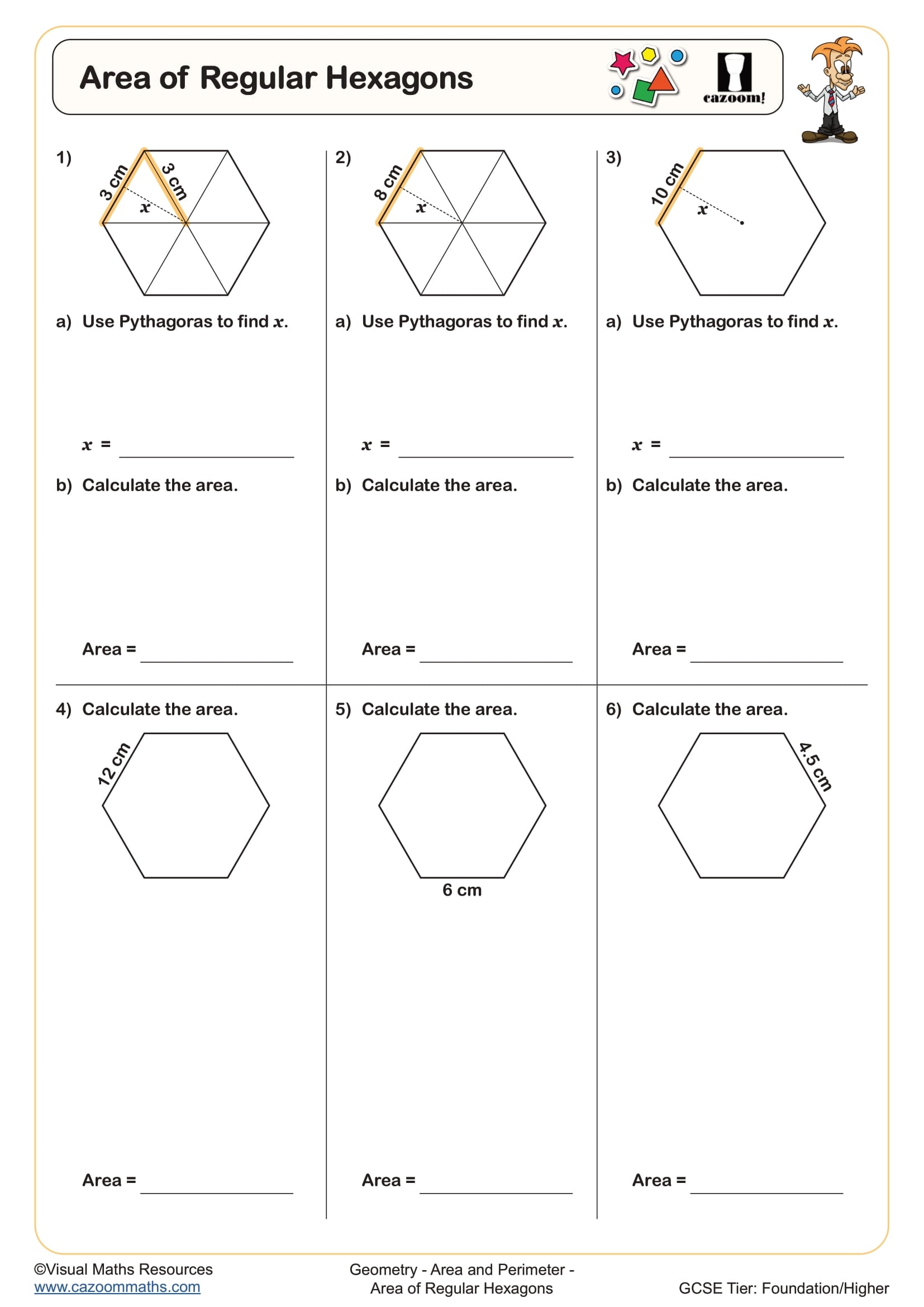
Area of Regular Hexagons
Identifying Right Angled Triangles

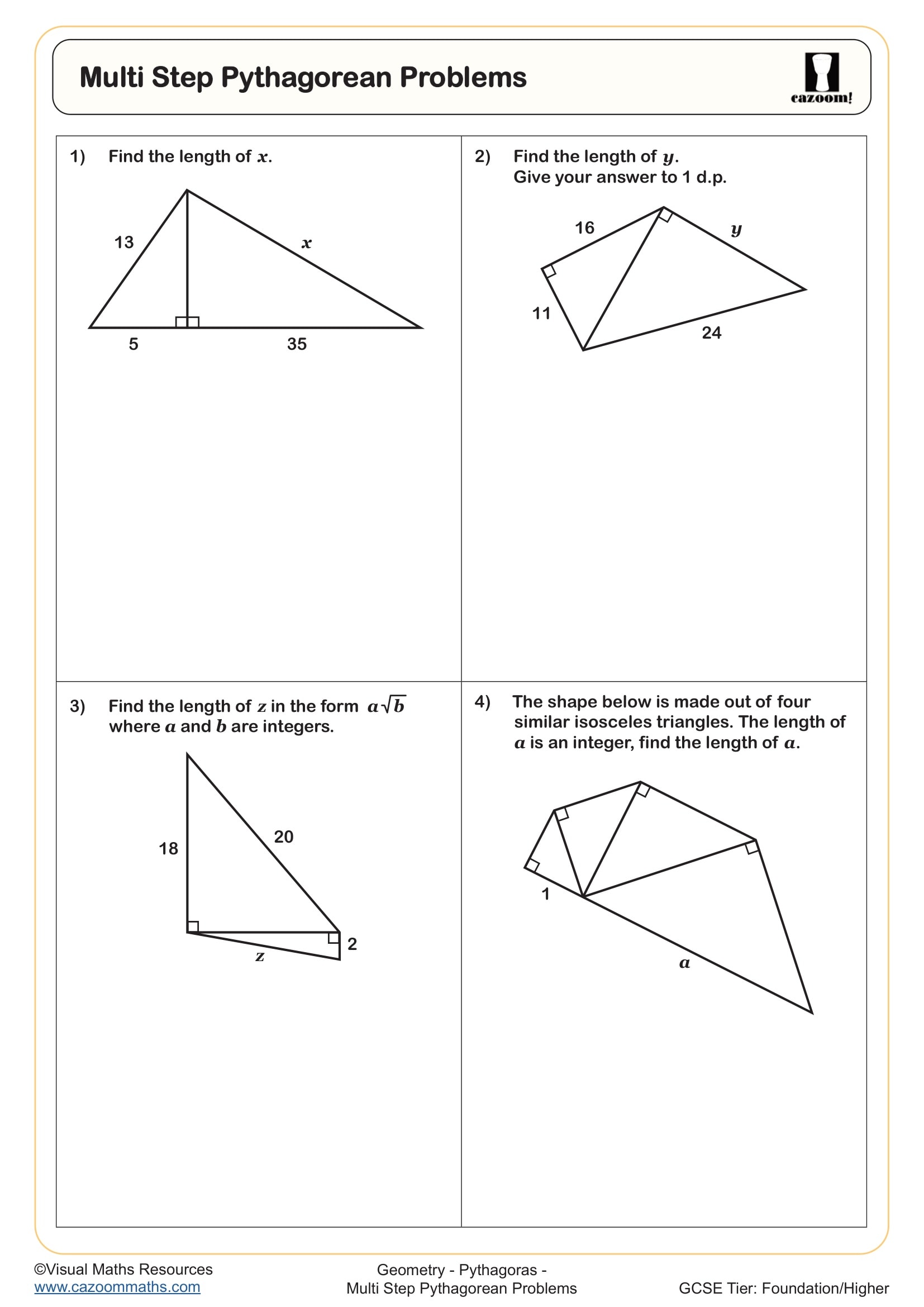
Multi Step Pythagorean Problems
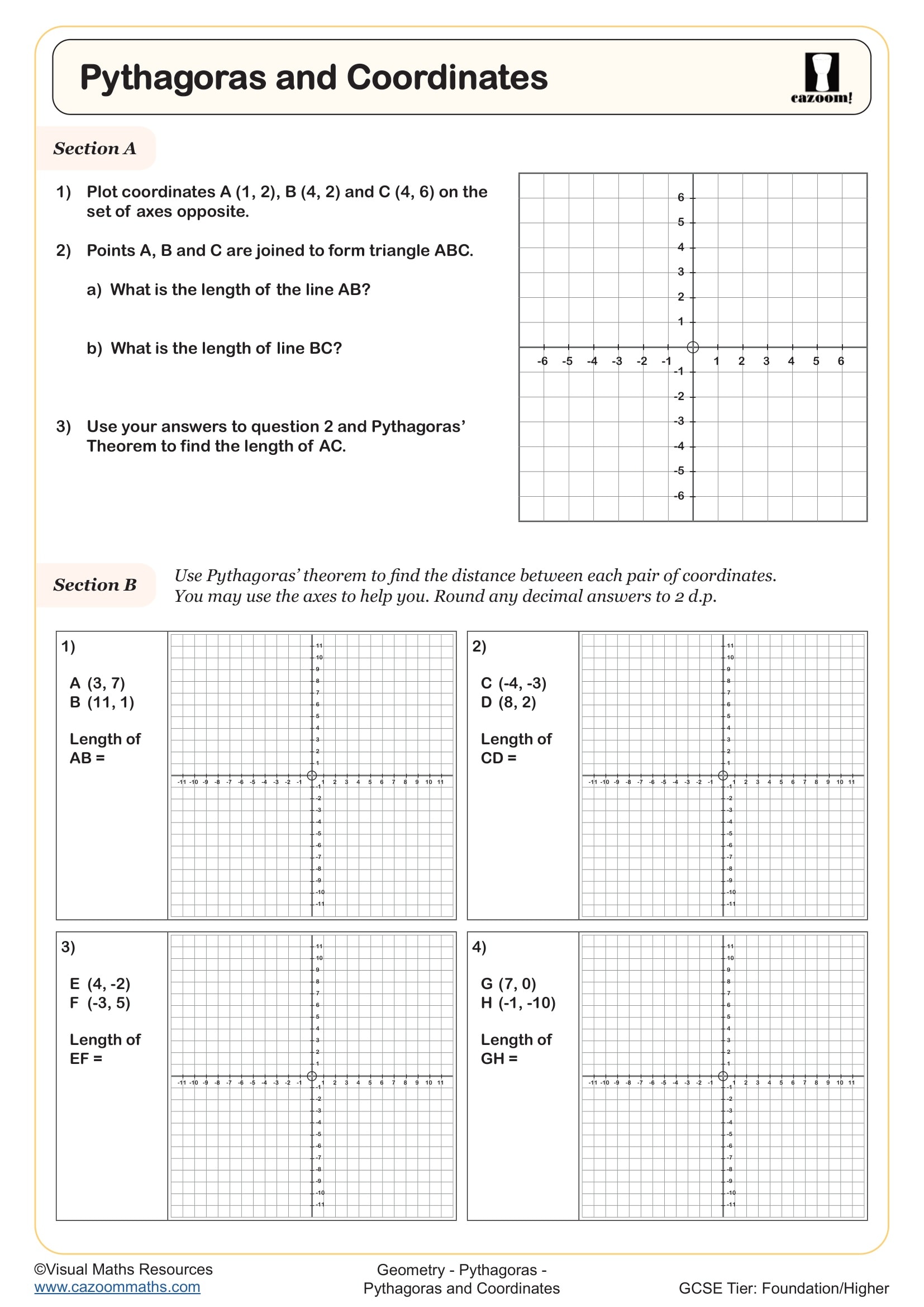
Pythagoras and Coordinates
Pythagoras Word Problems

Pythagoras Word Problems (With Clues)

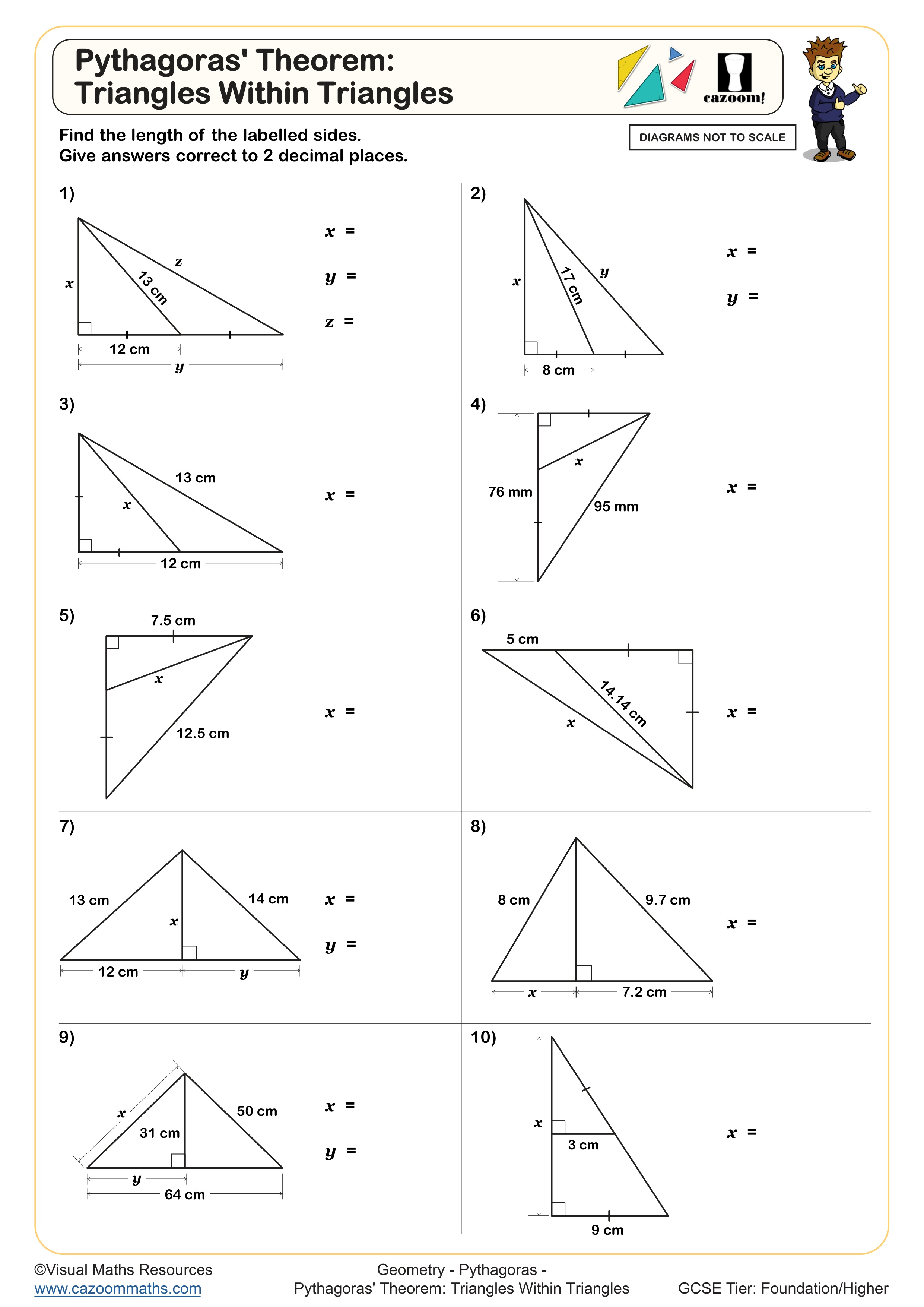
Pythagoras' Theorem: Triangles Within Triangles
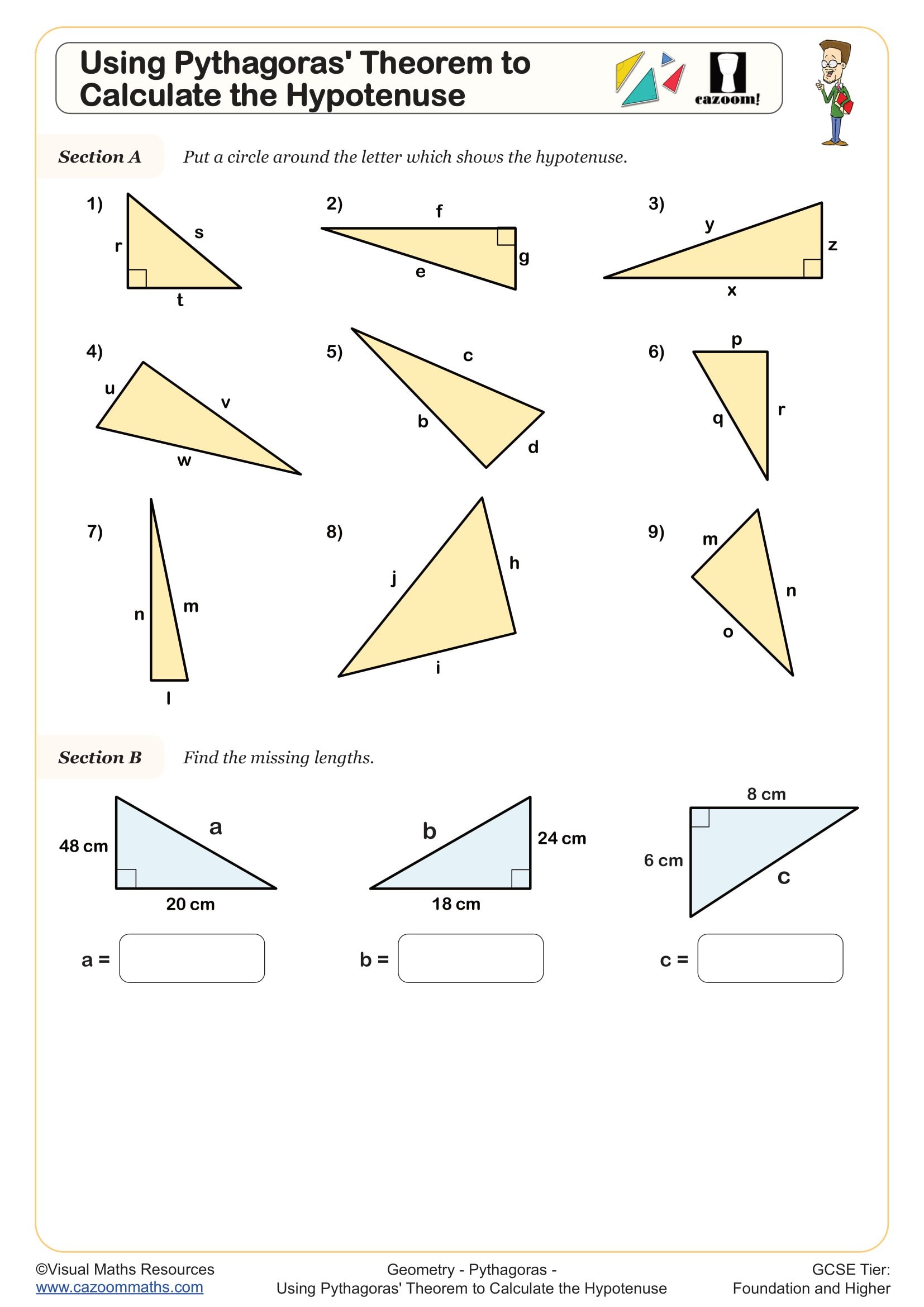
Using Pythagoras Theorem to Calculate the Hypotenuse
Using Pythagoras' Theorem to Calculate Missing Lengths in Right Angled Triangles

What is Pythagoras' theorem and why do students learn it?
Pythagoras' theorem states that in a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides (a² + b² = c²). Students meet this formally in Year 9 as part of the KS3 National Curriculum, where it appears under geometry and measures. The theorem provides the foundation for calculating distances, working with coordinates in higher dimensions, and solving problems involving diagonal measurements.
Many students lose marks in assessments by substituting values incorrectly, particularly placing a shorter side instead of the hypotenuse as 'c' in the formula. Teachers notice this error most frequently when the triangle sits on a grid at an angle or when students work backwards to find a shorter side, forgetting to subtract rather than add the squared values before taking the square root.
Which year group learns Pythagoras' theorem?
Pythagoras' theorem appears in the Year 9 curriculum, typically introduced after students have developed confidence with squares, square roots, and basic algebraic manipulation. At KS3, the National Curriculum expects students to apply the theorem to find lengths in two-dimensional shapes and progress towards problems set in coordinate geometry and three-dimensional contexts. This forms essential groundwork for GCSE, where Pythagoras appears across Foundation and Higher tiers.
The progression within Year 9 moves from straightforward calculations with integer answers through to problems requiring surds in exact form, decimal approximations, and multi-step reasoning. Students extend their understanding to find distances between coordinates, calculate diagonals within cuboids, and recognise when Pythagoras applies within composite shapes where right angles aren't immediately obvious.
How does Pythagoras' theorem connect to finding volume?
Finding volume using Pythagoras' theorem typically involves calculating an unknown dimension needed for the volume formula itself. For example, students might need to find the perpendicular height of a triangular prism by first using Pythagoras to determine the height of the triangular cross-section, then applying volume = area of cross-section × length. Similarly, problems involving pyramids or cones may require Pythagoras to calculate slant heights or base dimensions before volume calculations proceed.
This skill appears regularly in construction and engineering contexts, where professionals calculate material quantities for sloped structures. Architects use Pythagoras to determine roof volumes when specifying insulation materials, whilst structural engineers apply the theorem to calculate capacities of triangulated frameworks. These real-world applications demonstrate why understanding both geometric relationships and volume calculations together matters beyond examinations, particularly in STEM careers where spatial reasoning underpins technical problem-solving.
How can teachers use these Pythagoras worksheets effectively?
The worksheets build systematic practice through carefully structured questions that isolate specific skills before combining them. Starting with basic applications allows students to automate the substitution process, whilst later questions involving surds and coordinates challenge those ready to work at greater depth. The included answer sheets enable students to self-check their working, identifying where errors occur in their calculation process rather than just whether their final answer matches.
Teachers find these resources particularly useful for intervention sessions where small groups work through common errors with targeted support. The worksheets also work well as homework tasks following initial teaching, allowing students to consolidate methods independently before moving to more complex applications. For revision purposes, the range of subtopics means students can focus on specific areas of weakness, whilst the embedded triangles and coordinate problems provide stretch for early finishers during mixed-ability lessons.