KS3 Volume and Surface Area Worksheets
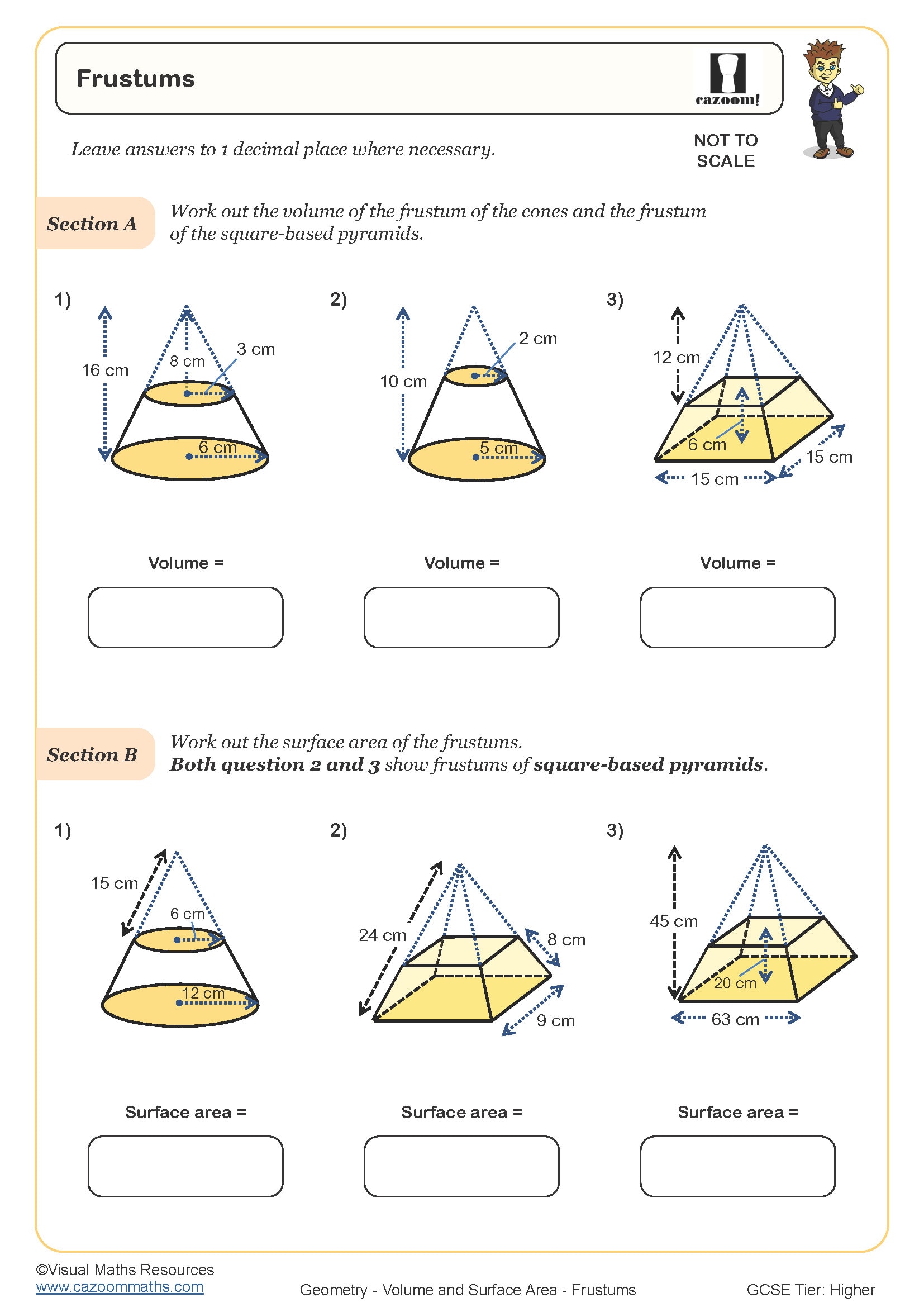
Frustums
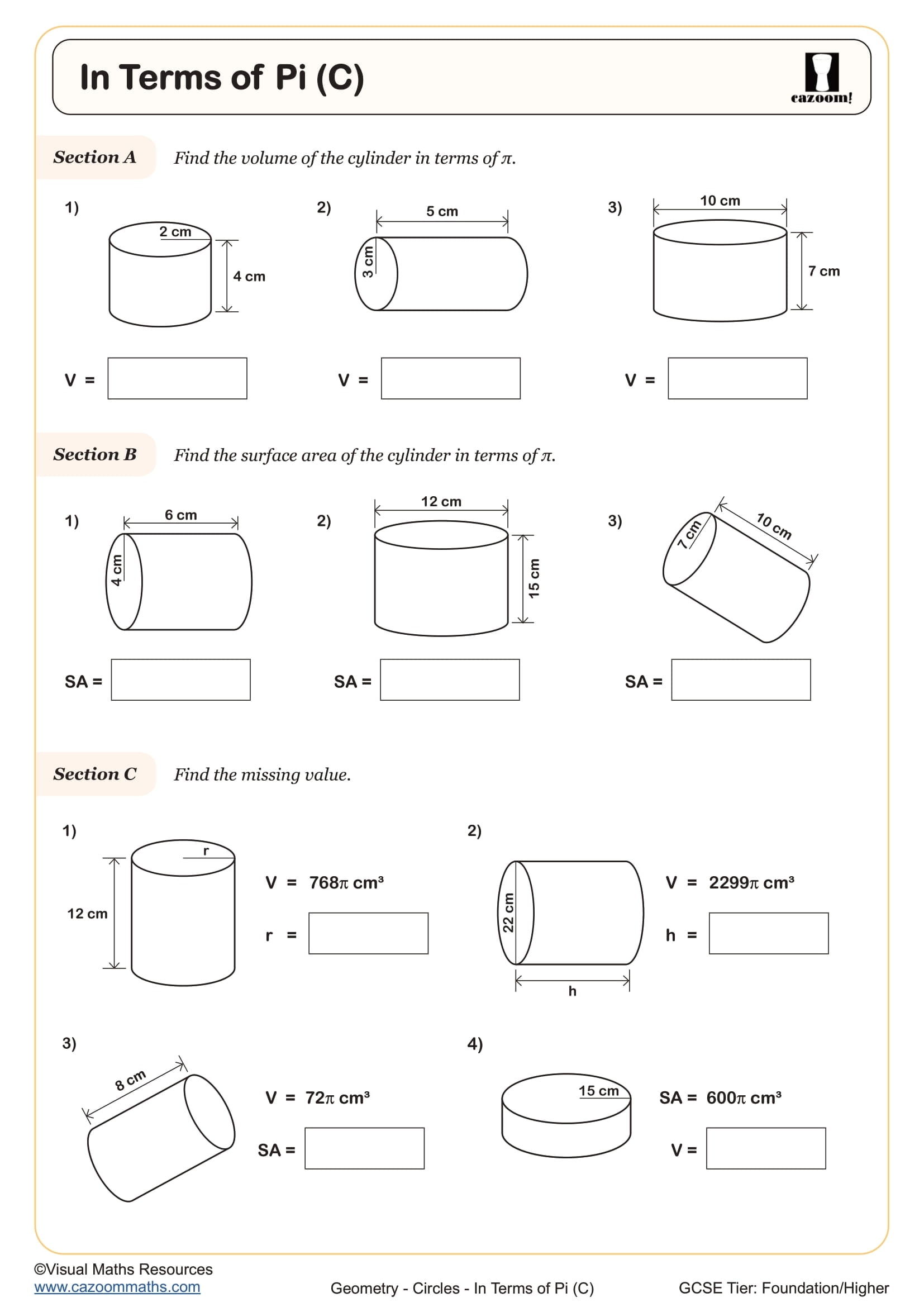
In Terms of Pi (C)
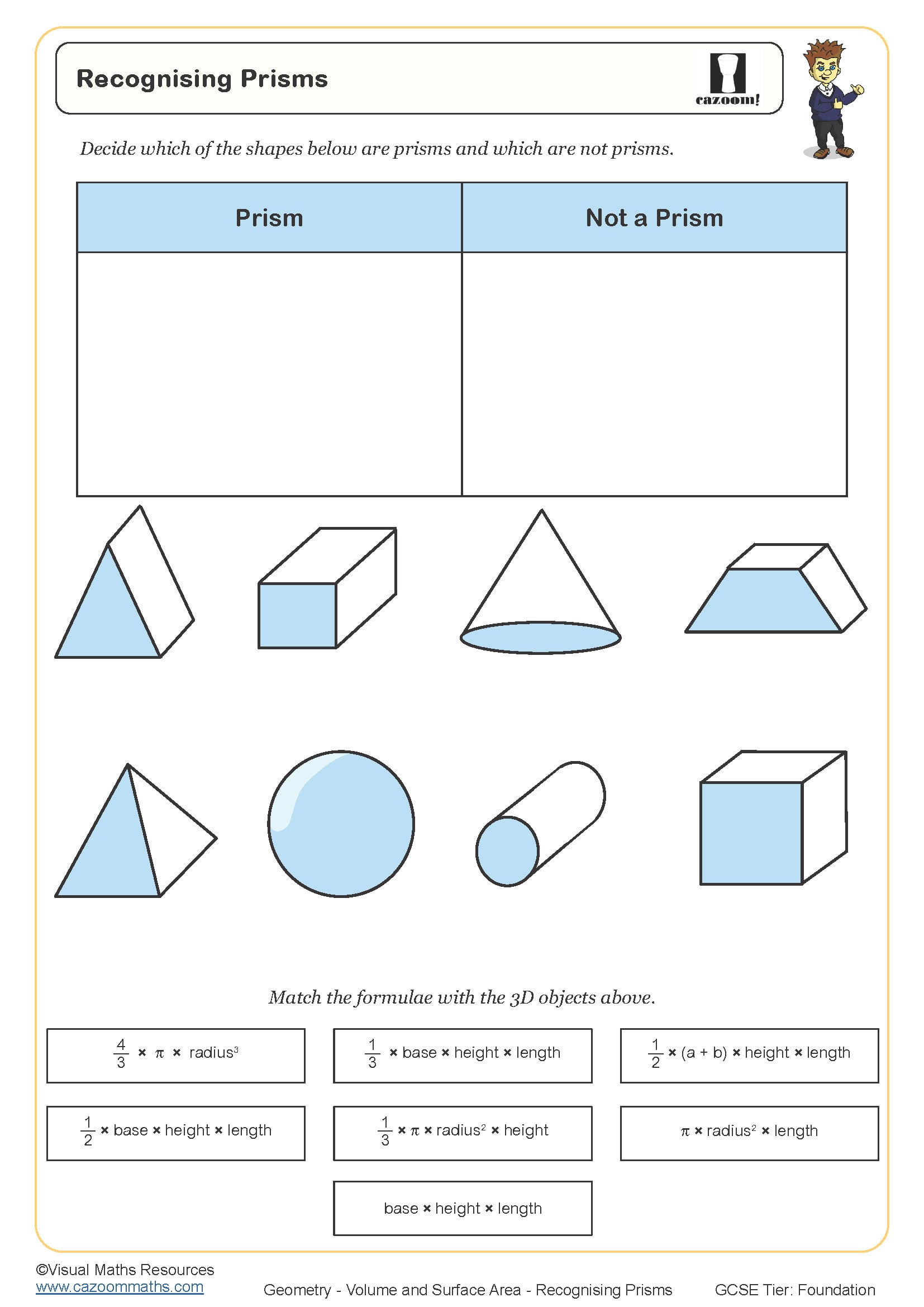
Recognising Prisms
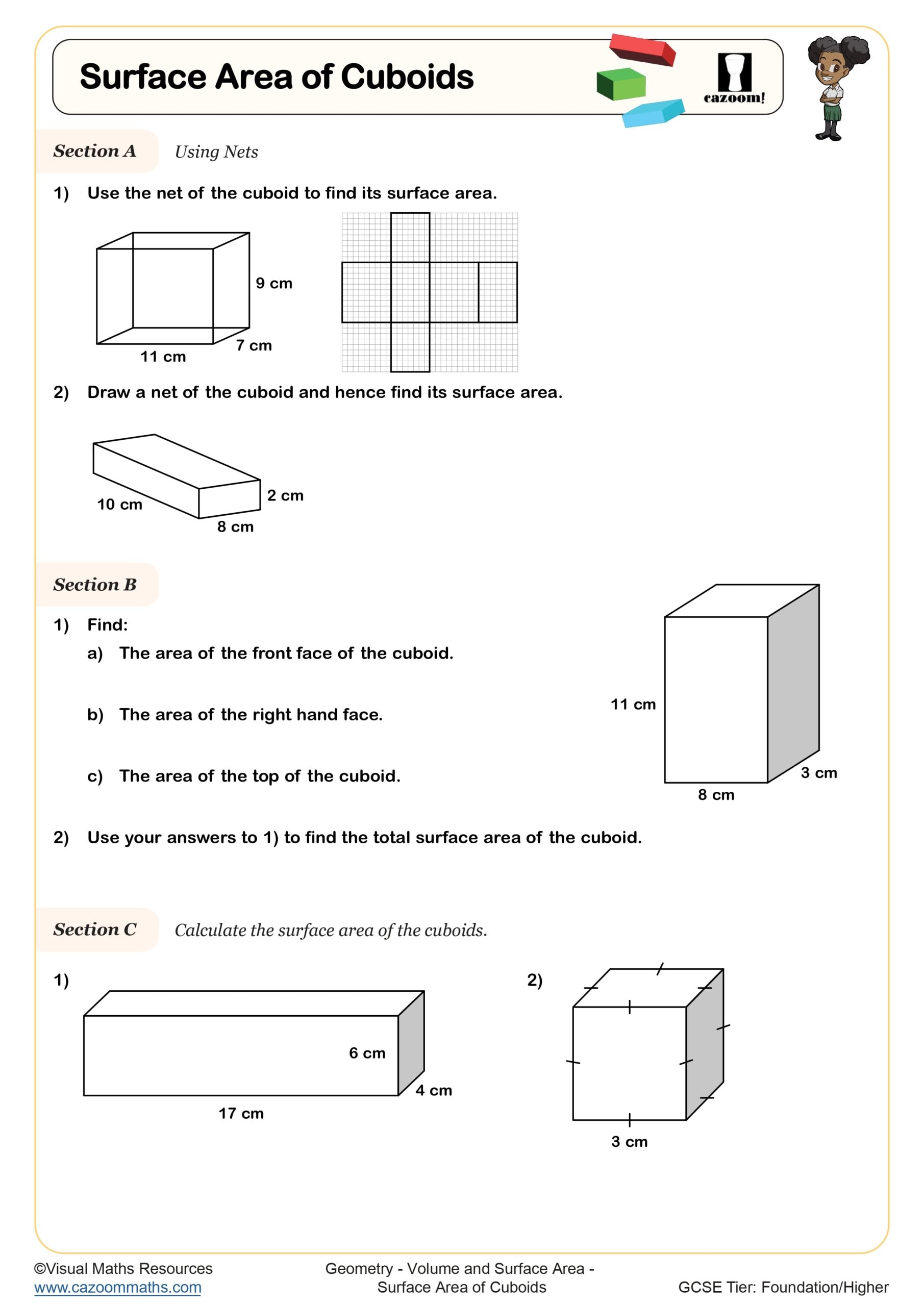
Surface Area of Cuboids
Surface Area of Cylinders
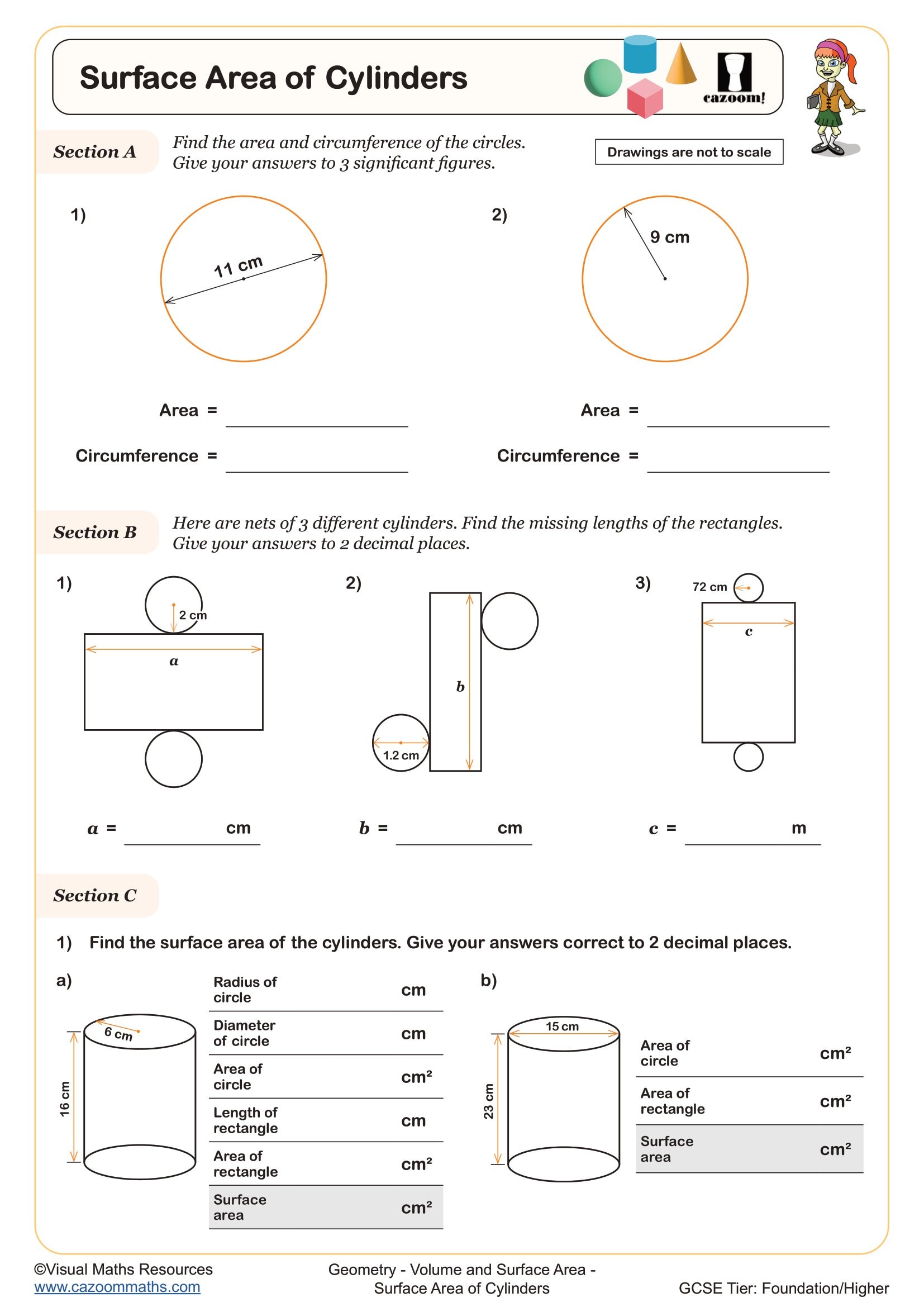
Surface Area of Prisms
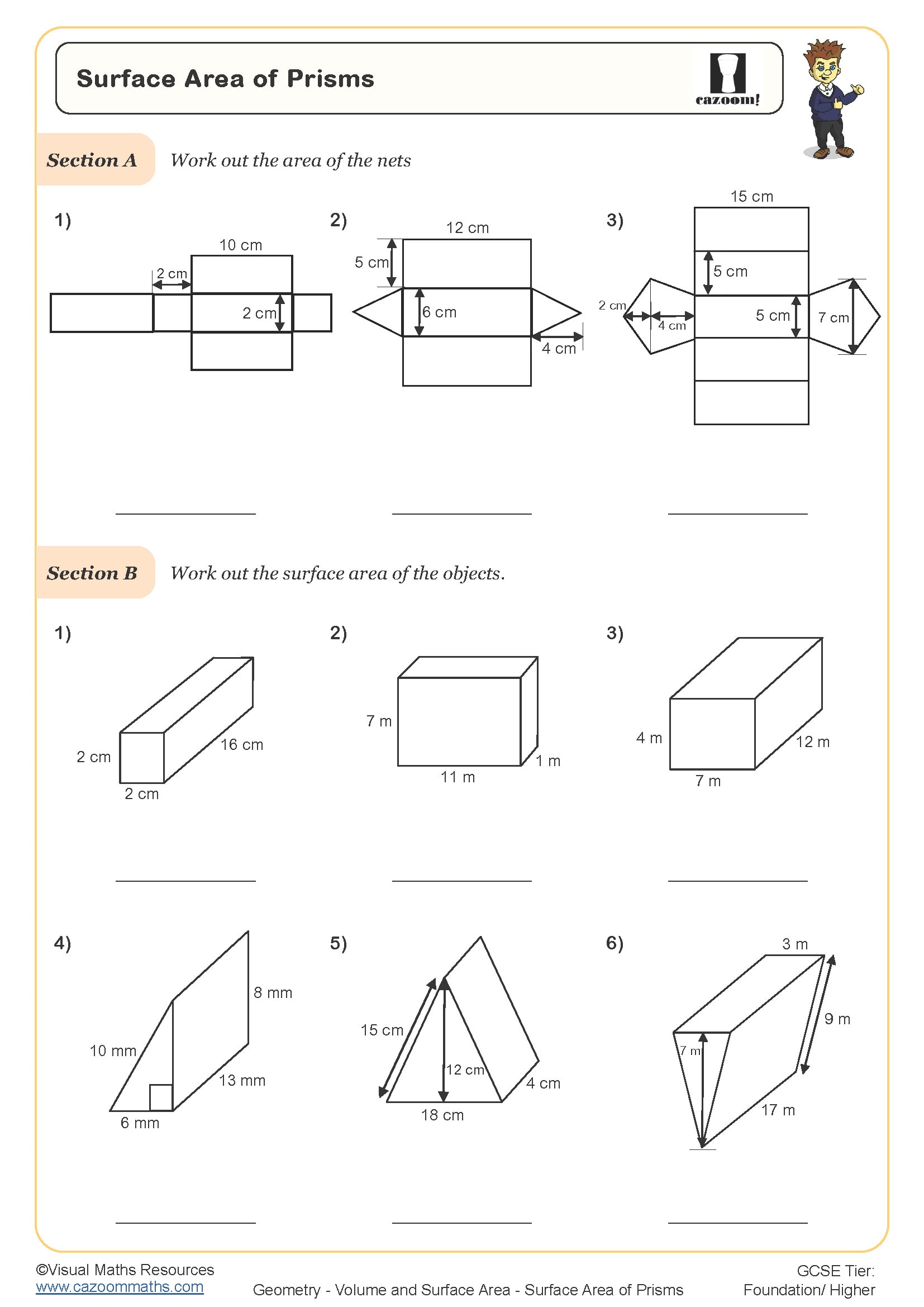
Surface Area of Triangular Prisms
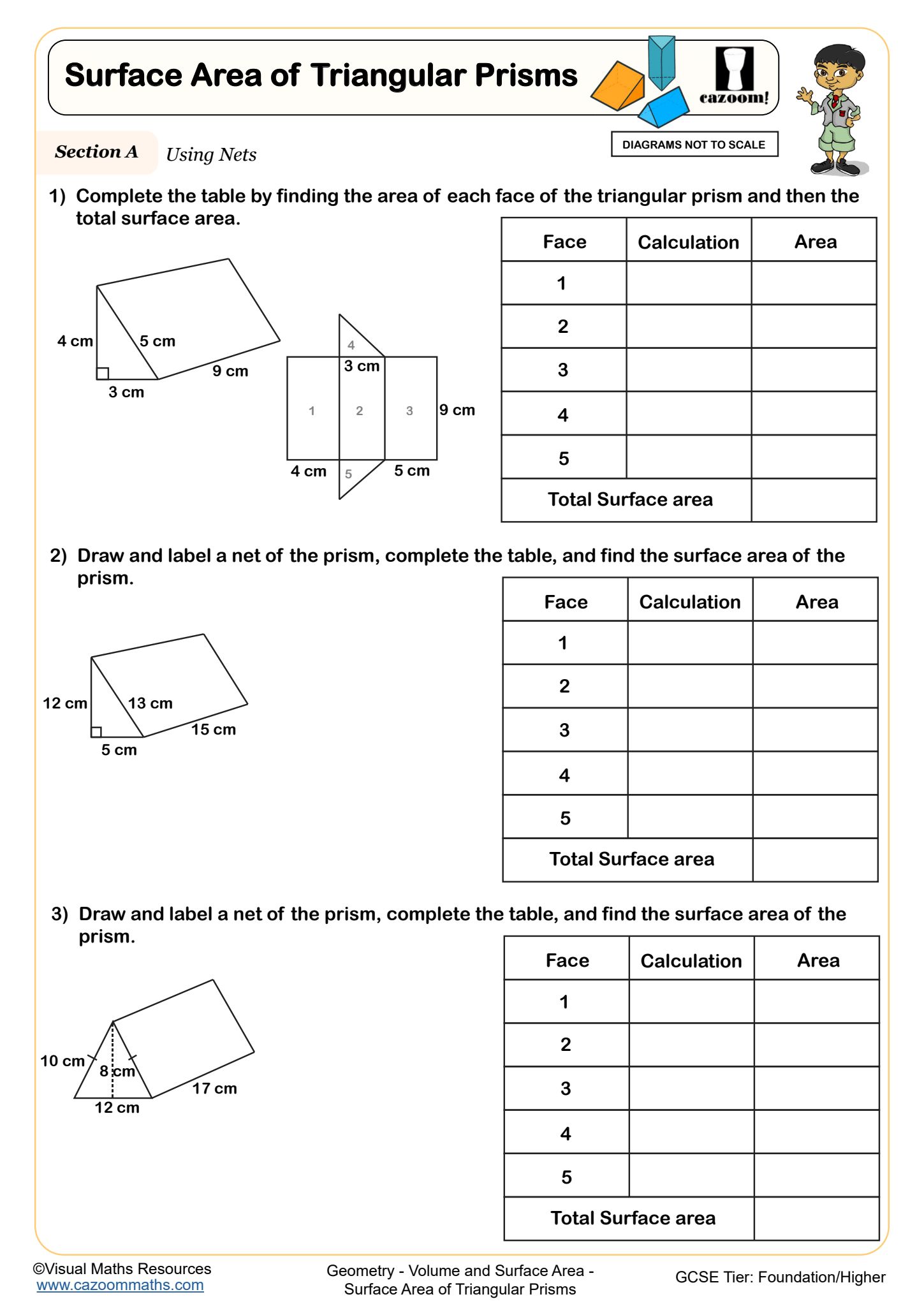
Surface Area- 'L' Shaped Prisms
Volume and Surface Area of Cuboids
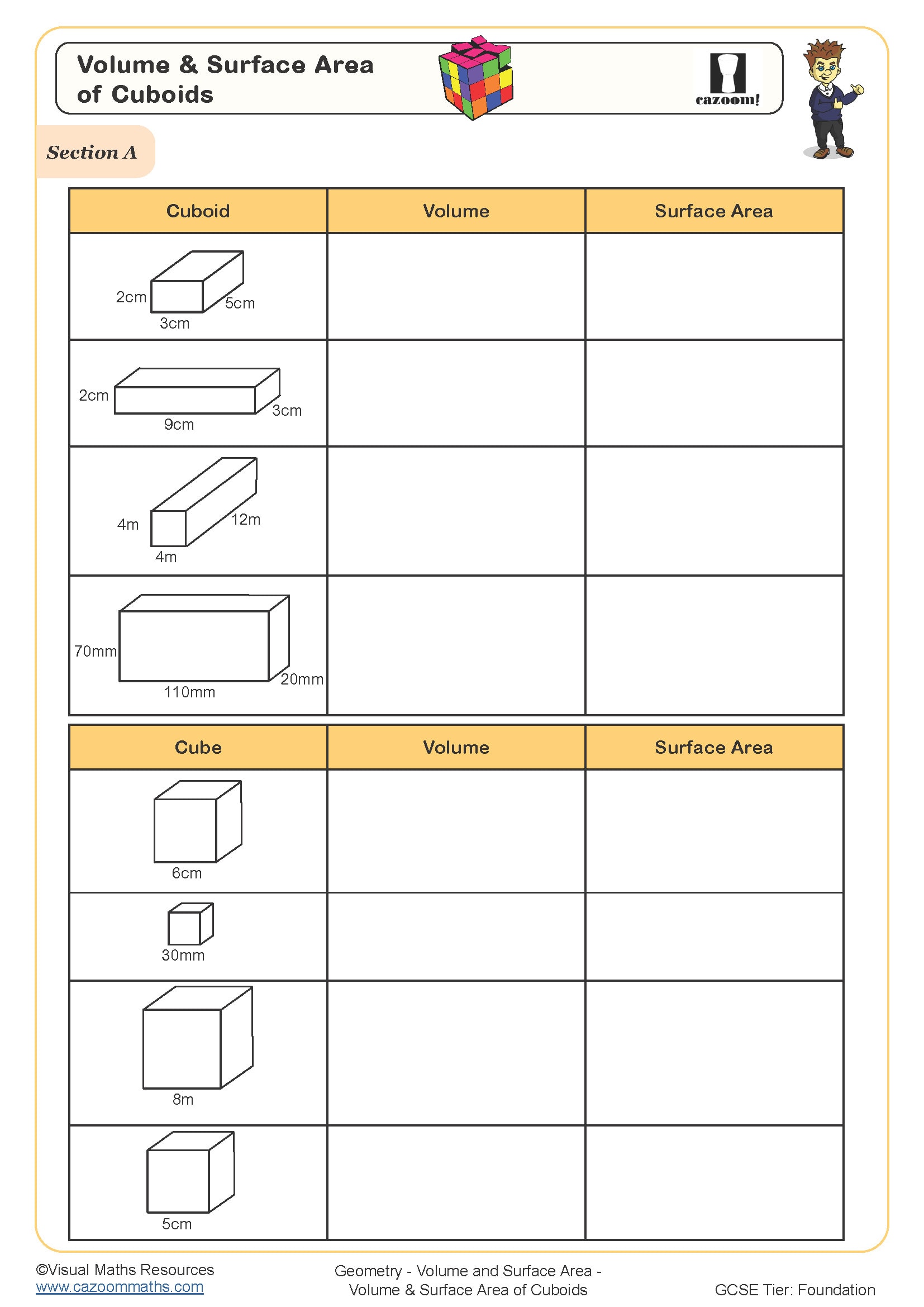
Volume of a Cylinder
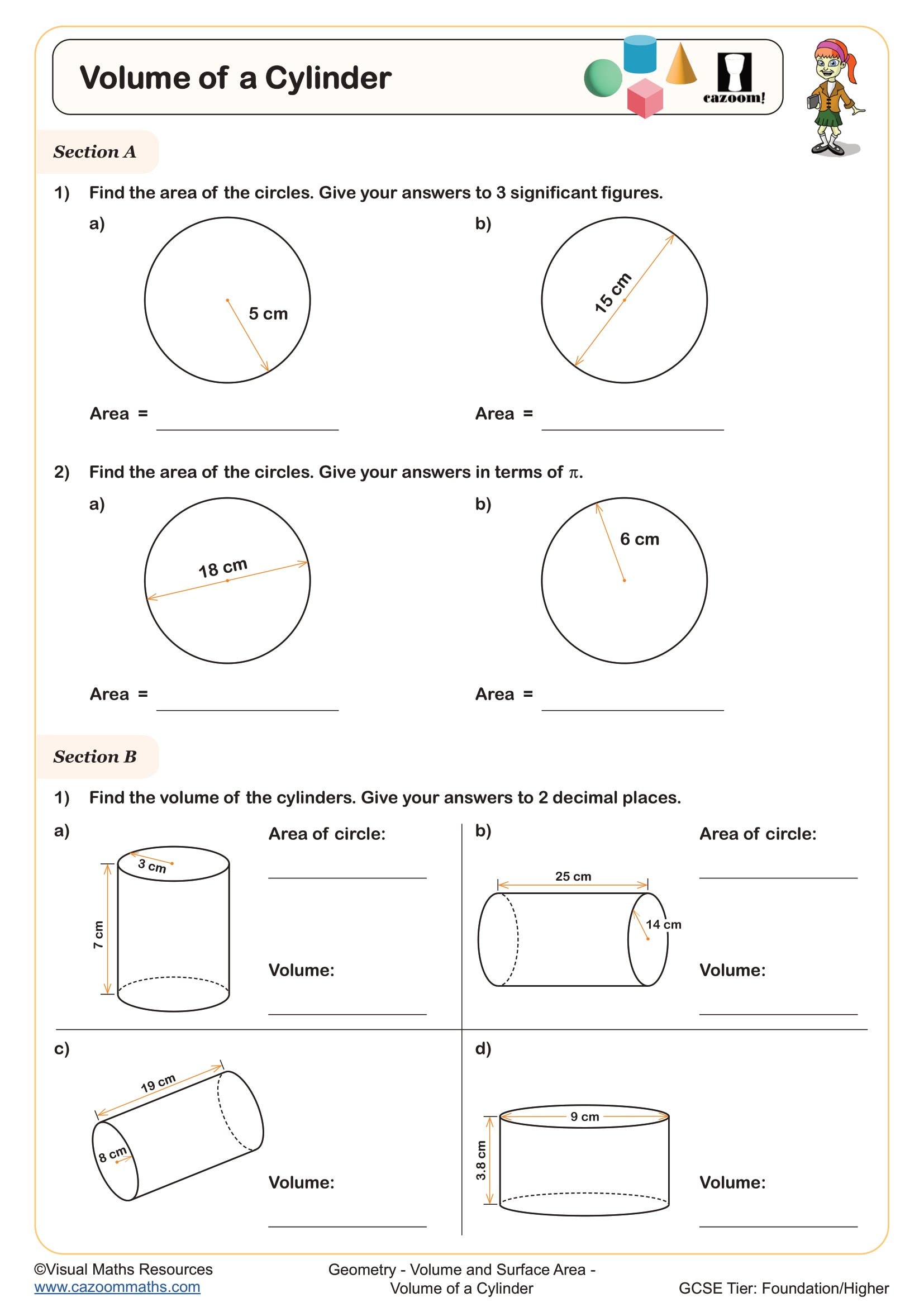
Volume of Compound 3D shapes
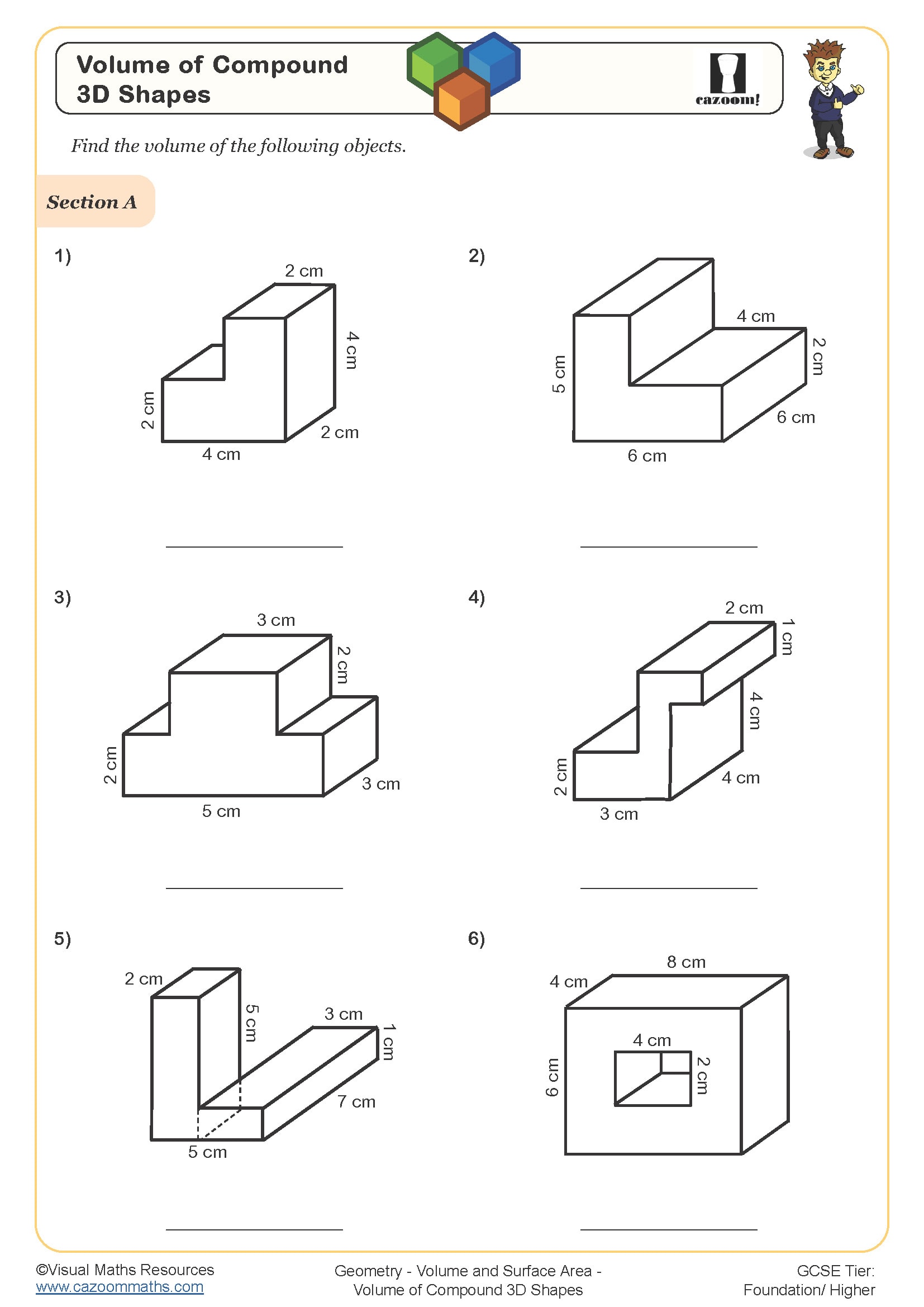
Volume of Cuboids
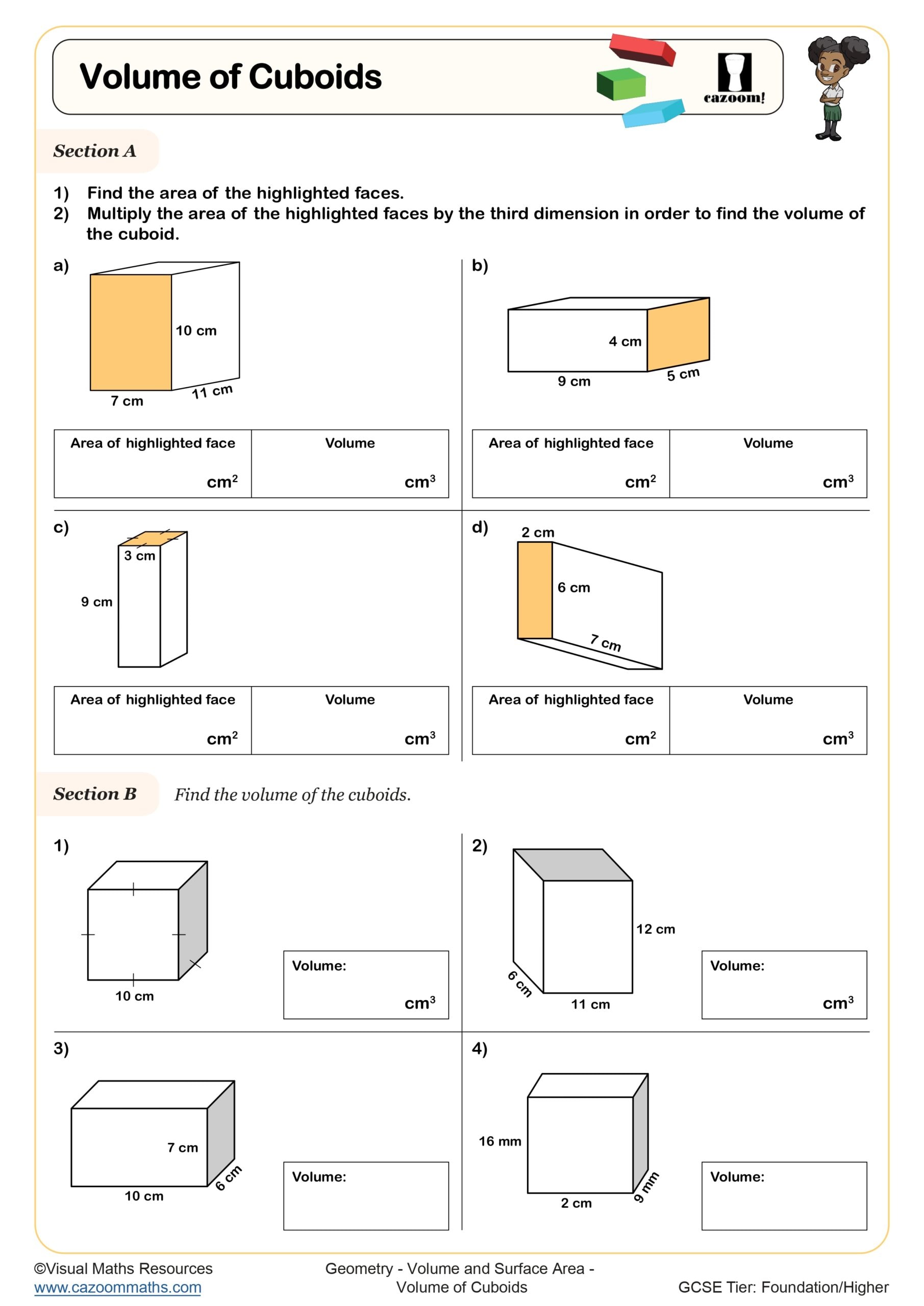
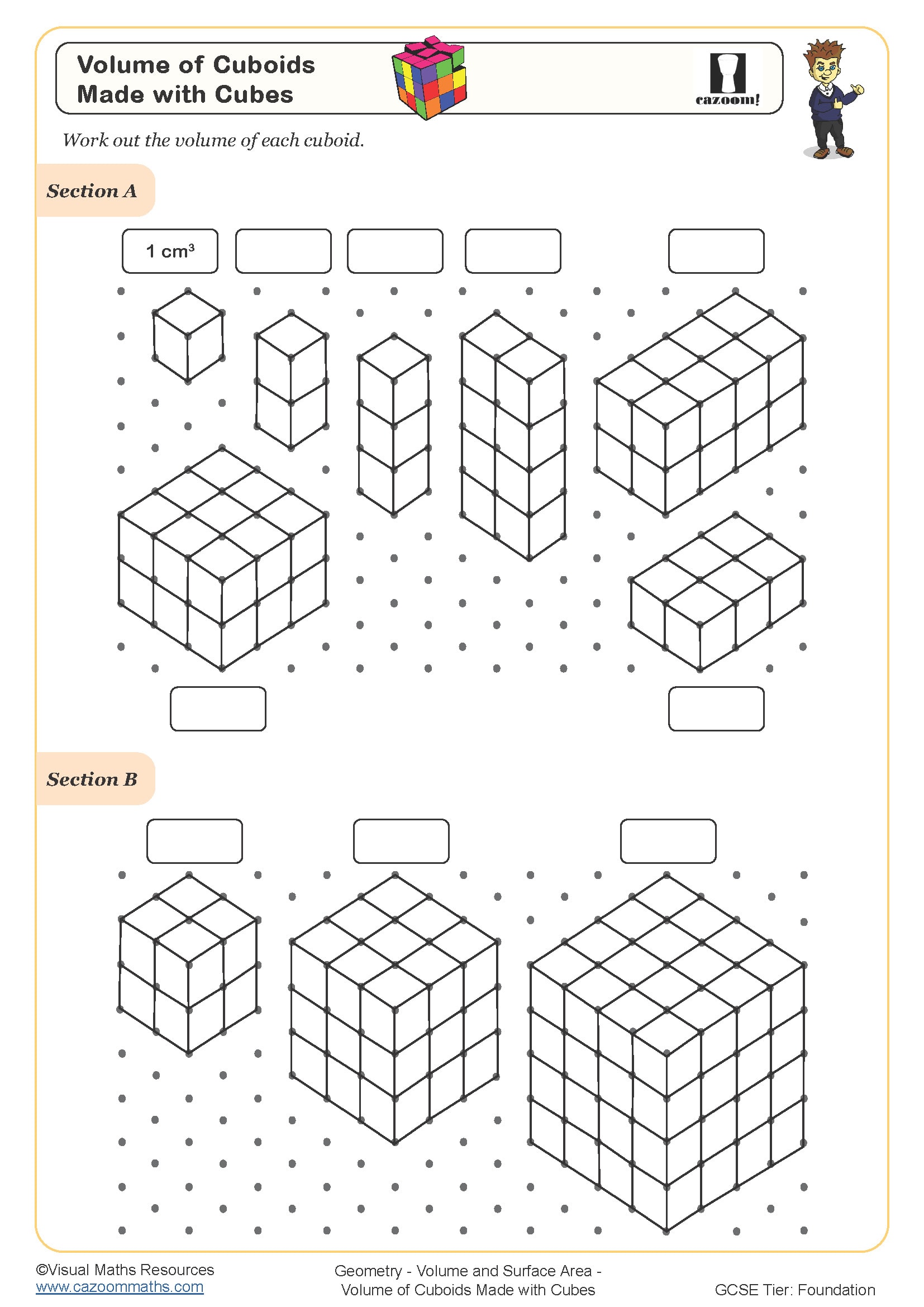
Volume of Cuboids made with Cubes
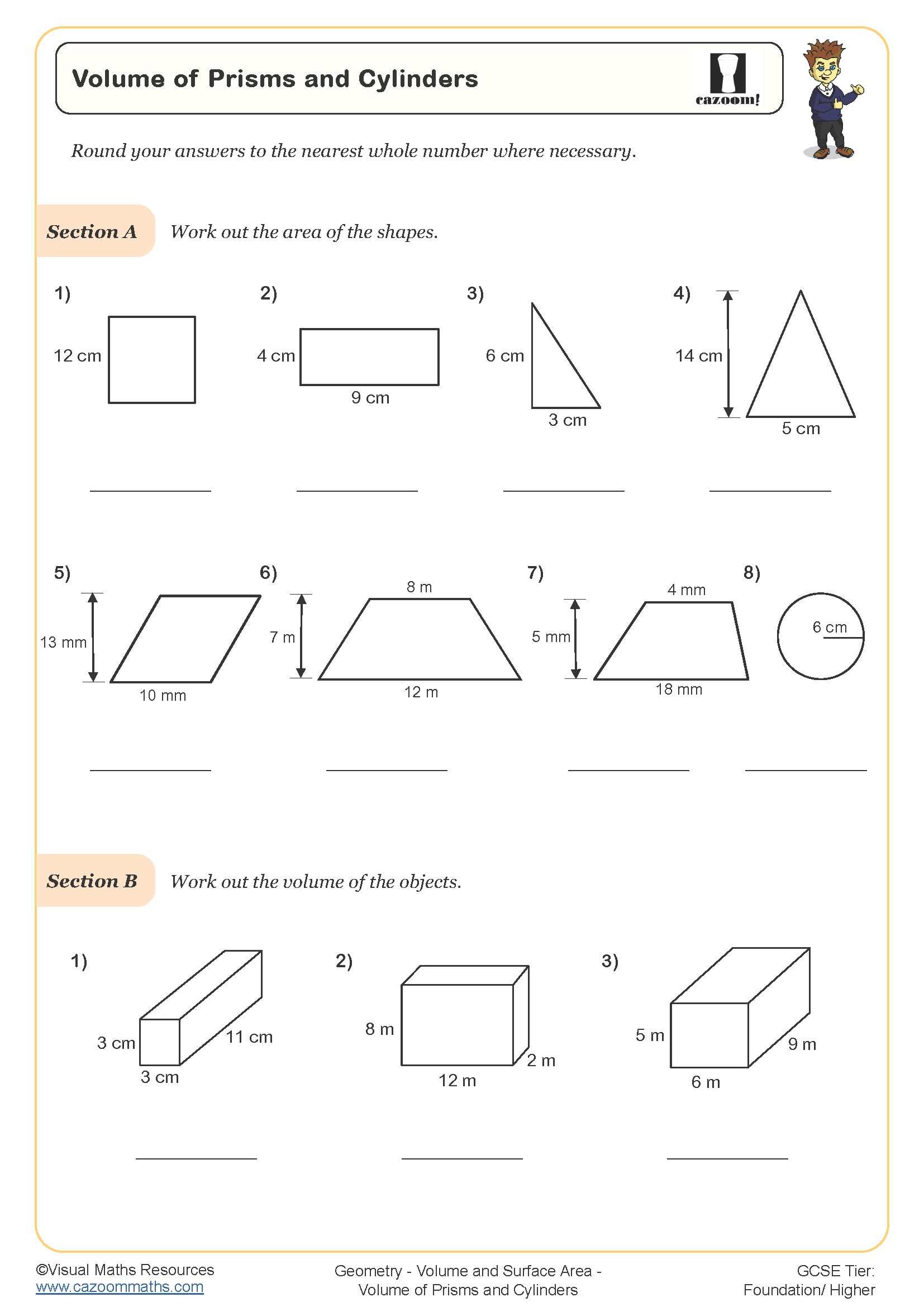
Volume of Prisms and Cylinders
Volume Word Problems

What types of volume of shapes worksheet are included?
The worksheets cover the key 3D shapes required at KS3: cubes, cuboids, prisms (including triangular and trapezoidal), pyramids, cylinders, cones, and spheres. Students work with volume formulae, surface area calculations, and problems involving composite shapes made from combining these solids. Questions progress from straightforward single-shape calculations to more demanding multi-step problems that require converting units or working backwards from a given volume.
Teachers frequently notice that students can apply formulae mechanically but struggle when questions change format, such as finding a missing dimension when the volume is given. The worksheets address this by including varied question styles, helping students recognise when to rearrange formulae and check their answers make sense in context.
Which year groups are these worksheets suitable for?
These worksheets are designed for Year 7, Year 8, and Year 9 students following the KS3 National Curriculum. Volume and surface area first appears in Year 7 with simple prisms and cuboids, where students learn to apply formulae confidently. The topic builds throughout KS3 as students encounter more complex shapes and compound solids.
Progression across the year groups involves moving from shapes with clear right angles and simple dimensions to pyramids with slant heights, spheres requiring π, and composite solids where students must identify which parts to calculate separately. By Year 9, students should handle problems involving algebraic expressions for dimensions and connect volume calculations to real-world contexts like capacity and material costs, providing essential foundation work for GCSE.
How do students approach surface area of pyramids?
Surface area of pyramids requires students to calculate the base area separately from the triangular faces, then add these components together. For a square-based pyramid, this means finding the area of one square and four identical triangles. Students need to identify the slant height (not the perpendicular height) to calculate the triangular face area, which is where many make errors.
This skill connects directly to architecture and structural engineering, where surface area calculations determine material quantities for roofing, cladding, and waterproofing. The Louvre pyramid in Paris, for example, required precise surface area calculations to determine the amount of glass and metal framing needed. Understanding these calculations helps students appreciate how mathematics underpins construction projects, from estimating paint coverage to calculating heat loss through external surfaces in building design.
How can these worksheets support classroom teaching?
The worksheets provide structured practice that allows students to consolidate formula application and develop fluency with calculations involving 3D shapes. Each resource includes worked examples or clear formula reminders at the start, helping students who need scaffolding before attempting independent questions. The progression within each worksheet moves from straightforward calculations to more challenging problems, allowing differentiation within a single class.
Many teachers use these resources for targeted intervention with students who struggle to visualise 3D shapes or mix up volume and surface area formulae. They work well as homework following initial teaching, or as revision material before assessments. The answer sheets enable students to self-mark and identify specific areas of difficulty, making them valuable for independent study sessions or paired work where students explain their methods to each other.