KS4 Circles Worksheets
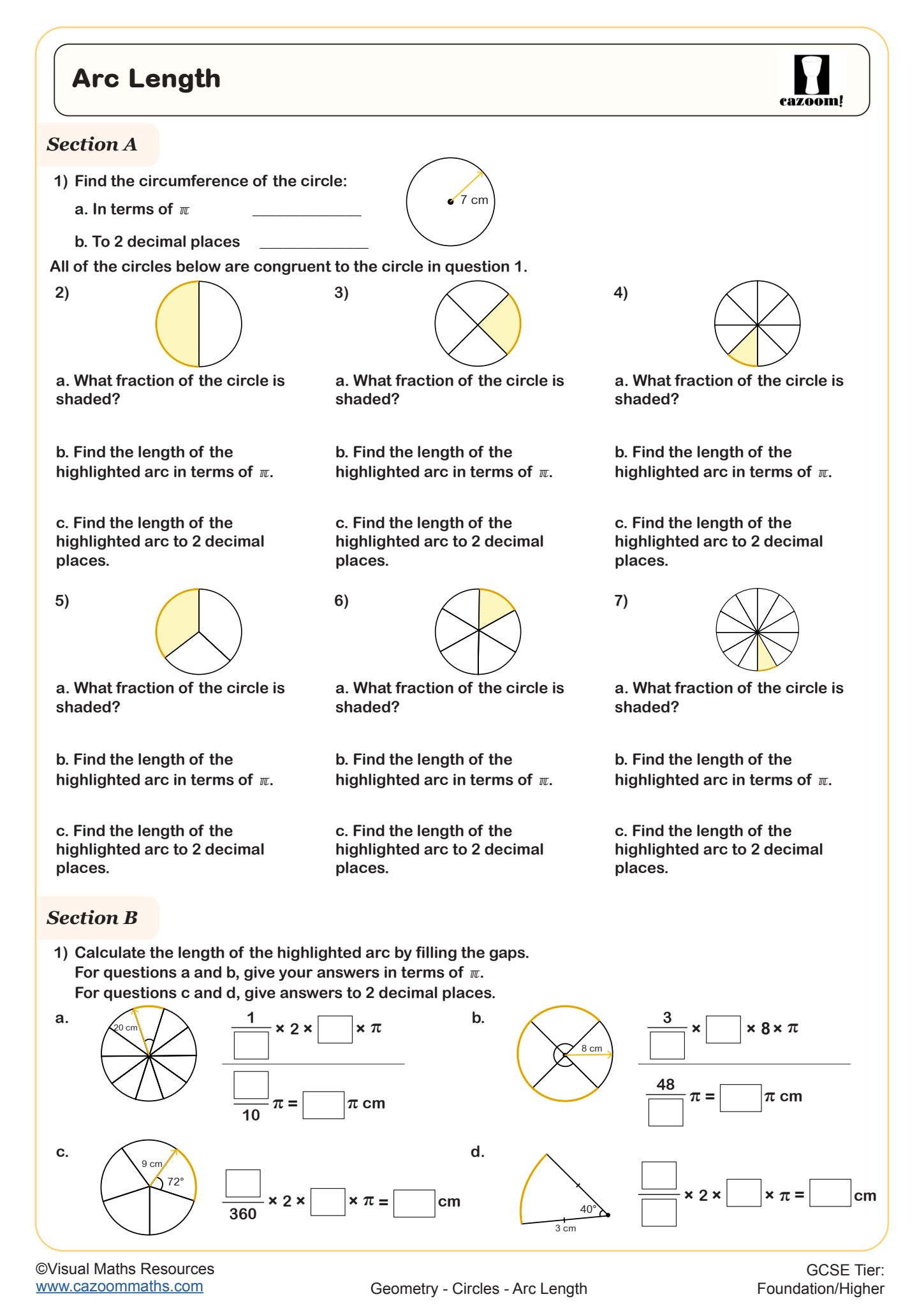
Arc Length
Area of a Sector

Area of Sectors and Arc Lengths

Area of Sectors and Segments
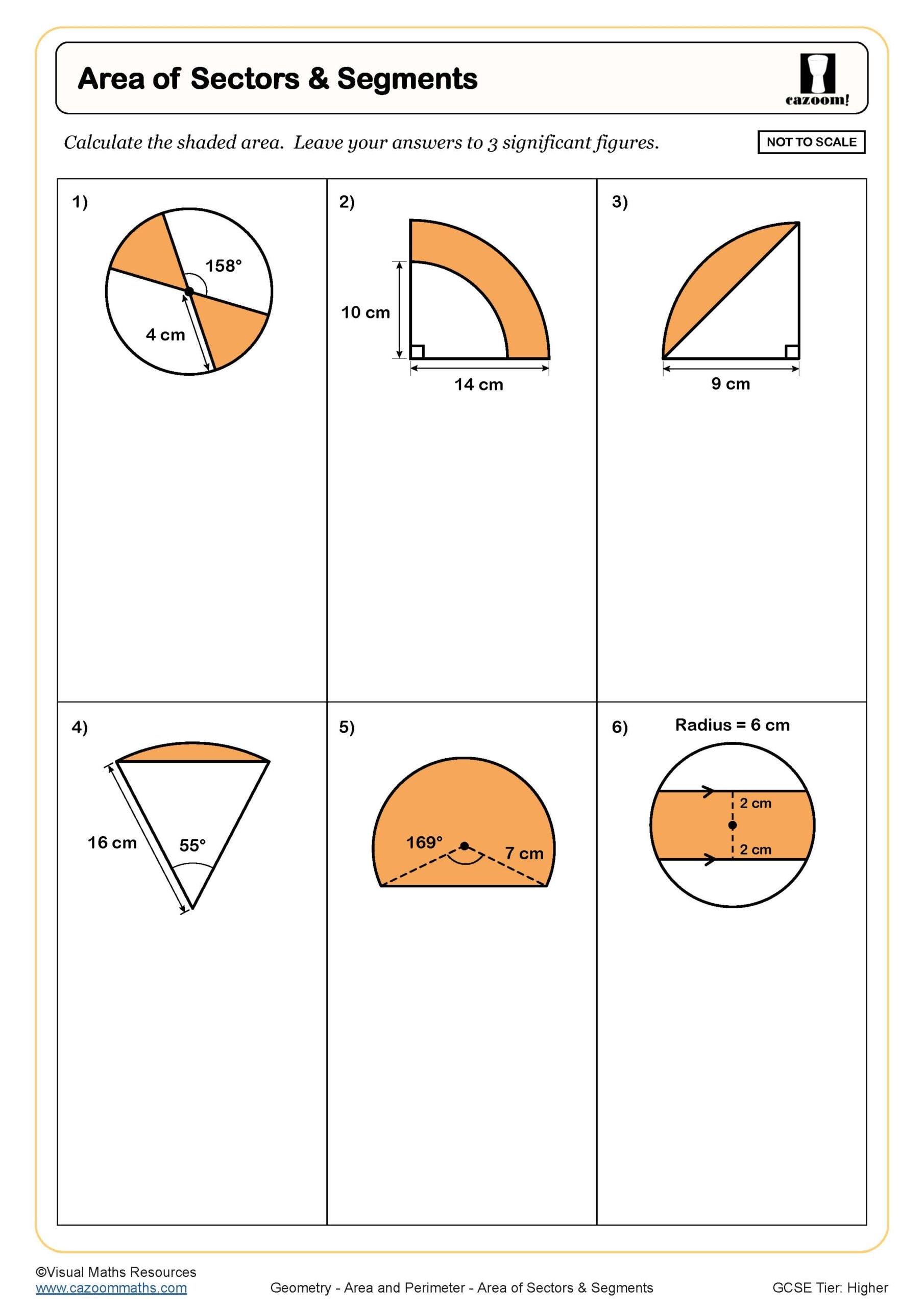
Area of Sectors and Segments (With Clues)
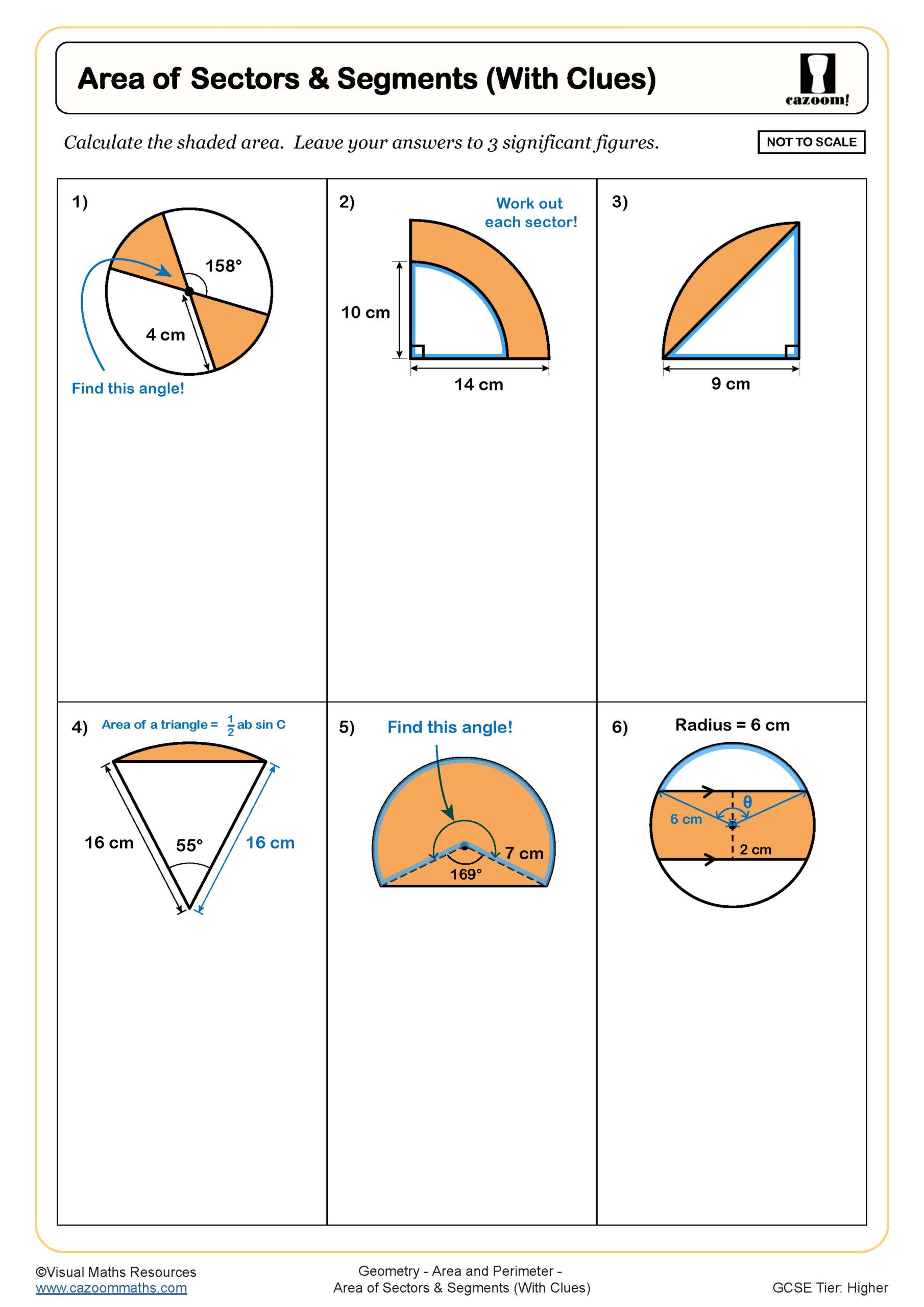
Circle Theorems (A)
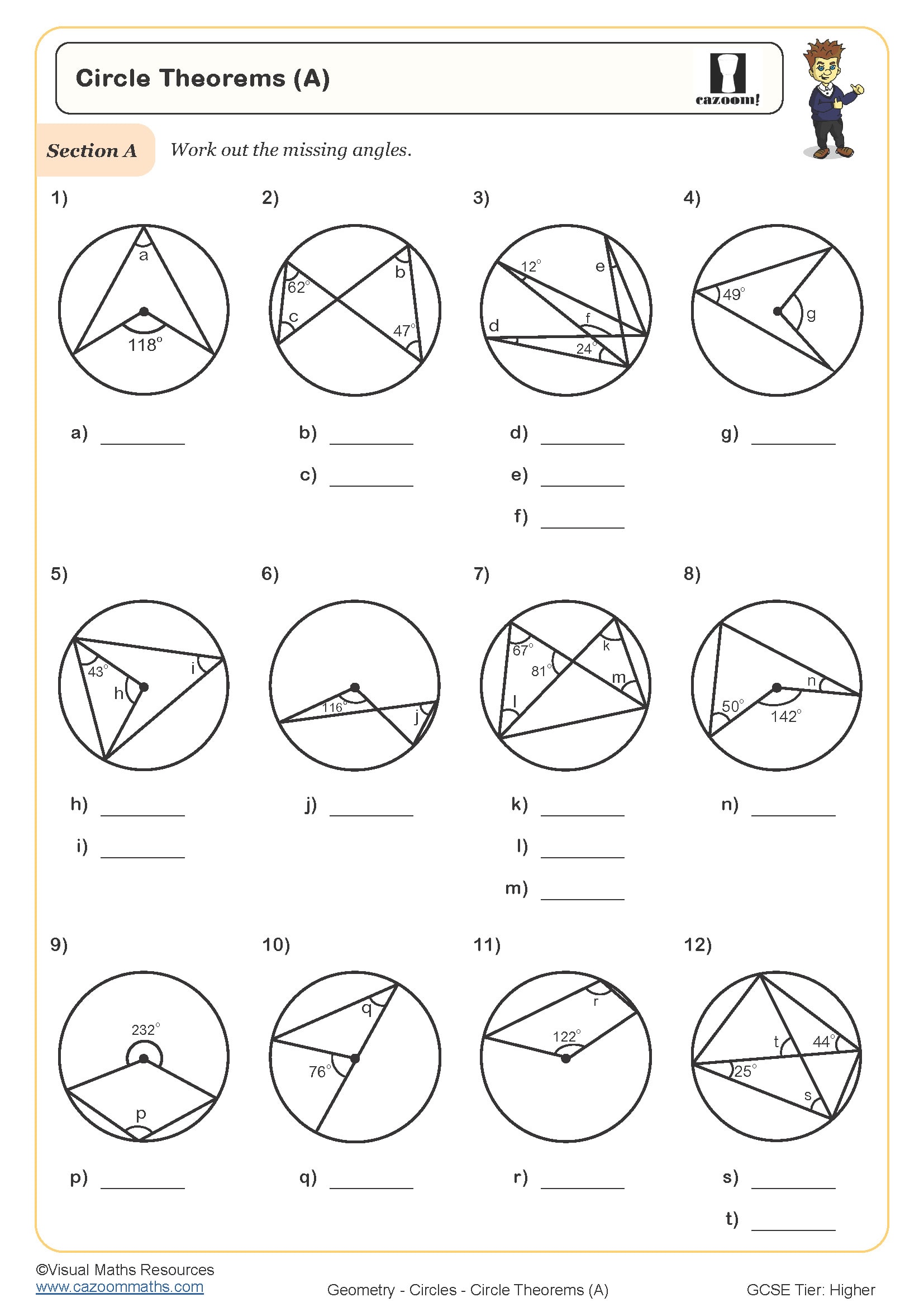
Circle Theorems (B)
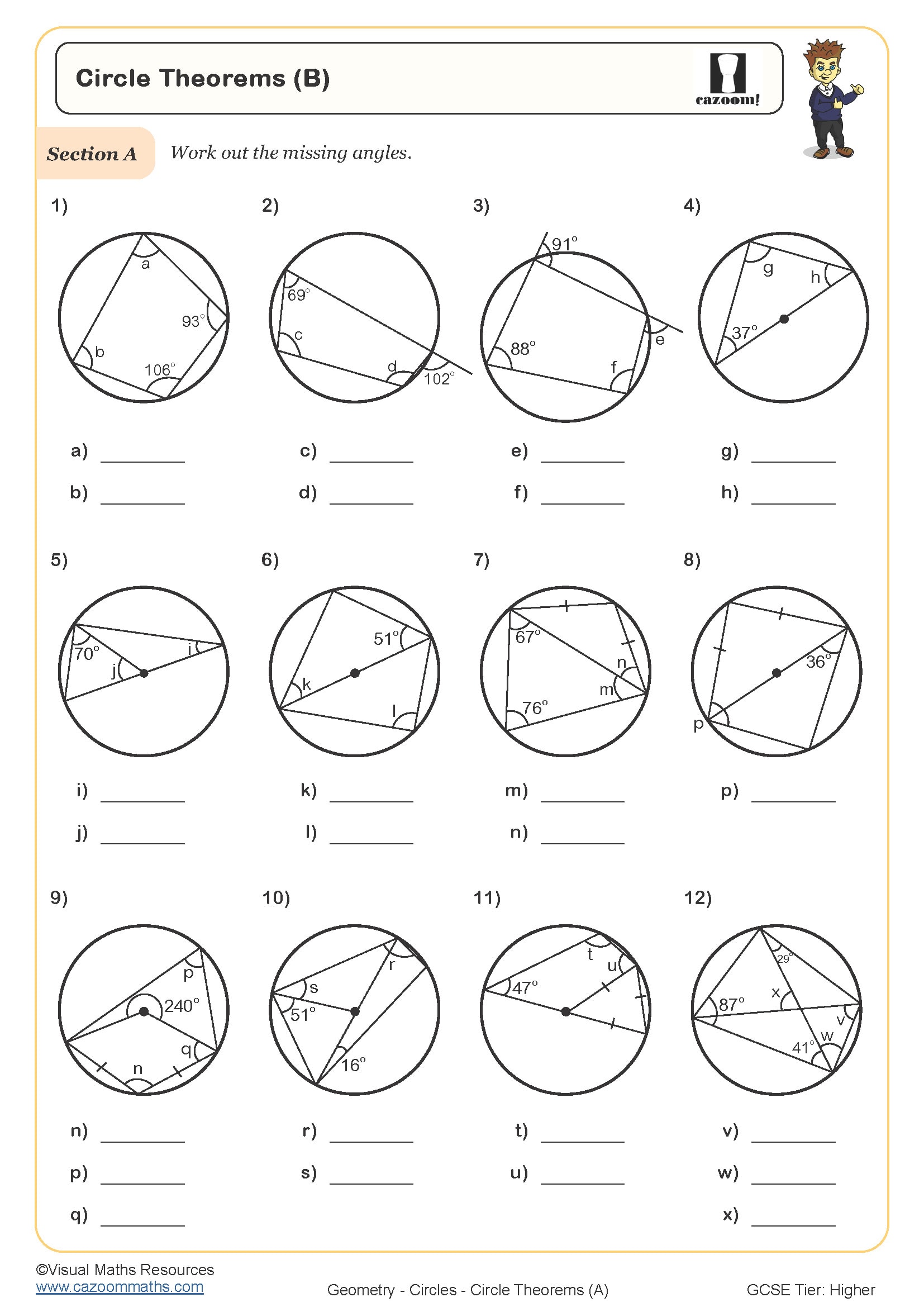
Circle Theorems (C)
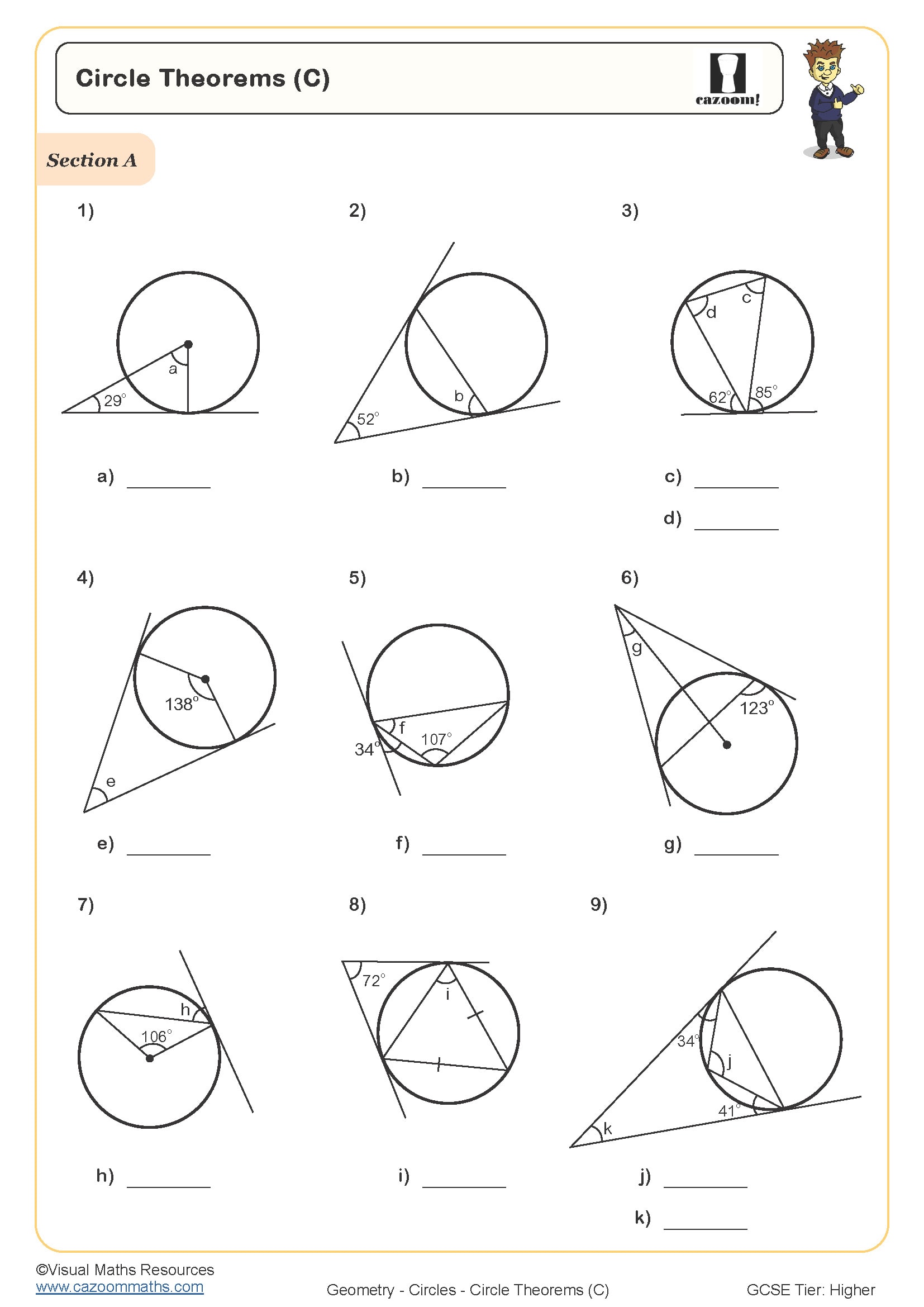
Circle Theorems: Angle at Center Twice the Angle at Circumference
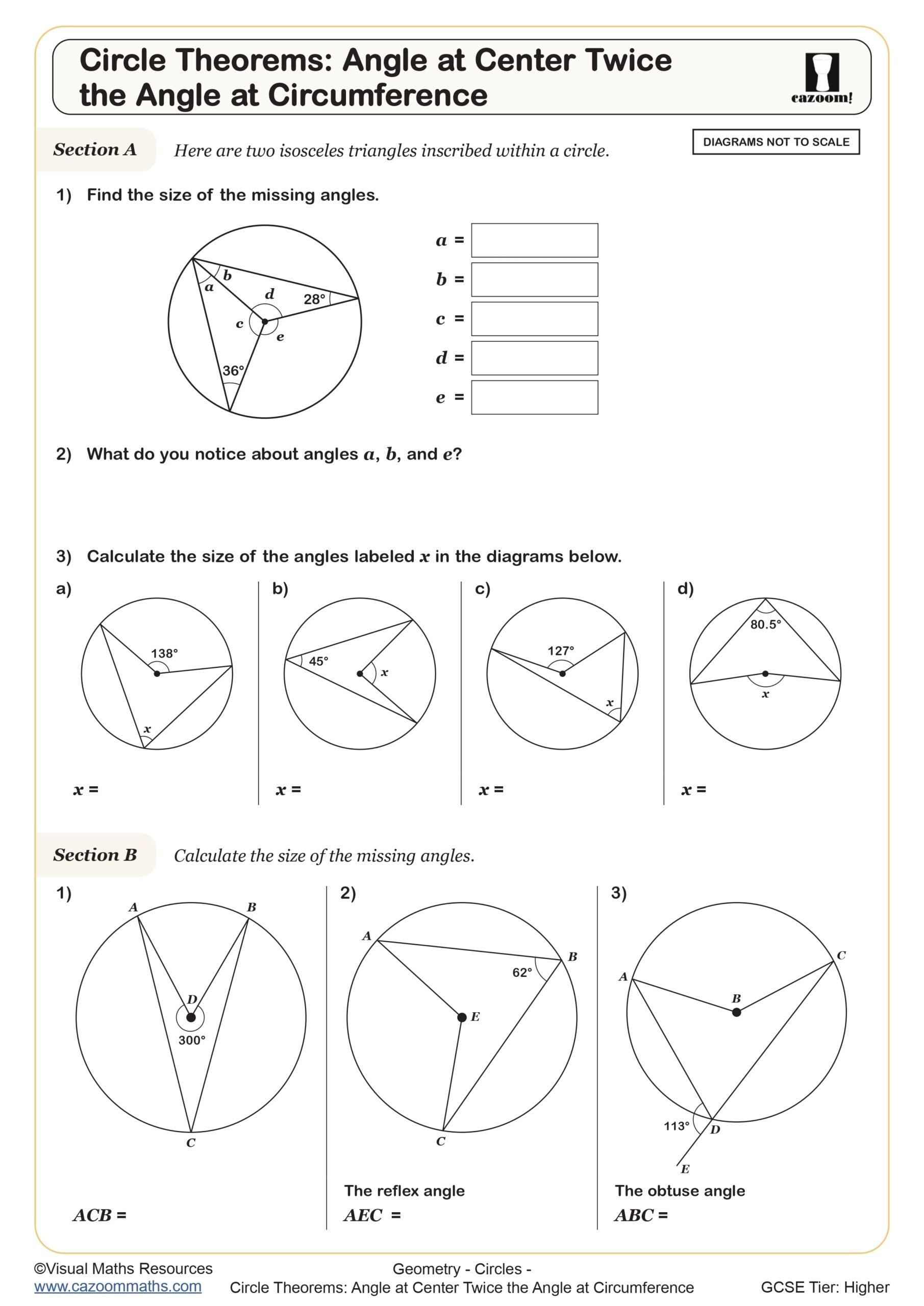
Circle Theorems: Angle Notation
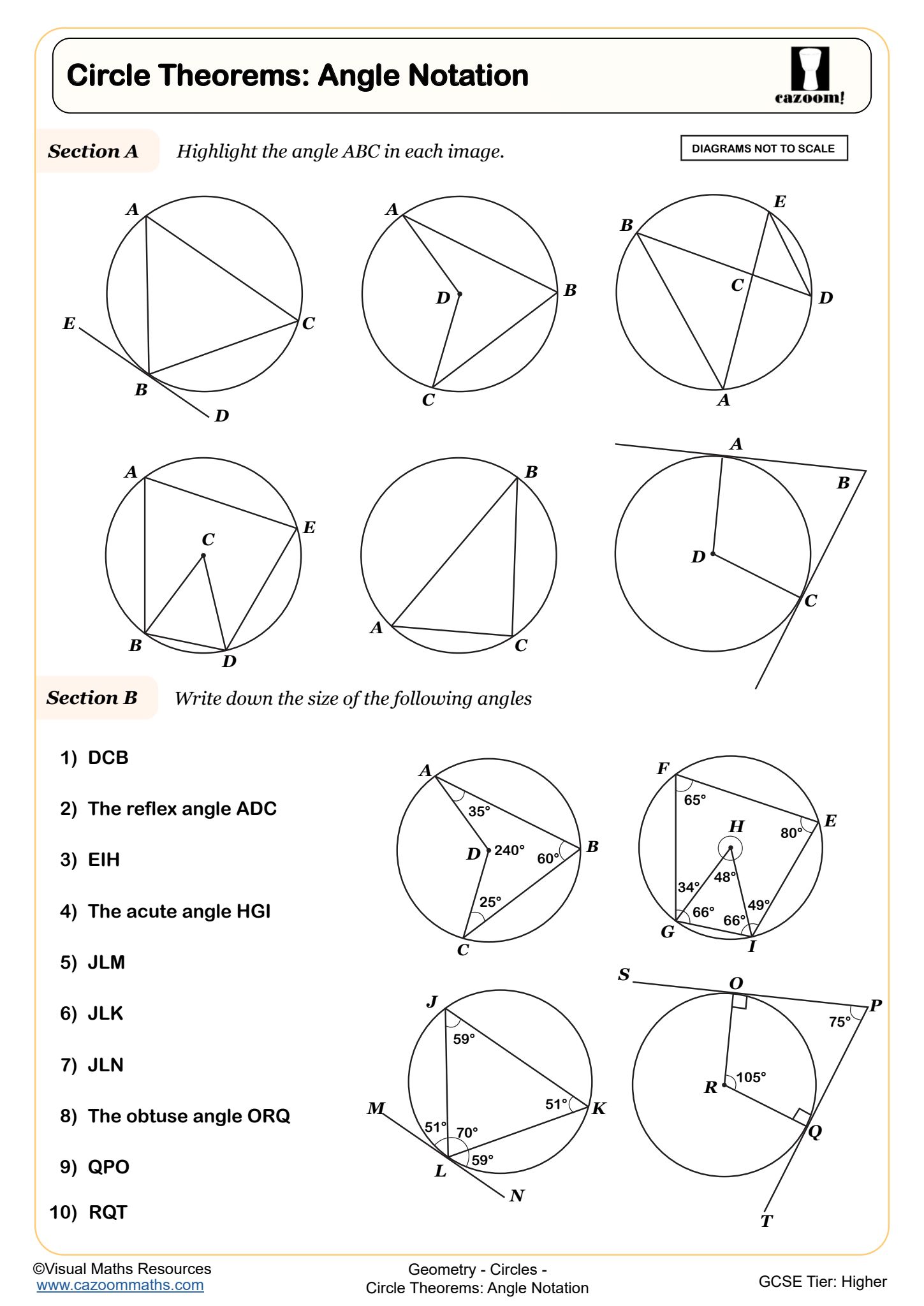
Circle Theorems: Cyclic Quadrilaterals

Circle Theorems: Triangles in Circles
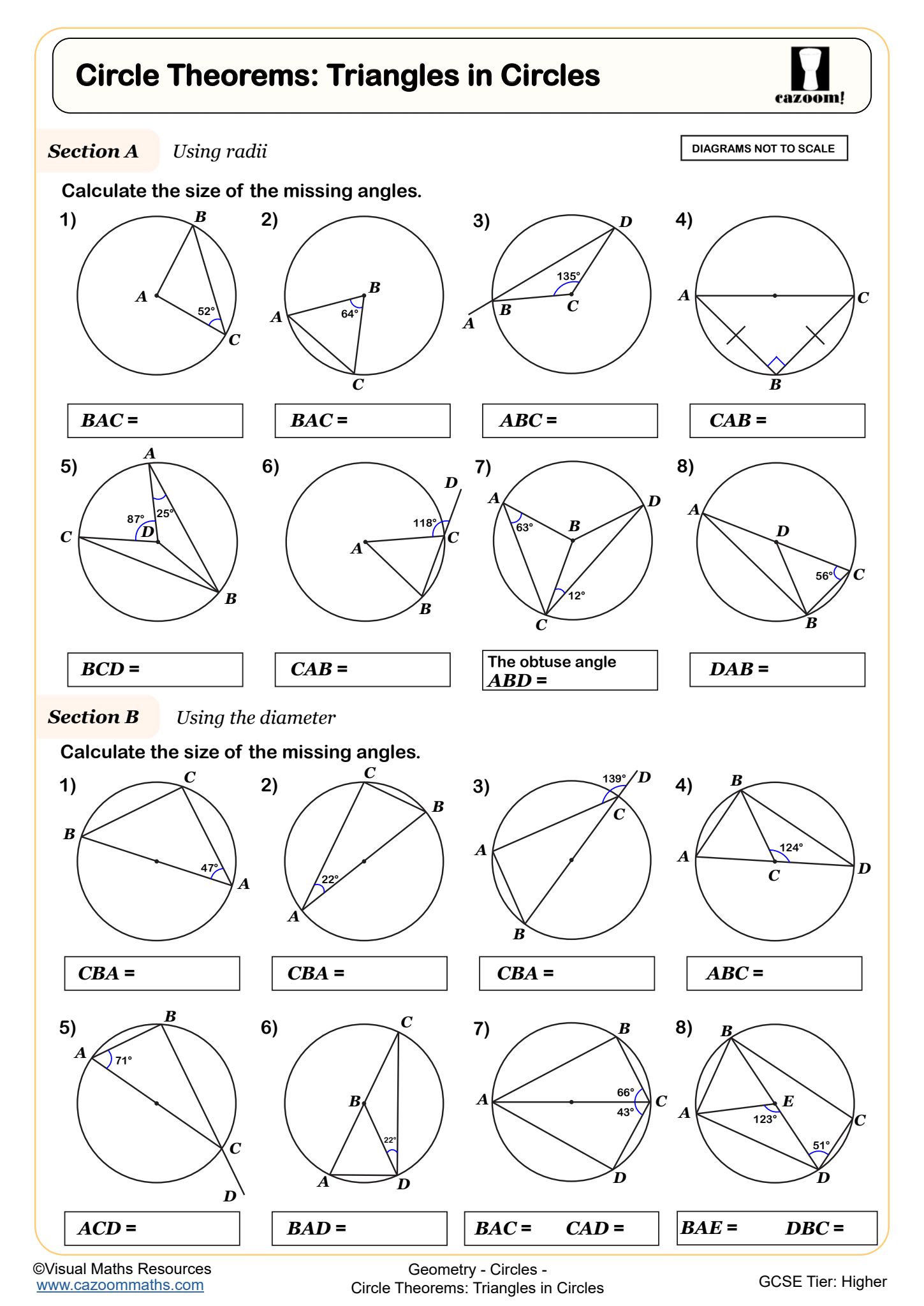
Finding the Radius or Diameter from the Circumference and Area
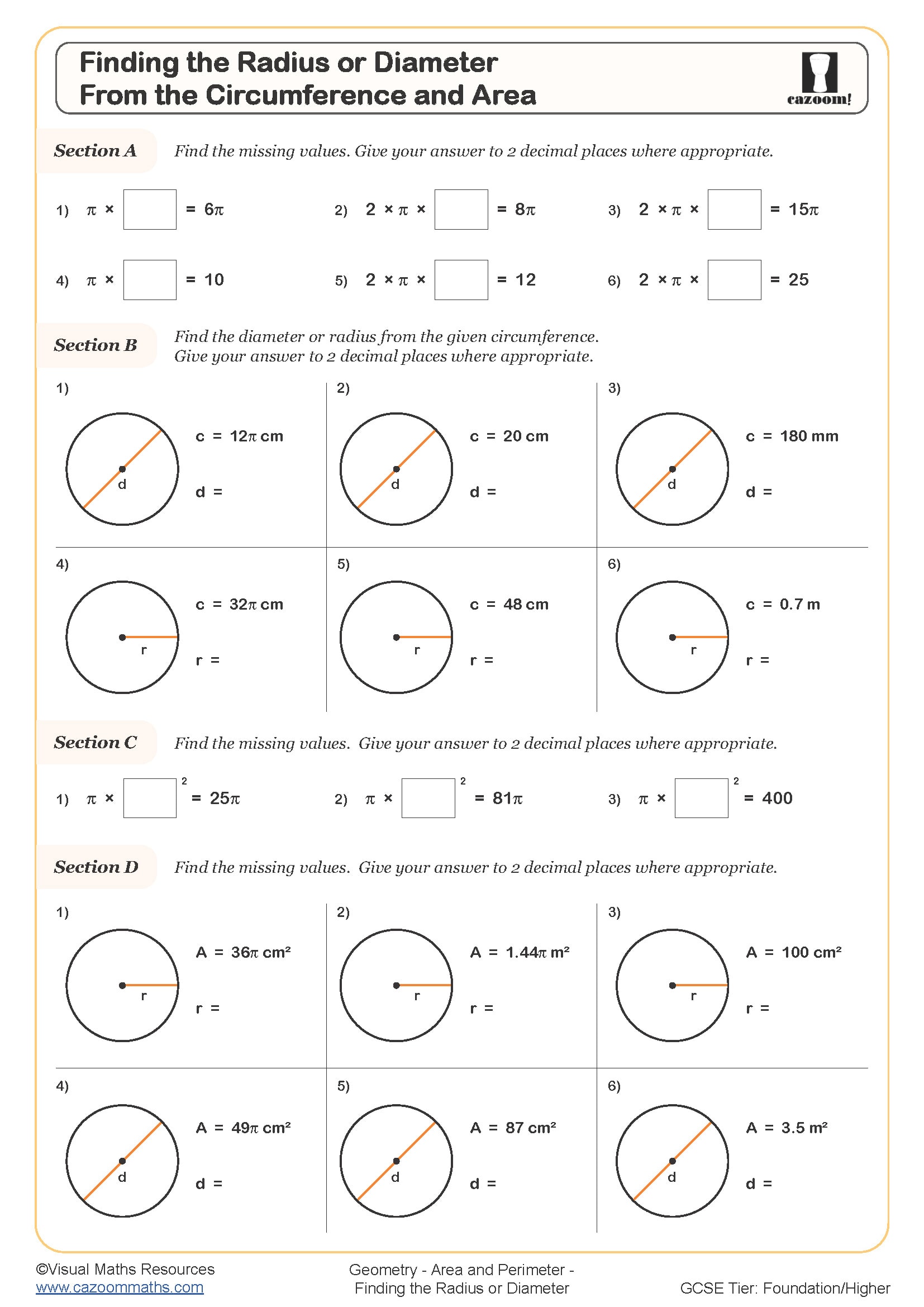
In Terms of Pi (B)

In Terms of Pi (C)
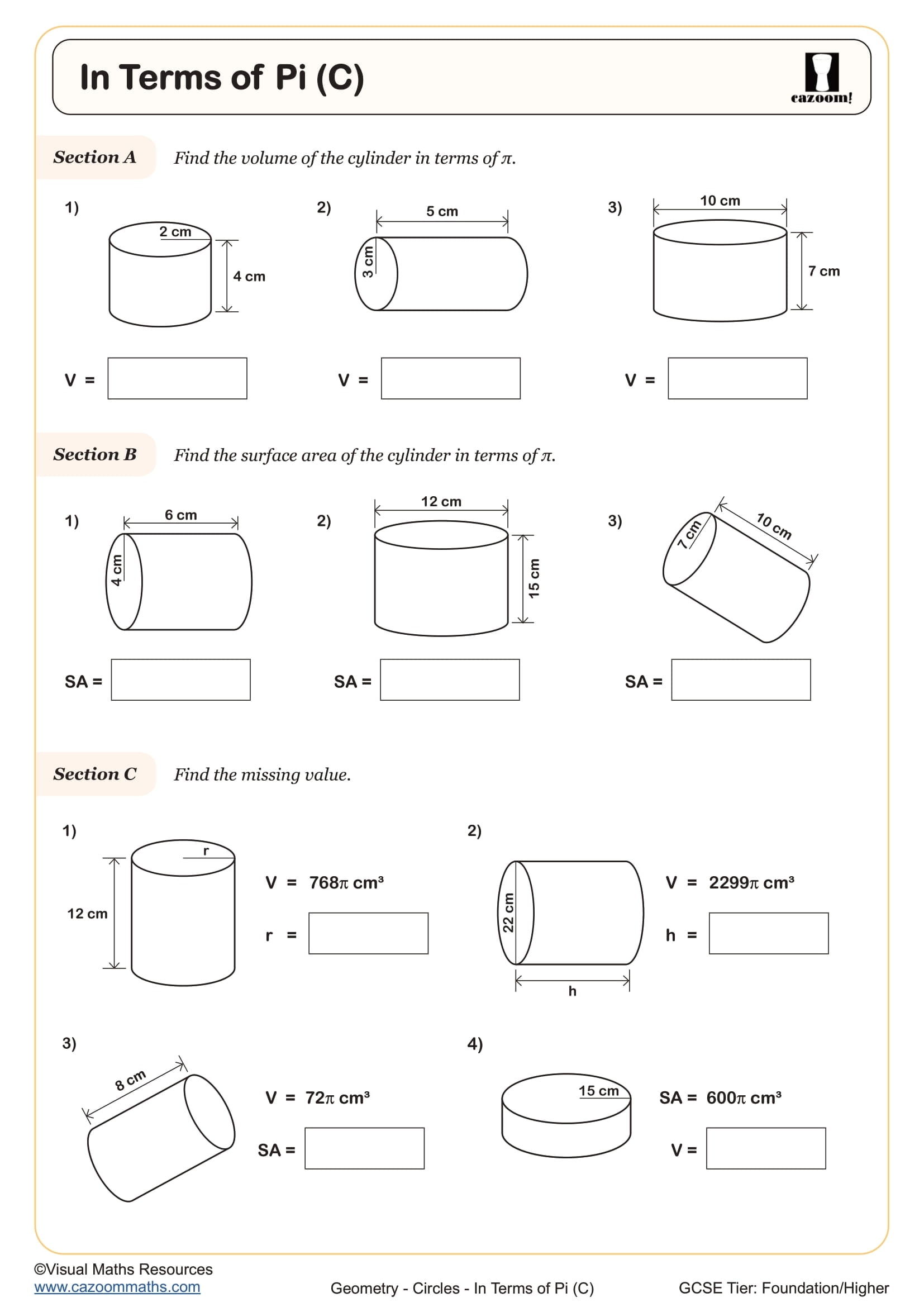
In Terms of Pi (D)
Introducing Radians

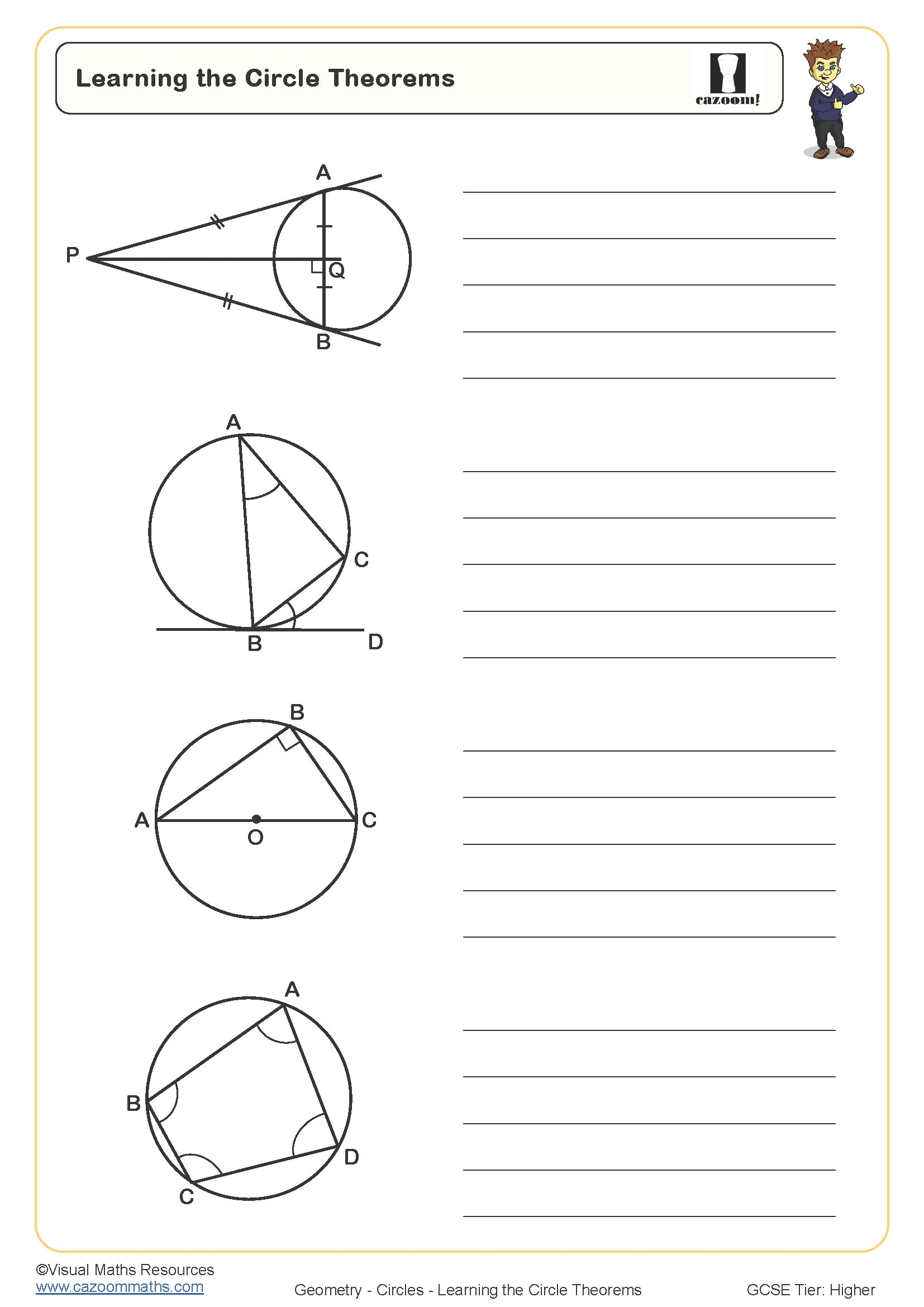
Learning the Circle Theorems
Perimeter of Sectors
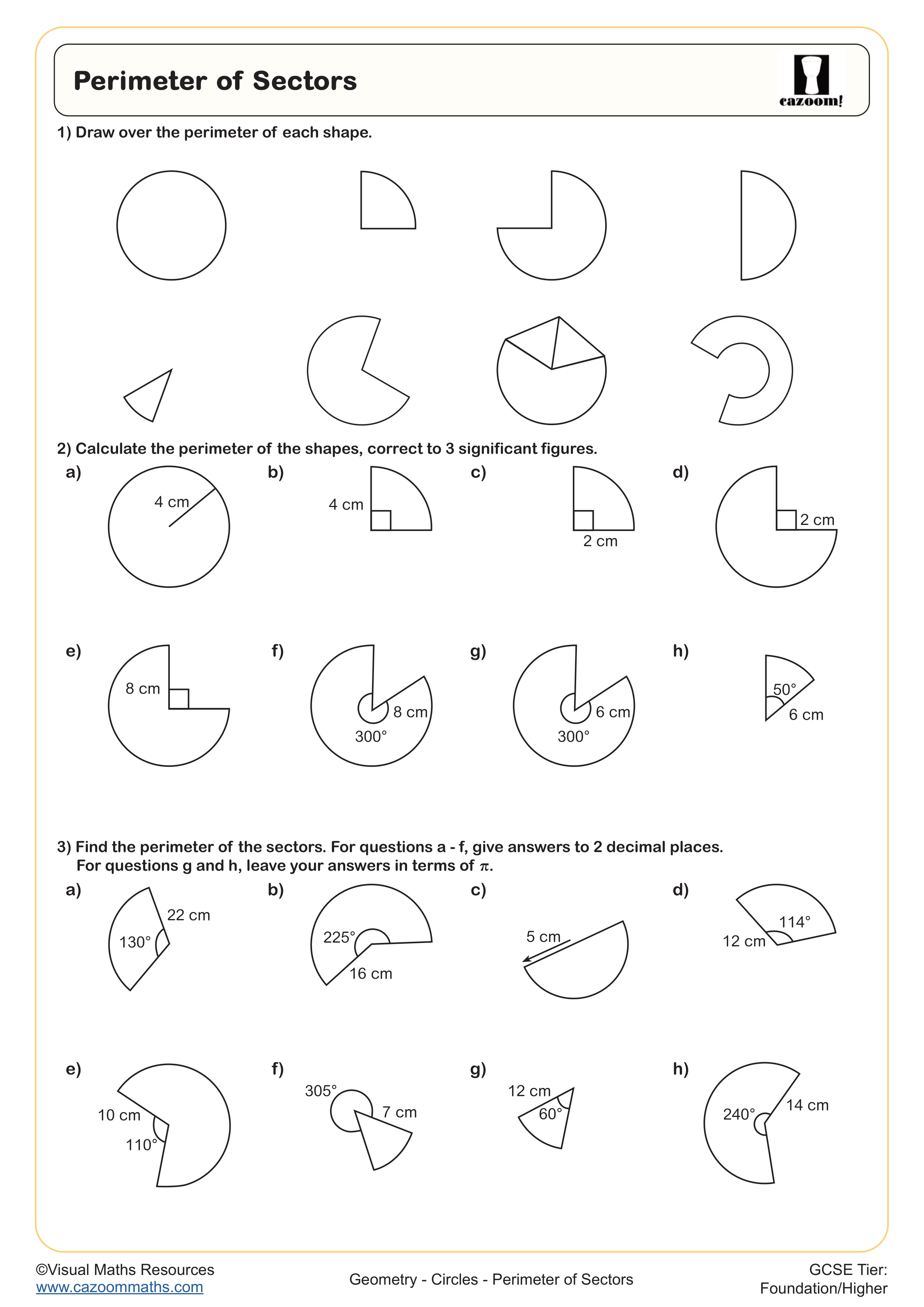
Proving Circle Theorems
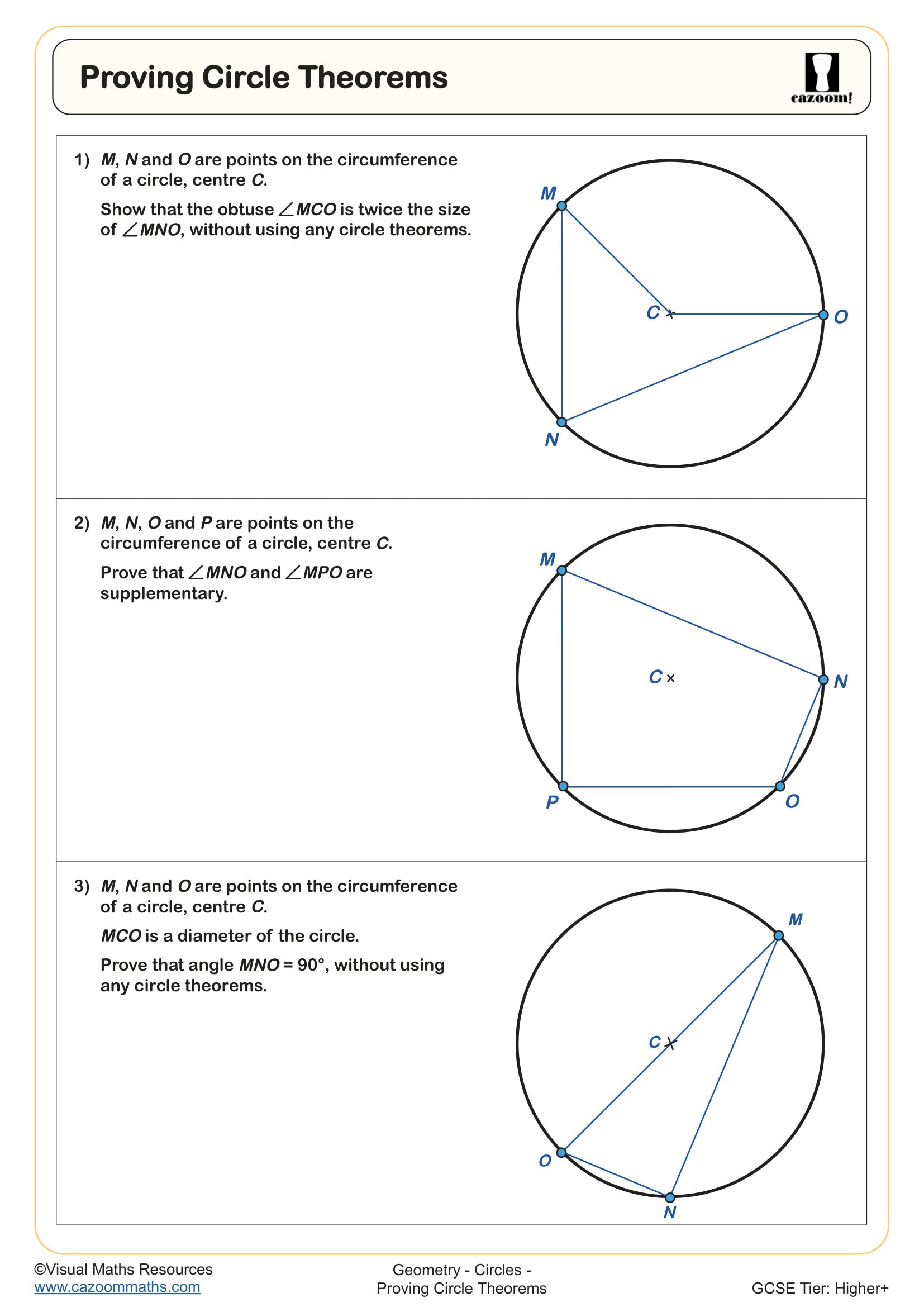
Proving Circle Theorems - Angle at the Centre
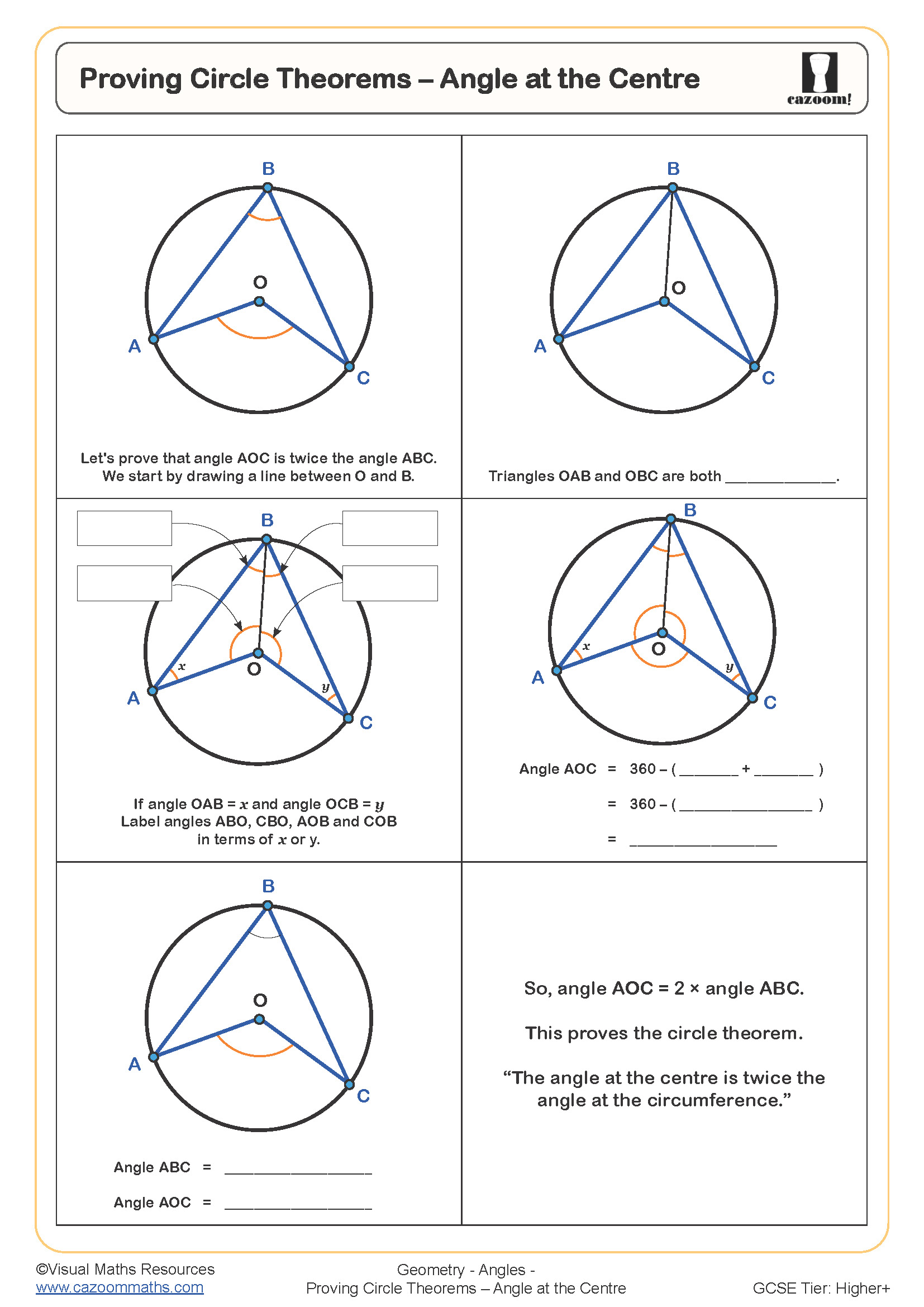
Proving Circle Theorems - Angle in a Semicircle
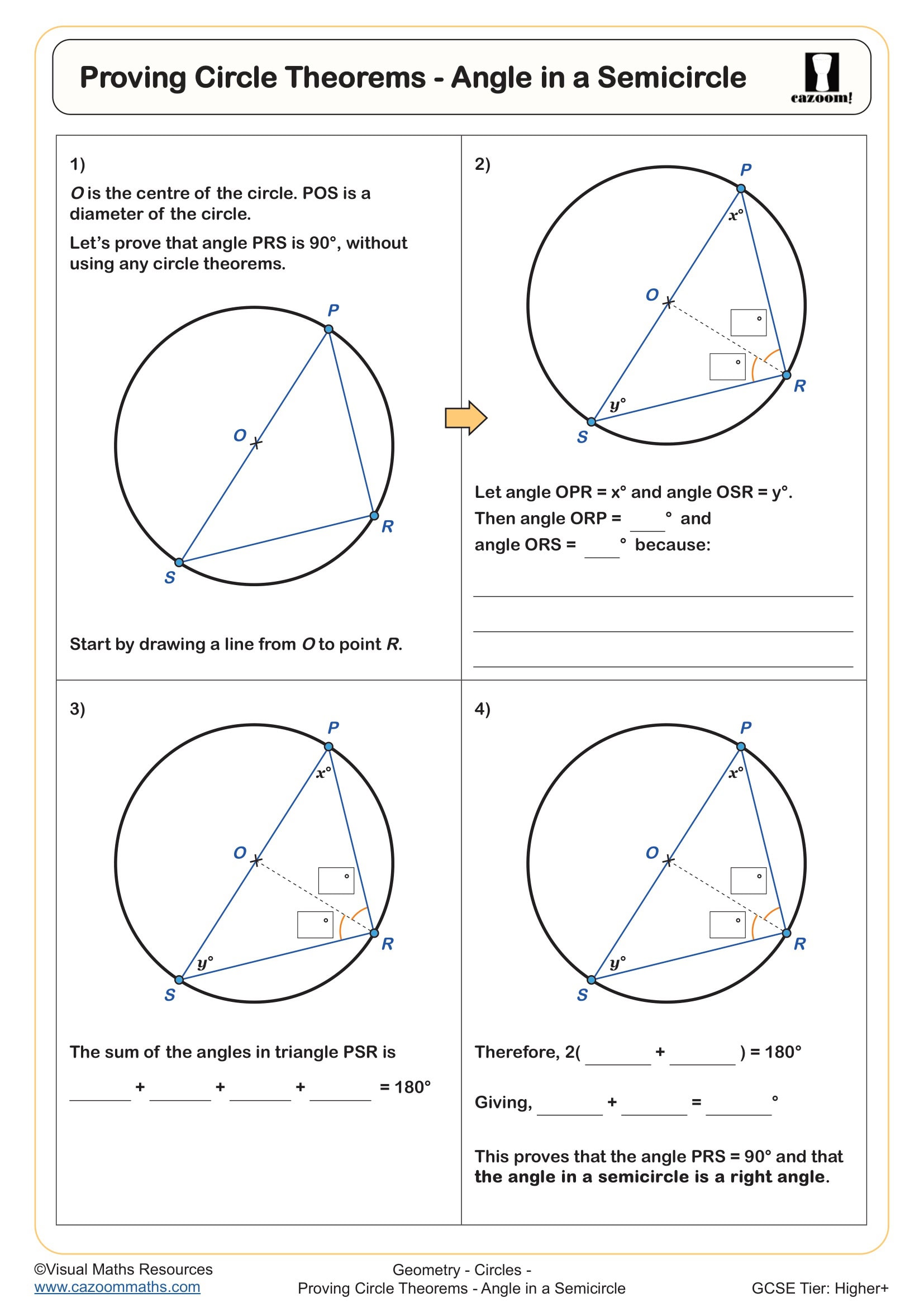
Proving Circle Theorems - Angles in the Same Segment
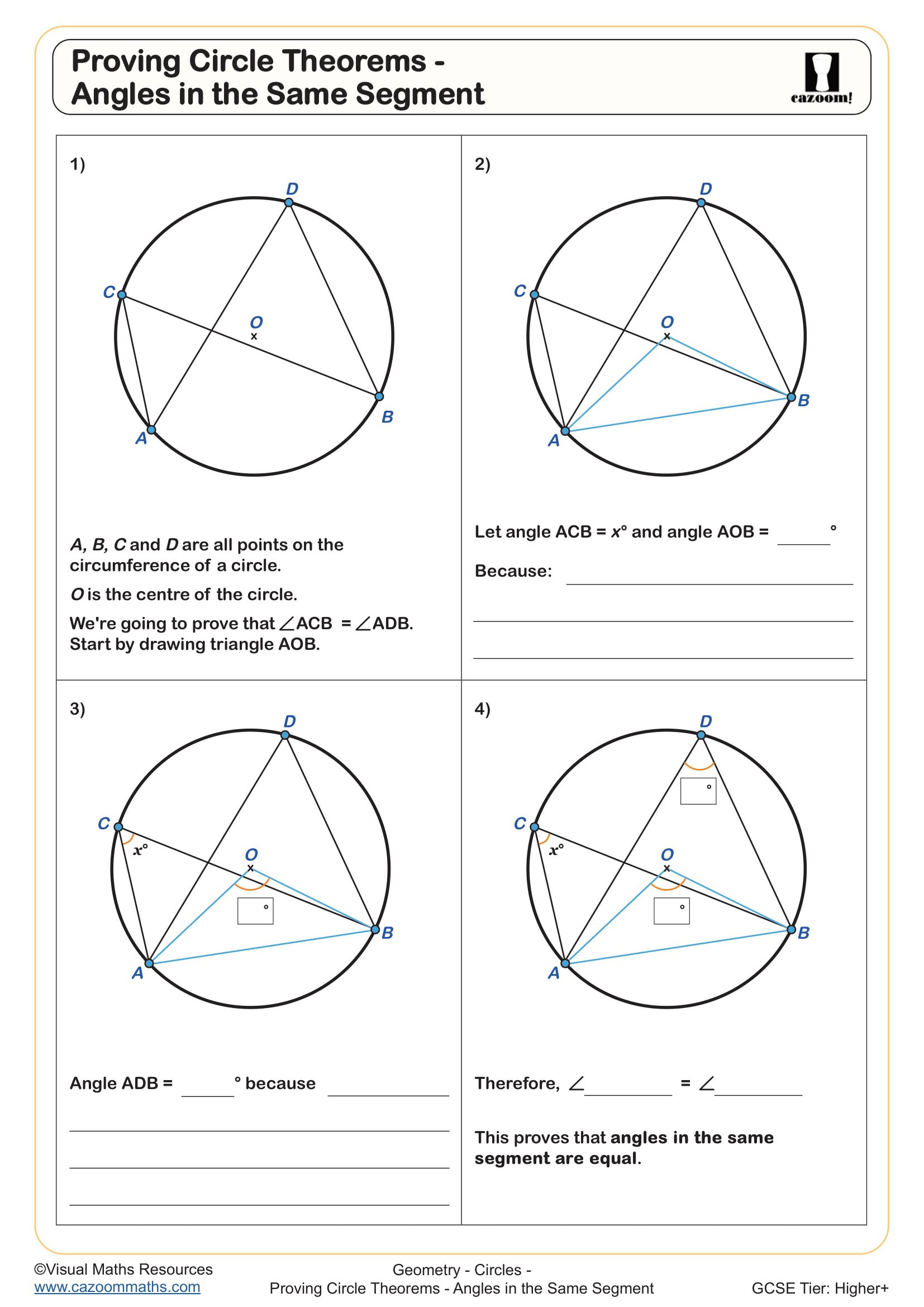
Proving Circle Theorems - Cyclic Quadrilaterals
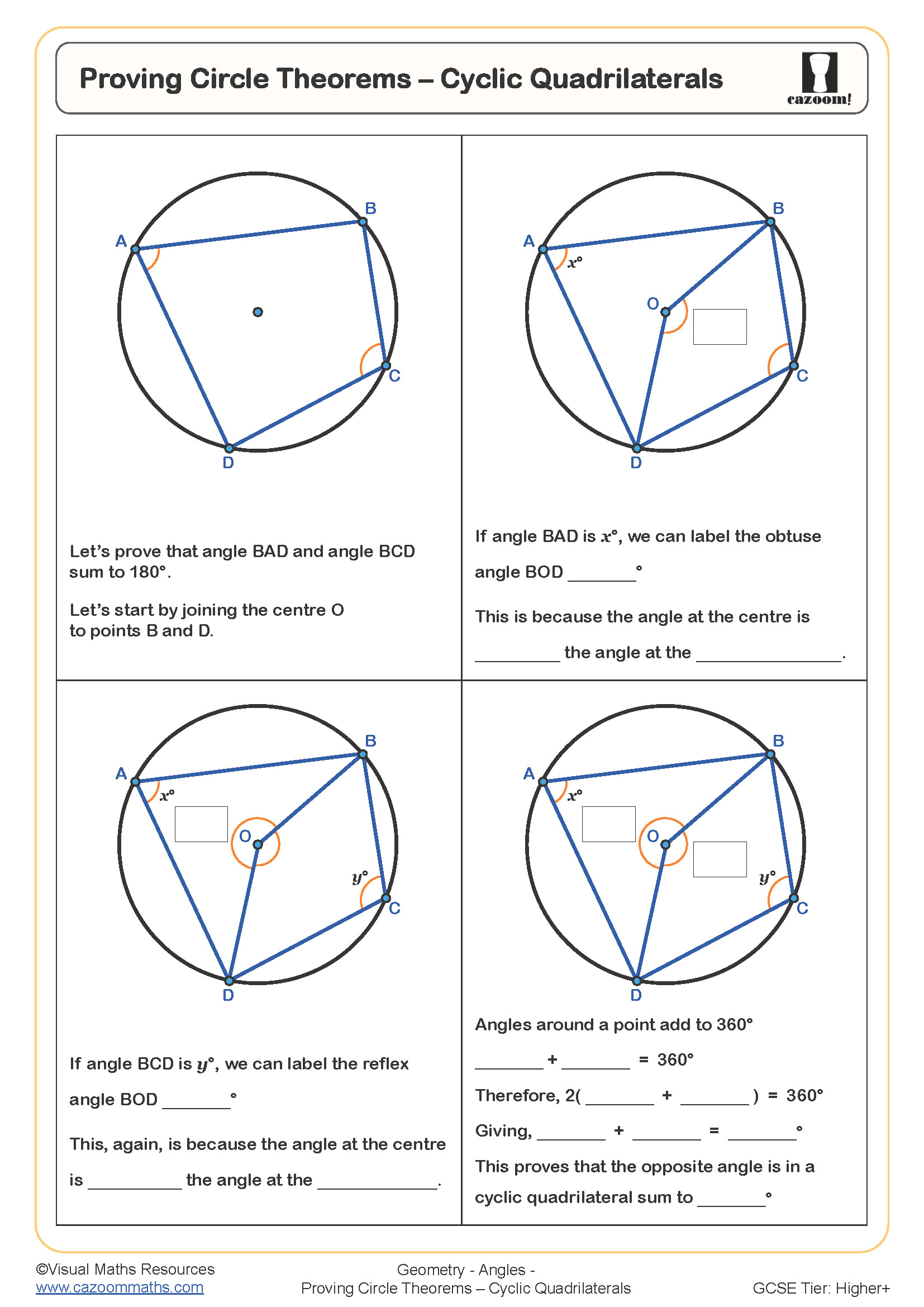
The Formulae for Area of Sectors and Arc Lengths
What are the key circle theorems students need for GCSE?
Students need to know eight main circle theorems for GCSE: the angle in a semicircle is 90°, angles in the same segment are equal, the angle at the centre is twice the angle at the circumference, opposite angles in a cyclic quadrilateral sum to 180°, the angle between a tangent and radius is 90°, tangents from an external point are equal in length, the perpendicular from the centre to a chord bisects the chord, and the alternate segment theorem. Higher tier students must also apply these in formal proofs.
Exam mark schemes penalise students who state theorems incorrectly or fail to justify their reasoning. A common error occurs when students identify the correct theorem but apply it to the wrong angle—particularly with the alternate segment theorem where they confuse which angle equals which. Students lose marks when they don't clearly label their diagrams or show which theorem they've used, even when their numerical answer is correct.
Which year groups study circles worksheets at KS4?
These circles worksheets are designed for Year 10 and Year 11 students following the GCSE Mathematics curriculum. Circle theorems typically appear in Year 10 after students have secured their understanding of angles in triangles and quadrilaterals from KS3. The topic builds on properties of shapes and reasoning skills developed in earlier key stages, introducing formal geometric proof as a new element.
The worksheets progress from Foundation tier content in Year 10, where students focus on identifying and using the basic circle theorems, to Higher tier work in Year 11 involving multi-step problems and formal proofs. Year 11 questions often combine multiple theorems in a single problem or require algebraic manipulation alongside circle properties, reflecting the increased demand of GCSE exam papers where circle theorem questions regularly appear in the higher mark questions.
What does it mean when a triangle is inscribed in a circle?
A triangle inscribed in a circle has all three vertices touching the circumference, making the circle the triangle's circumscribed circle or circumcircle. This arrangement is fundamental to several circle theorems, particularly the angle in a semicircle theorem and angles subtended by the same arc. Students must recognise that when a triangle is inscribed in a circle with one side as the diameter, the angle opposite that diameter is always 90°, creating a right-angled triangle.
This principle has practical applications in engineering and architecture. Surveyors use the property that any angle inscribed in a semicircle is a right angle to establish perpendicular lines when planning building layouts. Navigation systems exploit inscribed angle theorems when calculating positions using multiple reference points—the same mathematics underpins GPS triangulation methods and satellite positioning systems that determine location based on angles and distances from known points.
How do these circle worksheets help students prepare for GCSE exams?
The worksheets provide structured practice that mirrors GCSE question styles, starting with straightforward theorem identification and building towards the multi-step reasoning problems that appear in Paper 2 and Paper 3. Questions require students to find missing angles using combined theorems, write formal geometric arguments, and apply algebraic skills alongside circle properties. The answer sheets show clear working and theorem justifications, helping students understand the level of detail examiners expect.
Teachers use these resources flexibly across different settings: as retrieval practice at the start of lessons to maintain previously learned theorems, for targeted intervention with students who struggle to select the correct theorem, and as homework to reinforce classroom teaching. The worksheets work well for paired activities where students explain their reasoning to each other, addressing the common weakness of knowing theorems but failing to articulate geometric arguments clearly in exam conditions.