KS4 Pythagoras Worksheets
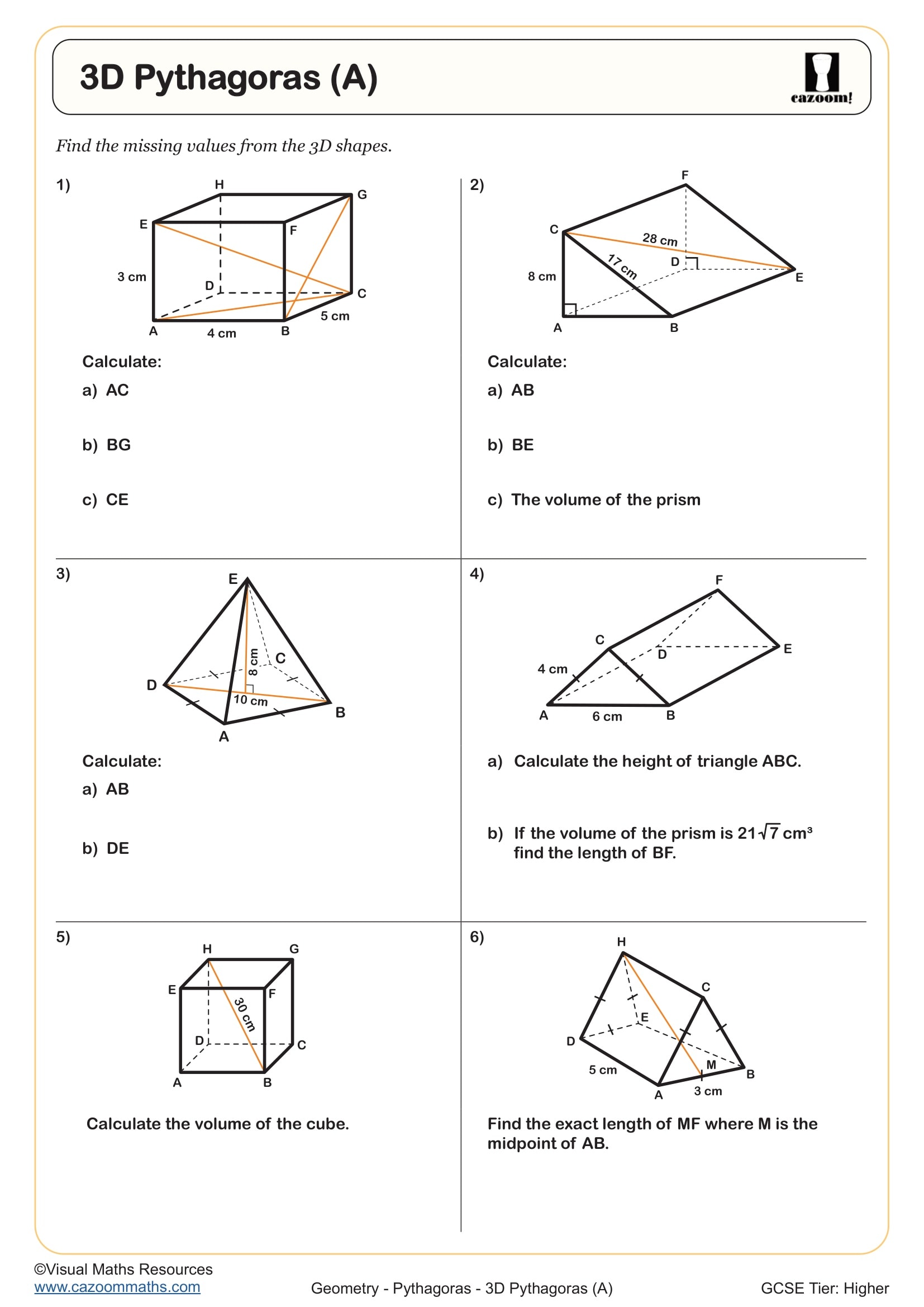
3D Pythagoras (A)
3D Pythagoras (B)

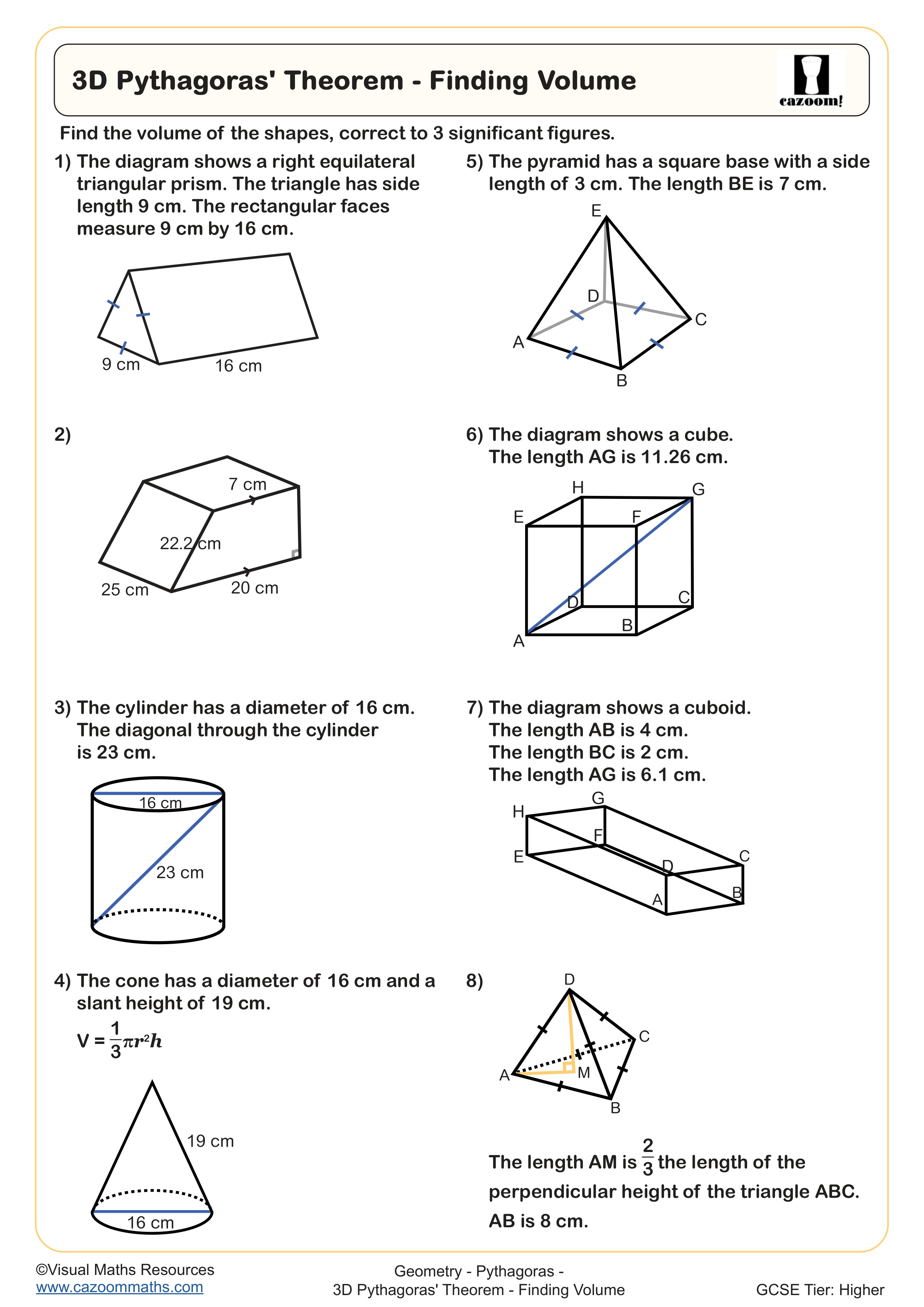
3D Pythagoras' Theorem - Finding Volume
Area of a Triangle Using Pythagoras' Theorem

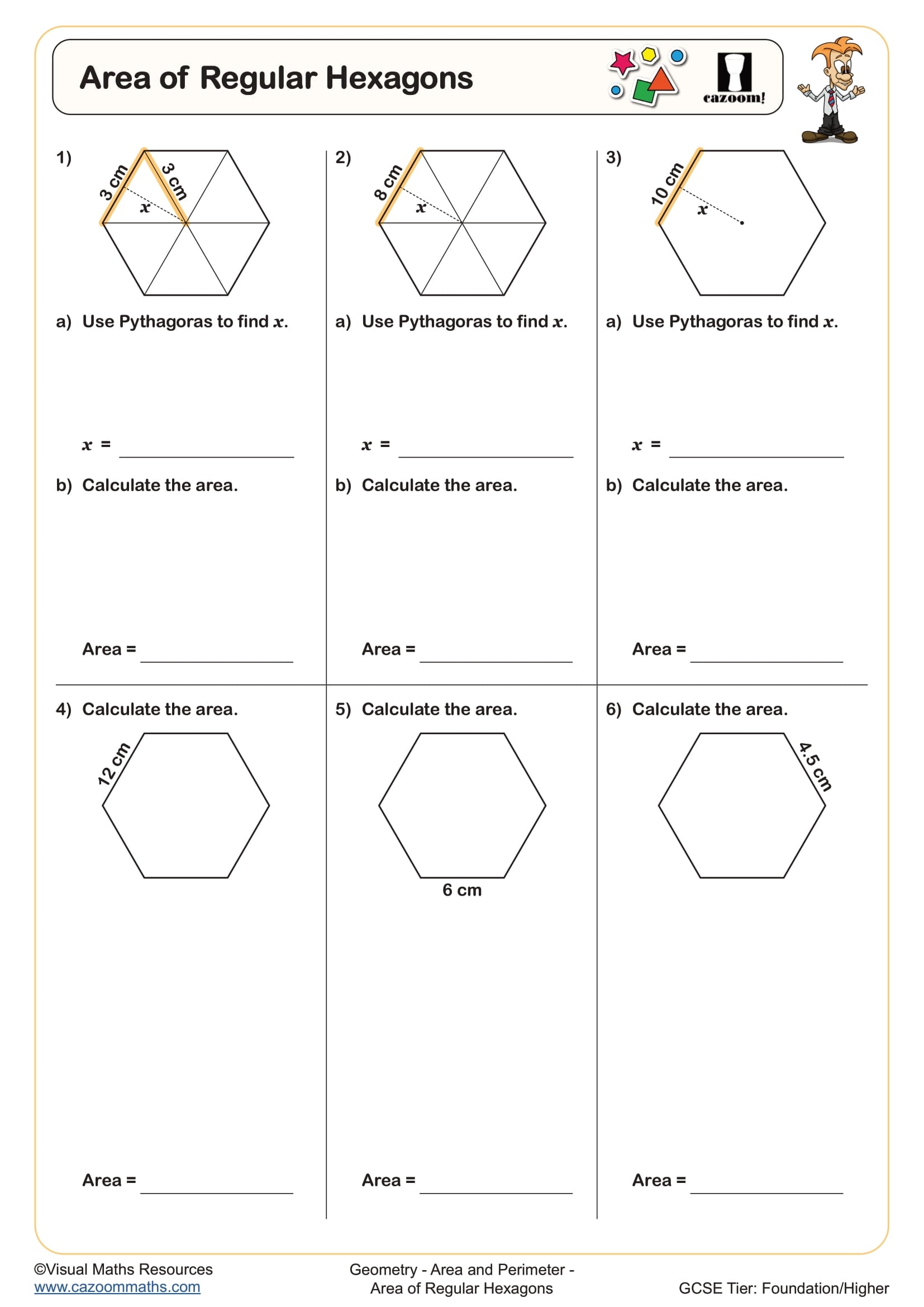
Area of Regular Hexagons
Identifying Right Angled Triangles

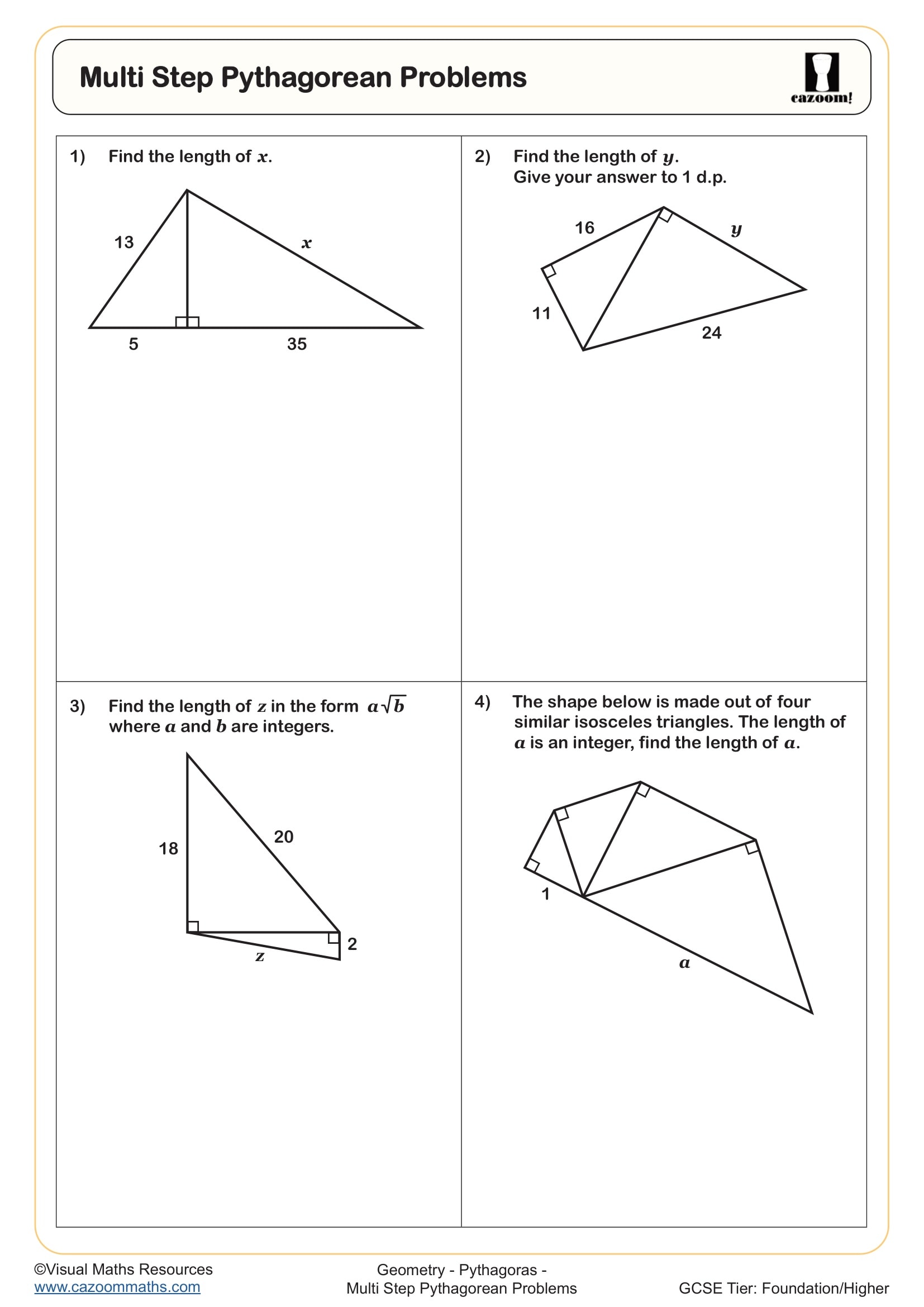
Multi Step Pythagorean Problems
Perimeter Using Pythagoras' Theorem

Pythagoras and Coordinates
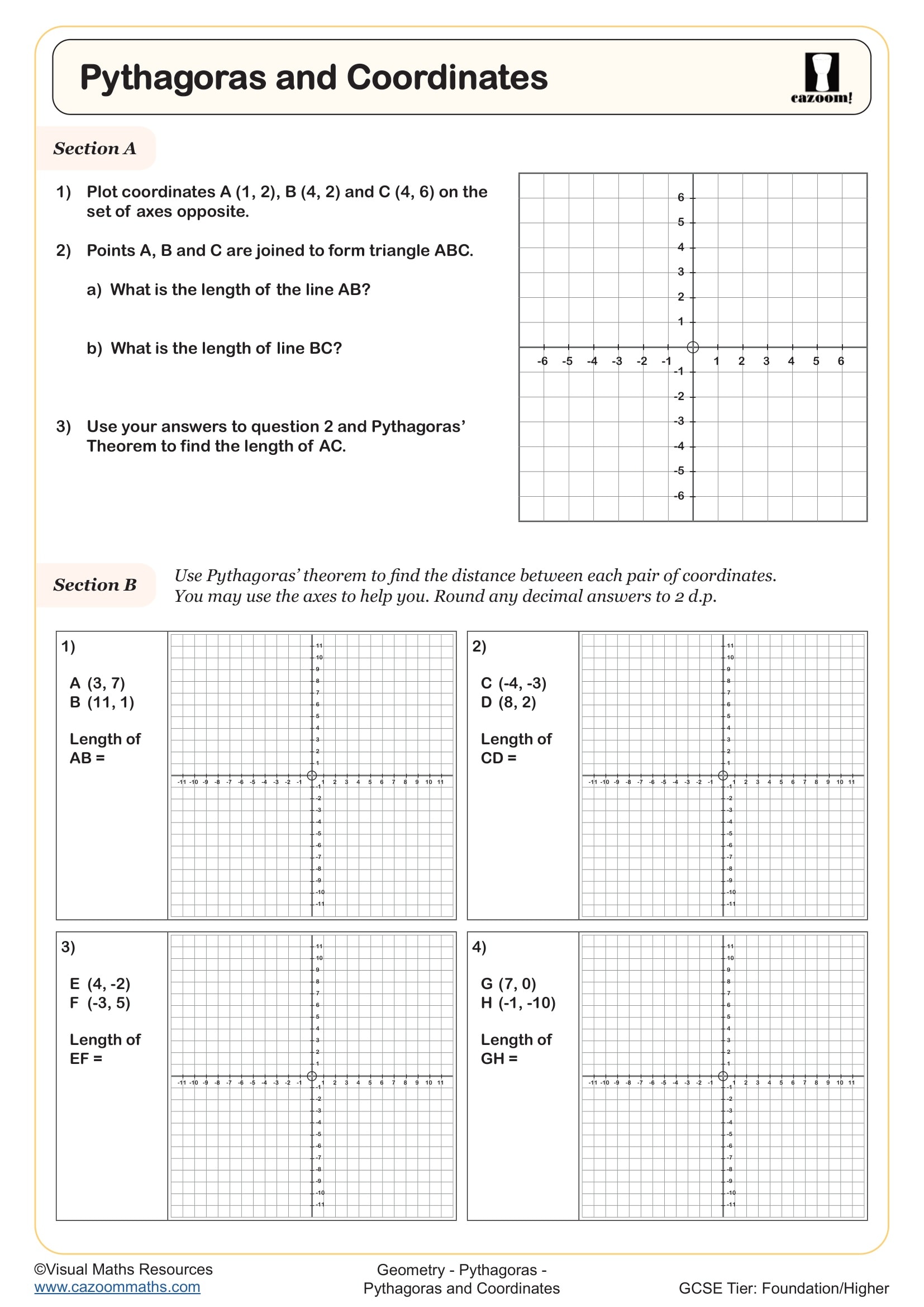
Pythagoras or Trigonometry? (A)
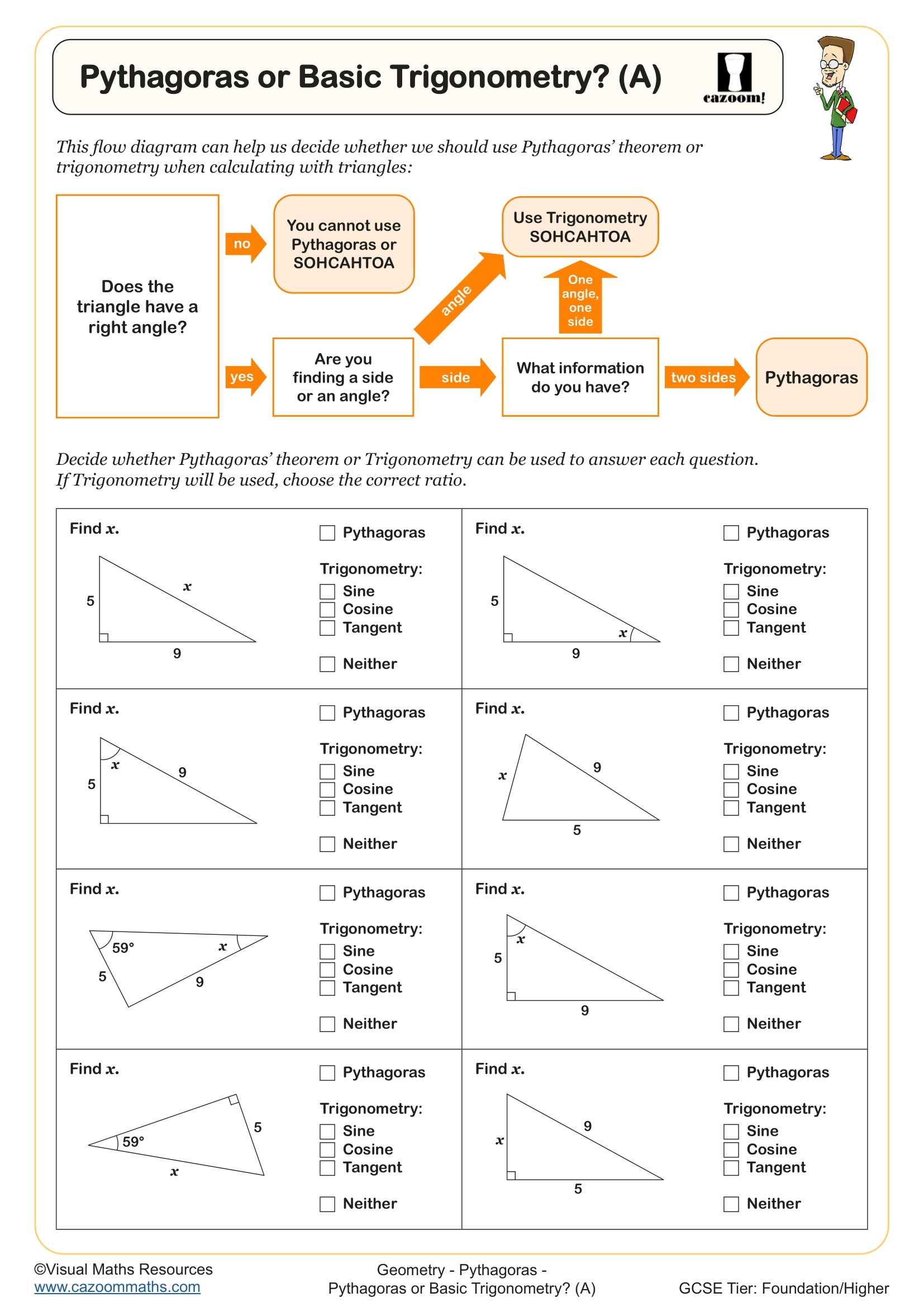
Pythagoras or Trigonometry? (B)
Pythagoras with Surds

Pythagoras Word Problems

Pythagoras Word Problems (With Clues)

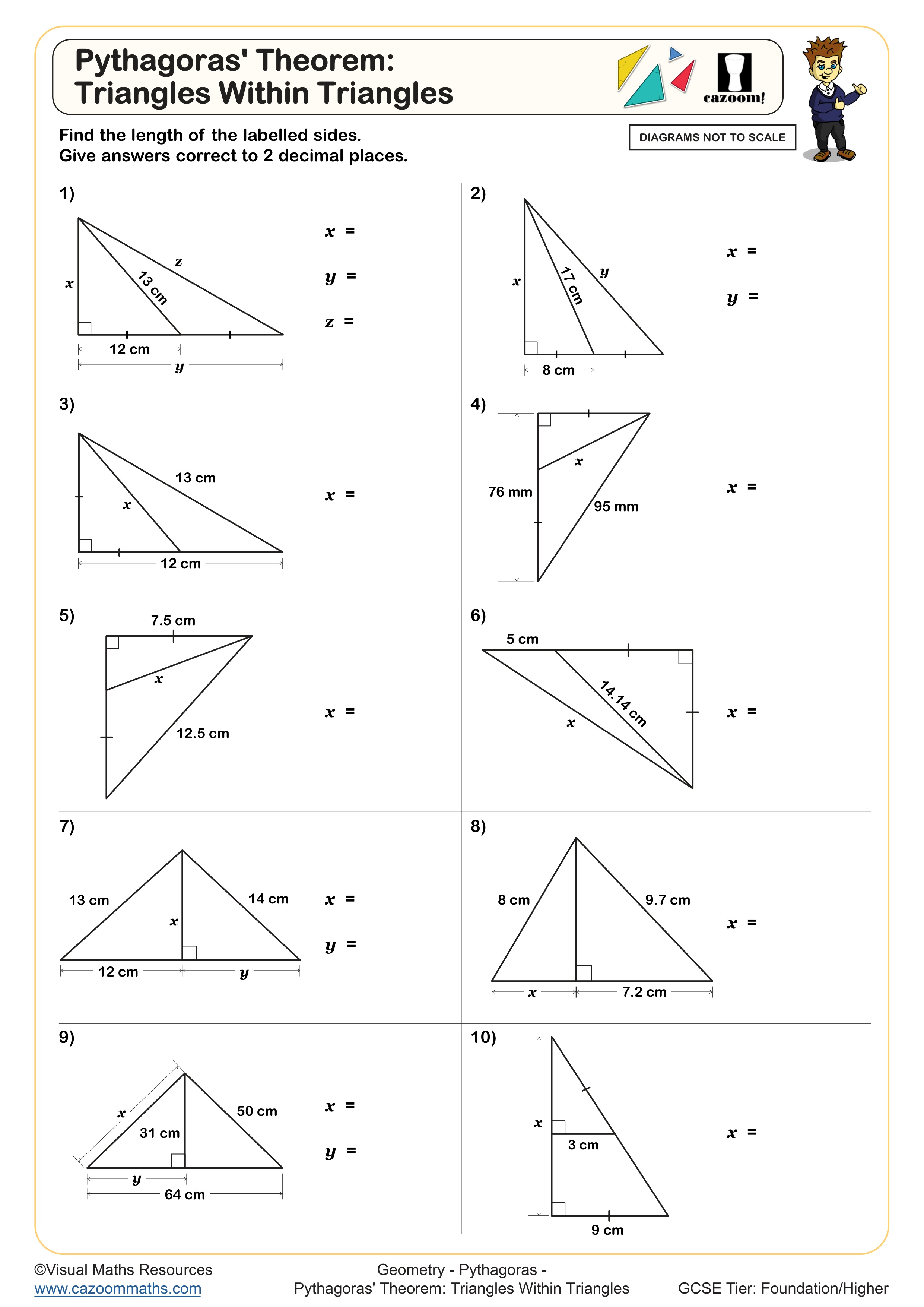
Pythagoras' Theorem: Triangles Within Triangles
Using Pythagoras Theorem to Calculate the Hypotenuse
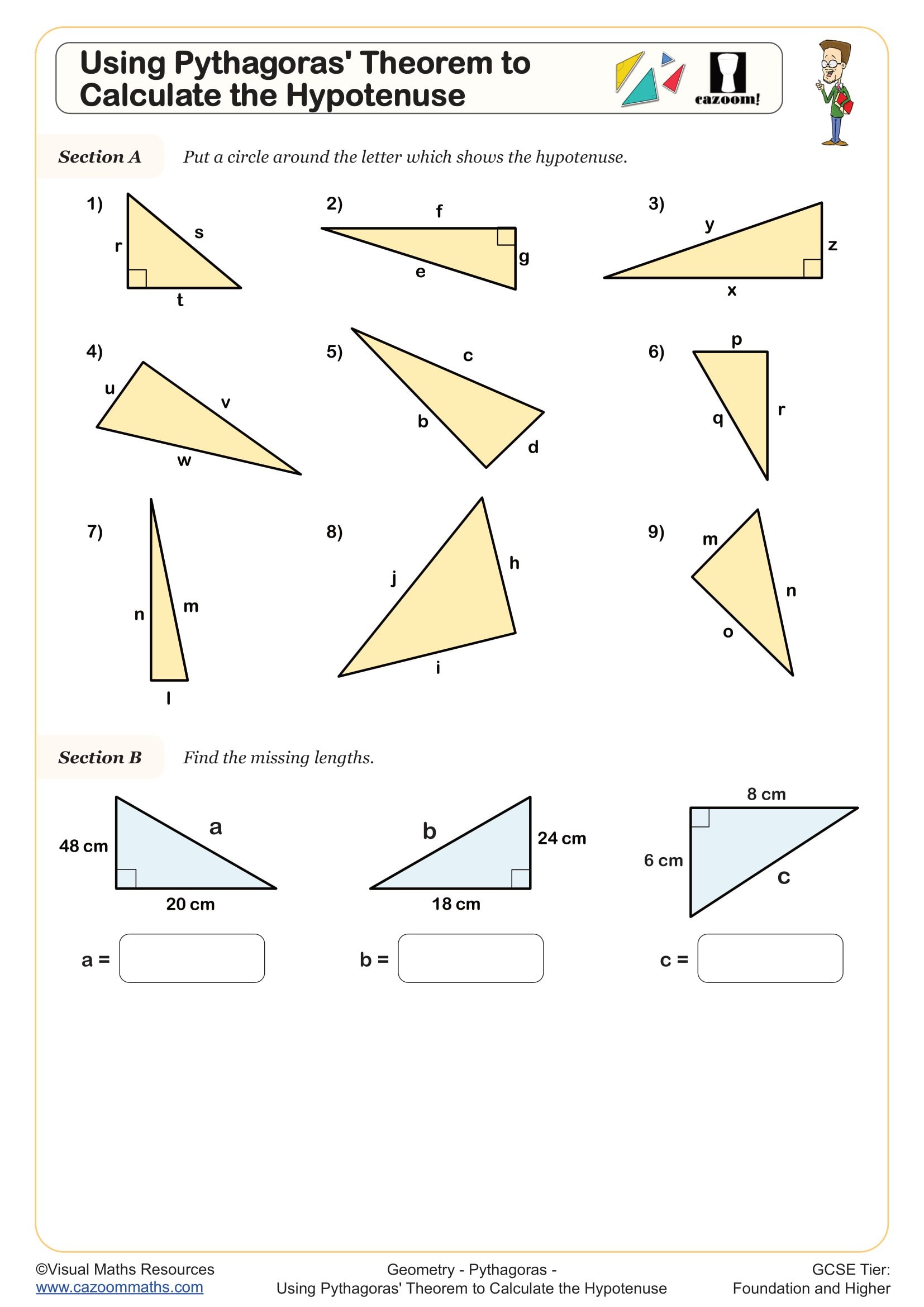
Using Pythagoras' Theorem to Calculate Missing Lengths in Right Angled Triangles

What types of problems are included in these Pythagoras worksheets?
The worksheets cover the full GCSE specification for Pythagoras' theorem, starting with identifying hypotenuse versus shorter sides, then progressing to finding missing lengths in right-angled triangles. More challenging problems include calculating coordinates where students use Pythagoras to find distances between points, triangles within shapes where students must first identify the relevant right-angled triangle, and volume problems requiring Pythagorean calculations as an intermediate step.
Students often lose marks on clue-based problems where they must interpret a diagram to spot the right-angled triangle, particularly when it's embedded within a composite shape. Questions involving surds are common at higher GCSE, and mark schemes specifically require exact answers left in surd form rather than rounded decimals, something students frequently forget under exam pressure.
Which year groups study Pythagoras' theorem?
Pythagoras' theorem is introduced at KS4, typically in Year 10, as part of the geometry and measures strand of the National Curriculum. Year 11 students revisit the theorem during GCSE revision and encounter it embedded within more complex problems across various topics including trigonometry, vectors, and 3D shapes. Both foundation and higher tier students are expected to apply the theorem confidently.
The difficulty progression from Year 10 to Year 11 moves from isolated triangle problems with clearly labelled diagrams toward multi-step applications. By Year 11, students tackle problems where identifying that Pythagoras is needed becomes the first challenge, such as finding the perpendicular height of an isosceles triangle or calculating space diagonals in cuboids. Higher tier students must also work fluently with exact answers involving surds rather than calculator approximations.
How does Pythagoras connect to finding coordinates?
Using Pythagoras to find distances between coordinates combines algebraic and geometric thinking. Students calculate the horizontal and vertical distances between two points, then treat these as the two shorter sides of a right-angled triangle, with the straight-line distance as the hypotenuse. This approach underpins the formal distance formula taught at A-level, though at GCSE students typically work through the Pythagorean calculation step by step.
This skill has direct applications in navigation systems and GPS technology, where calculating the straight-line distance between two positions is fundamental. In engineering and architecture, coordinate-based distance calculations help determine material lengths, cable runs, and structural measurements. Students working towards STEM subjects will encounter this constantly, from physics displacement problems to computer graphics programming where screen coordinates determine distances between objects.
How can teachers use these worksheets effectively?
The worksheets build systematically from identifying right-angled triangles and labelling sides correctly through to complex applications, allowing teachers to select sheets that match current teaching objectives. Starting with simpler problems where the triangle is clearly marked helps establish the formula before introducing questions where students must first spot which triangle to use. The answer sheets enable students to self-check during independent practice, encouraging them to identify and correct errors immediately rather than embedding misconceptions.
Many teachers use these worksheets for targeted intervention with students who struggle to transfer Pythagoras into problem-solving contexts, particularly those who can apply the formula in isolation but fail to recognise when it's needed. They work well as homework following initial teaching, as starters to maintain fluency during the run-up to exams, or for paired work where students explain their reasoning to each other. The variety of question types means teachers can differentiate easily within mixed-attainment groups.