KS4 Rearranging Equations Worksheets
What are the key steps for rearranging equations?
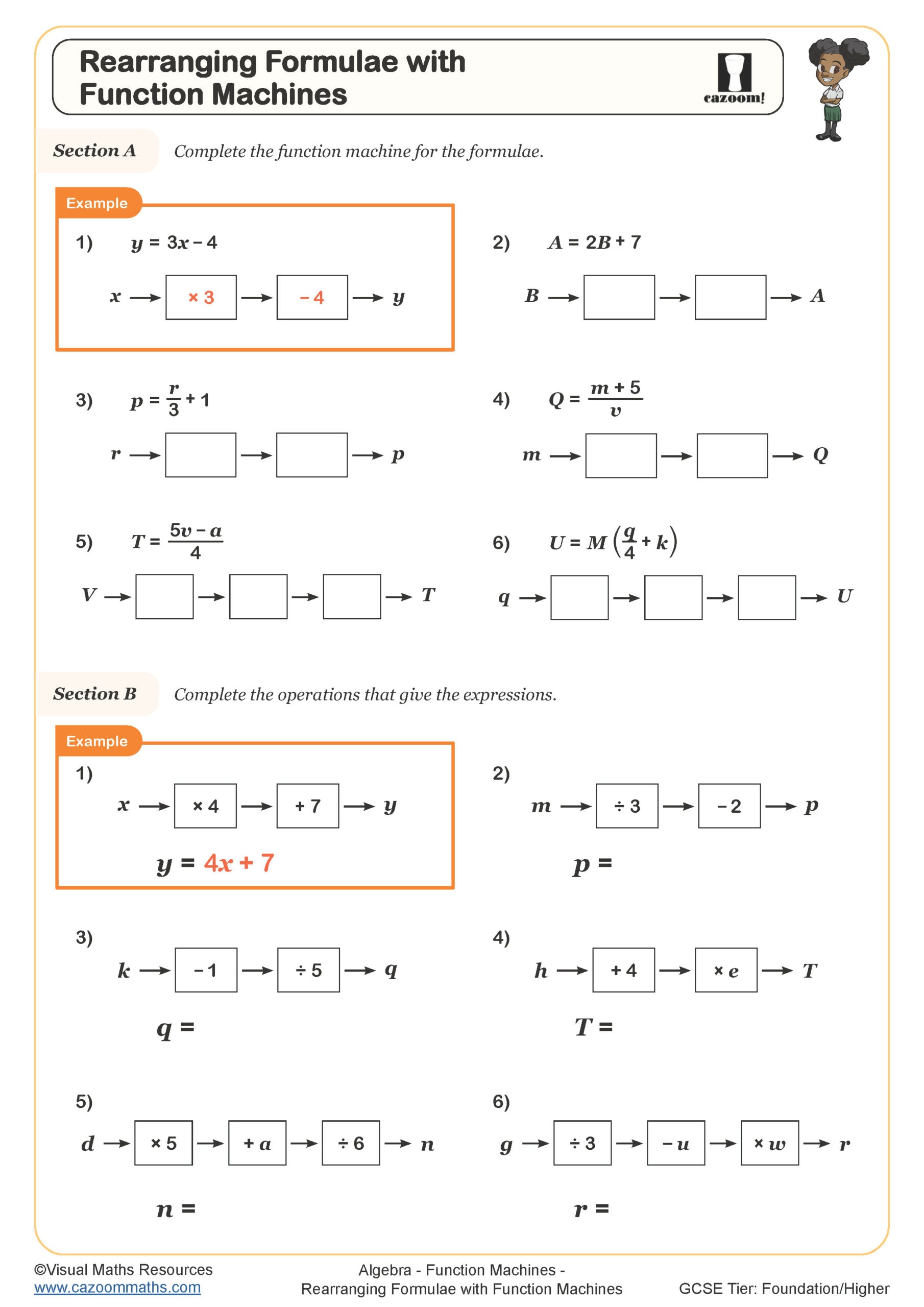
Rearranging equations requires a methodical approach using inverse operations in reverse order of BIDMAS. Students identify the variable to be made the subject, then systematically undo operations affecting it, working from the outside in. Each step must be applied to both sides of the equation to maintain equality, a principle central to algebraic manipulation at GCSE level.
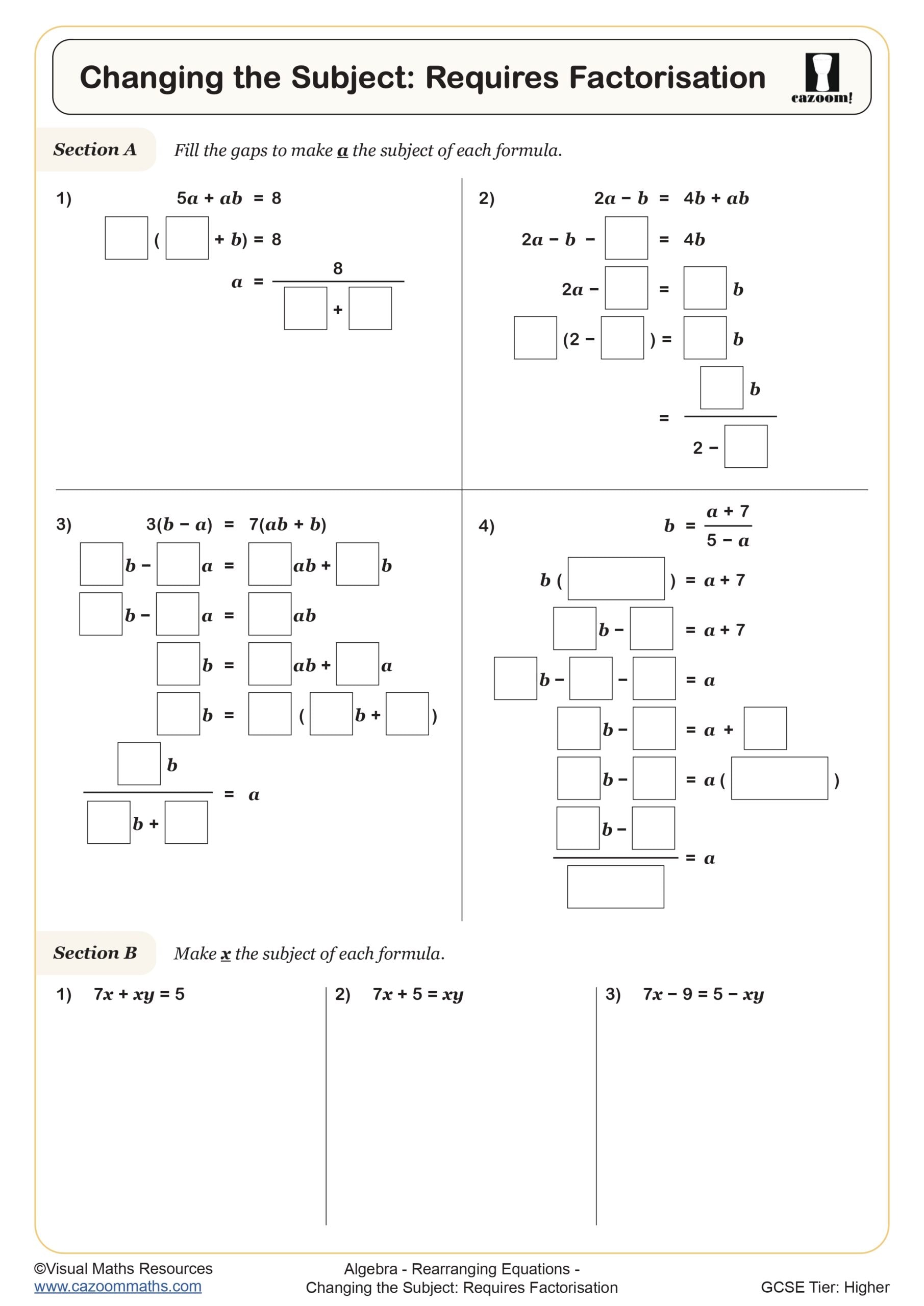
A common error occurs when students attempt to isolate a variable that appears in multiple terms without first collecting like terms. For example, when rearranging p = 3q + r - q to make q the subject, students frequently forget to combine 3q and -q into 2q before dividing. Mark schemes consistently penalise failing to show each step clearly, particularly when dealing with negative coefficients or fractional multipliers.
Which year groups study rearranging equations?
Rearranging equations is a KS4 topic taught across Year 10 and Year 11 as part of the algebra strand in the National Curriculum. Students first encounter making a variable the subject with simple linear formulae before progressing to more demanding rearrangements involving multiple variables. This skill is assessed at both Foundation and Higher tier GCSE, though the complexity differs significantly between levels.
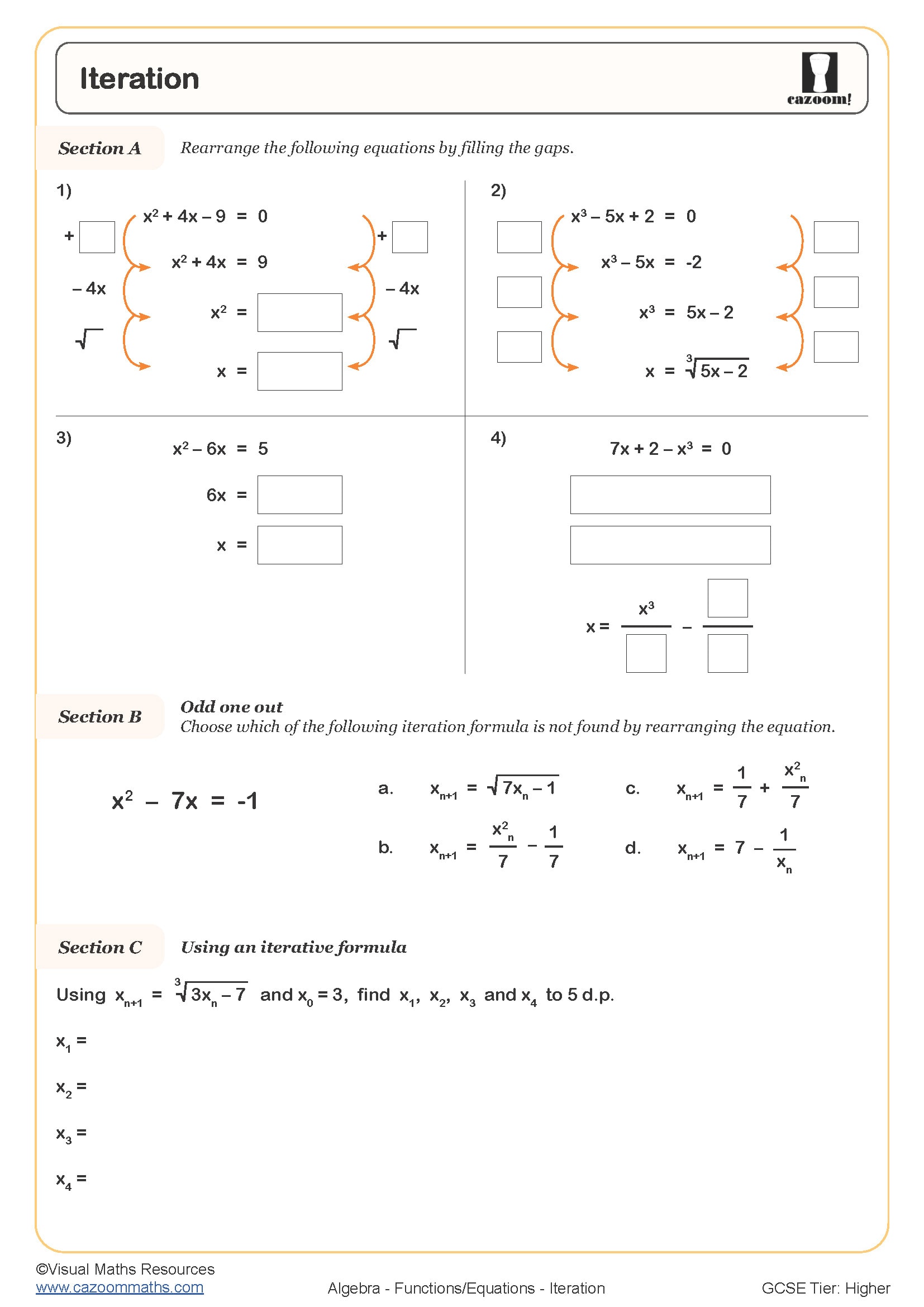
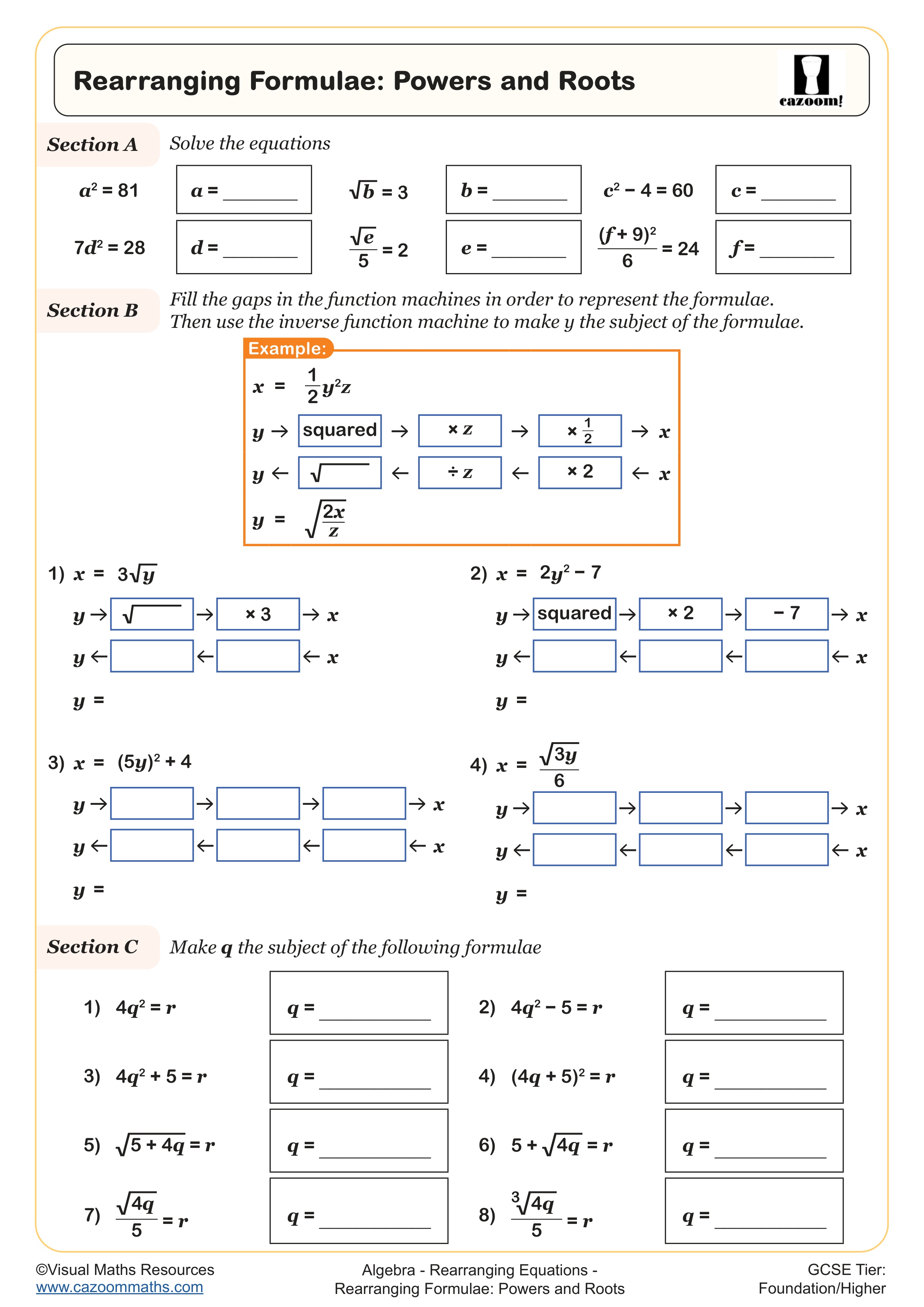
Progression typically moves from one-step rearrangements like making t the subject of v = t/5 to multi-step problems requiring factorisation, such as rearranging a = b + cd to make d the subject. Higher tier students tackle equations where the subject appears twice (requiring factorisation) and formulae involving squares or square roots, such as those found in physics contexts like kinetic energy or density calculations.
How do you rearrange equations with fractions?
Rearranging equations containing fractions requires multiplying both sides by the denominator as the first step to eliminate the fraction. For example, when making h the subject of v = u + h/t, students multiply both sides by t to give vt = ut + h, then subtract ut to isolate h. This approach prevents the common mistake of trying to manipulate the fraction whilst it remains in the equation, which typically leads to sign errors or incorrect inverse operations.
This technique has direct applications in science formulae that students encounter in their STEM subjects. Rearranging the density equation ρ = m/V to find mass or volume, or manipulating Ohm's law V = IR to calculate resistance, both require confident handling of fractional equations. Engineers and scientists routinely rearrange formulae to solve for unknown quantities, making this an authentic workplace skill beyond the mathematics classroom.
How can these worksheets support GCSE preparation?
The worksheets build fluency through carefully structured practice that mirrors GCSE question styles. Each sheet presents problems in increasing difficulty, allowing students to consolidate basic rearrangement skills before attempting examination-standard questions. The inclusion of complete answer sheets enables students to self-assess and identify specific error patterns, such as sign errors when subtracting terms from both sides or mistakes when dealing with coefficients.
Teachers frequently use these resources for intervention sessions with students who lose marks on method questions in mock examinations. The worksheets work effectively as homework to reinforce classroom teaching, as starter activities to recap prior learning, or during paired work where students compare solution methods. Many teachers set specific sheets as timed practice to help students develop the speed needed for GCSE papers, where rearrangement questions often appear as part of multi-step problem-solving tasks worth several marks.