Year 11 Pythagoras Worksheets
3D Pythagoras (A)
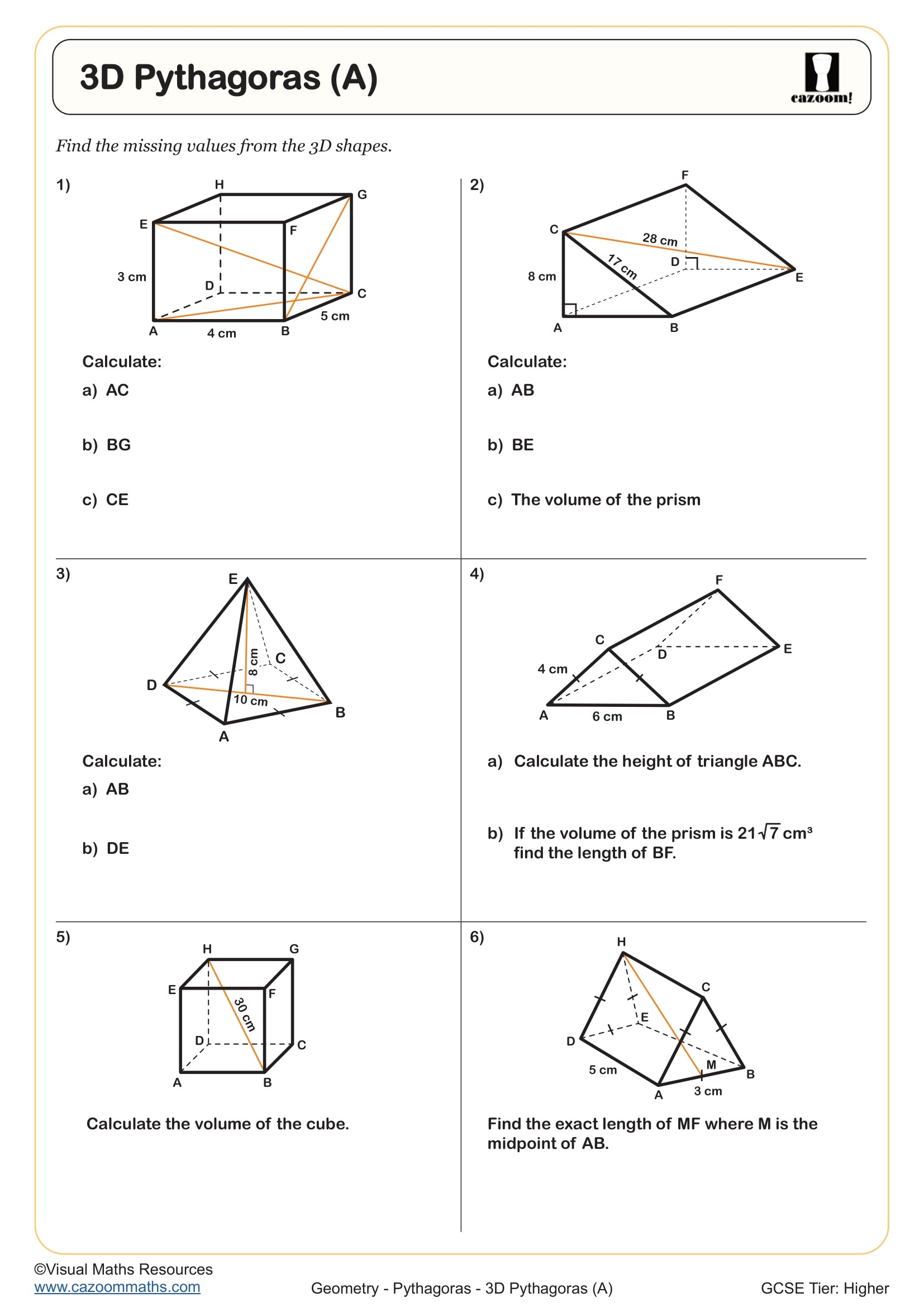
3D Pythagoras (B)

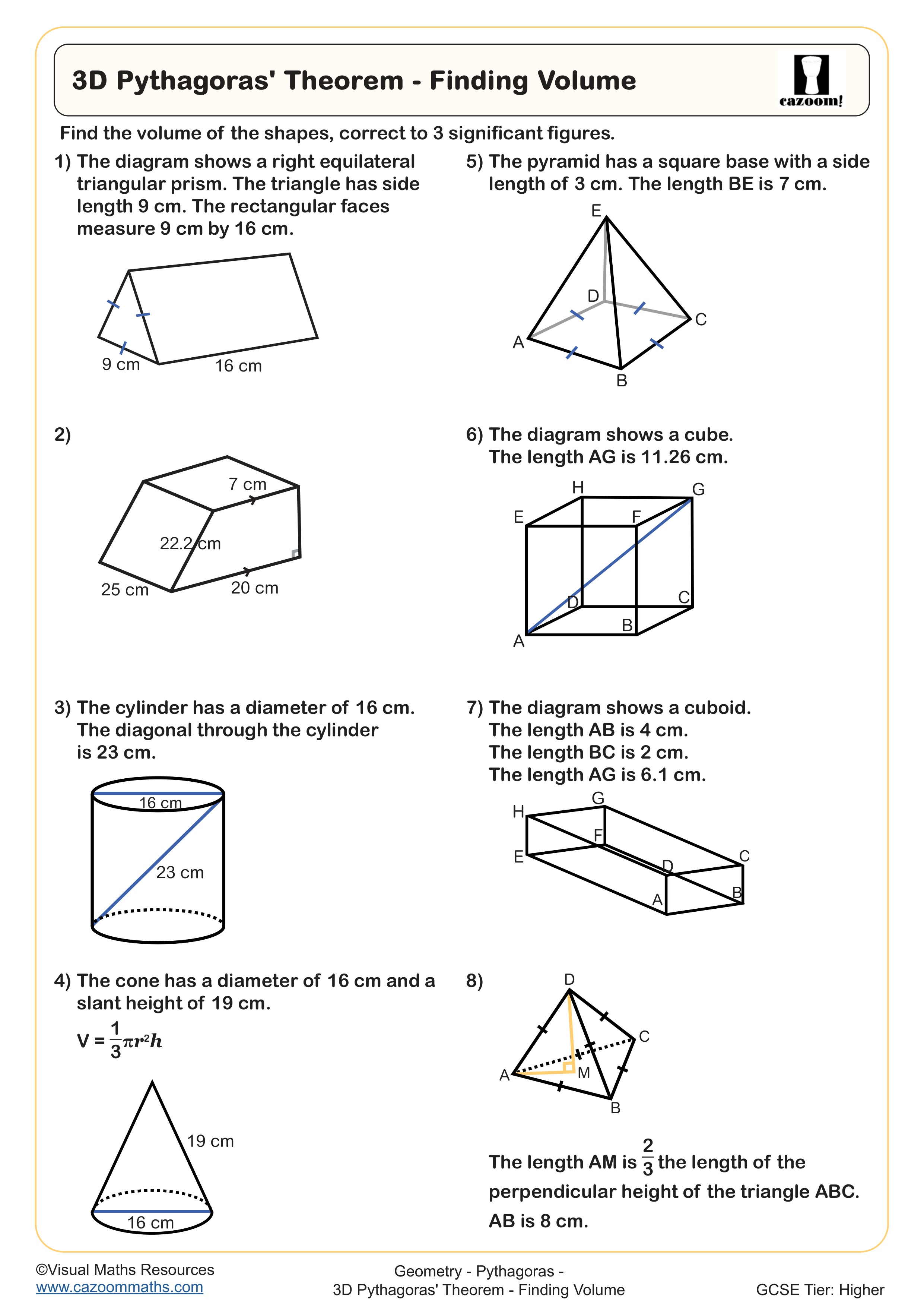
3D Pythagoras' Theorem - Finding Volume
Area of a Triangle Using Pythagoras' Theorem

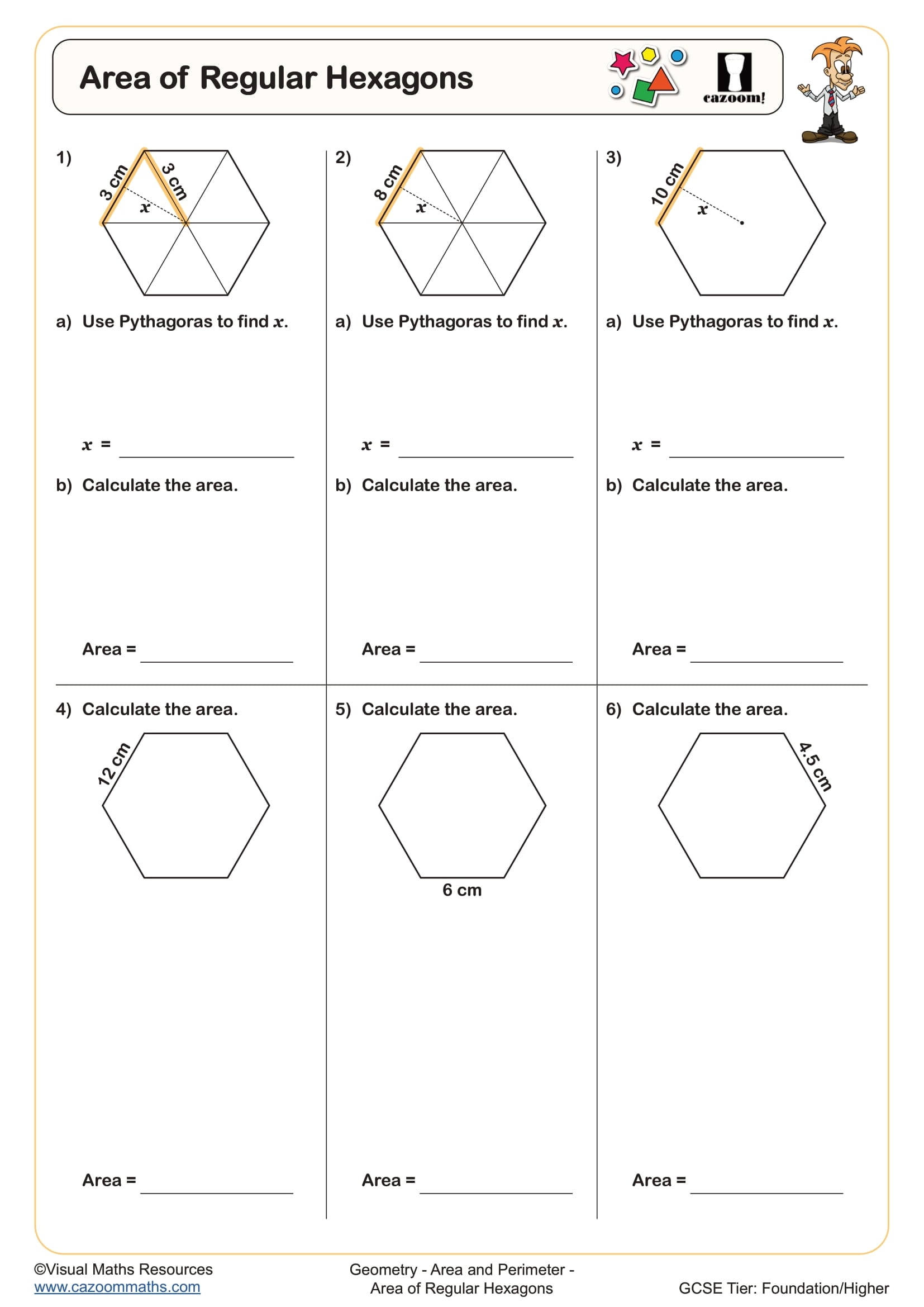
Area of Regular Hexagons
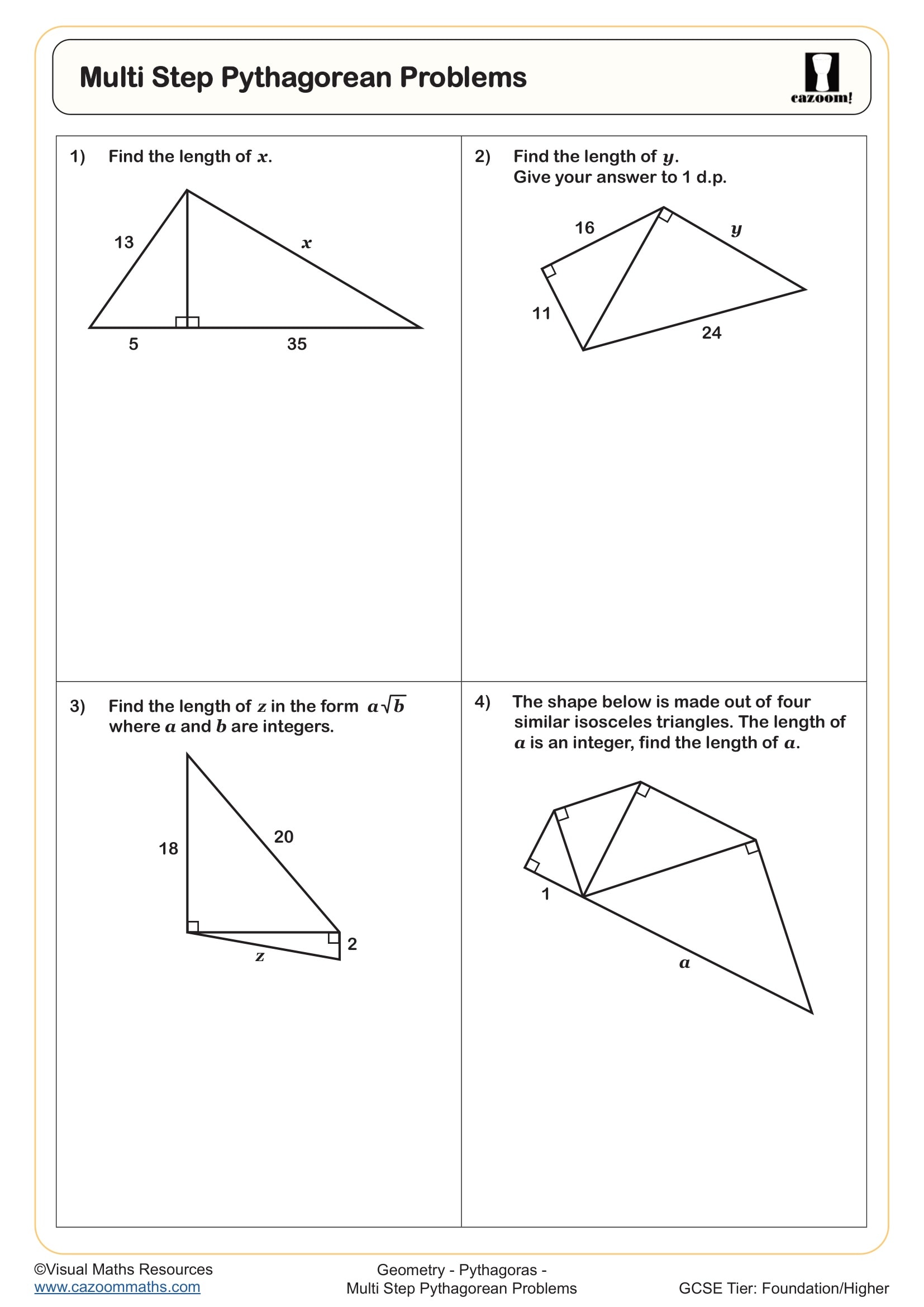
Multi Step Pythagorean Problems
Perimeter Using Pythagoras' Theorem

Pythagoras or Trigonometry? (A)
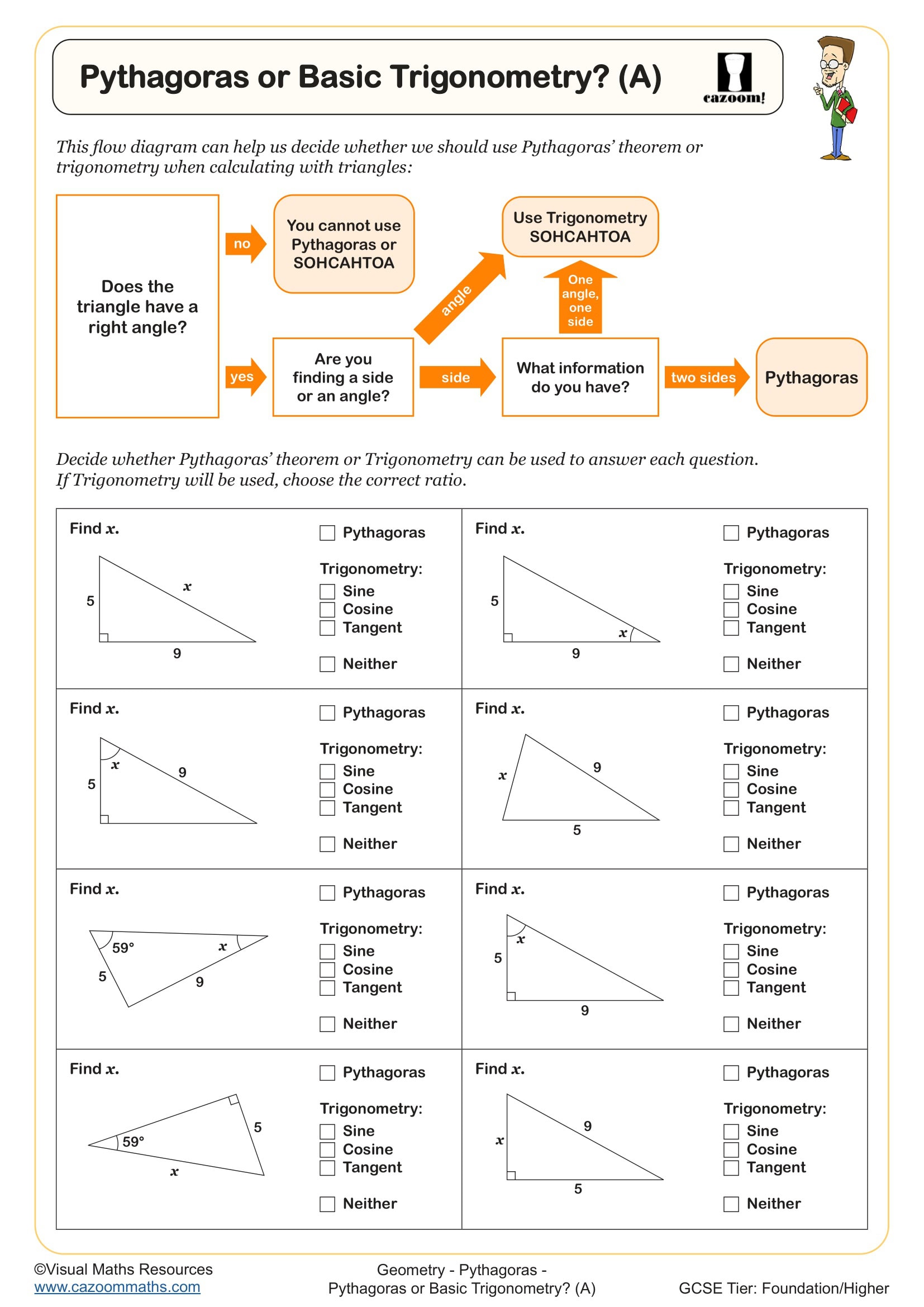
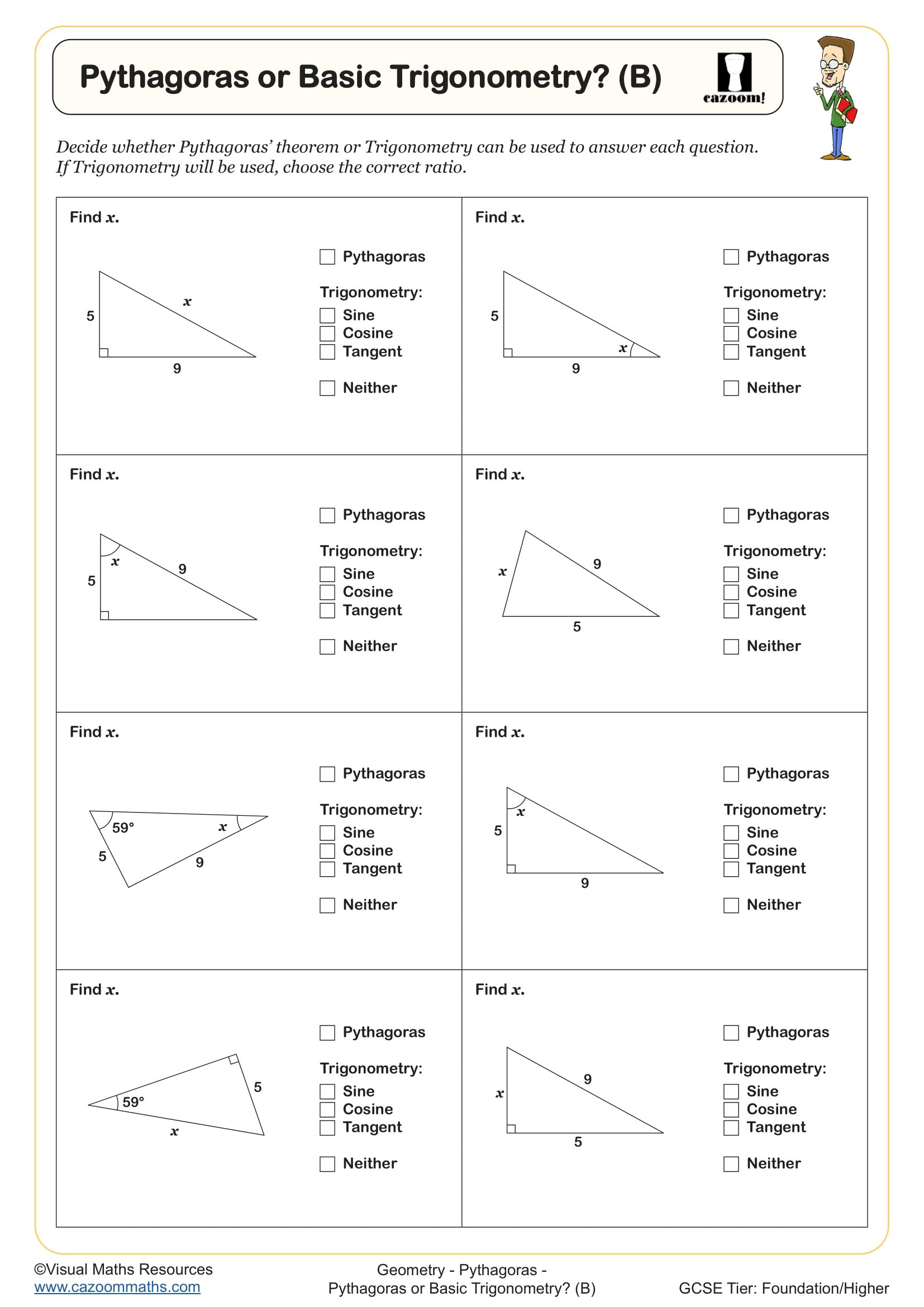
Pythagoras or Trigonometry? (B)
Pythagoras with Surds

Pythagoras Word Problems

Pythagoras Word Problems (With Clues)

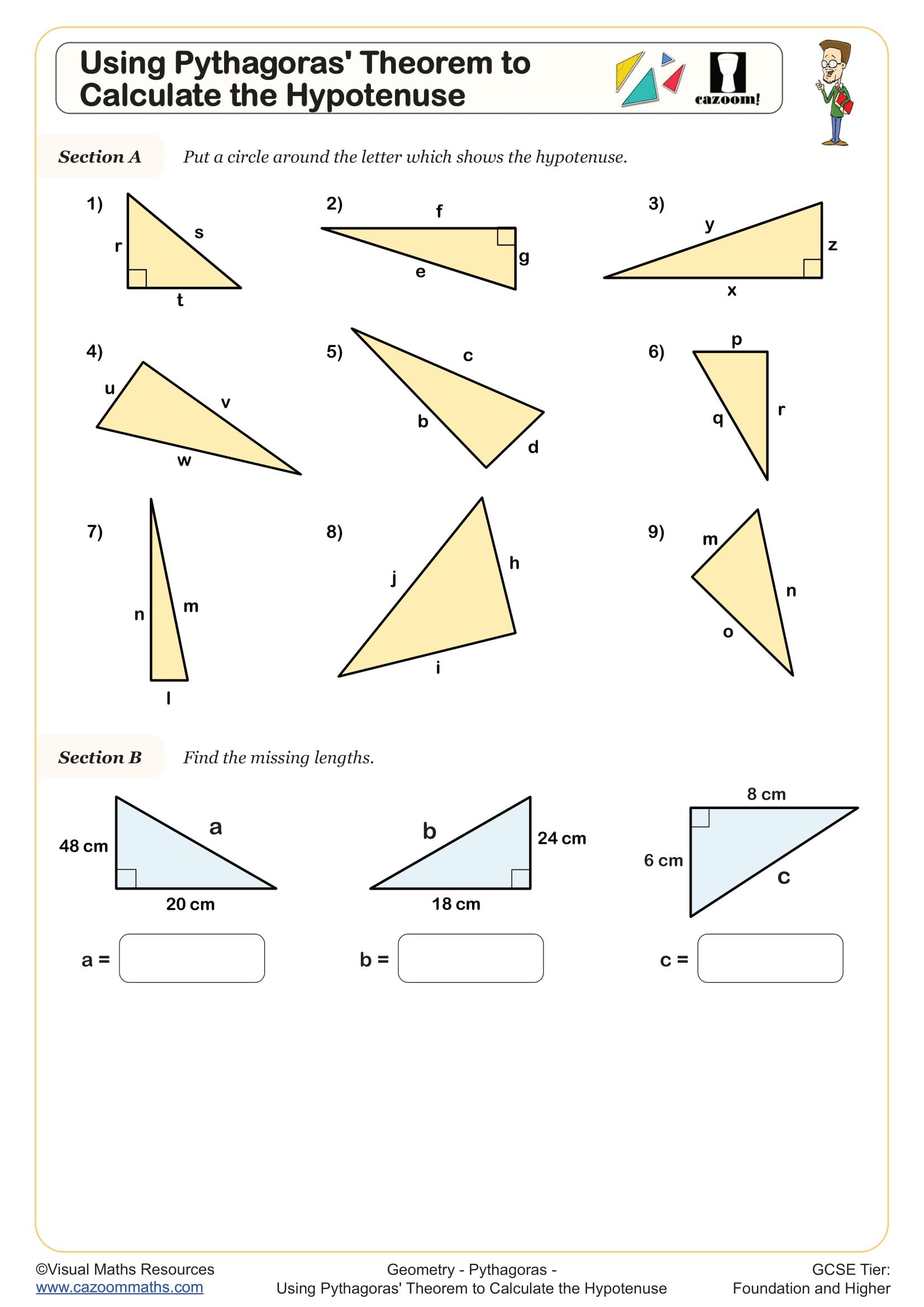
Using Pythagoras Theorem to Calculate the Hypotenuse
Using Pythagoras' Theorem to Calculate Missing Lengths in Right Angled Triangles

Essential Pythagoras Worksheet PDF Downloads That Actually Work
Here's the thing - finding quality Pythagoras theorem worksheets with answers that don't just test memorisation is surprisingly difficult. We've created these worksheets on Pythagoras' theorem resources to show students the thinking process behind each solution. Our detailed answer sheets explain exactly how to identify right-angled triangles, apply the formula correctly, and avoid those common calculation errors that pop up in GCSE papers.
What Skills Are Covered in These Pythagoras Theorem GCSE Worksheets?
We've packed quite a lot into these Pythagoras theorem GCSE questions and answers! Students start with basic a² + b² = c² calculations and progress to more complex multi-step problems. The worksheets include finding missing sides, determining if triangles are right-angled, and applying Pythagoras in coordinate geometry. Students particularly enjoy the problem-solving scenarios (they're actually quite satisfying when you crack them), and the progressive difficulty keeps everyone engaged.
Why Year 11 Students Need Structured Pythagoras Practice Worksheets
Teaching GCSE maths for years, I've noticed that students who master Pythagoras early perform significantly better in their final exams. Regular practice with these Pythagorean theorem worksheets builds that crucial mathematical confidence. These worksheets bridge the gap between understanding the concept and applying it under exam pressure, giving students the repetition they need without the boredom.
• Exam confidence - Students recognise Pythagoras problems instantly
• Calculation accuracy - Reduces silly mistakes with square roots and powers
• Problem-solving skills - Identifies when Pythagoras applies in complex scenarios
• Time management - Faster completion means more time for harder questions
• Grade improvement - Consistent practice typically raises marks by 1-2 grades
Real-World Applications Where Students Actually Use Pythagoras' Skills
Students always ask, "When will I ever use this?" and honestly, Pythagoras appears everywhere once you start looking. In Design Technology, they're calculating material lengths and diagonal measurements. Physics lessons involve resultant forces and vector calculations. Even in Geography, they're working out distances and gradients. It's actually quite satisfying when students suddenly spot Pythagoras in their other subjects and realise they've got the skills to tackle it.
• Construction and carpentry - Ensuring corners are perfectly square
• Navigation and GPS - Calculating shortest distances between points
• Engineering design - Determining structural measurements and supports
• Architecture - Planning staircases, roofs, and diagonal bracing
• Sports analysis - Measuring field dimensions and optimal angles
• Computer graphics - Creating realistic 3D environments and animations