Year 7 Algebra Tiles Worksheets
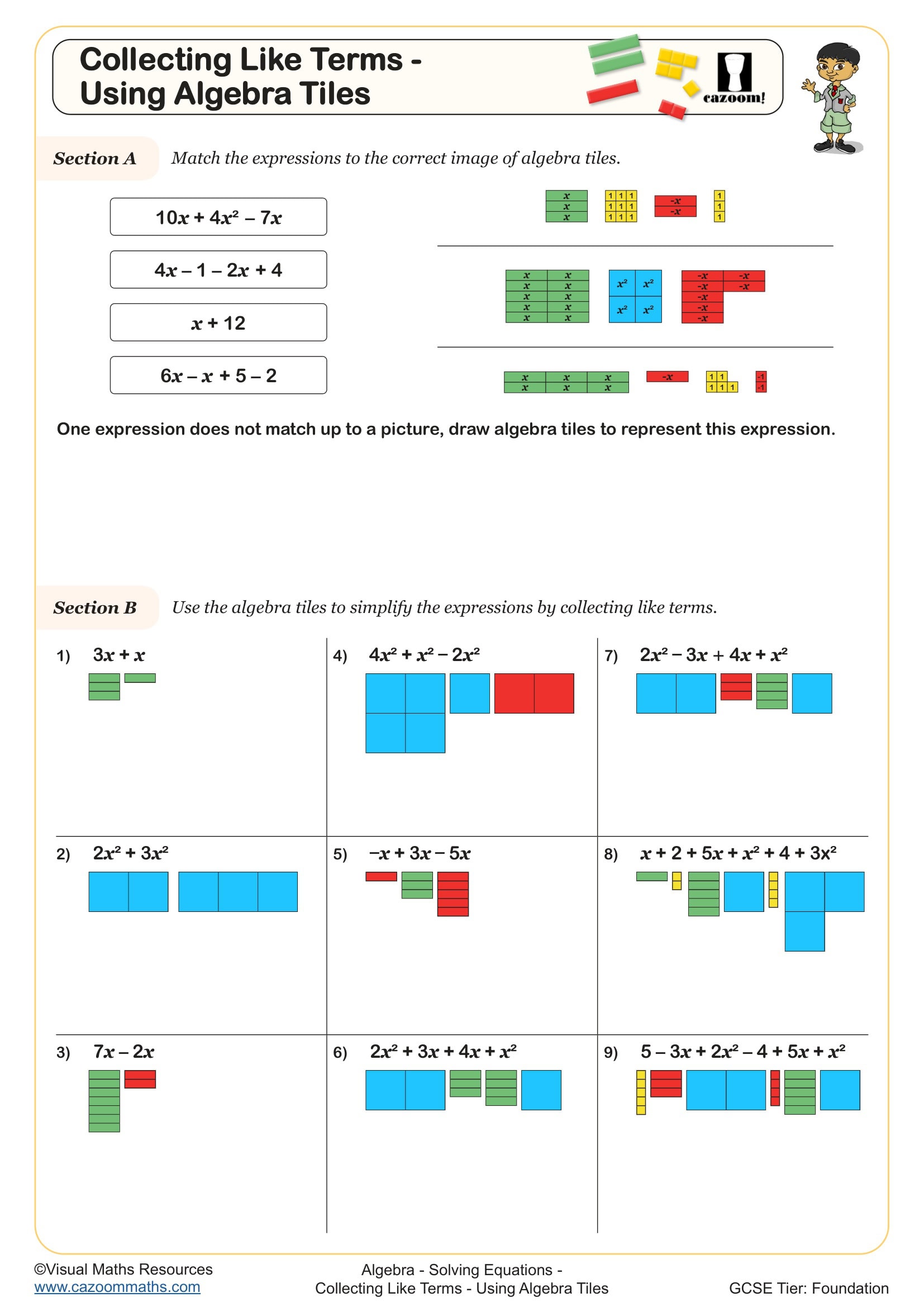
Collecting Like Terms - Using Algebra Tiles
Directed Number - Addition Using Directed Counters

Directed Number - Multiplication Using Directed Number Counters

Directed Number - Subtraction Using Directed Counters

Introducing Algebra Tiles

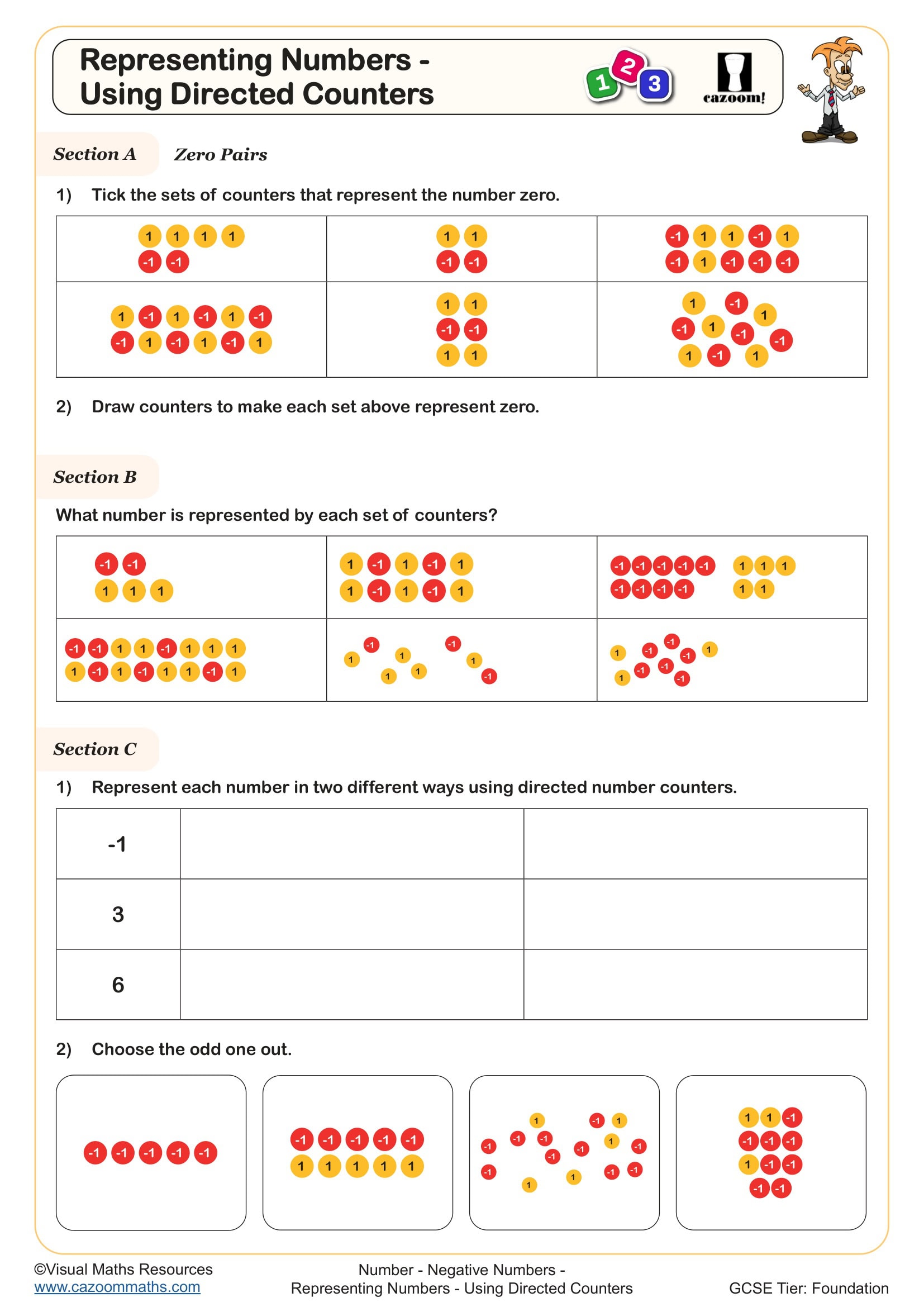
Representing Numbers - Using Directed Counters
Solving One Step Equations with Algebra Tiles

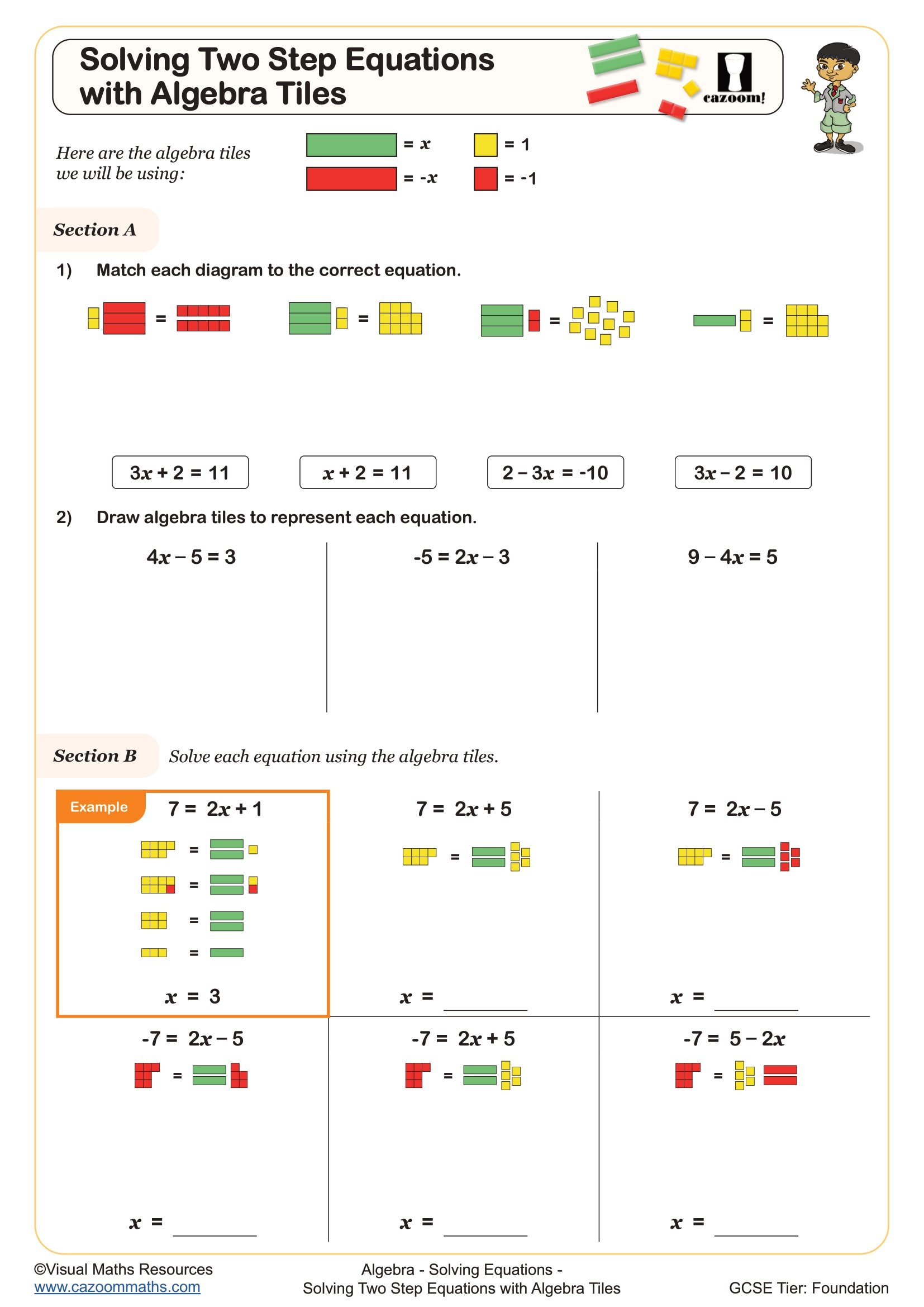
Solving Two Step Equations with Algebra Tiles
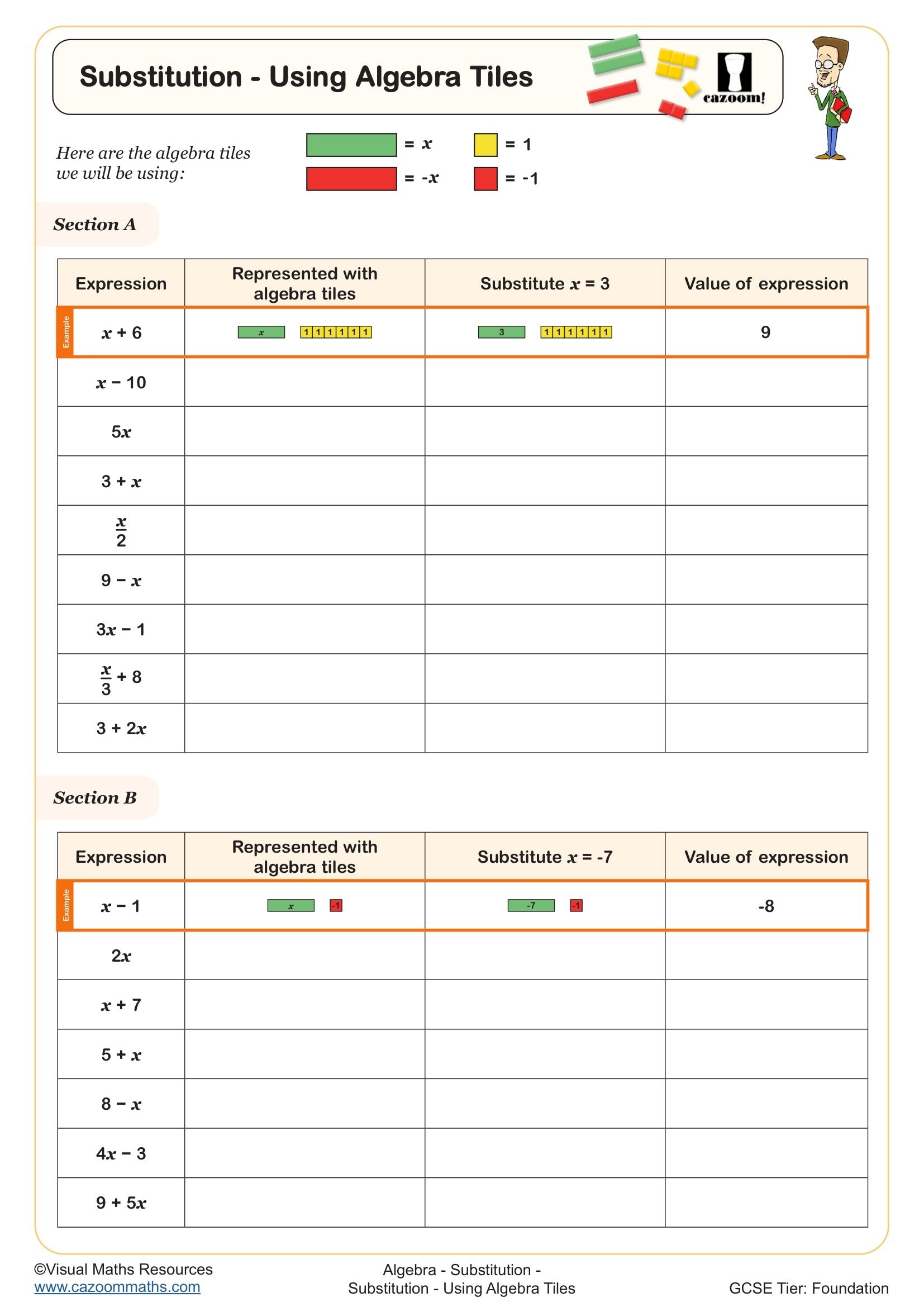
Substitution - Using Algebra Tiles
What are algebra tiles worksheets and how do they help Year 7 students?
Algebra tiles worksheets use rectangular manipulatives to represent variables and constants visually. In the UK curriculum, these appear primarily at KS3 as students transition from numerical work to algebraic thinking. The tiles typically represent x² (large squares), x (rectangles), and units (small squares), allowing students to physically build and manipulate algebraic expressions before working symbolically.
Teachers frequently observe that students who find abstract algebra challenging respond well to the concrete nature of tiles. The physical act of grouping like tiles helps students understand why 3x + 2x = 5x but 3x + 2 cannot be simplified further. However, students sometimes become overly reliant on the tiles and need deliberate practice bridging to symbolic algebra, which is where these algebra tiles worksheets 7th grade pdf resources prove valuable for structured progression.
Which year groups use algebra tiles in the UK curriculum?
Algebra tiles appear primarily in Year 7 within the National Curriculum for England, corresponding to the early stages of KS3. This timing aligns with students' first formal introduction to algebraic notation and manipulation. The visual approach provides scaffolding as students move from the concrete arithmetic of primary school to the abstract reasoning required for GCSE mathematics.
Whilst the concept could extend into Year 8 for students needing additional support, most teachers phase out the tiles as students gain confidence with symbolic manipulation. The progression typically moves from using physical or pictorial tiles to represent expressions, then to simplifying these representations, and finally to working purely with algebraic notation. By the end of Year 7, students should be transitioning away from tiles towards formal algebraic methods that will carry through to GCSE.
How do algebra tiles help students understand simplifying expressions?
Simplifying expressions with algebra tiles involves physically grouping identical tiles together, making the abstract process of 'collecting like terms' tangible. Students place tiles representing an expression like 2x + 3 + x + 5 and then physically group the x-tiles separately from the unit tiles, visually demonstrating why the result is 3x + 8. This concrete manipulation addresses the common error where students incorrectly combine unlike terms.
This skill connects directly to real-world applications in engineering and architecture, where formulae must be simplified before use. For instance, calculating the perimeter of a composite shape produces an expression that needs simplifying, mirroring how architects combine measurements from different building sections. Understanding that only like terms combine translates to understanding that you cannot directly add metres to square metres, reinforcing dimensional analysis crucial in STEM fields.
How can teachers use these algebra tiles worksheets effectively?
The worksheets work best when students initially use physical or digital tiles alongside the printed activities, then gradually progress to completing the worksheets through visualization alone. The answer sheets allow for self-checking, which builds independence and helps students identify exactly where their thinking diverges from correct methods. Teachers report that the structured progression from concrete tile manipulation to pictorial representation to abstract notation mirrors effective teaching sequences for algebraic understanding.
These resources suit various classroom contexts beyond standard lessons. They work particularly well for intervention groups where students need to revisit foundational algebraic concepts with a different approach. Many teachers use them for paired work, where one student builds an expression with tiles whilst their partner writes the symbolic form, then they check against the answer sheet together. The PDF format means they print clearly for homework or can be displayed under visualisers for whole-class discussion of common errors.