Year 8 Algebra Tiles Worksheets
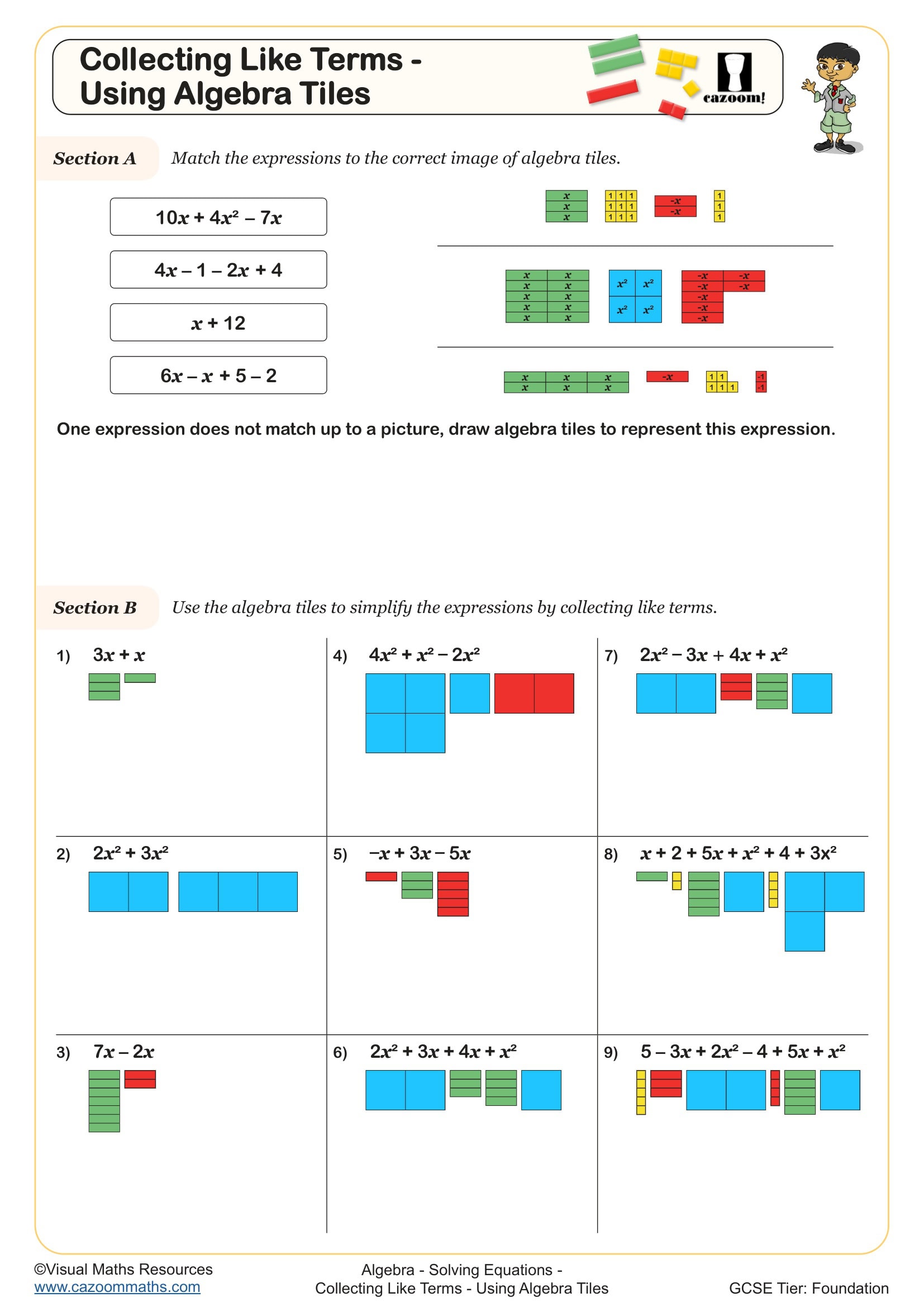
Collecting Like Terms - Using Algebra Tiles
Directed Number - Addition Using Directed Counters

Directed Number - Multiplication Using Directed Number Counters

Directed Number - Subtraction Using Directed Counters

Expanding Brackets and Simplifying - Using Algebra Tiles

Expanding Double Brackets (A) Using the Grid Method

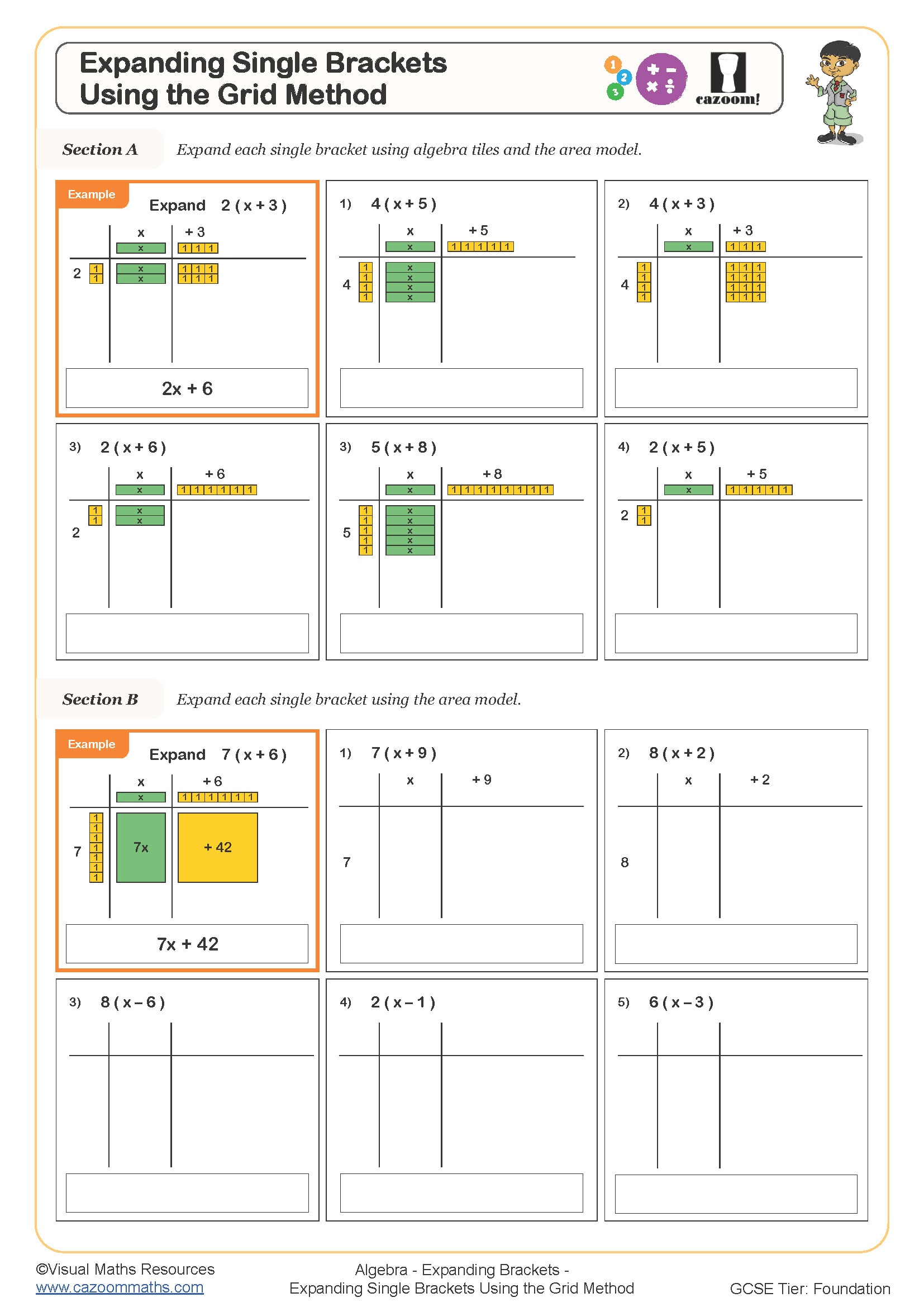
Expanding Single Brackets - Using the Grid Method
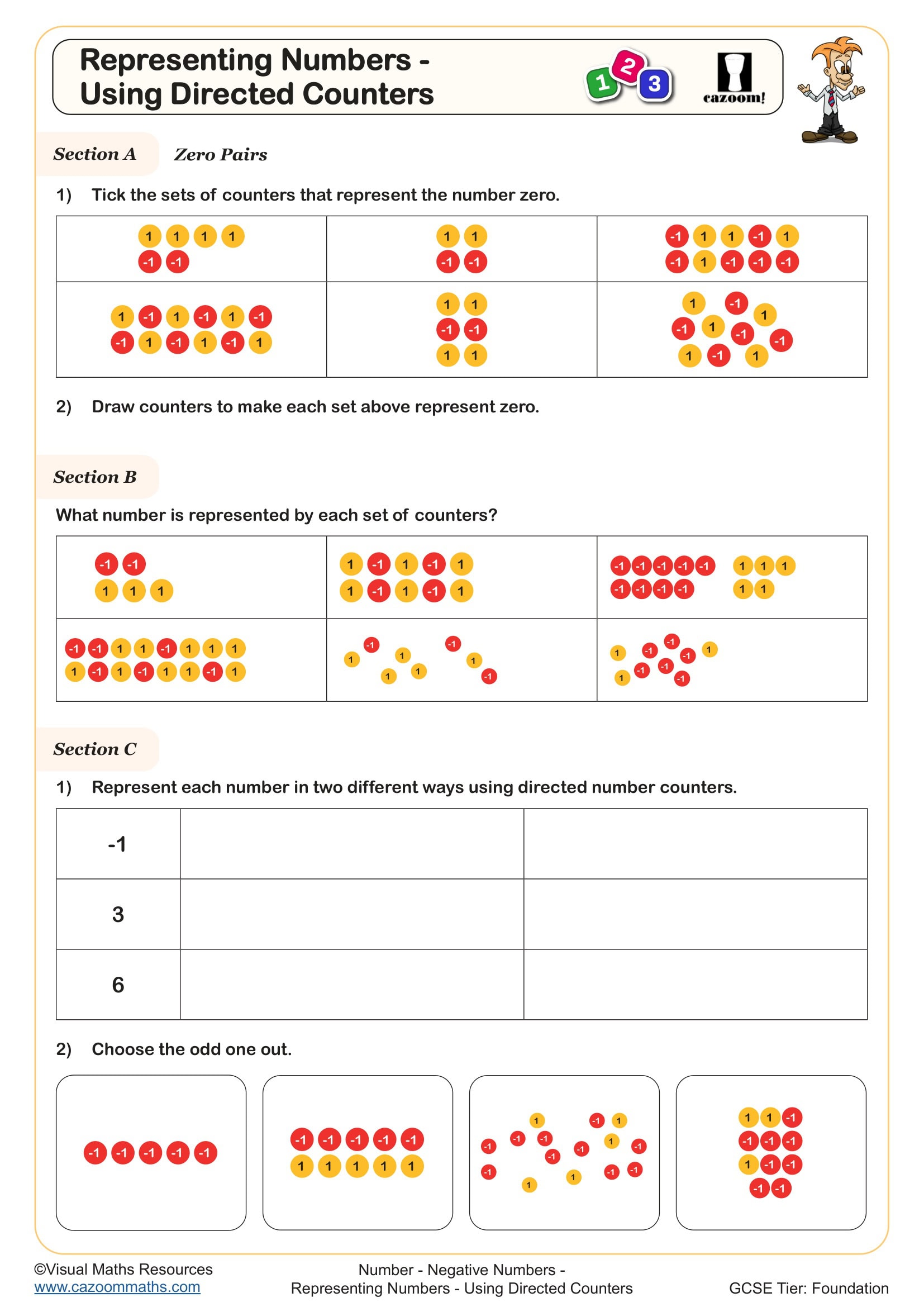
Representing Numbers - Using Directed Counters
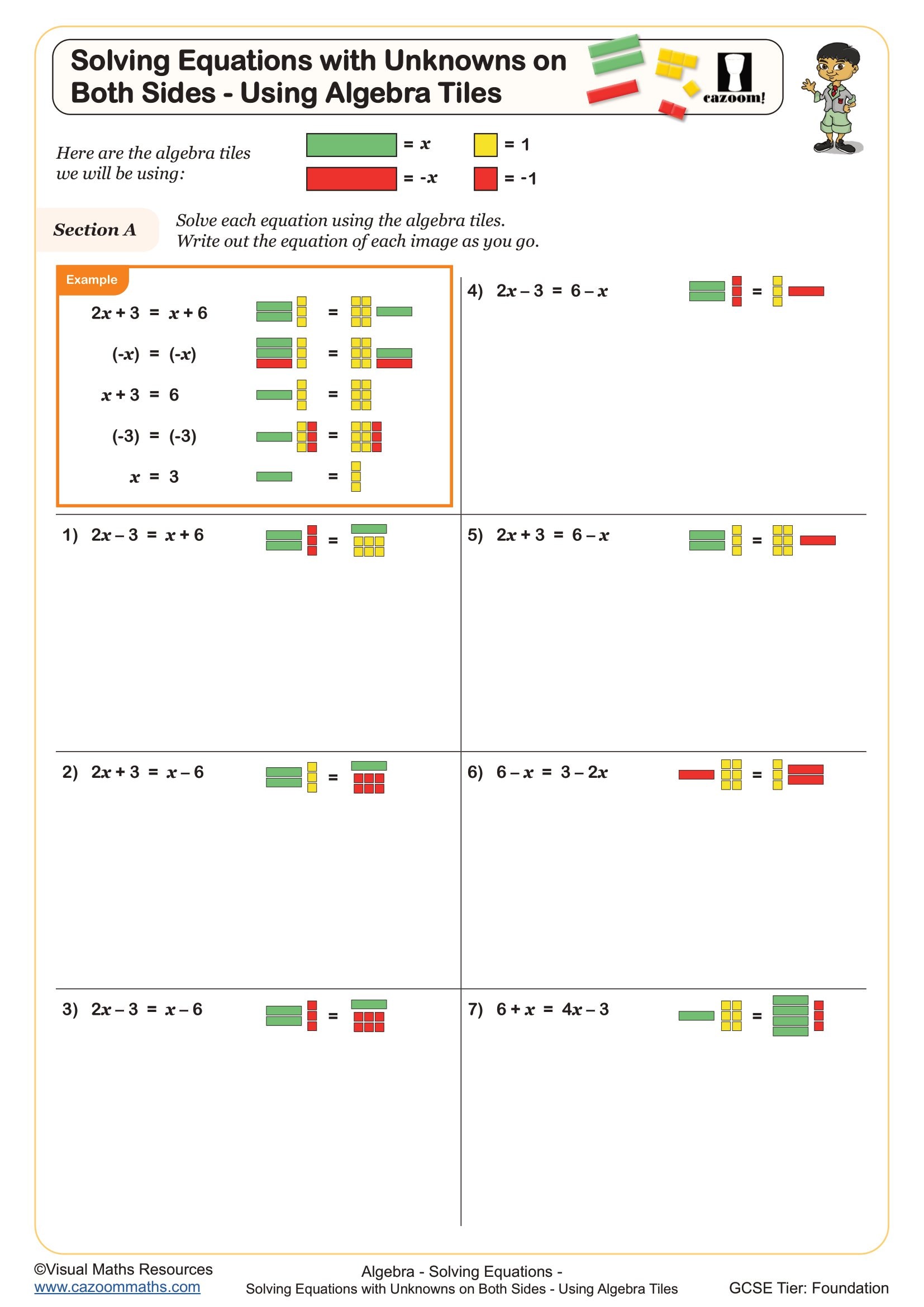
Solving Equations with Unknowns on Both Sides - Using Algebra Tiles
Solving One Step Equations with Algebra Tiles

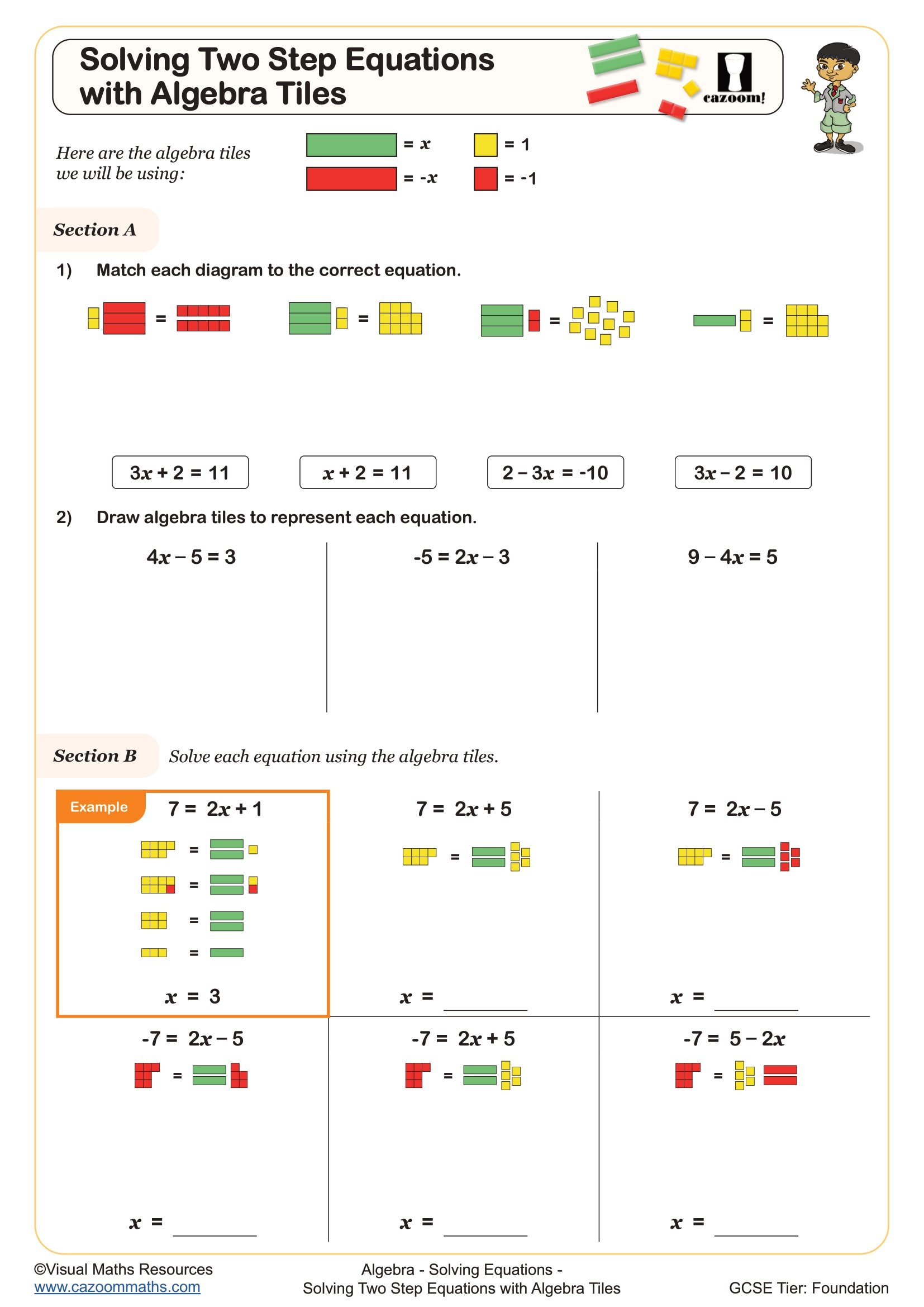
Solving Two Step Equations with Algebra Tiles
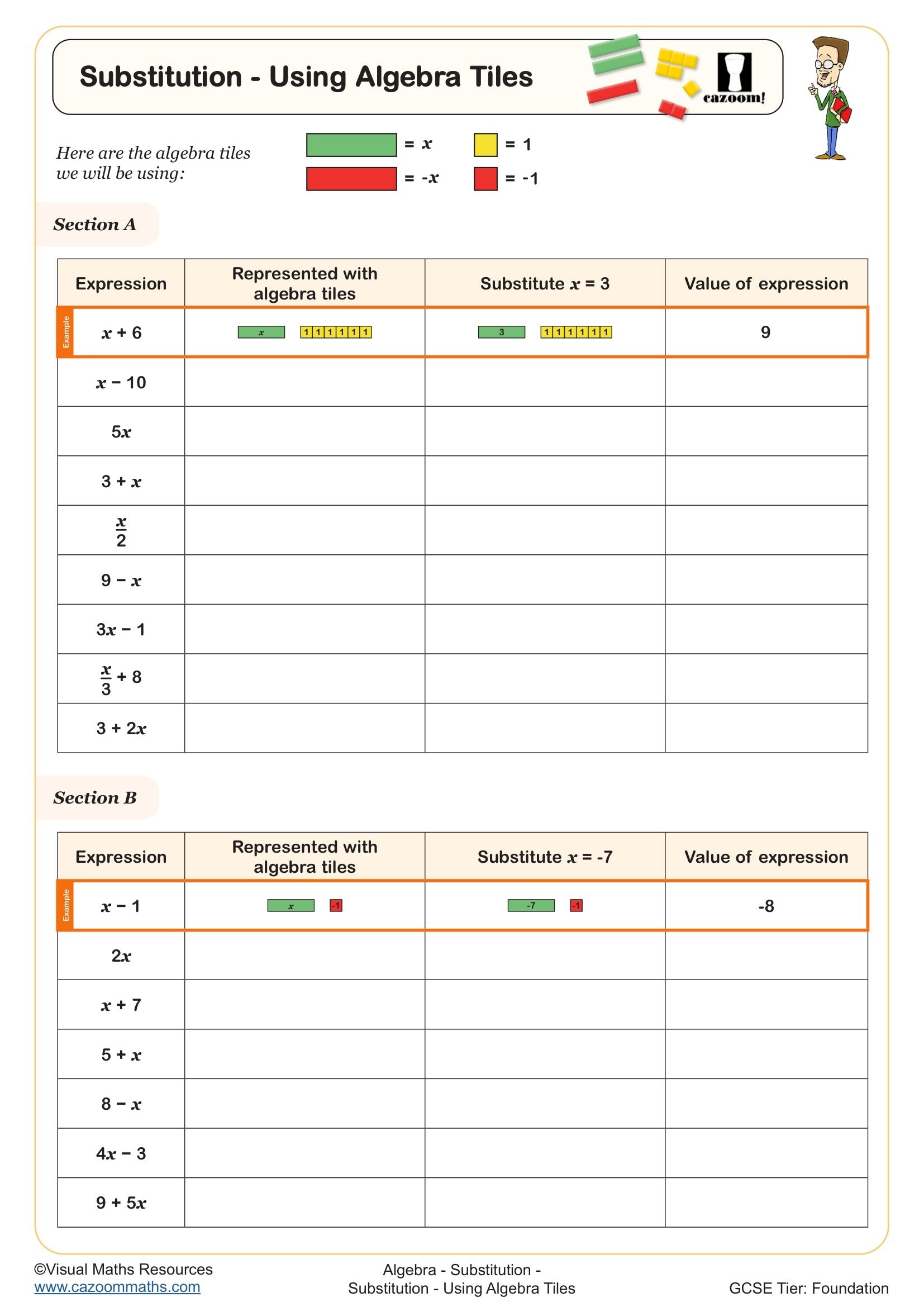
Substitution - Using Algebra Tiles
What are algebra tiles and how do they help students learn algebra?
Algebra tiles are rectangular manipulatives that represent variables and constants in algebraic expressions. A long thin rectangle typically represents x, a small square represents 1, and a large square represents x². Different colours or shading distinguish positive from negative values, allowing students to physically model expressions like 3x + 5 or 2x² - 4x + 3.
The visual and tactile nature of algebra tiles helps students understand why like terms combine and unlike terms don't. Teachers frequently observe that students who model equations with tiles first develop stronger conceptual understanding than those who jump straight to symbolic manipulation. A common error occurs when students forget that removing tiles requires adding zero pairs (one positive and one negative tile that cancel), particularly when solving equations that need terms moved across the equals sign.
Which year groups use algebra tiles in the UK curriculum?
Algebra tiles appear primarily in Year 8 as part of the Key Stage 3 National Curriculum, when students transition from basic algebraic notation to more complex manipulation of expressions and equations. At this stage, the curriculum expects students to understand abstract algebraic concepts, and tiles provide scaffolding for those finding the jump from concrete arithmetic challenging.
Whilst some Year 7 classes introduce algebra tiles when first encountering algebraic notation, and occasional Year 9 intervention groups use them for revision, Year 8 represents the core teaching point. The worksheets build from representing simple expressions through collecting like terms, expanding brackets, and ultimately solving equations. By the end of Year 8, most students move beyond needing the physical representation, though the mental model of tiles often remains useful throughout GCSE.
How do algebra tiles help when solving equations with unknowns on both sides?
When solving equations like 3x + 2 = x + 8, students arrange tiles on both sides of a physical or drawn equals sign, then systematically remove identical tiles from each side until the unknown is isolated. This process makes the concept of balancing equations visible rather than procedural. Students physically see that subtracting x from both sides means removing one x-tile from each side, maintaining equality.
This understanding connects directly to computer programming and engineering contexts where equations model real systems. In control systems, engineers balance input and output equations to maintain stability, using precisely the same algebraic principles. Students learning to solve equations with tiles develop the logical thinking required for debugging code or balancing chemical equations in science, where maintaining equality whilst manipulating both sides is fundamental. The tile model provides the conceptual foundation for these applications.
How can teachers use these algebra tiles worksheets effectively in lessons?
The worksheets work alongside physical or virtual algebra tiles, allowing students to record their tile arrangements and then write the equivalent algebraic expressions. Each worksheet typically shows tile diagrams that students must interpret, then progresses to problems where students create their own tile representations. The answer sheets include both visual tile solutions and algebraic working, helping teachers quickly identify whether errors are conceptual or procedural.
Many teachers use these worksheets during initial teaching as guided practice, with students working through examples whilst manipulating physical tiles at their desks. They're equally valuable for intervention work with Year 9 students struggling with algebraic manipulation before GCSE, providing a concrete method to revisit foundational concepts. Paired work proves particularly effective, with one student arranging tiles whilst the other writes the algebra, then swapping roles, encouraging mathematical discussion about why certain operations work.